基于Stewart平臺的光電吊艙隔振系統設計

方新文

（中國飛機強度研究所，西安 710065）

光電吊艙是光電偵察裝備中的重要組件，也是機載偵察設備的核心部分，廣泛應用于陸地、海洋、空中以及空間的偵察。光電吊艙在工作時會受到飛行器速度姿態變化以及發動機振動的影響，振動不僅影響到吊艙設備的使用壽命，還使得吊艙的成像質量嚴重下降。因此對光電吊艙的振動控制必不可少。光電吊艙的隔振系統的實現方法很多，例如加裝不同類型的隔振器或者設計特殊的無轉角隔振平臺[1]。Stewart平臺作為光電吊艙的隔振系統也是一種適宜的實現方法。

Stewart 平臺機構是1965 年由美國學者Stewart首次提出并將其作為一種飛行模擬器[2]。平臺具有大剛度、高精度和高載荷自重比的特點，適用于高精度、大載荷且對工作空間要求相對較小的場合。目前已經在航空、航天、地下開采、制造裝配等行業有著較為廣泛的應用。針對Stewart 平臺的理論模型與動態力學行為，已有了不少研究。

楊劍鋒等[3]設計了一種Stewart平臺隔振系統用于某型空間光學載荷的在軌隔振，研究了系統的性能特點，得到了用于六維被動隔振的最佳構型。Lu等[4]研究了一種高靜剛度、低動剛度的Stewart平臺，實現了6 自由度方向振動的降低；同時基于剛體動力學和非線性彈性理論得到了1階主振的傳遞率和功率輸出的頻響函數。Zheng 等[5]也建立了一種帶有Stewart平臺的隔振系統，研究了支撐桿的剛度特性，建立了包括幾何非線性和剛度非線性在內的非線性動力學模型，并評估了非線性對隔振性能的影響。Wu 等[6]則研究了一種Stewart 平臺的理論模型并進行了試驗驗證，以6 個X 形結構的支撐桿實現了6 個方向的良好性能可調節的隔振系統。Yun等[7]、Yi等[8]、沈慧平等[9]也都基于工程實際設計了不同的Stewart平臺并研究了其動態力學性能，取得了不同程度的進展，但是針對被動Stewart隔振平臺的解耦隔振設計方法以及等剛度設計方法還少有研究[10－22]。

本文通過建立Stewart平臺的理論數學模型，研究被動Stewart 平臺隔振系統的解耦設計以及等剛度設計方法。通過有限元仿真以及虛擬試驗對設計方法進行驗證與分析對比。

1 Stewart平臺理論分析

1.1 數學模型的建立及分析

典型的Stewart平臺由上安裝平臺、下安裝平臺以及平臺之間的阻尼連桿組成。平臺與阻尼連桿之間采用柔性鉸接，可以相互有限度地自由活動。整個系統通過阻尼連桿的伸縮與變形達到振動隔離的目的。圖1 所示為Stewart 平臺的數學模型，在上安裝平臺與設備組成的整體的質心處建立Oxyz笛卡爾坐標系。

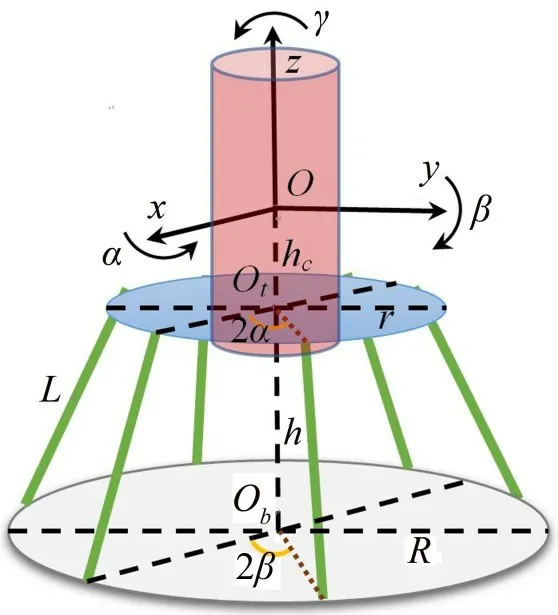
圖1 Stewart平臺數學模型

圖1 中：上安裝平臺的直徑為r；下安裝平臺的直徑為R；上安裝平臺的圓心為Ot，下安裝平臺的圓心為Ob；兩個平臺之間的高度為h；平臺之間通過6根支撐桿連接，支撐桿的長度為L；支撐桿連接點與上安裝平臺之間的夾角為2α；支撐桿連接點與下安裝平臺之間的夾角為2β；O點與Ot點之間的距離為hc。由以上參數即可以建立起一個Stewart平臺。

在微幅振動的條件下，含有基礎位移激勵的Stewart平臺的動力學方程如式（1）所示[23]：

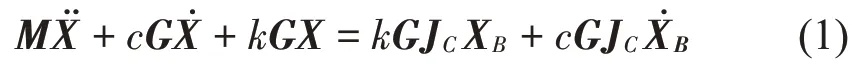
式中：M為上安裝平臺的質量矩陣；G為Stewart平臺的系統構型矩陣，G=JTJ，J為系統Jacobian矩陣；X為上安裝平臺的位移矩陣；JC為下安裝平臺到上安裝平臺的Jacobian 運動傳遞矩陣；XB為基礎位移激勵矩陣；c為支撐桿的阻尼；k為支撐桿的剛度。

上安裝平臺的質量矩陣M，如式(2)所示：

式中：m為包括載荷在內的上安裝平臺的總質量；I是其慣性張量矩陣，且I=Diag[Ix Iy Iz]。

上安裝平臺的位移矩陣X，如式(3)所示：

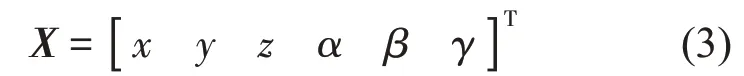
基礎位移激勵矩陣XXB如式(4)所示：

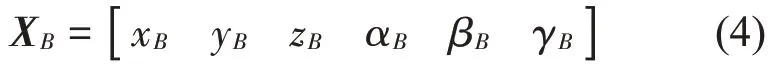
Stewart平臺的Jacobian矩陣J如式(5)所示：

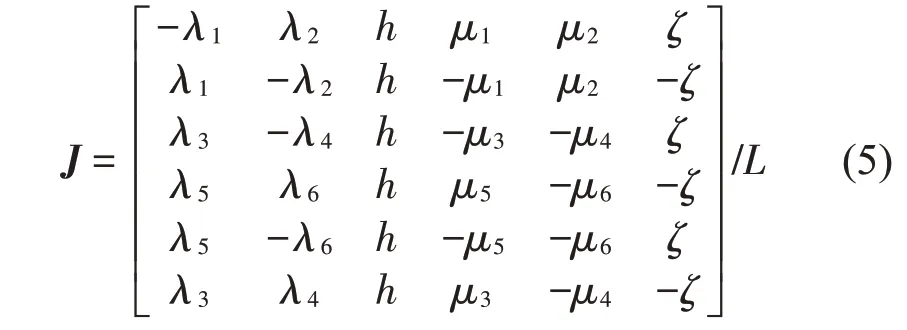
式中：L為支撐桿的長度，且有：

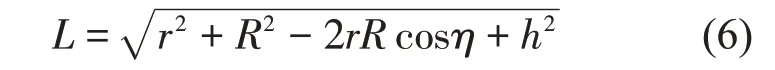
矩陣中其余的參數分別為：

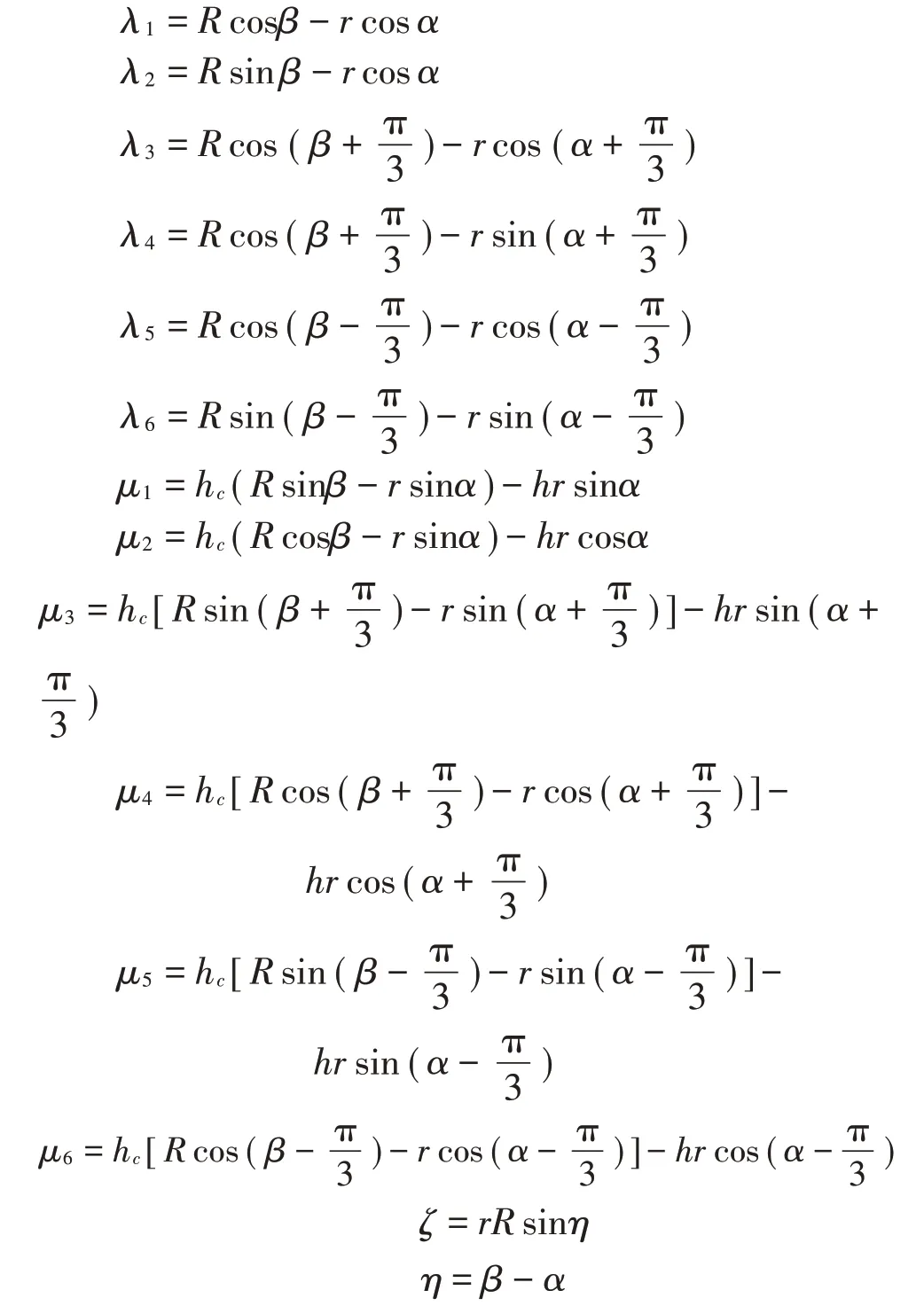
下安裝平臺到上安裝平臺的Jacobian運動傳遞矩陣JC如式(7)所示：

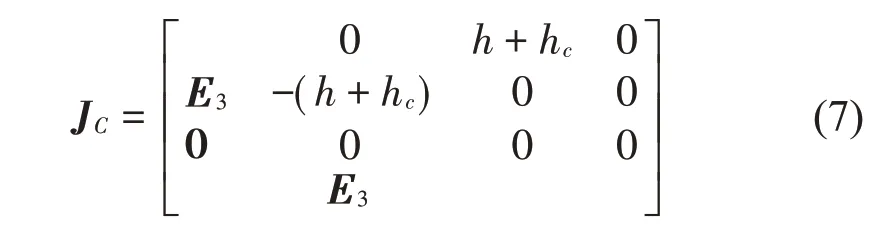
根據系統的Jacobian矩陣J，可以計算得其構型矩陣G矩陣如式(8)所示：

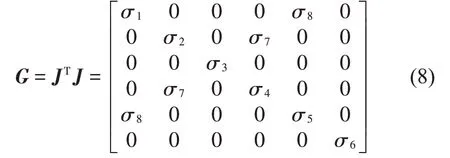
式中各項參數分別為：

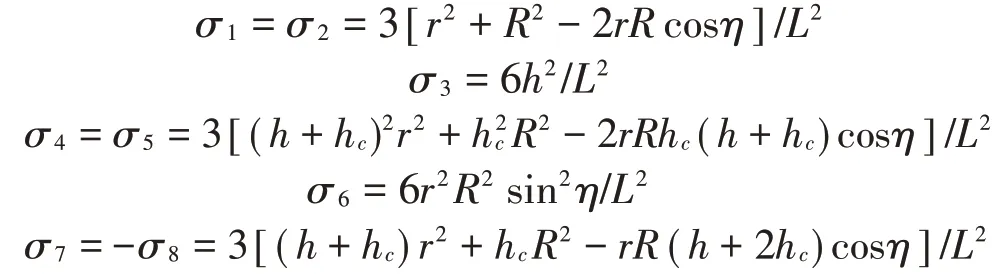
容易看出Stewart平臺的動力學方程中，x與β耦合，y與α耦合，z與γ均獨立。因此可以將矩陣方程進行分解，得到4個相互獨立的動力學方程。

計算得x-β方向耦合動力學方程如式(9)所示；yα方向耦合動力學方程如式(10)所示；z方向動力學方程如式(11)所示；γ方向動力學方程如式(12)所示：

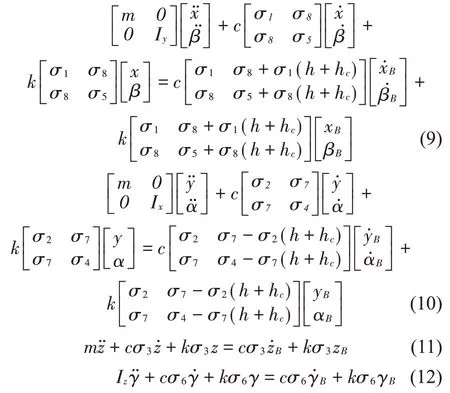
1.2 等剛度解耦設計分析

先考慮一種最簡單的情況，即當上下安裝平臺半徑相同，負載的質心位于上下安裝平臺正中心，并且支撐桿的張角為90°(π/2)時Stewart平臺的動力學響應。此時有：

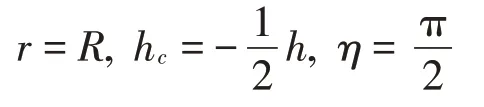
易計算得σ7=σ8=0，在這種安裝情況下Stewart平臺不會發生耦合振動，各個方向的動力學方程均相互獨立。事實上這種結構即為Geng 設計的立方體Stewart 平臺[24－26]，其特點是所有支撐桿兩兩相互垂直，設備質心安裝于平臺的幾何中心處。由此可以保證所有方向完全解耦。當然對于立方體Stewart平臺而言，因為必須保證設備的質心在幾何中心并且支撐桿兩兩垂直才能解耦，不僅安裝難度較高，占用空間也很大，在很多場合中都難以應用。因此在實際工程應用中還需要考慮其他情況時Stewart 平臺的動力學狀態分析。

從式(9)及式(10)的耦合方程分析中可以得出：倘若要使平臺不發生耦合振動，即各個方向的動力學方程完全解耦，則需要滿足：

計算式(9)可以得到系統分別沿x與β方向的模態頻率如式(14)所示；計算式(10)可以得到系統分別沿y與α方向的模態頻率如式(15)所示：

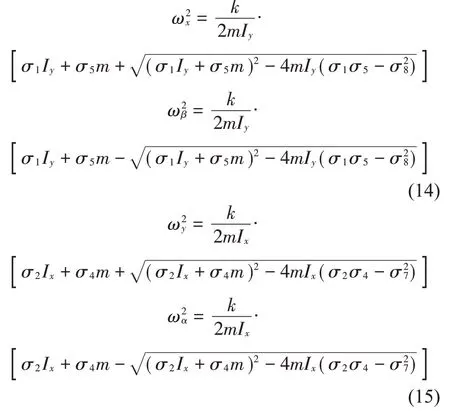
計算式(11)得到沿z方向的模態頻率為：

計算式(12)得到沿γ方向的模態頻率為：

從計算結果可以看出如果要實現x向與y向等剛度，即x向與y向模態頻率相同，則應保證：Ix=Iy，即平臺及設備都應該關于z軸對稱。由前述分析，為了保證平臺不發生耦合振動，應保證σ7=σ8=0，同時為了實現平臺在x向與z向等剛度，令ωx=ωz。代入式(14)與式(16)中，則有：

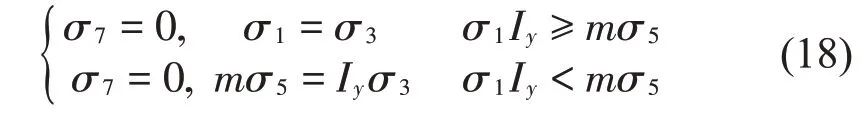
計算式(18)可得：

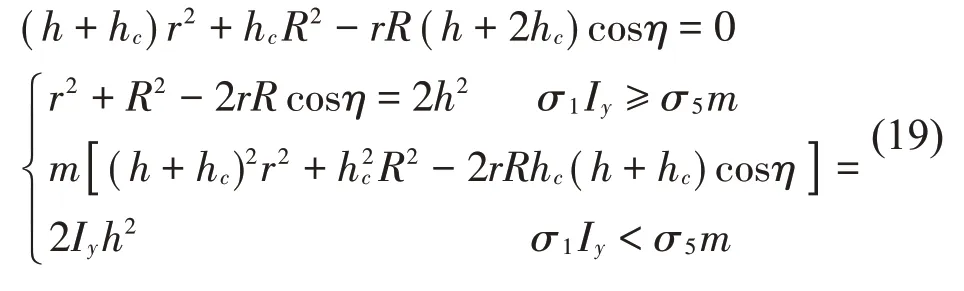
由此得到了各個方向解耦且三向等剛度的Stewart平臺設計準則，即在設計時應使Stewart平臺的結構參數滿足式(19)。

2 Stewart平臺設計分析

2.1 隔振系統參數設計

以某型光電吊艙為例研究Stewart 平臺參數對整個隔振系統性能的影響。吊艙的質量為9.37 kg，其慣性特性如表1所示。

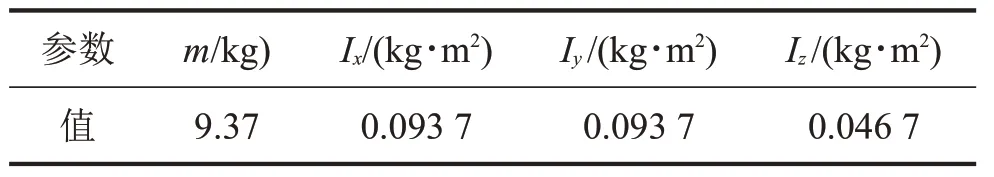
表1 某型光電吊艙慣性參數

在設計Stewart平臺時，一般平臺的最大安裝直徑2R以及安裝高度h會因為工程要求受到限制。此吊艙要求最大安裝直徑不超過0.5 m，安裝高度不大于0.1 m，設計R=0.24 m，h=0.1 m。同時設計上下平臺的支撐桿安裝角度分別為20°與50°。

將這些值代入式(19)中，通過計算可以得到Stewart平臺的各項設計參數如表2所示。

表2 Stewart平臺設計參數

2.2 隔振系統模態分析

依據計算所得設計參數建立光電吊艙隔振系統有限元分析模型，如圖2所示。

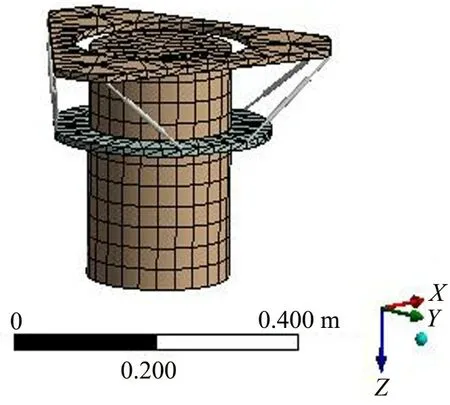
圖2 隔振系統有限元分析模型

分別根據式(14)至式(17)計算隔振系統的各個方向的模態頻率，并與有限元仿真分析結果進行對比，結果如表3所示。前6階有限元仿真結果如圖3所示。

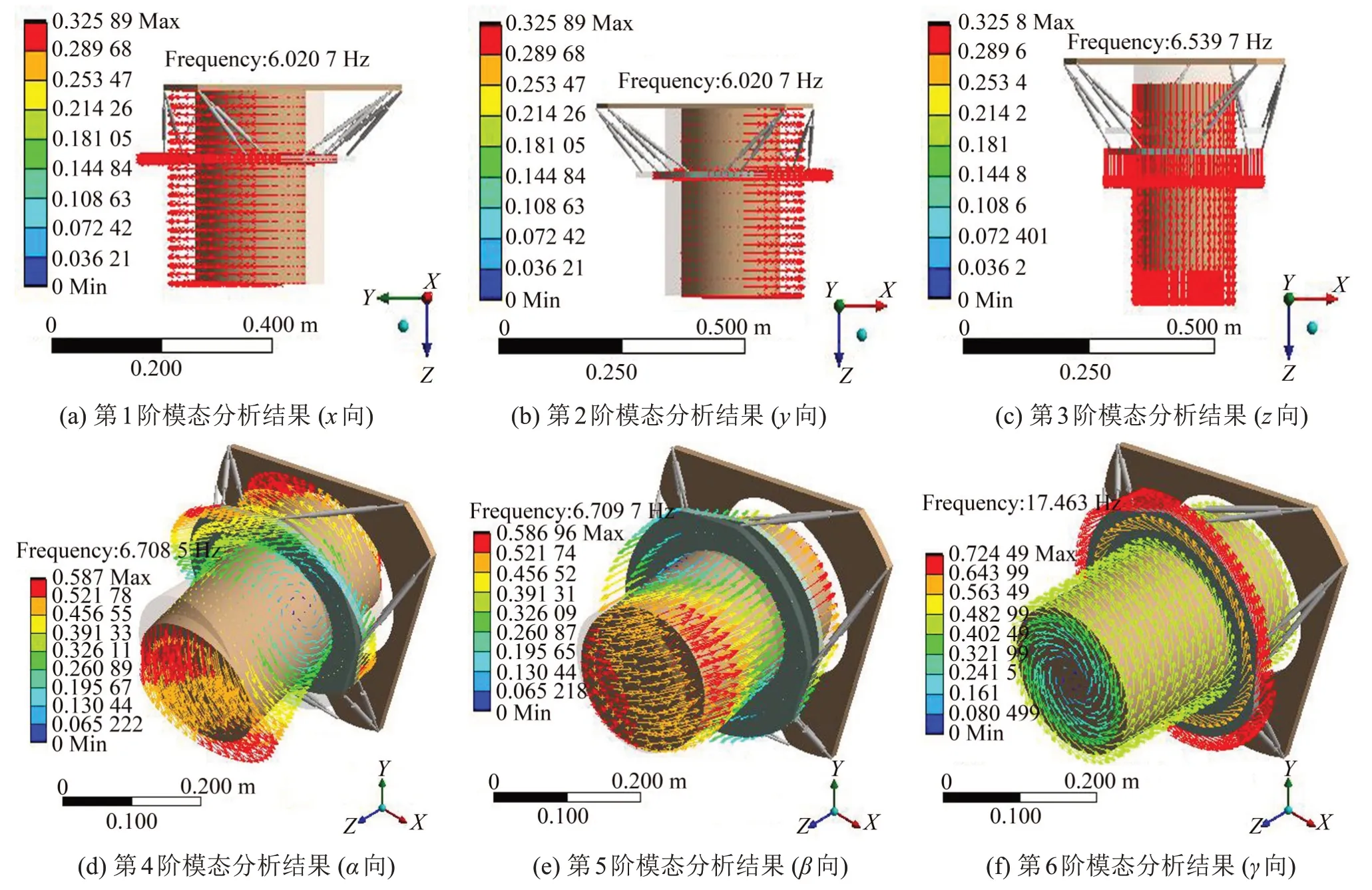
圖3 隔振系統有限元分析結果

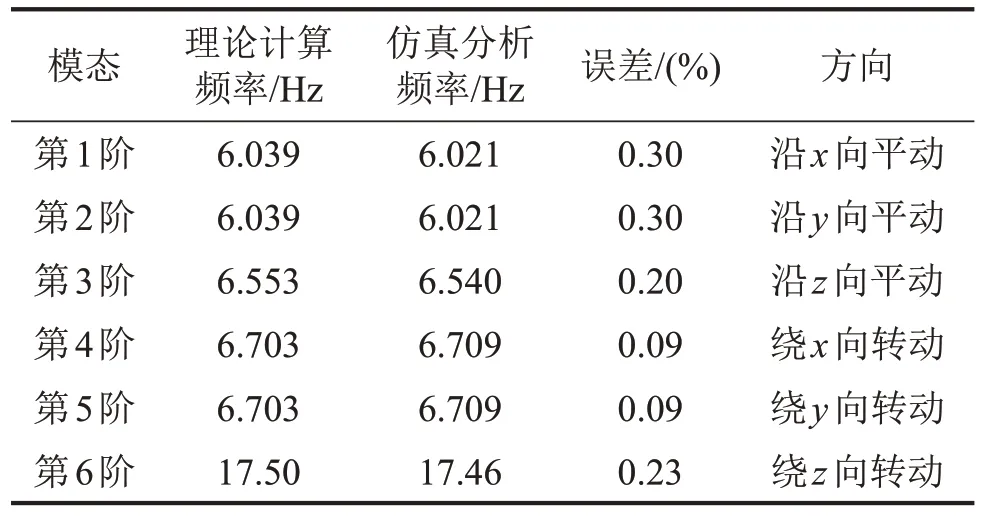
表3 隔振系統設計結果

結果顯示理論計算所得模態頻率與有限元仿真結果相吻合，二者之間最大誤差不超過0.30%.有限元結果顯示隔振系統在前6 階振動均相互獨立，沒有發生線振動與角振動的耦合現象。同時隔振系統前3 階模態頻率基本一致，實現了三向等剛度設計要求，三軸向的模態頻率差別不大于7.8%。

2.3 隔振系統的傳遞函數分析

在有限元模型的軸向(z)與徑向(x、y)分別施加正弦激勵，分析隔振系統在各個方向上的傳遞函數。計算結果如圖4所示。

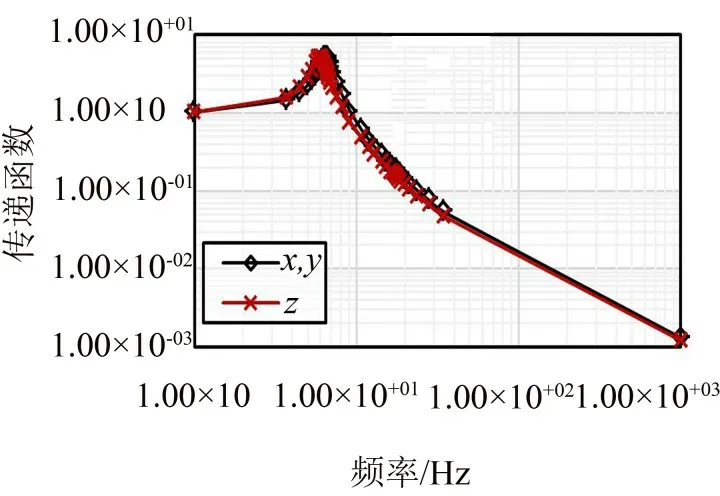
圖4 隔振系統傳遞函數曲線

有限元分析結果顯示：隔振系統沿著軸向(z)與徑向(x、y)的共振頻率接近，基本實現等剛度設計。徑向(x、y)已實現解耦設計，傳遞函數沒有角振動(β、α)帶來的2階響應。

3 Simulink仿真分析及驗證

3.1 光電吊艙質心對隔振系統的影響

光電吊艙與Stewart平臺共同組成隔振系統，吊艙的質心位置對系統的性能有較大影響。系統完全解耦時，即使在共振時線振動也不會引起系統的角振動響應。例如在Simulink 模型中在系統x向施加與x向共振頻率相同的定頻激勵(頻率為5.96 Hz，幅值為10 mm)，隔振系統的分析結果如圖5所示。

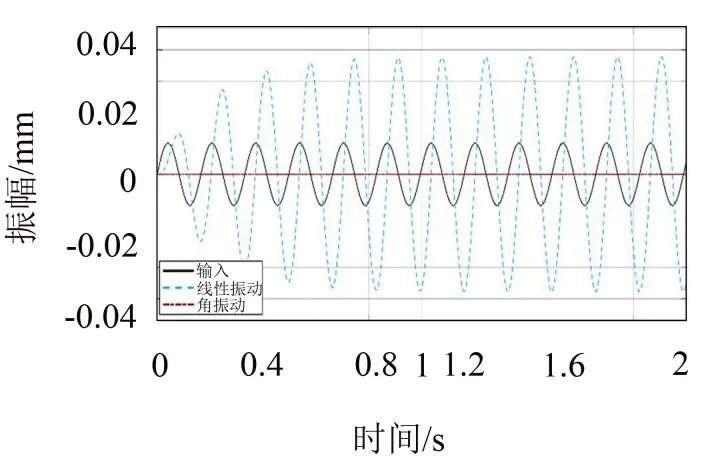
圖5 隔振系統正弦響應結果(5.96 Hz,10 mm)

從分析結果可以看出：系統在5.96 Hz處振幅被放大；線振動響應幅值為37.7 mm，放大倍數為3.77倍，同時角振動的幅值不超過1.5×10-5rad。可以認為線振動激勵沒有引起角振動響應。當進一步調整吊艙的質心位置hc時，計算相應的角振動響應如圖6所示。

從圖6 可以看出：吊艙的質心位置對隔振系統的解耦影響較大，質心位置改變可以引起較大的角振動響應。如果要使角振動響應小于0.01 Rad(34.4′)，則質心的位置公差不應超過±2 mm。

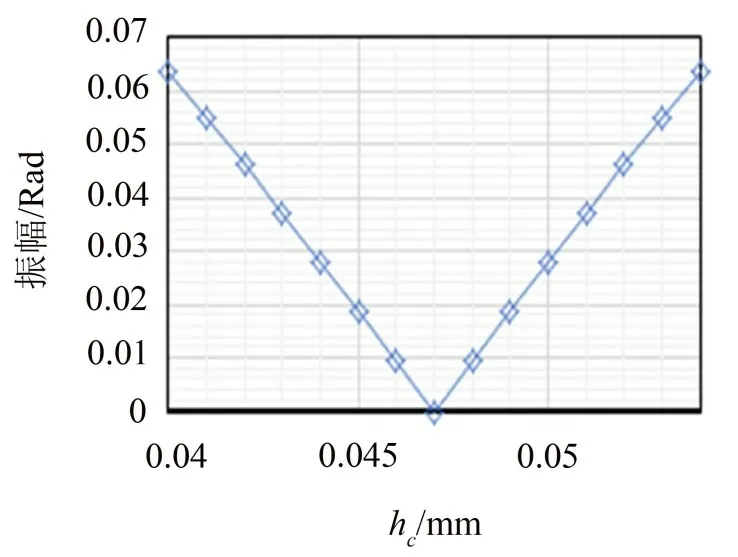
圖6 hc對角振動振幅的影響

3.2 白噪聲中隔振系統的振動響應

給Simulink 模型施加白噪聲隨機激勵時，計算的結果如圖7所示：其中圖7(a)為隔振系統徑向的振動響應，圖7(b)為隔振系統軸向的振動響應。圖中的灰色線條為白噪聲激勵，藍色線條為線振動響應，紅色線條為角振動響應。

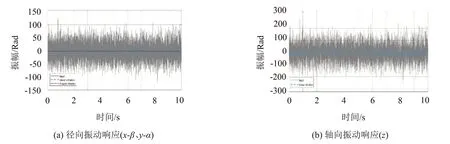
圖7 白噪聲激勵下隔振系統的振動響應

從圖中可以看出：系統的角振動響應基本為0，說明系統已經完全解耦，線振動激勵不會引起相應的角振動響應。隔振系統性能良好，隔振后系統的振幅已經被很大程度地減弱了，衰減幅度超過78%。

4 結語

通過理論計算研究了Stewart 平臺隔振系統的設計方法，采用有限元仿真分析以及虛擬試驗對設計方法進行分析對比與驗證。

(1)經過等剛度解耦設計之后的隔振系統可以有效地實現3 個方向上模態頻率相同且完全解耦。三軸向的模態頻率差別不大于7.8%，線振動引起的角振動的幅值不超過1.5×10-5rad。理論模型與仿真分析吻合度很高，驗證了模型的工程應用價值。

(2)光電吊艙的質心位置對隔振系統的解耦影響較大，質心位置公差不超過±2 mm 時，耦合產生的角振動響應可以基本滿足要求。

(3)所設計的隔振系統性能良好，可以有效地使振動衰減，振動衰減幅度超過78%，研究對光電吊艙隔振系統的設計具有一定的指導意義。由于目前試驗條件的限制，隔振系統的性能沒有在真實試驗中被測試，需要在今后工程實踐中進一步驗證。