航行體開槽包裹式緩沖頭帽結構設計及其降載性能*

施 瑤，劉振鵬，潘 光，高興甫

（1. 西北工業大學航海學院，陜西 西安 710072；2. 西北工業大學航海學院無人水下運載技術工業和信息化部重點實驗室，陜西 西安 710072）

隨著軍事科技的發展，各種新型的軍事武器裝備不斷出現，其中采用固定翼飛機、直升飛機投放或火箭助飛等新型發射方式的跨水空介質航行體具有防區外發射、突防能力強及隱蔽性高等優點，成為了軍事武器裝備發展的熱點。攻擊過程中，需要由空中彈道轉變為水中彈道，該類航行體將經歷一個跨介質高速入水的過程。在該過程中，由于介質密度的突變以及復雜的湍流流動等原因，航行體將承受巨大的沖擊載荷，引起殼體結構的動態響應，導致殼體結構發生彈塑性變形，甚至造成斷裂、破損和屈曲；或對航行體的彈道軌跡產生影響，致使航行體入水過程中發生忽撲、跳水和彈道失控等嚴重問題。因此，減小航行體高速入水時受到的沖擊載荷，確保安全入水，是至關重要的。

比較常見的降載方法有：在航行體尾部掛載降落傘，降低入水速度并穩定空投彈道[1-2]；利用航行體的頭部噴出氣體，緩和入水沖擊環境[3-5]；在航行體頭部安裝一個氣囊[6]或者緩沖頭帽，利用材料的變形和破碎來吸收航行體高速入水過程中承受的巨大沖擊能量。嚴忠漢[7]討論了入水彈頭緩沖材料的動態特性，提出了切片法、臨界設計狀態等概念，這些概念對后續緩沖頭帽的設計具有重要意義。王永虎等[8]引進了聚氨酯泡沫塑料在沖擊加載條件下的本構關系式，代替了傳統的三段式經驗模式，分析了航行體垂直入水情況下緩沖器的動態緩沖特性。早期，對于緩沖頭帽的研究大多基于實驗研究，或者對單一的緩沖材料特性進行分析。實驗研究存在耗資昂貴、可重復差等問題，對單一緩沖材料的特性分析反映到實際的入水過程中存在較大的局限性，因此如今對于緩沖頭帽的研究大多基于數值計算手段。其中比較常用的算法為任意的拉格朗日-歐拉（arbitrary Lagrangian-Eulerian, ALE）算法[9]，該算法為解決作用過程復雜的水氣固多介質耦合問題提供了新的求解思路。Wang 等[10]研究了輕型金字塔夾層板結構低速入水時的流固耦合動態響應，獲得了沖擊壓力和結構變形的特性。李建陽等[11]通過對大型返回艙入水時不同工況的數值計算，分析了入水速度和入水角度對沖擊載荷特性的影響。胡明勇等[12]建立了低亞聲速射彈垂直入水的流固耦合數值計算模型，對入水空泡、流場與彈道間的多介質耦合問題進行了數值求解。顏彬等[13]在考慮彈體內部支撐結構的情況下，對彈體入水時結構的力學響應進行了數值計算。Wu 等[14]對裝備緩沖頭帽的射彈的入水過程進行了數值計算，提出了計算射彈入水過程中減速度的經驗公式。Li 等[15]對裝備緩沖頭帽的航行體的入水過程進行了數值計算，重點研究了入水過程中罩殼的變形失效形式。魏海鵬等[16]對適用于直徑為324 mm 的航行體的緩沖組件進行了數值研究，發現在撞水時罩殼的頭部和預置溝槽處會出現明顯的應力集中現象，分層的緩沖泡沫出現了二次緩沖等現象。

對于航行體入水緩沖頭帽的研究不乏公開報道，但是現有的研究主要是針對于直徑為324 mm 的小尺度航行體入水情形，適用于大尺度航行體高速安全入水的緩沖頭帽結構設計及其降載性能分析研究較少。直徑為533 mm 的大尺度航行體在高速入水時，所面臨的沖擊環境更為極端，流體對航行體殼體結構的作用更為劇烈，小尺度航行體降載結構的相關設計理論難以直接應用于大尺度航行體。

本文中，利用LS-DYNA 軟件，并基于ALE 算法，建立裝備緩沖頭帽的航行體高速入水數值模型，對適用于大尺度航行體高速入水的開槽包裹式緩沖頭帽的緩沖性能進行數值研究，探究其緩沖性能的相關影響因素，以期為新型緩沖頭帽的結構設計提供指導。

1 緩沖頭帽

根據魚雷緩沖頭帽設計可行域[17]，本文中所設計的緩沖頭帽主要由外部開槽罩殼和內部緩沖材料組成。罩殼可以承受航行體投放時的氣動壓力，保證緩沖頭帽在入水之前整體結構的完整性，同時使裝備緩沖頭帽的航行體在空中飛行時阻力較小，提高航行體的飛行速度，增大航行體的投送距離；緩沖材料在入水過程中依靠自身變形吸收巨大的沖擊能量，從而降低作用在航行體上的沖擊載荷。

1.1 罩 殼

航行體的外形參考魚雷MK48，最大直徑為533 mm，總體長度為5 850 mm，如圖1 所示。為了保證裝備緩沖頭帽后的航行體具有良好的氣動外形，本文中所設計的罩殼采用尖拱體外形，罩殼圓柱段外徑為555 mm，厚度為5 mm，尖拱段長度為600 mm，圓柱段長度為700 mm，如圖2所示。為了減小緩沖頭帽對航行體入水彈道的影響，使它更容易與航行體分離，沿罩殼的周向開8 個強度減弱槽，軸向開槽長度為900 mm，開槽深度為3 mm，軸向開槽角度為15°，如圖3 所示。

圖1 航行體外形Fig. 1 Shape of the vehicle

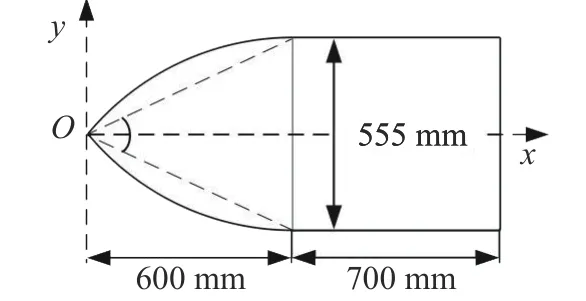
圖2 罩殼外形Fig. 2 Shape of the nose cap

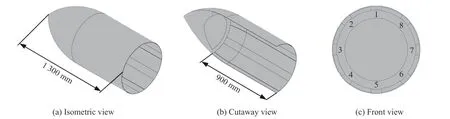
圖3 罩殼開槽示意圖Fig. 3 Schematic diagrams of the slotted nose cap

1.2 緩沖件

本文中設計了一種開槽包裹式緩沖件，如圖4 所示，緩沖件內部線型與航行體頭部線型一致，能夠完全包裹航行體頭部曲線段，二者接觸面積大，在航行體入水角度較小時，可以有效地保護航行體頭部殼體設備。同時，為了避免緩沖件被壓實后不容易破碎的問題，沿緩沖件周向均勻開8 個槽，開槽底部距離緩沖件前端100 mm，緩沖件開槽前端深度為50 mm，緩沖件包裹段后端厚度為6 mm，開槽深度為3 mm。罩殼主要發生撐進破壞[17]，適當增大罩殼前段厚度有利于它破碎，因此緩沖件前端向后縮進一部分，罩殼前段加厚。航行體裝備緩沖頭帽后的整體示意圖如圖5 所示。

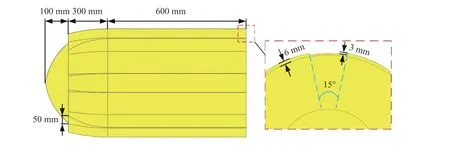
圖4 開槽包裹式緩沖件Fig. 4 A slotted wrapping buffer

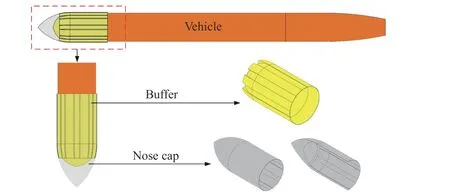
圖5 航行體裝配緩沖頭帽后整體Fig. 5 The whole body of the vehicle assembled with the buffer head cap

2 計算模型

有限元算法中比較常見的算法有拉格朗日算法與歐拉算法以及任意的拉格朗日-歐拉算法（ALE 算法）。拉格朗日算法的網格會隨著物質進行運動，對結構邊界的捕捉比較精確，但是當結構發生大變形時，可能導致網格出現畸變的現象，引起計算結果不準確。歐拉算法的網格是固定不動的，物質在網格之間進行輸運，對網格的變形沒有限制，但對于結構邊界的捕捉精度不夠。對于航行體高速入水的問題，選擇ALE 算法進行求解，發揮二者的優勢，利用拉格朗日網格求解航行體及緩沖頭帽的變形破碎，捕捉精度高，利用歐拉網格來求解自由液面的大變形，數值計算穩定。

2.1 ALE 算法基本原理

ALE 算法的控制方程由質量守恒方程、動量守恒方程和能量守恒方程組成[18]。

(1)質量守恒方程：

式中：ρ 為流體的密度；x為歐拉坐標；v為流體的速度；u為網格的速度；w=v-u；E為流體的內能；σij為應力張量的分量；b為流體所受的體積力載荷。

ALE 算法的基本實現過程如下[19]：

(1)先進行拉格朗日步計算，單元網格隨著材料運動而變形，保持變形后的物體邊界條件，對內部重新劃分網格，網格的拓撲關系保持不變，稱為光滑步。

(2)將變形網格中的單元變量和節點速度矢量輸運到新網格中，稱為對流步。一般每個單元解的各種變量都要進行輸運，要輸運的數量取決于材料模型。

ALE 算法中流固耦合力計算方法如圖6 所示。對于結構節點，在每一時間步通過相對速度(vs-vf)更新侵徹深度d，結構節點定義為從節點，流體節點定義為主節點，使用流體單元的等參坐標計算主節點的位置。當t=0 時，假定d(0)=0，流體節點和結構節點重合；當t(n)=t(n-1)+Δt，侵徹向量通過下式更新：

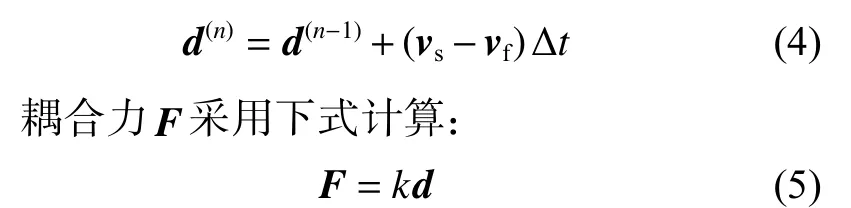
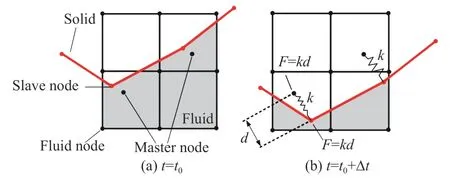
圖6 流固耦合算法Fig. 6 Algorithm of fluid-structure interaction

式中：k為基于主從節點質量模型特性的剛度系數。

2.2 有限元模型

選定一個局部坐標系(Oxyz)和一個全局坐標系(O0x0y0z0)[20]，如圖7 所示。其中，全局坐標系原點O0處于航行體入水點；O0x0軸位于水平面內，此軸的方向指向航行體的前進方向，稱為參考航向；O0y0軸垂直于地面指向上方，稱為鉛垂軸；O0z0軸處于水平面內，垂直于x0O0y0平面，方向由右手坐標法則確定。局部坐標系原點O位于航行體重心處，Ox軸處于航行體對稱面內，與航行體幾何對稱軸一致，指向航行體頭部，稱為航行體縱軸；Oy軸位于航行體縱對稱面內，垂直于Ox軸，指向上方，稱為航行體立軸；Oz軸垂直于xOy平面，從航行體尾部觀察，Oz軸指向右方，稱為航行體橫軸。定義Ox軸與水平面的夾角為入水角θ。

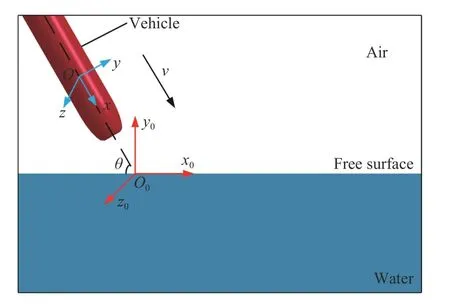
圖7 坐標系的定義Fig. 7 Definition of coordinate systems

考慮到航行體殼體以及罩殼在入水過程中的彈塑性變形，對它們采用*MAT_PLASTIC_KINEMATIC材料模型。航行體殼體材料選用鋁合金，該鋁合金的密度為2 700 kg/m3，彈性模量為75 GPa，泊松比為0.33，屈服應力為275 MPa，剪切模量為1.33 GPa。罩殼材料選用不飽和聚酯樹脂復合材料，該材料的密度為1 160 kg/m3，彈性模量為3.5 GPa，泊松比為0.34，屈服應力為101 MPa。對緩沖件采用*MAT_PLASITIC_KINEMATIC 材料模型，并設置失效應變，用于模擬緩沖件的破碎過程。當某個單元的應變超過失效應變時，該單元即失效，不再參與計算。不同密度的發泡材料的緩沖性能不同[21]，所采用緩沖件的材料為硬質聚氨酯泡沫，該泡沫的密度為90 kg/m3，彈性模量為129 MPa，泊松比為0.024，失效應變為0.5，阻尼系數為0.5。

對水和空氣等流體采用*MAT_NULL 材料模型，需要采用*EOS_GRüNEISEN 狀態方程[22]描述水的運動：

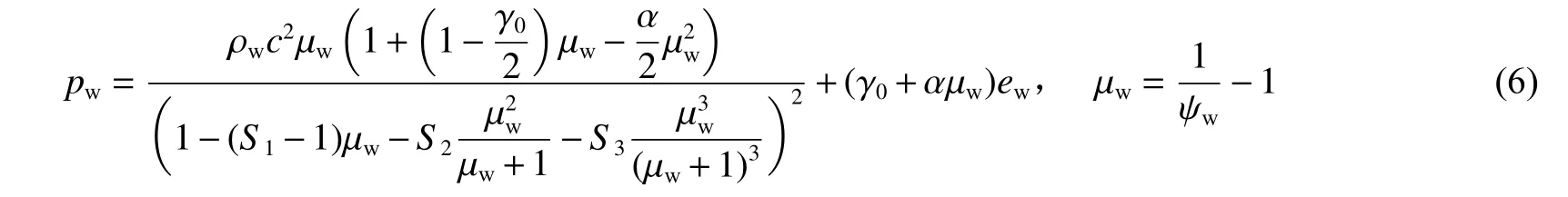
式中：pw為水的壓力，c為水中聲速，γ0為Grüneisen 常數，α 為γ0的一階體積修正量，ew為水的體積內能；S1、S2、S3為斜率系數，ψw為水的相對體積。本文中：c=1 480 m/s,S1=2.56,S2=-1.986,S3=0.226,S3=0.226；水的初始體積內能ew0=0，水的初始相對體積ψw0=1。

采用*EOS_LINEAR_POLYNOMIAL 狀態方程[23]描述空氣的運動：

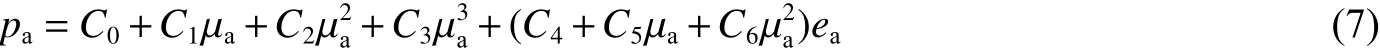
式中：C1、C2、C3、C4、C5、C6為多項式系數；ea為空氣的體積內能； μa=1/ψa-1 ，ψa為空氣的相對體積。本文中：C0=C1=C2=C3=0,C4=C5=0.4,C6=0；空氣的初始體積內能ea0=250 kJ/m3。

2.3 網格無關性驗證

流體網格尺寸與結構網格尺寸之比：

式中：LE為流體單元網格的特征尺寸；LL為結構單元網格的特征尺寸。航行體的入水沖擊加速度用無量綱的系數cd表示：

式中：m為航行體的質量，a為航行體的入水加速度，R為航行體的最大半徑，v為航行體的入水速度。

航行體網格尺寸為10 mm，N取值為1～5；水和空氣單元的網格尺寸一致，分別為10、20、30、40 和50 mm。航行體的入水速度為100 m/s，入水角度為90°。不同網格比例下的沖擊加速度系數時程曲線、加速度峰值系數cd,p如圖8 所示，可以看出，隨著流-固網格比例的減小，加速度峰值和脈寬逐漸增大，當N=4 時計算結果就滿足了收斂性要求。綜合考慮了計算精度的要求及所需要的計算時間，航行體的網格尺寸設置為10 mm，水和空氣的網格尺寸均設置為40 mm，同時，為減小壁面效應對計算結果的影響，空氣域和水域的尺寸均設置為10 m×6.4 m×6 m，水域底部設置為固定邊界，其余邊界條件設置為無反射邊界條件，總體劃分網格數為8 763 225，如圖9 所示。

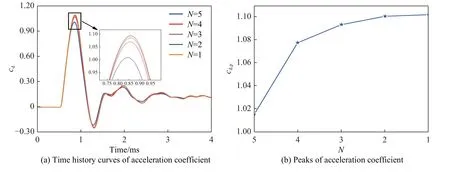
圖8 不同網格尺寸下的加速度系數及其峰值Fig. 8 Time history curves of acceleration coefficient and its peaks under different mesh sizes

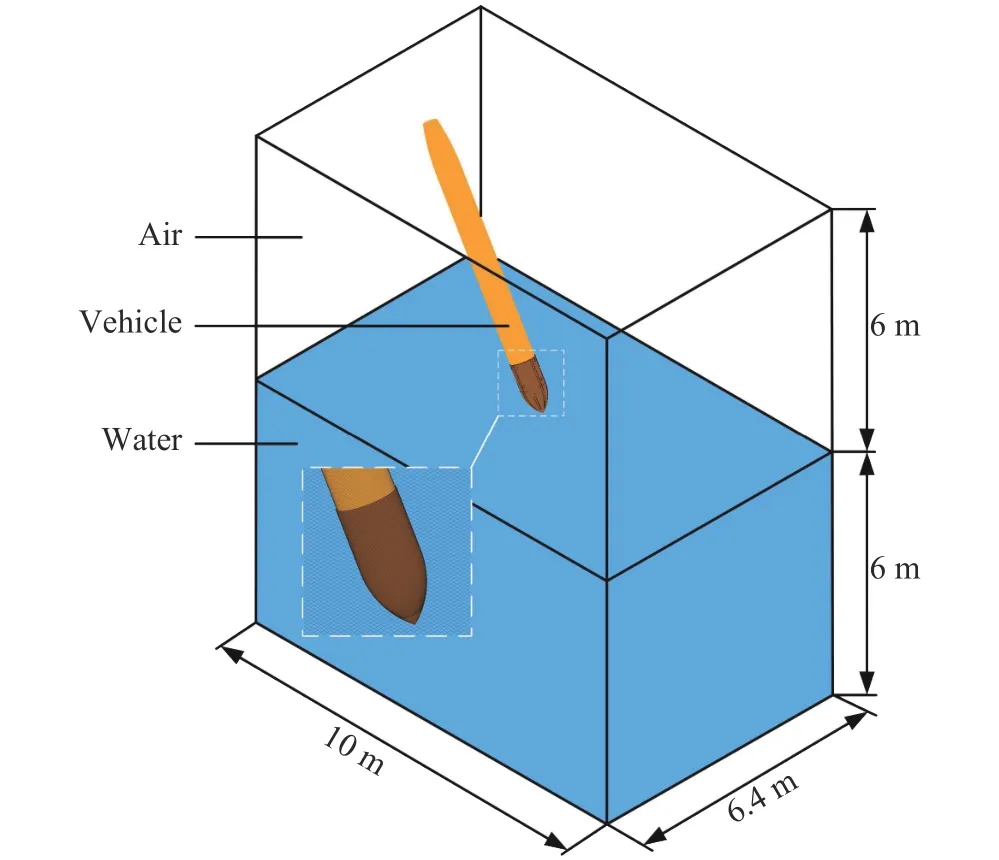
圖9 計算域Fig. 9 Computational domain

2.4 數值計算結果驗證

為了驗證數值計算模型的正確性與準確性，開展了航行體縮比模型頭段帶緩沖頭帽高速入水實驗。實驗現場布局如圖10 所示，采用高壓空氣作為模型的動力來源；在模型內部安裝測試裝置，記錄模型的加速度信息；利用高速攝像機捕捉模型的位置姿態及入水空泡演變信息；模型的入水速度為101 m/s，入水角度為60°。

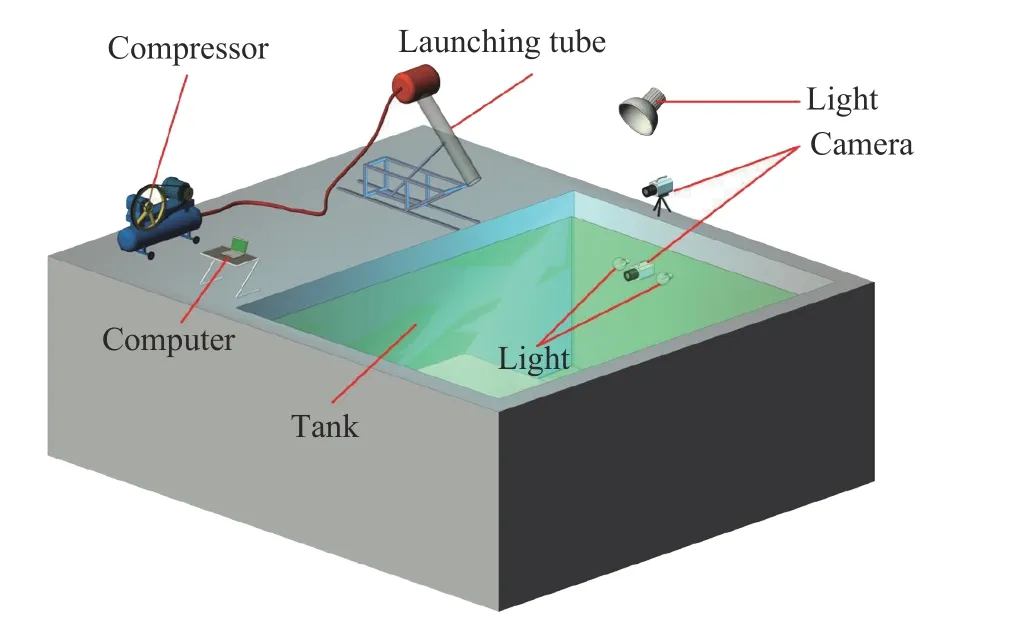
圖10 實驗現場布局Fig. 10 Experimental layout

利用圖像處理技術，將數值計算的空泡演變宏觀輪廓進行提取，并與實驗中高速攝像機拍攝所得的航行體入水空泡輪廓進行疊加對比，如圖11 所示。從兩者的空泡輪廓和演變規律來看，本文中所建立的裝備緩沖頭帽的航行體高速入水數值計算模型，能較真實地反映實際情況中航行體高速入水的空泡演變宏觀特性。

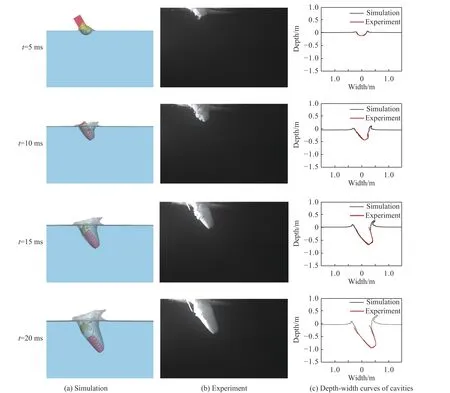
圖11 數值計算與實驗空泡的對比Fig. 11 Comparison of cavities between simulation and experiment

圖12 為航行體的入水沖擊加速度數值計算結果和實驗測試結果的對比?？梢钥闯觯瑪抵涤嬎愫蛯嶒灉y得的加速度的變化趨勢基本一致，兩者軸向加速度峰值相對誤差為6.72%，徑向加速度峰值相對誤差為7.52%，兩者沖擊加速度峰值和峰值脈寬均吻合良好，滿足實際工程中數值計算的精度需求，能夠支撐后文的數值計算。

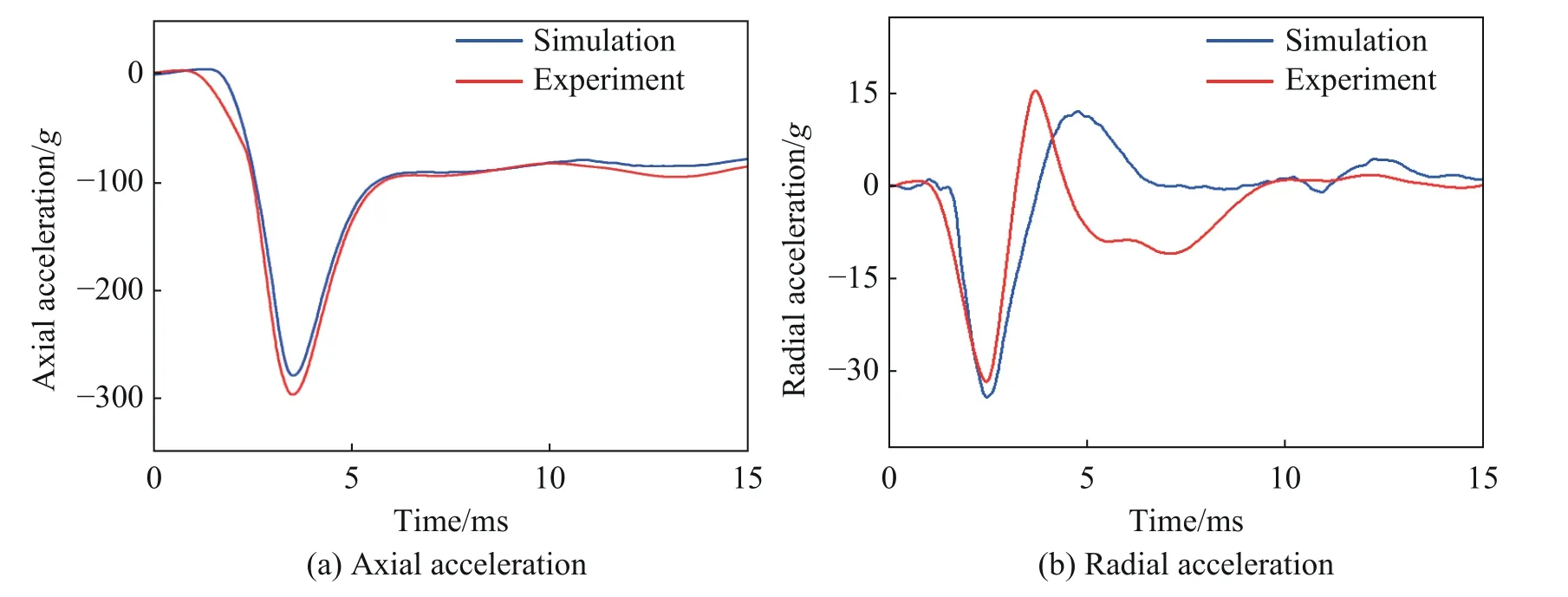
圖12 數值計算與實驗測試加速度的對比Fig. 12 Comparison of accelerations between simulation and experiment

3 結果與分析

3.1 入水流場演化特性和頭帽破碎過程

圖13～14 為航行體以100 m/s 的速度垂直入水和以60°斜入水時的空泡演化圖像和緩沖材料破壞圖像，為了觀察緩沖材料的變形破碎，將罩殼隱藏。初始時刻時，整體結構位于水面上方一定的距離，5 ms 時緩沖頭帽已經接觸到水面，水體被排開，空泡輪廓擴張，緩沖頭帽破裂后刺破了空泡壁面，使空泡輪廓變得粗糙。航行體垂直入水時，空泡輪廓基本對稱，水面上方液面隆起，有液體飛濺。當航行體以60°斜入水時，由于迎水面與背水面的速度不一致（見圖15），導致了兩側的水壓不同，壓力低的一面空泡擴張速度快，壓力高的一面空泡擴張速度慢。因此，航行體斜入水時產生的空泡是非對稱的，同時，航行體除了受到一個較大的軸向載荷外，其徑向也將承受一個不可忽視的沖擊載荷。裝備緩沖頭帽的航行體斜入水時，緩沖頭帽的破碎不對稱，相較于垂直入水時，緩沖頭帽破碎的范圍更大，從圖13～14 可以看出，不管是垂直入水還是斜入水，緩沖頭帽都能發生較大程度的破損，并在入水后期與航行體完全脫離，從而不影響航行體后續的入水彈道。

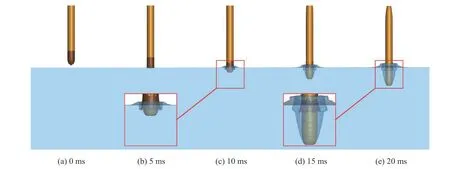
圖13 航行體以100 m/s、90°入水時流場演化和緩沖件的破壞過程（隱藏罩殼）Fig. 13 Flow field evolution and failure process of buffer when the vehicle enters water at 100 m/s and 90° (hide the nose cap)

圖14 航行體以100 m/s、60°入水時流場演化和緩沖件的破壞過程（隱藏罩殼）Fig. 14 Flow field evolution and failure process of buffer when the vehicle enters water at 100 m/s and 60° (hide the nose cap)

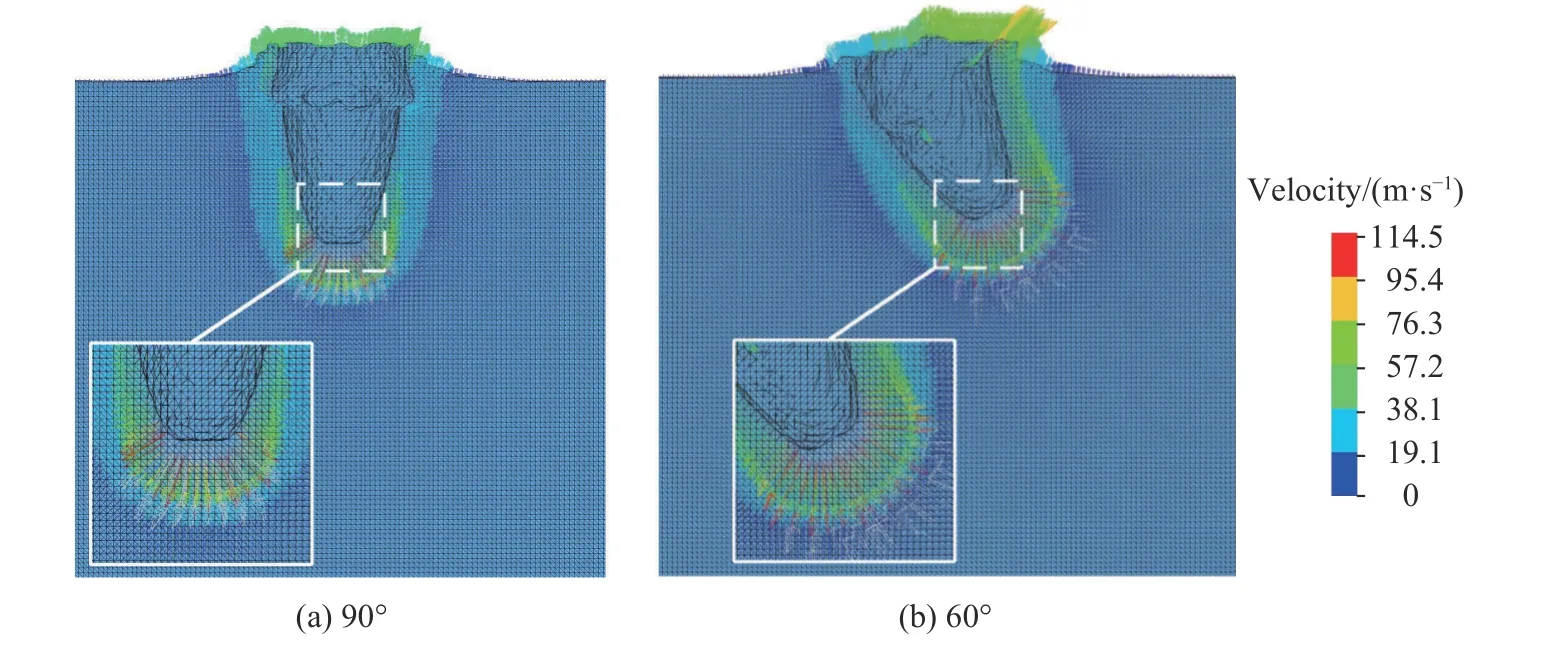
圖15 航行體以100 m/s 的速度在不同入水角度下20 ms 時水體的速度矢量Fig. 15 Vectors of velocity of the water when the vehicle enters water at 100 m/s and different angles at 20 ms

3.2 緩沖材料的破壞特性

圖16～17 分別為航行體以100 m/s 的速度垂直入水和60°入水角斜入水過程中緩沖材料在不同時刻的等效應力云圖。

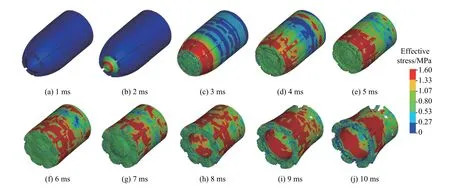
圖16 航行體以100 m/s、90°入水角入水時緩沖材料的等效應力分布Fig. 16 Distribution of effective stress of the buffer when the vehicle enters water at 100 m/s and 90°

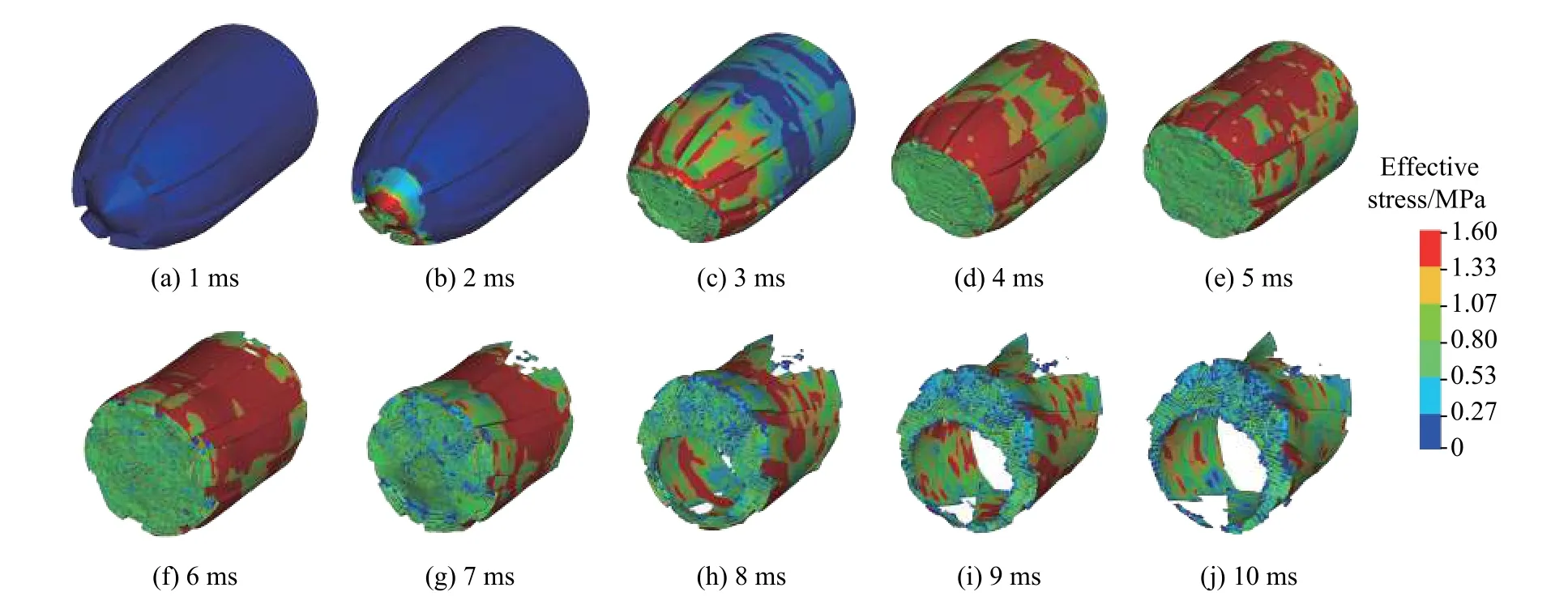
圖17 航行體以100 m/s、60°入水角入水時緩沖材料的等效應力分布Fig. 17 Distribution of effective stress of the buffer when the vehicle enters water at 100 m/s and 60°

可以明顯看出，在緩沖頭帽撞水時，緩沖材料內部出現了明顯的應力集中現象；應力首先出現在緩沖材料的前端，并以應力波的形式向緩沖材料的后端傳播；在航行體垂直入水初期，應力在緩沖材料內部呈現較均勻的分層現象。而在航行體以60°斜入水時，由于緩沖材料兩邊觸碰到水的時刻不同，下部先受到水的擠壓作用，先出現應力集中現象，因而導致入水初期應力在緩沖材料內部分布不均勻。從圖中也可以看出，7 ms 左右緩沖材料被航行體擊穿，此時航行體頭部直接接觸到水，航行體受到的沖擊載荷到達峰值。

3.3 入水速度和入水角度對降載性能的影響

探究了不同入水速度和不同入水角度下緩沖頭帽的降載性能。當入水角度為90°時，入水速度分別為100、150、200、250 和300 m/s；當入水速度為100 m/s 時，入水角度分別為60°、70°和80°。

圖18(a)為裝備緩沖頭帽的航行體在不同入水速度下垂直入水時的加速度時程曲線，圖18(b)為未裝備緩沖頭帽的航行體在不同入水速度下垂直入水時的加速度時程曲線。從圖18 可以看出，隨著航行體入水速度的不斷升高，沖擊加速度的峰值不斷增大，脈寬不斷增大，緩沖材料被擊穿的時刻不斷提前，緩沖頭帽的緩沖性能減弱，入水速度為300 m/s 時，航行體加速度峰值減小22.17%。

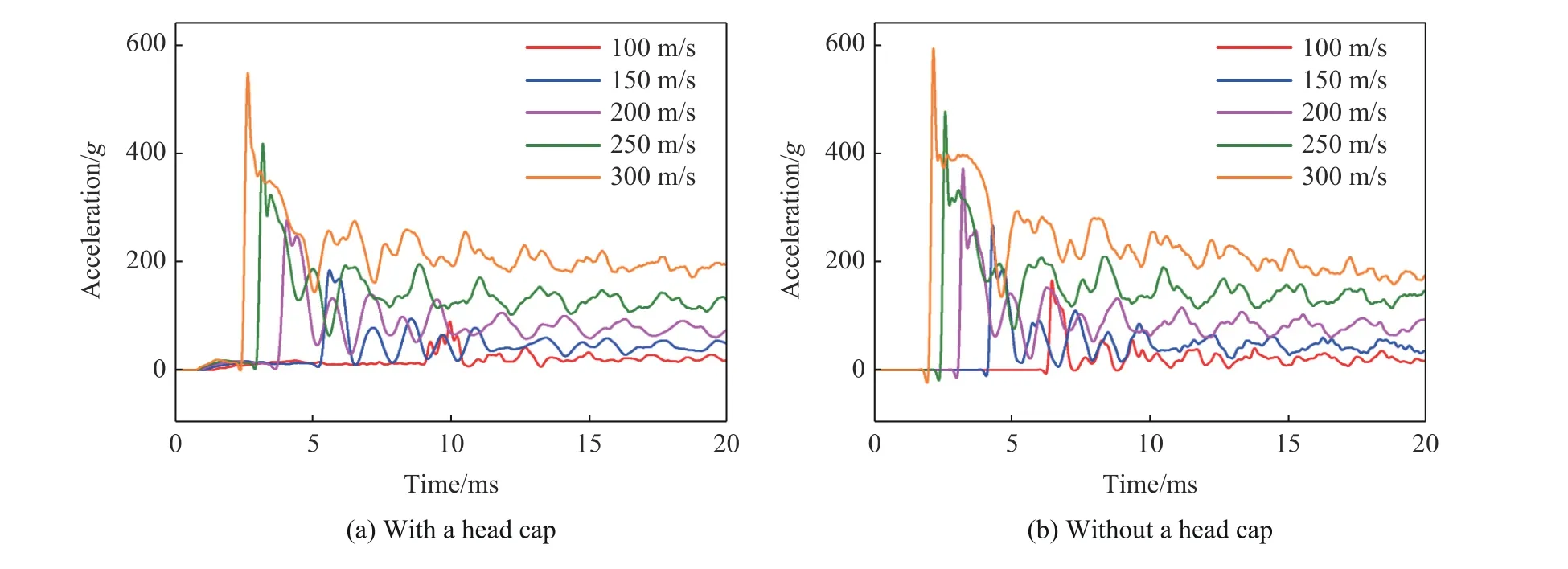
圖18 不同的航行體以不同入水速度垂直入水時的加速度時程曲線Fig. 18 Time-history curves of acceleration when different vehicles enter water vertically at different velocities

圖19～20 為航行體以100 m/s 的速度在不同入水角度下的加速度時程曲線?？梢钥闯?，在入水速度相同時，隨著入水角的增大，軸向加速度峰值逐漸增大，徑向加速度峰值逐漸減小，緩沖頭帽對航行體軸向和徑向加速度峰值的減小率越大，當入水角度為60°時，對軸向加速度峰值的減小率為31.83%，對徑向加速度峰值的減小率為66.80%。

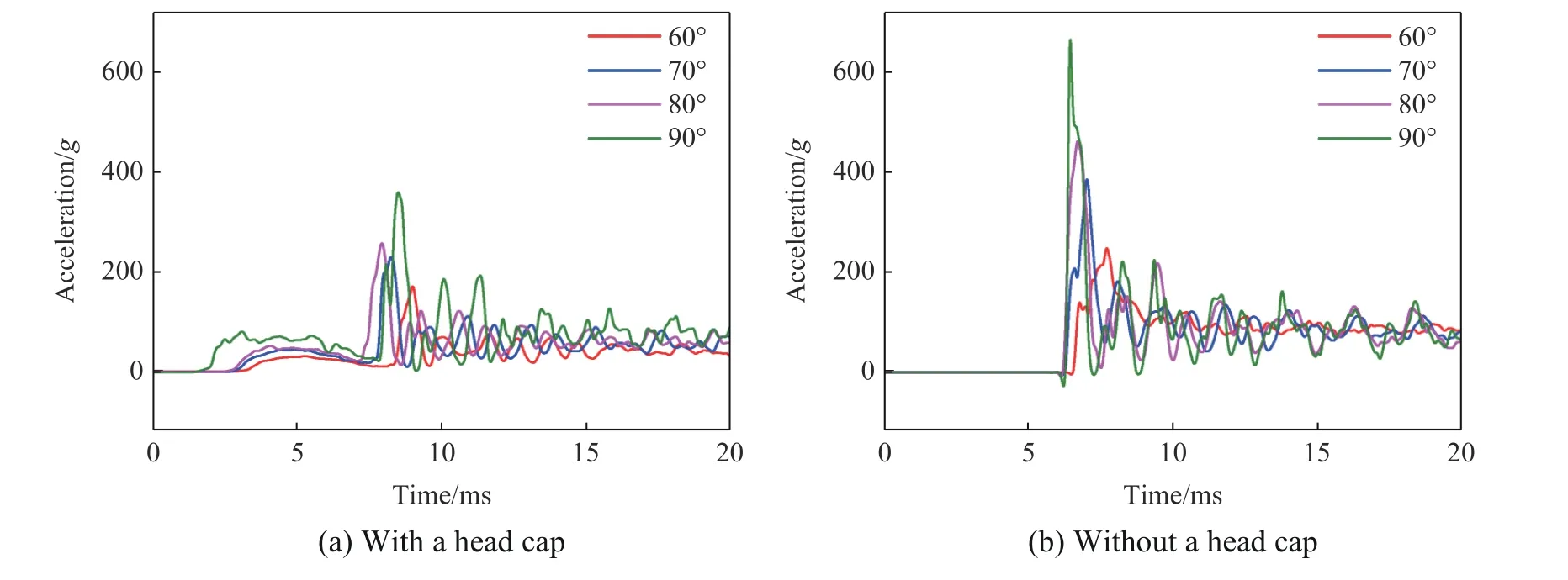
圖19 不同的航行體以100 m/s 的速度在不同入水角度下的軸向加速度時程曲線Fig. 19 Time-history curves of axial acceleration when different vehicles enter water at 100 m/s and different angles

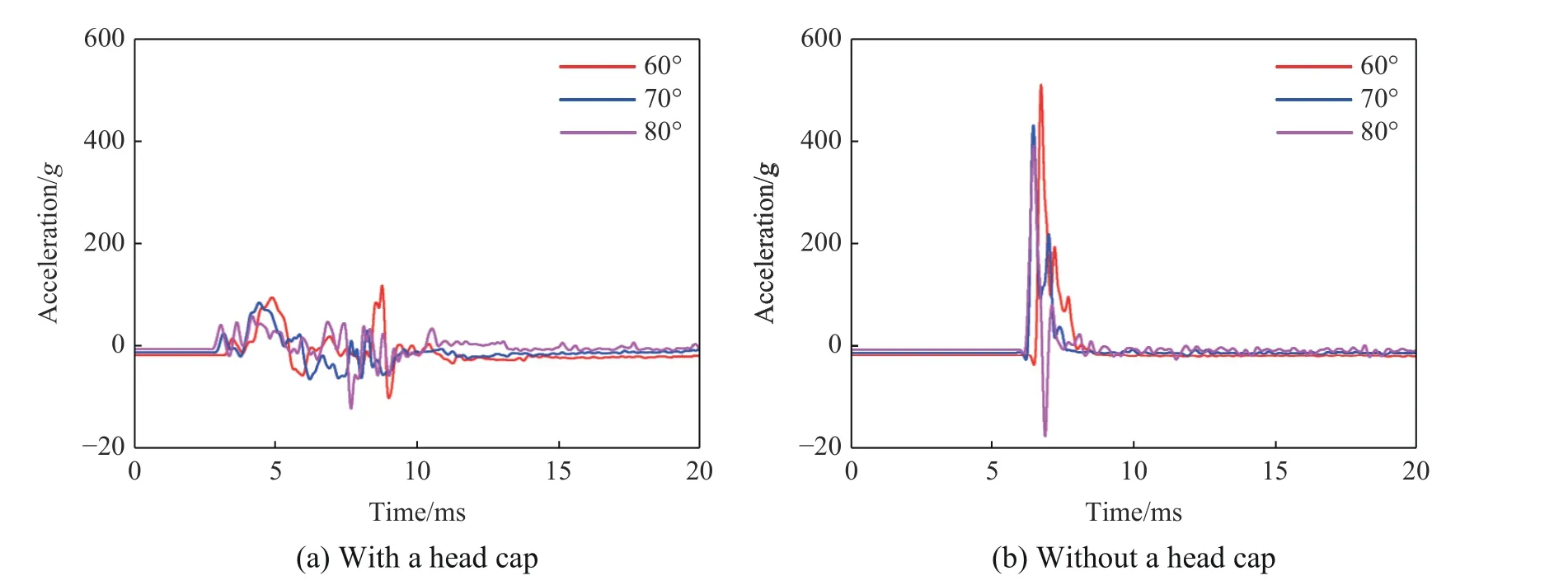
圖20 不同的航行體以100 m/s 的速度在不同入水角度下的徑向加速度時程曲線Fig. 20 Time-history curves of radial acceleration when different vehicles enter water at 100 m/s and different angles

4 結 論

設計了適用于大尺度航行體高速安全入水的尖拱體外形開槽包裹式緩沖頭帽，并給出了詳細的設計參數?；贏LE 算法，對裝備開槽包裹式緩沖頭帽的航行體高速入水過程進行了數值模擬，并用航行體頭段縮比模型高速入水實驗驗證了所建立數值模型的正確性與準確性。從不同角度，對所設計的開槽包裹式緩沖頭帽緩沖性能進行了分析，主要得到以下結論。

(1)裝備緩沖頭帽的航行體在高速垂直入水時，受緩沖頭帽破碎形態的影響，產生了壁面較粗糙的對稱空泡；而斜入水時，受兩側水流速度不一致的影響，產生了非對稱空泡，對航行體的受力分布產生了不可忽視的影響。

(2)航行體垂直入水時，應力集中區域首先在緩沖材料頭部出現，并以應力波的形式向后快速傳遞；垂直入水時應力分布呈現較均勻的分層現象，斜入水時應力分布也呈現分層現象，但不均勻；應力區域的分布可為緩沖材料的結構設計提供指導。

(3)隨著航行體入水速度的提高，沖擊加速度的峰值也隨之增大，緩沖頭帽被擊穿的時刻提前，降載性能逐漸下降，以300 m/s 的速度垂直入水時，沖擊加速度峰值減小22.17%；當航行體斜入水時，入水角度越大，緩沖頭帽的降載效果越好，入水速度為100 m/s、入水角度為60°時，軸向沖擊加速度峰值減小31.83%，徑向沖擊加速度峰值減小66.80%，緩沖頭帽的降載隔沖作用給航行體高速安全入水提供了保證。