非藥物干預措施對COVID-19模型的影響
白雪花,薛亞奎
(中北大學 理學院, 太原 030051)
0 引言
COVID-19是一種傳染性極強的疾病,在全世界范圍內引起了持續和重大的公共衛生問題,2020年1月2日至2021年6月19日,COVID-19的迅速傳播已導致全球約有1.8億確診病例和近400萬死亡病例[1]。COVID-19主要通過呼吸道飛沫或密切接觸傳播,并且人接觸了帶有病毒的物品也可能被感染,一旦感染COVID-19,患者最初沒有明顯的臨床癥狀,稱為無癥狀感染,在特定時間后,無癥狀感染會發展為有癥狀感染[2-4]。為了預防和減少COVID-19的傳播,除了接種疫苗外最關鍵的做法是采取一些非藥物干預措施,如保持社交距離、自我隔離或隔離感染者、戴口罩、追蹤密切接觸者和大面積核酸檢測等[5]。保持社交距離的目的是減少社區中人與人之間的互動,由于無癥狀感染者通過飛沫傳播需要一定距離,因此保持嚴格的社交距離可以減少疾病的傳播。追蹤密切接觸者和核酸檢測是對密切接觸者進行限制或隔離,目的是監測他們的癥狀并確保及早發現病例,防止疾病的進一步傳播[6-7]。
數學模型對傳染病的控制有重要意義,最近,許多專家利用不同的數學模型來研究COVID-19的傳播模式[8-10]。Annas等[11]提出SEIR模型,該模型使用印度尼西亞COVID-19病例的二次數據來預測未來病毒的流行趨勢。Rafiqa等[12]提出雙峰態SITR模型,該模型通過將易感人群劃分為2個不重疊的亞群體來模擬COVID-19的傳播。Fanelli等[13]提出了基于非線性微分方程的數學模型,研究了中國、意大利和法國等疫情嚴重國家的COVID-19感染動態。Atangana[14]提出了新的分形-分數階微分算子和積分算子的數學模型,探討了封鎖社會對COVID-19的影響。
無癥狀感染是COVID-19最大的特點,也是控制疾病傳播的關鍵,而預防COVID-19的傳播, 除接種疫苗外唯一的方法是實施非藥物干預措施。因此建立了包含無癥狀和有癥狀感染的SEIAR模型,研究了保持社交距離、追蹤密切接觸者和核酸檢測對COVID-19動態的影響。
1 模型的建立
將總人群N(t)分為5類:易感者S(t)、潛伏者E(t)、有癥狀感染者I(t)、無癥狀感染者A(t)、恢復者R(t),則N(t)=S(t)+E(t)+I(t)+A(t)+R(t)。在被感染的人群中,有癥狀感染者可以將病毒傳染給其他人;無癥狀感染者不表現出任何癥狀,但會將病毒傳染給其他人。基于以上討論,建立以下模型:
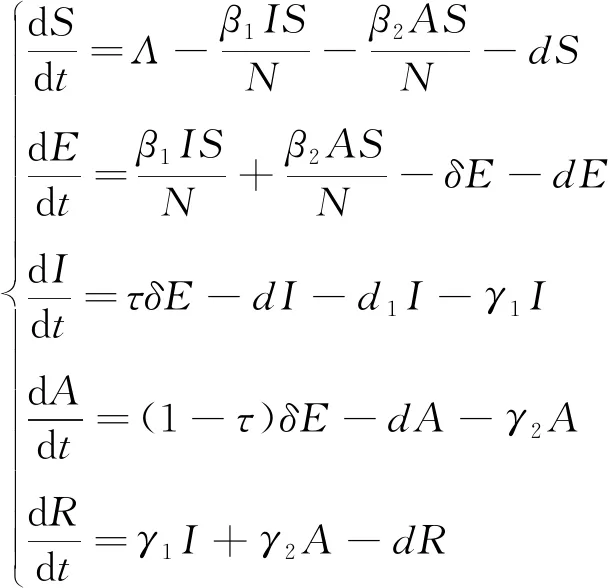
(1)
式中:Λ為出生率;d為自然死亡率;β1為有癥狀感染者的有效接觸率;β2為無癥狀感染者的有效接觸率;δ為潛伏者到染病者(包括有癥狀感染者和無癥狀感染者)的轉移率;潛伏者分別以τ和1-τ的比例轉移為有癥狀感染者和無癥狀感染者;d1為因病死亡率;γ1為有癥狀感染者的恢復率;γ2為無癥狀感染者的恢復率。

2 基本再生數和平衡點的存在性
根據下一代矩陣法[15]計算基本再生數R0,可得
式中:
R1表示有癥狀感染者產生COVID-19新感染的平均數,R2表示無癥狀感染者產生COVID-19新感染的平均數。
定理1當R0>1時,系統(1)在Ω內存在唯一的地方病平衡點P*(S*,E*,I*,A*,R*)。
證明令系統(1)的方程右端等于0,求解得
式中:
(2)
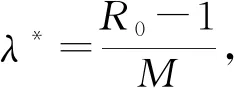
當R0>1時,有λ*>0,即系統(1)在Ω內存在唯一的地方病平衡點P*(S*,E*,I*,A*,R*)。
3 平衡點的穩定性
定理2當R0<1時,系統(1)的無病平衡點P0在Ω內是局部漸近穩定的。
證明系統(1)在無病平衡點P0處的Jacobian矩陣為:
矩陣J(P0)的特征方程為:
(λ+d)2(λ3+a1λ2+a2λ+a3)=0
式中:
a1=3d+δ+d1+γ1+γ2>0
a2=(d+δ)(d+d1+γ1)(1-R1)+(d+δ)(d+γ2)(1-R2)+(d+γ2)(d+d1+γ1)
a3=(d+δ)(d+d1+γ1)(d+γ2)(1-R0)
根據Routh-Hurwitz判據,有
H1=a1>0
H2=a1a2-a3=[(d+δ)2(d+d1+γ1)+(d+δ)(d+d1+γ1)2](1-R1)+
[(d+δ)2(d+γ2)+(d+δ)(d+γ2)2](1-R2)+(d+γ2)(d+d1+γ1)2+
(d+γ2)2(d+d1+γ1)+2(d+δ)(d+d1+γ1)(d+γ2)
H3=a3H2
當R0<1時,ai>0,i=1,2,3,Hj>0,j=1,2,3,即系統(1)的無病平衡點P0在Ω內是局部漸近穩定的。
定理3當R0<1時,系統(1)的無病平衡點P0在Ω內是全局漸近穩定的。
證明構造Lyapunov函數:
V=B1E+B2I+B3A
式中:Bi,i=1,2,3表示未知的正數。
計算V沿著系統(1)的導數,可得
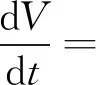
B1[β1I+β2A-(d+δ)E]+B2[τδE-(d+d1+γ1)I]+B3[(1-τ)δE-(d+γ2)A]=
[B1β1-B2(d+d1+γ1)]I+[B1β2-B3(d+γ2)]A+[B2τδ-B1(d+δ)+B3(1-τ)δ]E=
令
則有
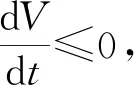
定理4當R0>1時,系統(1)的地方病平衡點P*在Ω內是局部漸近穩定的。
證明使用中心流形理論[17]來證明P*的局部漸近穩定性。
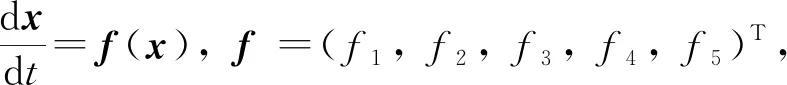

系統(1)在P0處的Jacobi矩陣為:
當R0=1時,選擇β2作為分支參數,則有
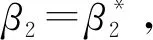
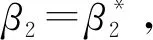
計算得
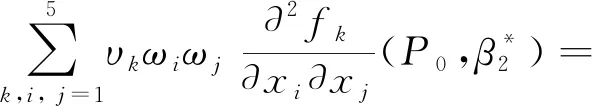
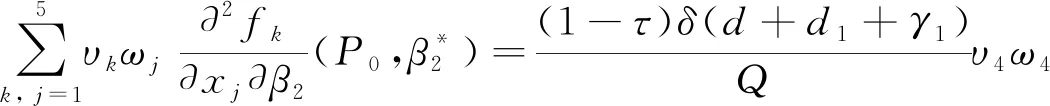

4 數值模擬
為驗證以上結果,使用Matlab對系統(1)的結論進行數值模擬,驗證無病平衡點和地方病平衡點的穩定性,研究不同參數對R0和感染者的影響,具體情況如下:
圖1模擬了無病平衡點的穩定性,取參數Λ=0.25,d=0.08,d1=0.002,γ1=0.7,γ2=0.2,β1=0.4,β2=0.3。圖1(a)取δ=0.2,τ=0.4,此時R0=0.605 3<1,可以看出無病平衡點P0在Ω內是全局漸近穩定的。通過追蹤并隔離密切接觸者可以極大減少疾病傳播,從而減小潛伏者到染病者的轉移率δ,通過核酸檢測可以及早發現無癥狀感染者,從而增加潛伏者轉移為有癥狀感染者的比例τ。圖1(b)取δ=0.02,τ=0.9,此時R0=0.054 3<1,可以看出無癥狀感染者和有癥狀感染者趨于消亡的時間明顯縮短。
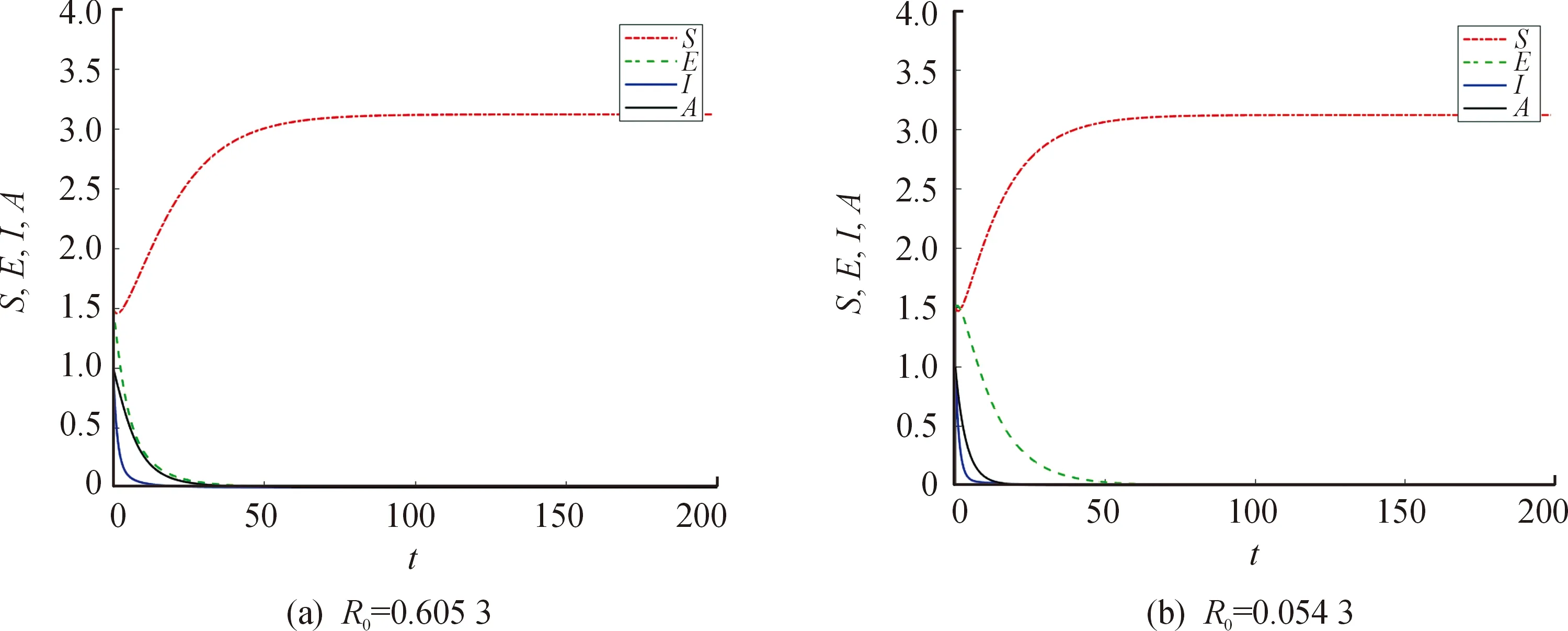
圖1 無病平衡點的穩定性
圖2模擬了地方病平衡點的穩定性,取參數Λ=0.25,d=0.08,γ1=0.7,γ2=0.2,β1=0.6,β2=0.5,d1=0.002。圖2(a)取δ=0.2,τ=0.4,,此時R0=2.124 6>1,可以看出地方病平衡點P*在Ω內是局部漸近穩定的。同樣,通過改變δ和τ,來探討追蹤密切接觸者和核酸檢測對COVID-19傳播的影響效果。圖2(b)取δ=0.1,τ=0.5,此時R0=1.358 9>1,同樣可以看出無癥狀感染者和有癥狀感染者趨于穩定的時間明顯縮短。由圖1和圖2可以看出,通過追蹤隔離密切接觸者并對易感人群進行核酸檢測來尋找無癥狀感染者,可以明顯縮短疾病消亡和趨于穩定的時間,進而有效控制COVID-19的傳播。
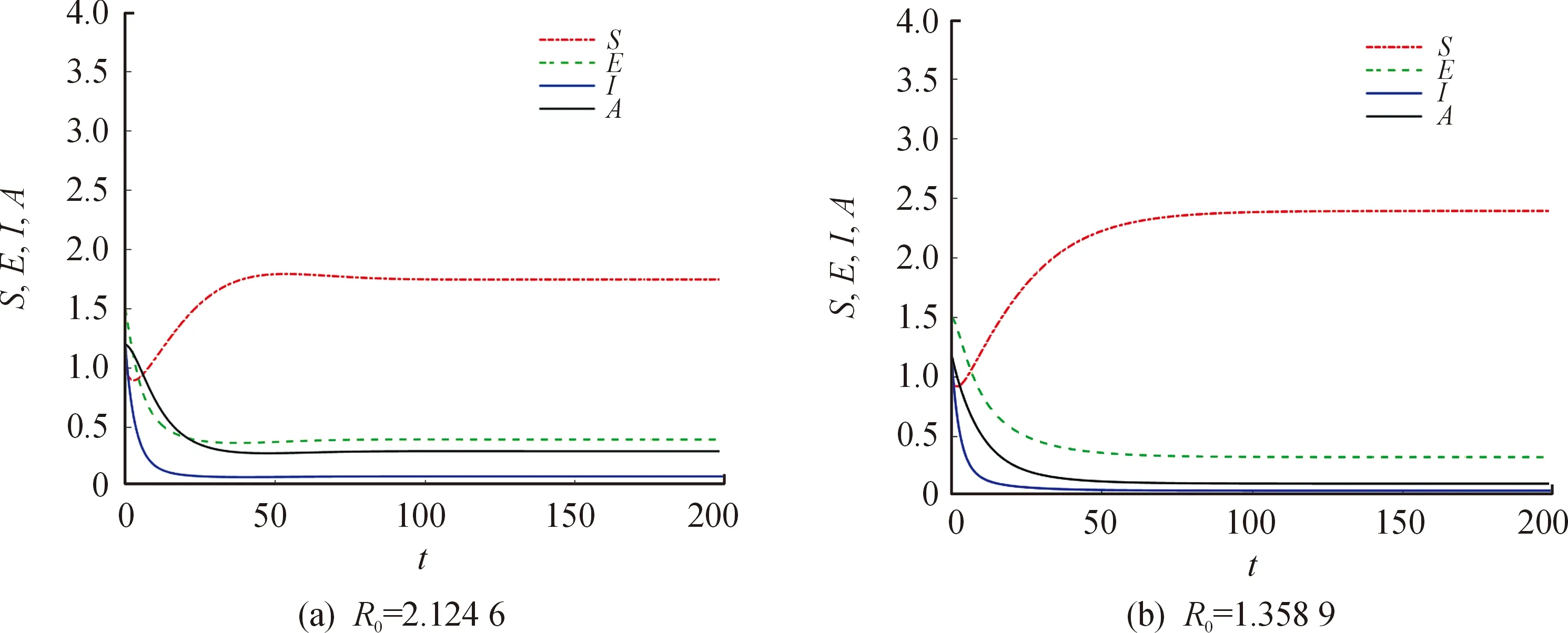
圖2 地方病平衡點的穩定性
圖3模擬了有效接觸率β1和β2取不同值時對總感染人數I(t)+A(t)的影響,取與圖1(a)相同的參數。圖3(a)中β1分別取0.9、0.6、0.3、0.1,分析了輕度社交距離(β1=0.9)、中度社交距離(β1降低到0.6)、相對嚴格的社交距離(β1降低到0.3)和非常嚴格的社交距離(β1降低到0.1)對疾病傳播的影響。從圖3(a)可以看出,加強社交距離可以顯著降低總感染人數和疾病消亡的時間。因此,政府應該實施嚴格的社交距離措施,減少人與人之間的接觸,呼吁大家外出要戴口罩并保持2 m或2 m以上的距離。圖3(b)中β2分別取0.5、0.4、0.3、0.1,可以看出減少有效接觸率β2,總感染人數顯著減少,疾病消亡的時間明顯縮短。這表明,無癥狀感染者正在嚴重加重疾病負擔,因此,所有密切接觸者一定要及時做核酸檢測并隔離14天以上。

圖3 有效接觸率β1和β2對總感染人數的影響
5 結論
研究了一類包含無癥狀和有癥狀感染的COVID-19模型,考慮了非藥物干預措施對傳染病傳播的影響。計算了基本再生數R0,并證明了地方病平衡點的存在性,運用Routh-Hurwitz判據和LaSalle不變集原理,證明了當R0<1時,無病平衡點P0是局部漸近穩定和全局漸近穩定的;運用中心流形理論,證明了當R0>1時,地方病平衡點P*是局部漸近穩定的。最后通過數值模擬對結論進行驗證,結果顯示,實施非藥物干預措施將顯著減少累積的感染病例。因此,在防疫期間,應嚴格執行基本的非藥物干預措施,特別是保持社交距離和及時追蹤隔離密切接觸者,以減少疾病傳播。

