基于雙層規劃的老城區自行車專用道網絡設計
王 豐,劉昊翔,2
(1.合肥工業大學,汽車與交通工程學院,合肥 230009;2.合肥工業大學,安徽省智慧交通車路協同工程研究中心,合肥 230009)
0 引 言
隨著社會經濟的迅速發展,私家車的保有量逐年增加,老舊城區的交通擁堵問題變得日益嚴重。尤其是老城區人口居住量大,有大量的短距離出行需求,比如,出門買菜、接送小孩、“最后一公里”等。國內大部分城市的老城區由于歷史和經濟原因,道路狹窄且密集,且部分特殊區域,如城中村、傳統老街等,由于道路空間的限制,公共交通站點覆蓋率較低,導致有限的道路供給無法滿足大量的出行需求,很容易造成老城區機非車流混合且極易擁堵的交通狀況。已有研究表明[1-3],在老城區中合理地規劃自行車路網,可以提高自行車出行的分擔率,同時能減少機動車出行,從而有效地緩解交通擁堵。如何在老城區合理地規劃自行車專用設施,是政府部門進行交通規劃的難題。
自行車作為一種慢行交通方式,其基礎配套設施的規劃是城市交通規劃領域的重要組成部分,2017 年,劉蘭輝等人[4]基于上海南匯新城自行車交通流和自行車道路設施的現場調查和分析,從路網連續性、路面平整度等角度提出了完善自行車交通設施的措施與建議。2018年,李翔[5]提出了由以“車”為本到以“人”為本的理念,并基于這種理念對廣州市自行車交通相關的道路規劃和設計提出優化建議。2019年,許珂源等人[6]在研究慢行交通中提出在中心城區通過修建自行車專用道可以提供更加便利和綠色的出行方式,自行車可被作為短途通勤和多種出行方式間接駁的重要出行方式之一。楊永平和陳春羽[7]分析了國內外自行車發展及趨勢,提出了自行車專用路的設計要點,為后續自行車專用路的發展提供了參考。2020年,黃玥和干宏程[8]從自行車出行路徑選擇行為影響因素、模型方法、實驗調查方法以及應用場景等方面系統梳理了自行車出行路徑選擇偏好的研究成果。許乃星和陳亮[9]深入分析自行車專用路的網絡分級、規劃原則、設置形式、寬度與坡度、節點通過方式、出入口與銜接、服務配套等建設技術指標,為自行車專用路規劃與建設提供了指導。以上以慢行交通為背景的研究主要從定性研究的角度,從車道寬度、路面平整度、機非隔離帶、自行車道的連通性等方面分析了自行車基礎配套設施的合理度,并結合實際提出了優化建議。
除了定性研究以外,也有學者從定量的數學建模角度對自行車網絡設計問題進行了分析研究。2017 年,宋青等人[10]在對真實騎行者路徑選擇行為深入分析的基礎上,提出了基于Open Street Map 的城市自行車網絡的構建方法及基于其上的多判據自行車路徑優化的數學模型,并給出了求解該模型的一種基于聚類的最優多判據路徑規劃方法。Mauttone[11]等人以最小化用戶和規劃者的費用為目標函數,建立了一個混合整數規劃模型,并設計了一個遺傳算法對模型進行求解,采用算例分析驗證了算法和模型的有效性。2018年,Chen[12]采用網絡流技術和數學規劃方法,針對現有的自行車網絡系統,構建了自行車網絡設計模型。該模型的目標是在滿足相關運營約束的前提下,使騎自行車者的出行時間最小化,將提出的模型表述為混合整數多商品網絡流問題,還提出了一種高效的算法以求解提出的大規模現實問題模型,測試結果表明所提模型和求解算法的有效性。2019 年,Shui 和Chan[13]以最小化所有出行者的出行時間為目標函數,考慮投資預算約束和覆蓋所有出行點的約束,建立了一個優化數學模型,并結合遺傳算法和兩階段求解方法對問題進行求解。Zuo和Wei[14]考慮自行車的連通性和對其他出行的影響,以最小化系統總阻抗為目標,采用多準則決策分析方法對路網進行決策,算例分析表明該方法能提高出行者選擇自行車出行的比率。Liu等[15]建立了一個基于隨機用戶均衡的自行車網絡設計雙層規劃模型,以最大化系統總效益為目標,考慮投資預算約束建立了數學模型,并通過對數學模型的線性化處理,提出了一個基于混合整數線性規劃的全局優化算法,以及一個基于代理模型的全局優化數學啟發式算法對問題進行有效求解。2020 年,He 等人[16]基于GPS 提供的共享單車騎行軌跡數據,考慮投資預算、道路長度、效益最大化這三個約束條件,以自行車道的覆蓋范圍最大化為目標函數建立數學優化模型,旨在為政府提供自行車道的規劃方案,并采用貪婪啟發式算法對問題進行求解,算例分析結果表明了算法和模型的有效性。Zhu 等人[17]基于時空可達性約束,考慮可達性、建設成本、出行者出行成本預算、交叉點個數等因素,建立了多目標優化數學模型,并遵循兩階段原則設計一個啟發式算法對問題進行求解。2021 年,Oliveira 等人[18]綜合考慮車道舒適度、安全性、路徑客觀性、網絡連接性、投資預算,利用網絡多目標優化和混合整數線性規劃的概念,建立自行車專用道網絡設計的數學模型,并實現最優策略的求解,結果分析表明自行車專用道的建立可以有效促進自行車替代部分機動車出行。
以上定量研究皆是通過建立最優化數學模型來描述自行車專用道網絡設計問題,優化目標包括最小化系統總成本、出行阻抗、投資預算、連通性、多目標優化等,并針對不同的建模方式和問題背景設計不同的求解算法。但是以上眾多研究中,還沒有學者針對老城區的道路現狀,考慮出行者的選擇行為提出自行車專用道的設計方法。一般來說,基于雙層規劃的方法建立數學模型可以在下層模型中考慮出行者的出行選擇行為,因此可以更加準確地描述交通系統中出行者與決策部門之間的相互關系。許多學者研究了基于雙層規劃的交通網絡設計問題[19-20],并在最優定價、公交排班、多目標優化等[21-22]領域取得廣泛的應用。
本文在當前的自行車網絡設計研究基礎上,結合國內城市老城區中短距離出行需求多、道路密、機非混合等特點,考慮到自行車的出行特性可很好地契合老城區的交通環境,有效緩解老城區的交通擁堵的特點,提出一個新的自行車網絡設計問題。即采用新建自行車專用道和禁行機動車的方式構建連通的自行車交通網絡,目標是提供更為便利的自行車基礎設施,以達到促進自行車出行和緩解交通擁堵的目的。建立了雙層規劃模型描述該問題,上層模型為連通性約束下的決策模型,目標函數為最小化系統總建設成本,下層模型為描述出行者彈性需求的Logit 模型和自行車、機動車的UE 交通分配模型。提出了改進的遺傳算法對該雙層規劃模型進行求解,并在遺傳算法中嵌入了自適應平均算法(SRAM)[23]和Frank-Wolfe[24]算法,分別求解Logit 模型和UE 交通分配模型。算例部分對所提出模型和算法的可行性和有效性進行了分析說明。
與已有研究相比,本文的研究貢獻如下:
(1)采用新建自行車專用道和利用現有的道路禁行機動車的方式構建自行車網絡,并增加自行車網絡連通性的約束,可以最大程度地保證自行車出行的便利性和安全性。
(2)所提出的模型中考慮了需求彈性和路徑選擇,比采用固定需求可以更好地緩解交通擁堵問題。
(3)提出一個改進的遺傳算法求解雙層規劃模型,并嵌入Frank-Wolfe 算法和SRAM 算法有效地求解下層問題。
1 數學建模
政府主導自行車基礎設施網絡的規劃,根據OD 需求和交通網絡現狀,決策在現有道路網絡上如何構建連通的自行車專用道網絡,降低系統的交通出行總費用。自行車專用道改造方案主要有兩種:一是在道路空間足夠的路段上,花費資金建設新的道路作為自行車專用道;二是在道路空間狹小,且平行路段較多的路段上,對機動車道路采取機動車禁行措施。改造目標旨在最小化系統總成本情況下,構建一個連通的自行車專用道網絡。即從所有OD 對的起訖點集合中任一點出發均可通過自行車專用道到達起訖點中另一任意點。出行者會隨著道路網上的自行車專用道修建情況和OD 對之間阻抗的變化而改變出行模式和路徑選擇,即考慮選擇使用機動車或者自行車出行,并決策所使用的路徑。由此可見,政府的決策方案將影響出行者的出行模式和路徑選擇,而出行者的出行行為也會反過來影響政府決策。因此,本文所提出的問題可以構建為一個雙層規劃模型,其框架結構如圖1所示。
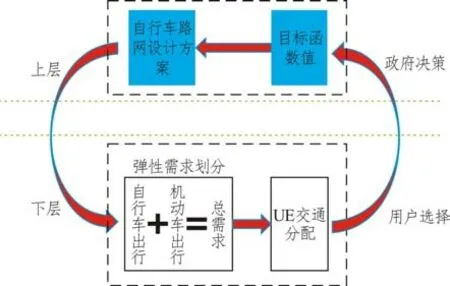
圖1 雙層規劃模型框架圖Fig.1 Framework of the bi-lever programming model
為了便于建模和理解做出如下假設:(1)OD對之間總出行需求已知且恒定,自行車與機動車出行需求之間存在彈性;(2)道路類型改變后,OD間的總出行需求不變;(3)自行車與機動車分別只能在自行車專用道與機動車道上行駛;(4)不考慮其他類型車輛對自行車和機動車的影響。
本文符號定義如表1所示。

表1 參數及變量含義Tab.1 Definition of parameters and variables

續表1
1.1 上層自行車專用道規劃模型
上層自行車專用道規劃模型站在政府管理者的角度,以系統總費用最小為目標函數,以自行車網絡連通性為主要約束條件,其數學模型如下:

模型中目標函數(1)旨在最小化系統總費用,其中第一項是自行車專用道的建設費用,第二項是機動車和自行車的出行總阻抗,σ是出行者的時間價值系數。約束(2)表示路段a上新建自行車專用道和禁行機動車策略只能采用其一。約束(3)和(4)均表示從所有的OD 對起訖點集合中任選兩個點r和e,在r、e之間均存在連通的自行車專用道相連。最終的決策方案中,所有起訖點的任意兩點之間都可以通過自行車專用道相連,這符合連通網絡的定義。約束(4)表示連接r、e之間的自行車可行路徑上的路段均為自行車專用道,即zrea=1 的前提條件是xa=1 或者ya=1。換句話說,該路段如果是自行車專用道,那么表示新建了自行車專用道,或者采取了機動車禁行措施。約束(5)表示xa、ya、zrea均是0-1變量。
1.2 下層需求方式劃分和交通分配模型
考慮到老城區短距離出行需求多,道路空間狹小,公共交通覆蓋率不高等情況,故在本文研究中簡單地將所有的機動車都視作小汽車處理,模型下層只考慮自行車和小汽車的出行模式。給定一個可行的自行車專用道網絡設計方案,在OD 總需求已知的情況下,下層模型可以預測出行者對自行車和小汽車出行模式的選擇,進而預測小汽車網絡和自行車網絡各自的流量分配。假設用戶對小汽車出行和自行車出行方式的選擇服從Logit 模型,而用戶的出行路徑選擇服從UE 均衡準則,則下層的用戶出行行為模型如下所示。
(1)需求劃分模型:
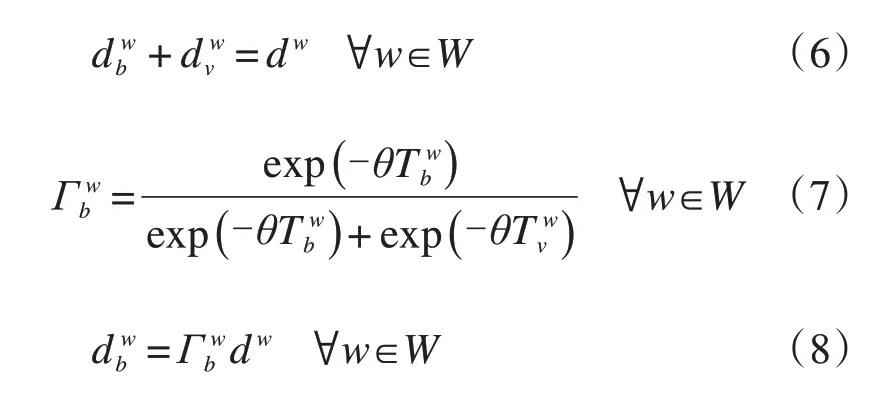
約束(6)表示選擇機動車和自行車的出行者總和等于OD 對之間總需求;約束(7)用Logit 模型描述出行者選擇自行車出行的概率;約束(8)表示OD 對w之間的自行車出行需求。
(2)自行車的UE交通分配模型:
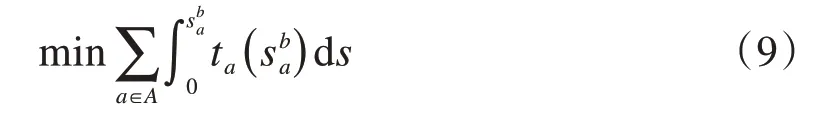
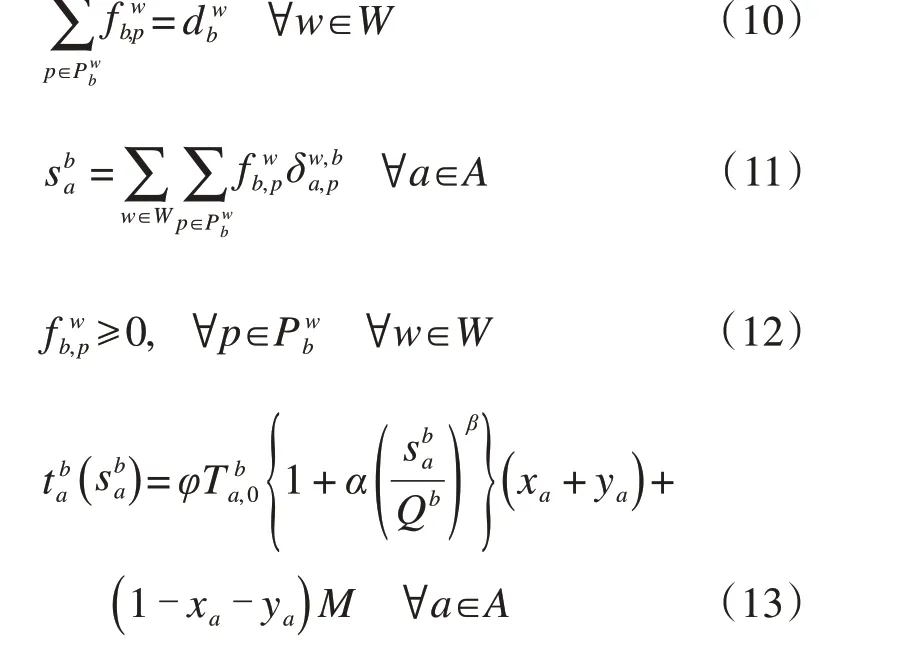
約束(10)表示OD 對之間總需求與各路徑流量的守恒關系;約束(11)表示自行車路段流量和路徑流量的關系;約束(12)限制了各自行車路徑流量都為非負。
在UE 交通分配問題中,我們采用了基于美國聯邦公路局(Bureau of public road,BPR)開發的阻抗函數,即BPR[25]函數來描述路段阻抗,其中α和β為模型參數,分別取值0.15 和4。根據已有涉及自行車阻抗的研究,本文為了使自行車的阻抗更加符合實際情況,在BPR 函數中加入了自行車阻抗系數φ(0<φ<1),并且在3.4 小節中對該系數的影響做了分析說明。約束(13)表示自行車阻抗計算公式,xa=1 或者ya=1 表示路段a上有自行車專用道自行車可以通行,否則表示路段上無自行車專用道,自行車無法通行,通行時間為無窮大。
(3)機動車的UE交通分配模型:
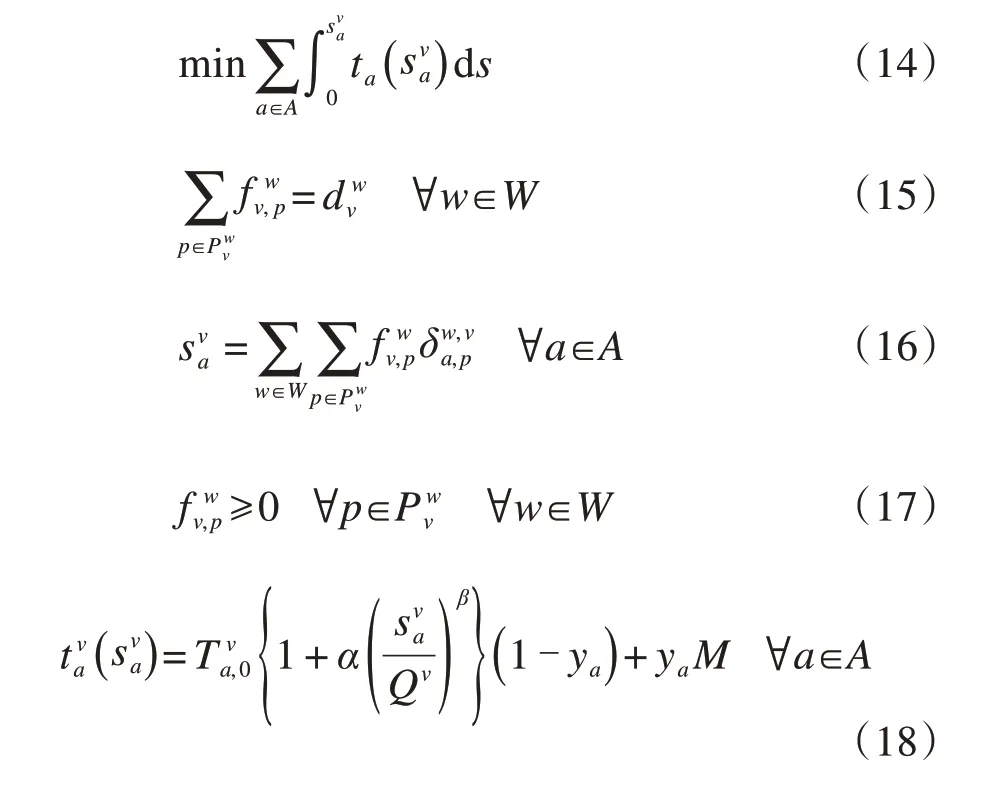
機動車的UE 交通分配模型(14)~(18)與自行車出行類似。在約束(18)中,ya=1 表示路段a被禁行,則該路段上機動車的走行時間為無窮大;ya=0 表示未禁行,則采用標準的BPR 函數計算機動車的路段走行時間。
2 求解算法
由于雙層規劃模型是一個NP-hard 問題[26],許多學者從求解算法方面對該類模型進行了大量研究[27-33]。本文所提出模型帶有連通性的約束條件,并且下層問題包含模式劃分和交通分配模型,因此為了有效求解該模型,采用基于遺傳算法(Genetic Algorithm, GA)[34]的求解算法框架,并提出檢查和更新網絡連通性的策略,對下層的Logit模型和UE 交通分配分別采用自適應平均算法(SRAM)及Frank-Wolfe算法進行有效求解。
本文所提出的基于GA 的算法框架如圖2 所示,其中嵌入的SRAM 算法和Frank-Wolfe 算法具體流程分別在后面2.2 和2.3 中進行敘述。
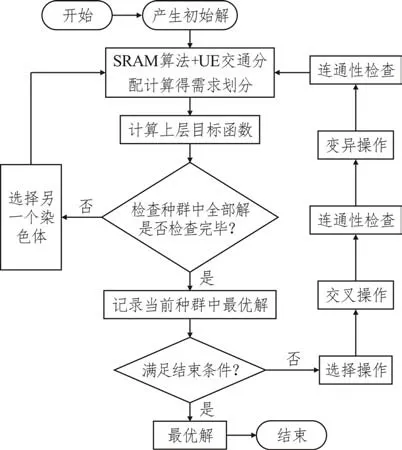
圖2 算法框架Fig.2 Algorithm framework
遺傳算法求解網絡設計:

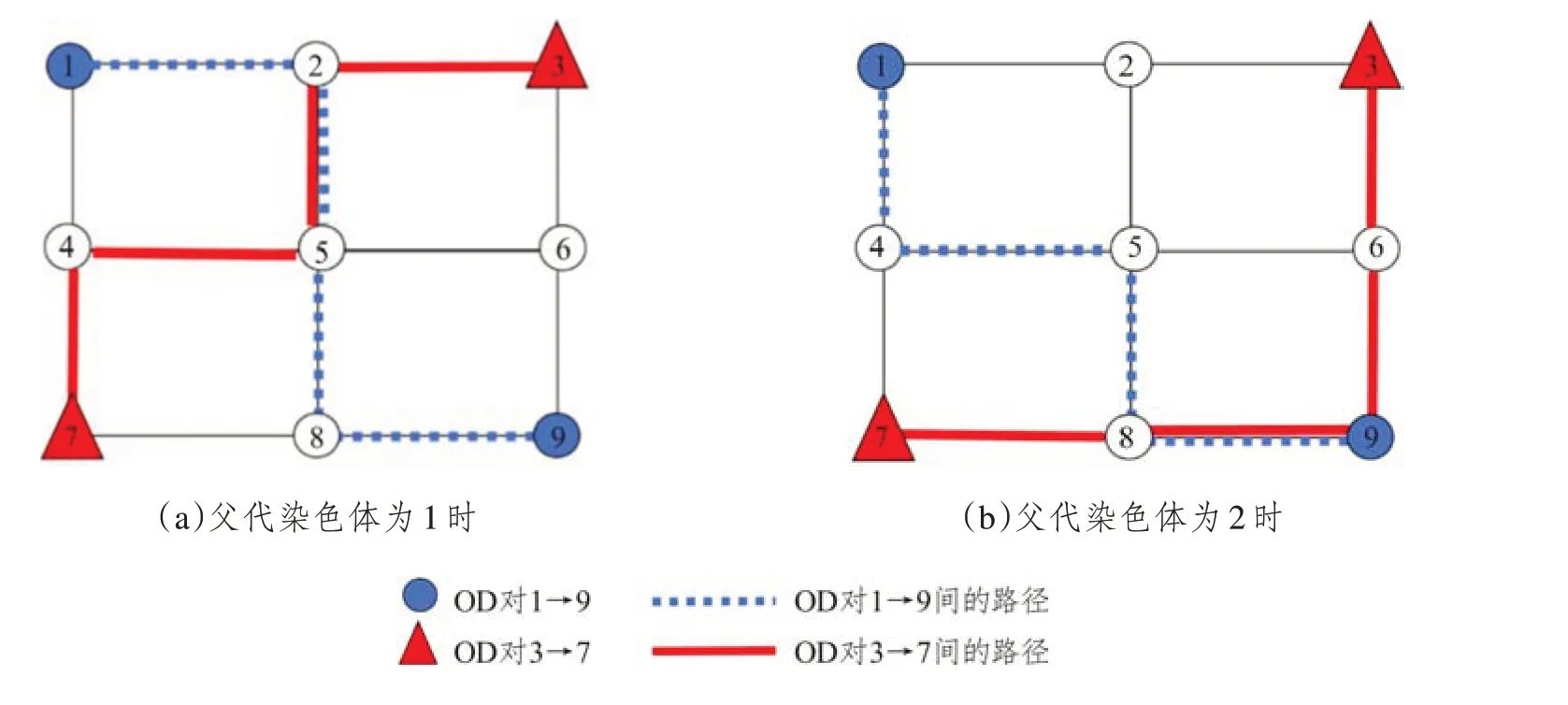
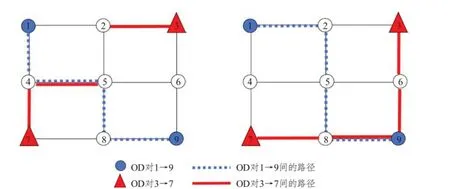
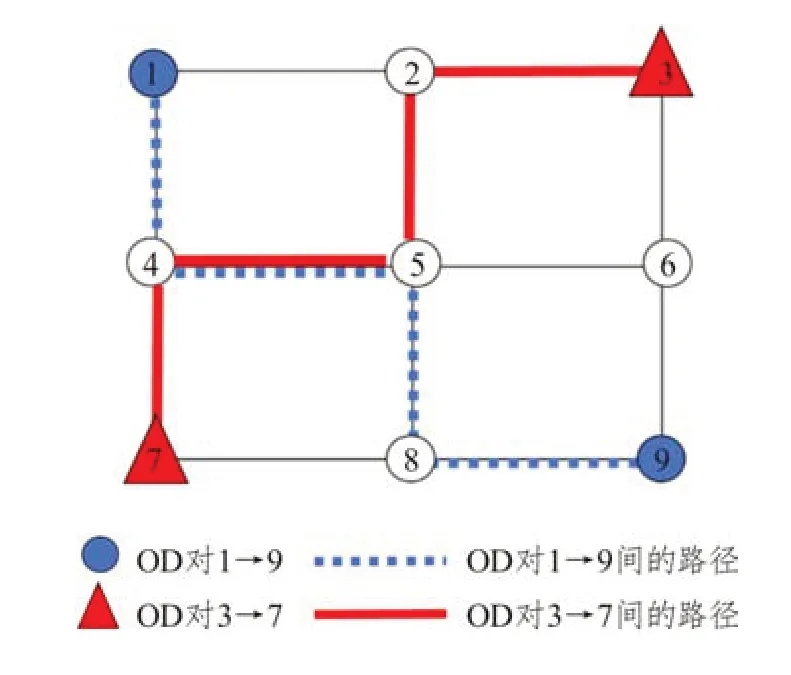
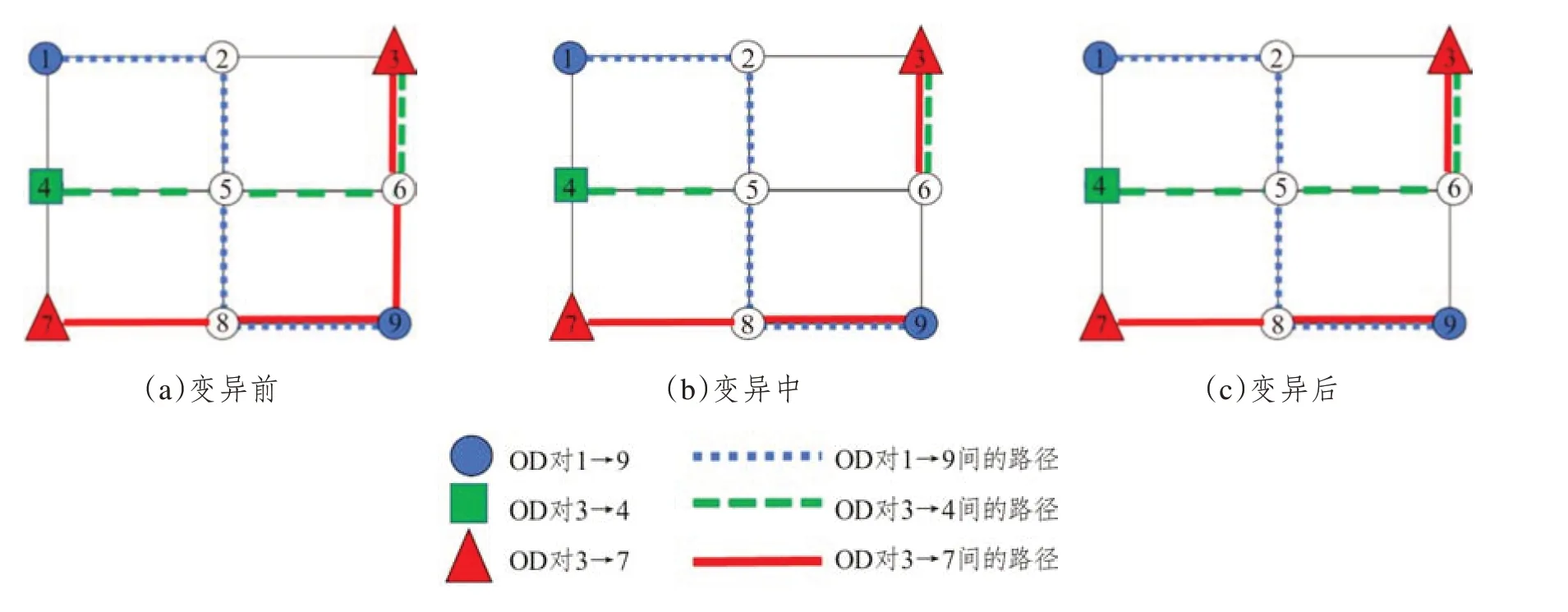
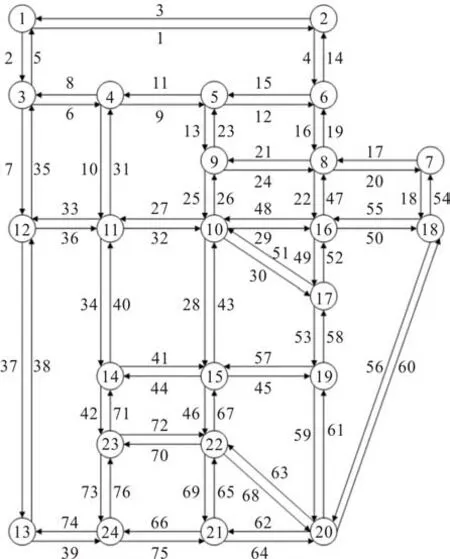
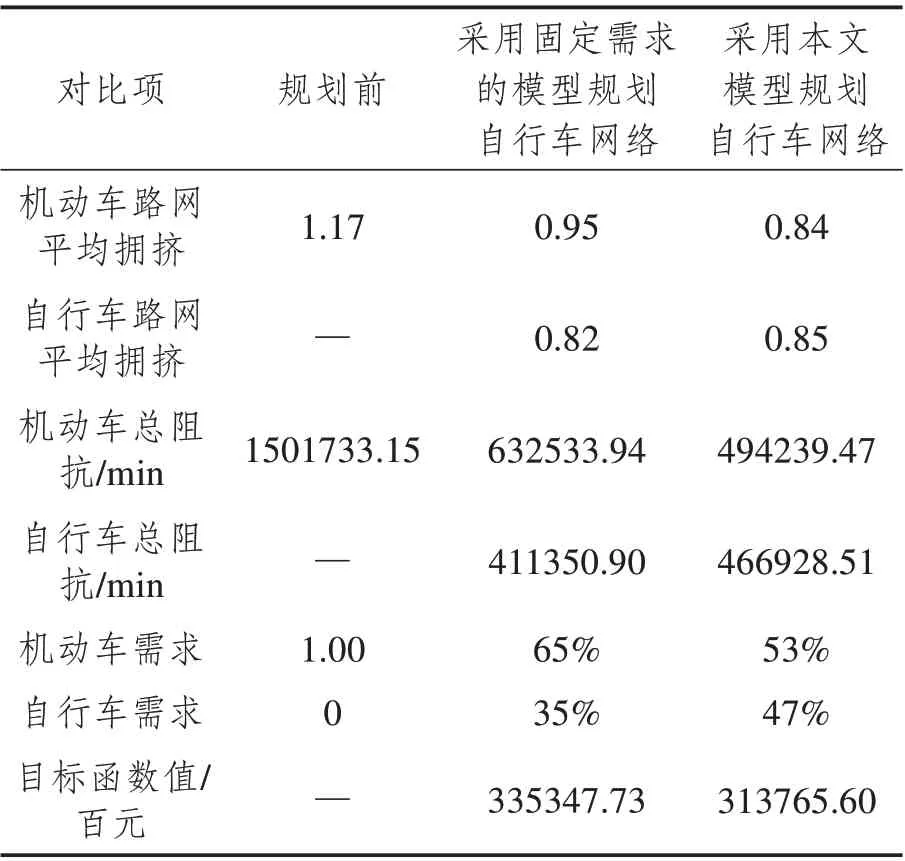
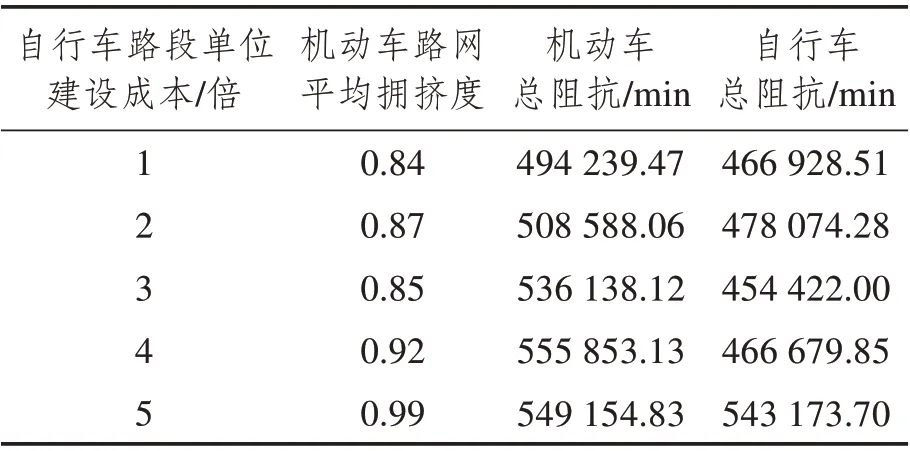
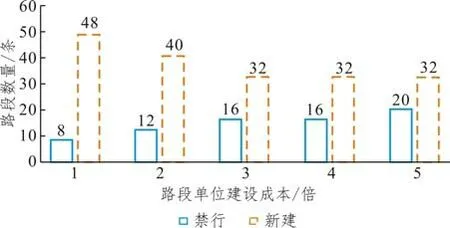
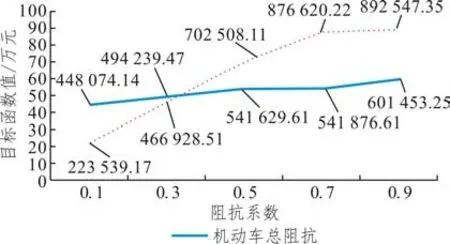
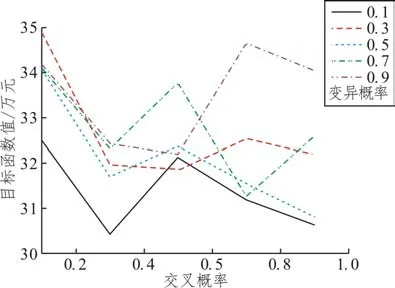
輸入:種群規模m、交叉概率pc、變異概率pm、最大迭代次數kmax生成m個初始解(染色體)構成初始種群Φˉ0,初始化迭代次數k = 0用SRAM算法分別對種群Φˉ0中所有個體求解,得到每個個體的目標函數值,可根據目標函數值計算適應度,并置ubest為Φˉ0中的最優解。根據輪盤賭原則按照適應度大小從Φˉ0中挑選出m個個體得到新的一組解Φ0 While k 遺傳算法是通過模擬達爾文生物進化論的自然選擇和遺傳學機理的生物進化過程搜索最優解。從一個初代種群開始,按照適者生存和優勝劣汰的原理,根據個體的適應度選擇個體進行組合交叉和變異,逐代演化產生出越來越好的解。遺傳算法中的種群由多個個體,即染色體組成,每個染色體由一組基因構成。在本文中,每個染色體代表模型的一個解,即自行車的網絡設計方案。染色體上的基因表示解中每個路段是否有專用道,是新建專用道還是禁行小汽車,本文中基因的取值有0、1、2三種情況,0表示小汽車禁行(相當于ya= 1),1表示新建自行車專用道(相當于xa= 1),2 表示仍是小汽車道(相當于xa+ya=0)。例如,圖3給出了一個有15個基因的染色體,該染色體共有6 條路段為新建專用道,4 條路段為小汽車禁行,5條路段仍是小汽車專用道。 圖3 染色體示例Fig.3 Chromosome example 2.1.1 解的初始化 在遺傳算法開始時,首先要產生一組種群大小為K的初始解,即K個連通的自行車專用道設計方案,其中,每個可行解均由以下兩個步驟產生。 首先,產生連通的自行車基礎網絡。為了便于描述,將給定的m個OD 對標上序號,即第一對OD對為O1D1,第二對為O2D2,…,第m對為OmDm。從第一個起點O1中找到一條連到終點D1的路徑,該路徑為當前小汽車最短路或者次短路,當O1D1間有大于2條以上路徑時,則隨機采用最短路或者次短路。然后再從已連接專用道的節點中選一個點J,使J離下一個起點O2最近,找到J到起點O2的最短路徑,再從起點O2按照同樣的方法找一條連到終點D2的路徑,接下來再去連接第三個起點O3,從O3連到D3后,再去連第4個起點O4……這樣循環直到把所有的OD對都覆蓋到。這樣即得到了一個所有點都是連通的且OD對之間也是連通的一個解。 其次,在當前連通的路網上,設置自行車專用道和禁行路段。設置初始概率P0,針對上一步產生的路網當中的每一個路段a隨機產生一個概率pa,若pa>P0,則該路段采用禁行措施,否則新建自行車專用道。 執行以上兩個步驟可以得到一組可行解。再從所有OD 對的起點中選O2O2作為起點,分別找到O2D2的路徑再連到O3,找到O3D3的路徑連到O4…找到OmDm的路徑,連到O1,這可以得到另一組可行解。重復執行同樣的操作,直到得到K個初始可行解。 圖4 演示了有3個OD 對需求的初始解生成過程,圖中所有路段皆可通行。給三個OD 對隨機排序:O1D1為1→9(藍色)、O2D2為2→8(綠色)、O3D3為3→7(紅色),如圖4(a)所示。首先,要找O1到D1的連通路徑,采用最短路和次短路的方法可以找到O1到D1間有兩條路徑,假設隨機選用了次短路,該路徑為1→4→5→8→9,如圖4(b)所示。其次,找到1、4、5、8、9 節點中距第二個OD 對的起點2 最近的點,假設這個點是5,則連接5→2 之間的最短路徑,如圖4(c)所示;再按照最短路和次短路的方法找到OD 對2→8 之間的路徑,假設隨機選取了2→8 間的最短路,該路徑為2→5→8,如圖4(d)所示。此時已連接專用道的節點有1、2、4、5、8、9,再從這些節點中找到離第三個OD對的起點3最近的點,假設找到的這個點為2,則連接2→3 之間的最短路徑,如圖4(e)所示;再按照最短路和次短路的方法找到OD 對3→7 之間的路徑,假設隨機選取了3→7 間的最短路,該路徑為3→2→5→8→7,如圖4(f)所示。注,圖中某些節點之間有多條不同顏色的路徑,如圖4(f)中的2→5節點間,有三種不同的顏色,這表示該路段上只有一條自行車專用道,這條自行車專用道被多個OD 對同時使用,而不是在這個路段上修建了多條自行車專用道。 完成以上步驟后可得到一個滿足連通性條件的自行車道網絡,再對連通網絡上的每一個路段a按照隨機概率的方式,即可確定每個路段是采用新建自行車專用道還是禁行機動車道,至此可以得到一個完整可行的自行車專用道網絡作為第一個初始解。按照同樣的方式,從第二個OD 對的起點開始執行操作,可以得到第二個初始解,重復以上操作,直到得到K個初始解。 2.1.2 選擇操作 在遺傳算法的迭代過程中,每計算完一組解的目標函數值后,需要通過選擇操作,從當前這組解中選出一組新的解。本文采用輪盤賭的方法,以每個解的目標函數的倒數作為適應度,這樣目標函數值較小的解被選中的概率更大,可以保證更優的解被選中加入到下一代種群中。以Sr表示每個解被選中的概率,Or表示每個解的目標函數值,m表示種群的規模,即解的數量,則Sr可表示如下: 2.1.3 交叉操作 為了保證解的收斂速度更快以及不陷入局部最優解,在選擇操作結束后,需要對得到的染色體分別進行交叉操作。針對本文所提出的模型設計了一個最短路交叉算子:在兩個父代染色體φ1、φ2中任選一個相同的OD 對,分別找到兩個染色體中該OD對之間的自行車最短路徑pwφ1、pwφ2,然后交換兩個最短路徑中的路段所對應的解的片段,這樣即得到兩個新的染色體;在K個解的交叉操作中,分別選取第1個解與第2個解交叉,第3個解與第4個解交叉……第K個解與第1個解交叉。 圖5和圖6以一個9節點網絡為例說明了最短路交叉算子的具體執行過程。該9 節點網絡包含兩個OD 對,分別是1→9 和3→7,其中藍線和紅線表示連通各OD 對的自行車專用道路徑(包括新建專用道和機動車禁行道路),其余黑線表示機動車道。圖5 中(a)、(b)兩圖分別表示兩個不同的解,左邊表示父代染色體為1 時,右邊表示父代染色體為2 時。在父代染色體1 中,OD 對1→9 之間的路徑為1→2→5→8→9,OD 對3→7 之間的路徑為3→2→5→4→7;在父代染色體2 中,OD 對1→9 之間的路徑為1→4→5→8→9,OD 對3→7 之間的路徑為3→6→9→8→7。選取OD 對1→9 為例,交換其自行車最短路徑所包含的路段對應的解的片段,即將父代染色體1 中藍線與父代染色體2 中藍線交換可得圖6所示的子代染色體。注意,圖6(a)在交叉算子執行后產生了不連通的自行車專用道網絡。 圖5 父代染色體圖Fig.5 Parent chromosomes 圖6 子代染色體圖Fig.6 Children chromosomes 2.1.4 檢查和修正操作 為了保證解的可行性,在交叉算子執行后,必須檢查每個染色體的自行車網絡連通性,以保證解的可行性。因此,設計了相應的連通性檢查和修正算子如下:按照OD 對順序,檢查每一個OD 對的起點是否能連通到網絡上OD 對起訖點中的任意點,若所有起點均能連通到其他點,則該網絡滿足連通性約束;否則找到這個不連通的點,并找到與不連通點相連的自行車專用道中離起點最近的節點,將該節點與起點用自行車專用道連接起來,專用道隨機采用禁行或者新建的策略,再從每一個OD 對的起點開始檢查,直到網絡連通。 以圖6 為例檢查網絡連通性。首先以子代染色體2 為例,從第一個OD 對的起點1 開始檢查,1可以連接到點3、7、9;再以第二個OD 對的起點3開始檢查,3 可以連接到1、7、9。檢查完所有OD對的起點,每個起點均連通,因此該自行車網絡滿足連通性要求。 再以子代染色體1 為例,從第一個OD 對起點1 開始檢查,1 連接不到3,因此找到與3 相連的某一點D′,與起點1 相連的某一點O′,使O′→D′距離最短。以圖6 為例假設D′為2,O′為5,則將2→5用自行車專用道連接起來,連通性修正后如圖7所示,此時1—3 之間則滿足連通性的要求。為了保證其他點也完全相連,每檢查并更新一次連通性后,需要再次按照OD 對順序的起點開始檢查。因此再次從第一個OD 對起點1 開始檢查,1 可以連接到3、7、9;再檢查第二個OD 對起點3,3 可以連接到1、7、9。此時檢查完畢,整個自行車專用道設計滿足連通性要求,則父代兩條染色體經過交叉后得到滿足連通性條件的子代染色體1和2。 圖7 連通的子代染色體Fig.7 Connected children chromosome 2.1.5 變異操作 變異操作可以產生新的基因,擴大解的搜索范圍,有助于避免陷入局部最優解。考慮到交叉操作后得到的部分解中會存在冗余的自行車專用道,因此本文提出了兩種變異算子。變異算子(1):在當前染色體中,隨機找一個OD 對,檢查該OD 對之間是否存在2 條以上的自行車專用道路徑,若有則更改次短路上的所有路段為機動車道,具體更改方式如圖8的描述所示,次短路由K短路的方法產生,然后檢查和更新自行車專用道網絡的連通性,方法與2.1.4 所述相同;若無則在該OD對之間執行變異算子(2)。變異算子(2):設定一個初始概率P0,在當前染色體中隨機選擇一個OD對之間的最短自行車專用道路徑。在當前路徑的每條路段上,對每一條路段a產生一個0-1 之間的隨機數pa,若pa>P0,則當前路段發生變異。變異規則為:若當前路段為新建自行車道,則改為禁行;若當前路段為禁行,則改為新建自行車道。該算子的設計方式不僅可以保證解的可行性,還可以更大程度地減少一些不必要的自行車道,從而可以減少建設成本和提高機動車的通行效率。 圖8展示了變異算子(1)的執行過程。該道路網絡上有3 個OD 對,分別是1→9、3→4、3→7。假設當前變異找到的OD對為1→9,變異前如圖8(a)所示。可知1→9有兩條路徑分別是最短路1→2→5→8→9 和次短路1→2→5→6→9。因此,將1→2→5→6→9 從自行車網絡上刪去,因為1→2→5 也包含于路徑1→2→5→8→9中,因此僅刪除5→6→9 即可,然后得到圖8(b)。再采用2.1.4 中檢查和更新網絡連通性的方法,可得到變異后最終的結果,如圖8(c)所示。 圖8 變異前、變異中、變異后的道路網絡Fig.8 Road networks before,during and after mutation 自適應平均算法(SRAM)是經Liu等[23]改進相繼平均算法得到的求解隨機用戶均衡分配的有效算法。該算法對相繼平均算法中的迭代步長做出了改進,相比于給定的迭代步長,自適應平均算法中的迭代步長與當前解決方案和可行解決方案的距離有關。避免了相繼平均算法在迭代初期由于步長過大導致的目標函數值到一定的迭代次數后才下降的缺陷,修正了相繼平均算法在經過多次迭代后,迭代步長非常小而使得收斂速度變慢的問題。 為了得到自行車和機動車之間出行模式劃分的比例,本文采用自適應平均算法對Logit 模型進行求解。自適應平均算法主要包含兩個重要步驟:一是確定搜索下降方向與迭代步長;二是更新路段流量方案。算法計算步驟如下所示: 自行車和機動車需求分配的SRAM算法: 輸入:參數δ、γ、ε令Γ =[T w b , ?w ∈w],初始化一個分配的起始概率Γ0(本文中初始化Γ0=0.3),設置迭代次數n=1,根據Frank-Wolfe計算得到Γ1,令下降方向G0=Γ1, β0=1 While‖ ‖Gn - 1 >ε do根據Γn計算機動車和自行車的需求d nb 、d n v,然后再用Frank-Wolfe算法計算自行車與機動車各自的UE交通分配,得臨時概率Γ'n,既有下降方向Gn=Γ'n -Γn If‖ ‖Gn ≥‖ ‖Gn-1 then βn=βn-1+δ Else βn=βn-1+γ End if確定步長μn=1/βn更新Γn+1=Γn+μnGn置n=n+1 End while輸出:路段阻抗和Γn 本文將Frank-Wolfe算法嵌入自適應平均算法中分別計算自行車與小汽車各自的UE 交通分配。Frank-Wolfe 算法是Frank 和Wolfe(1956)[24]提出的求解線性約束下的非線性規劃問題的一種算法。 Frank-Wolfe 算法應用在UE 交通分配時計算流程如下: 輸入:精度ε>0基于所有路段的自由流走行時間,做全有全無交通分配,得到初始的路段流量s0,置迭代次數k = 0 while G(sk) >ε do以sk為輸入,做全有全無交通分配,得到路段流量s'k置可行下降方向dk = s'k - sk進行一維搜索得到最優步長λk更新路段流量sk + 1 = sk + λkdk置k = k + 1 end while輸出:sk 該算法在初始化過程中用最短路做全有全無交通分配的時候,自行車和小汽車路段的阻抗均采用阻抗函數中的自由流時間計算。在UE 交通分配問題的求解過程中,采用式(20)所示的間隙函數(Gap Function)來評價解的精度: 采用算例分析對提出算法和模型的準確性及有效性進行分析,以Sioux Falls 網絡為例進行測試。假設網絡上所有的路段都既可以禁行也可以新建機動車專用道,網絡包含了24 個節點和76 條路徑、20個OD對,見圖9所示。 圖9 Sioux Falls網絡Fig.9 Sioux Falls road network OD 對之間的需求如表2 所示,每條路段上機動車的自由流走行時間、路段建設費用如表3 所示。本文提出的所有算法均采用C#編程。在遺傳算法中,設置種群規模大小為70,交叉概率為0.7,變異概率為0.3,選擇第一種和第二種變異的概率都分別為0.5,在變異過程中,新建自行車道變為禁行道和禁行道變為新建自行車道的概率都分別為0.5,自行車專用道的通行能力Qb為1600,機動車道的通行能力Qv為1850,最大迭代次數通過實驗可設置為3 000 次,自行車的阻抗系數為0.3,時間價值系數為0.3,θ值為1。在SRAM 算法中,設置初始的自行車出行概率為0.3,參數δ= 1.5,γ= 0.01,ε= 0.2。 表2 各OD對之間的出行需求Tab.2 Travel demandsof different OD pairs 表3 Sioux Falls網絡中各路段信息Tab.3 Road segments information in the sioux falls network Sioux Falls 網絡求解的結果如圖10 所示,紅色的為禁行路段,藍色的為新建自行車專用道路段,包括8 條禁行道路和48 條新建自行車道。從圖10 中可以看出,自行車專用道網絡覆蓋到了OD 對所有的起訖點。 圖10 連通的自行車專用道網絡Fig.10 Connected bike network 圖11 展示了目標函數的收斂過程。遺傳算法在前1 200 次的迭代過程中,結果收斂較快,之后保持不變,最終收斂在313 765.60 百元處,整個收斂過程耗時約10 min。 圖11 目標函數收斂圖Fig.11 Objective function convergence 表4對比了自行車網絡規劃前、后路網擁擠程度和總阻抗的變化。第二列展示了自行車網絡規劃前的結果,第三列展示了考慮固定需求的模型規劃自行車網絡的結果,即各OD 對之間的出行需求是固定的,第四列展示了本文所提出模型的結果。 表4 路網擁擠程度和機動車總阻抗對比Tab.4 Road network congestion and total vehicle impedance 本文采用的對整個網絡路段的機動車平均擁擠程度的評價指標公式表示為: 式中:fa表示路段a上的機動車流量;ca表示路段a上機動車的通行能力;A表示路網上機動車道的總數量。自行車平均擁擠程度評價指標同理。 由結果可知在路網上建設自行車專用道后可以有效減少系統的總阻抗并降低機動車道的平均擁擠程度。本文所提出的需求劃分模型,可以更為準確地預測模式需求,并在此基礎之上進一步降低系統總阻抗。 下面分析自行車專用道建設成本變化時,自行車專用道網絡的設計情況。在自行車專用道原建設成本的基礎上,分別以原成本的2 倍、3 倍、4倍、5 倍作為建設成本,規劃結果如圖12 所示。結果顯示,隨著建設成本的增加,禁行的機動車道的數量緩慢增加,而新建自行車專用道數量則逐漸減少直至不變。這說明當路段的建設成本較小時,傾向于選擇新建專用道,而當路段的建設成本較大時,則傾向于選擇禁行機動車的方案。表5展示了不同建設成本下的最優自行車路網規劃方案的影響。結果顯示,無論是機動車路網的平均擁擠程度,還是機動車和自行車的阻抗均有所增加,這說明自行車專用道的建設費用會對路網以及出行阻抗產生較大影響。 表5 不同建設成本下道路擁擠情況和出行阻抗Tab.5 Road congestion and travel impedance under different construction costs 圖12 不同建設成本下的不同建設規劃Fig.12 Construction plans under different construction costs 在其他參數相同的情況下,分別選取自行車阻抗系數φ為0.1、0.3、0.5、0.7、0.9進行自行車專用道網絡規劃,結果如圖13所示。 圖13 總阻抗隨阻抗系數的變化Fig.13 Variation in the total impedance with impedance coefficient 觀察發現,隨著系數的增高,自行車和機動車的總阻抗也隨之增加。這是因為在自行車阻抗系數和需求劃分的Logit 模型共同作用下,由于系數的增加,自行車的阻抗隨之增加,Logit模型中選擇自行車出行的概率會減小,而選擇機動車出行的概率會增大,導致機動車的阻抗也隨之增加。由此說明,自行車阻抗權重系數會影響需求劃分,進而影響最終的規劃結果,因而在實際規劃中,需要考慮自行車的阻抗影響。 在遺傳算法中,交叉和變異概率過高或者過低都會影響解的收斂。變異概率太小難以產生新的基因,而變異概率太大則會使算法成為隨機搜索。染色體的交叉可以產生新的個體,交叉概率較小時,產生新個體的速度較慢,從而收斂較慢;而當交叉概率較大時,會使高適應度的個體很快被破壞,從而導致收斂效果變差。在迭代次數都設為3 000 次,為了保證測試的準確性,同時改變交叉和變異概率的情況下,測試了不同的交叉和變異概率對收斂速度的影響。由圖14 可知,在不同的交叉和變異概率下,最小目標函數值存在差異。其中,在變異概率為0.1 而交叉概率為0.3 時,目標函數值最小(值為304 351.31)。因此在本研究中,交叉、變異概率分別取0.3、0.1較為合適。 圖14 目標函數值隨交叉和變異概率的變化Fig.14 Variation in objective function value with crossover and mutation probabilities 本文提出了一個基于雙層規劃模型的老城區自行車專用道網絡設計問題,上層決策專用道的規劃,下層分別用Logit 模型和UE 交通分配描述了出行方式選擇行為和路徑選擇行為,并提出嵌入了SRAM 和Frank-Wolfe 的GA 算法對模型準確求解。通過算例分析得到了以下結論:(1)本文所提模型和算法可以有效求解自行車專用道網絡設計。(2)與沒有需求劃分的模型對比可知,本文提出的模型可以有效地降低路網上的總阻抗,從而緩解交通擁堵。(3)自行車路段的建設成本、自行車出行阻抗系數均會影響最終的自行車網絡規劃方案。(4)交叉和變異概率會影響解的精度,分析表明本文交叉概率取值0.3,變異概率取值0.1較為合適。然而本研究中只考慮了自行車和機動車的出行方式,為了更加符合實際需求,后續可以從多種交通方式組合出行、下層問題基于SUE 交通分配求解等方面展開更多的研究。2.1 遺傳算法

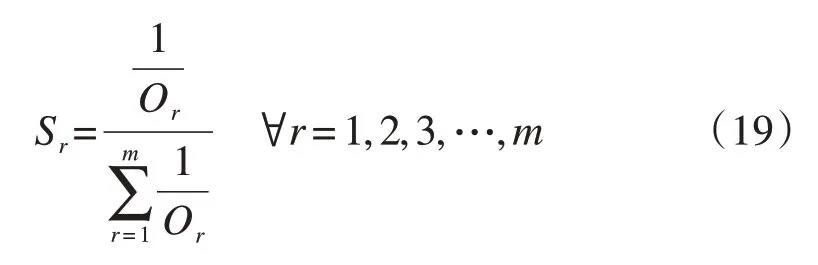
2.2 自適應平均算法

2.3 Frank-Wolfe算法


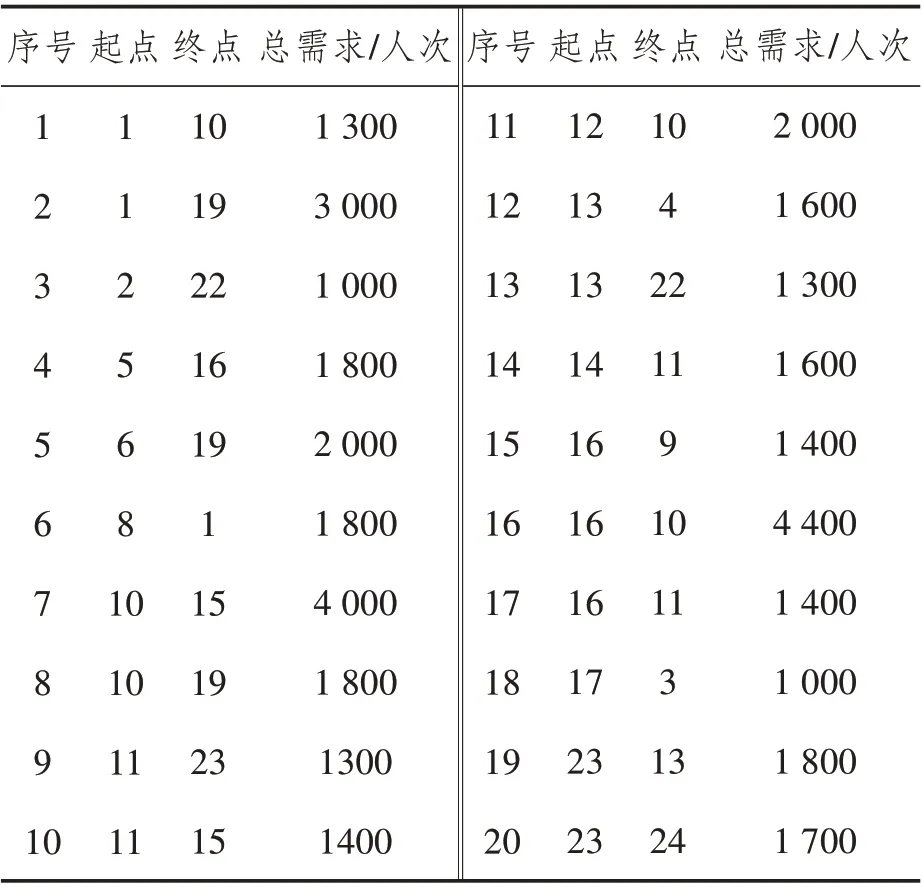
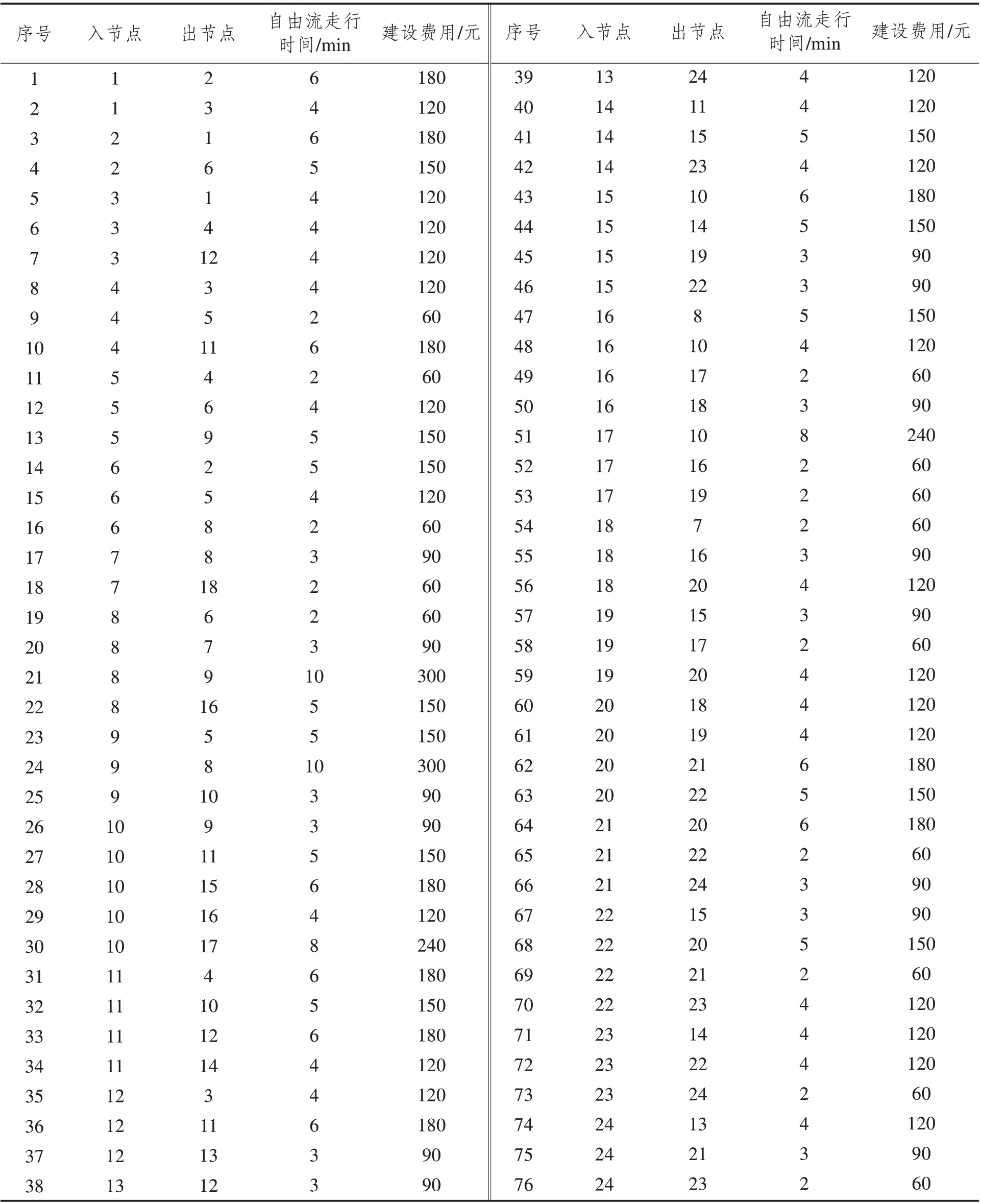
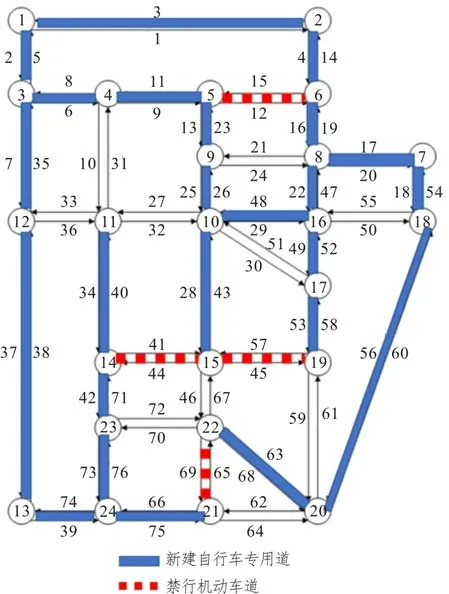
3 算例分析
3.1 模型結果
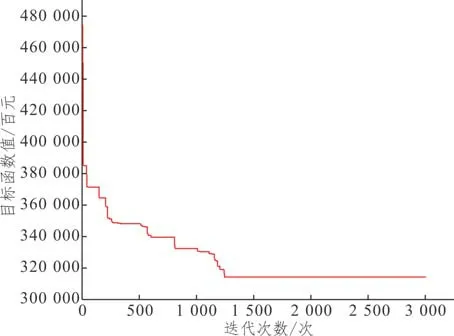
3.2 模型對比
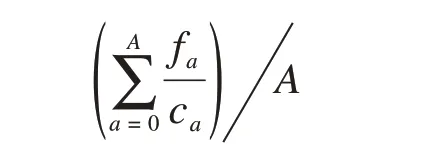
3.3 自行車專用道建設成本的影響分析
3.4 自行車阻抗系數的影響分析
3.5 交叉和變異概率對目標函數的影響
4 總結

