水平荷載作用下框架結構內力計算的樓層轉角法1

張年文

(廣東石油化工學院 建筑工程學院，廣東 茂名 525000)

反彎點法和D值法[1]是計算框架結構在水平荷載作用下內力的經典近似方法，在結構設計的初步設計階段應用較多。D值法要查表確定柱的反彎點高度，使用不便。孟煥陵等[2]介紹了計算框架結構水平位移的三種方法，推薦采用Smith-Coull方法[3]計算水平位移。Hsiao[4]提出了一種求解框架結構的水平位移和內力的懸臂梁力矩分配法，把多跨框架分解成多榀相同的單跨框架，分別計算各單跨框架的內力。Hu等[5]假定同一樓層的節點位移和轉角相等，利用計算機程序求解框架結構的水平位移，可以有效減少未知量的個數。R. Rahgozar等[6]提出了一個可以分析框架結構水平位移的數學模型。水平荷載作用下框架結構內力計算，據作者了解的信息，除了用計算機程序分析外無精度較高的近似求解方法。

力矩分配法是計算豎向荷載作用下連續梁、框架結構彎矩的經典漸近方法，該方法不能直接求解節點有水平位移的結構。本文提出了一種求解水平荷載作用下框架結構內力的近似方法，采用迭代計算每根柱(或者整個樓層柱)的節點轉角，迭代過程與懸臂梁的力矩分配法過程類似，求解出所有柱的節點轉角后，根據柱的節點轉角、樓層剪力計算樓層的相對水平位移，然后根據轉角位移方程計算梁、柱端初始彎矩(類似力矩分配法的固端彎矩)，采用力矩分配法求解梁、柱端彎矩。

1 基本方程

1.1 基本假定

水平荷載下框架結構水平位移、內力計算，采用如下假定：

(1) 框架結構的樓板為剛性樓板，只考慮樓板平動產生的水平位移；(2) 每個樓層梁、柱節點處的轉角相等；(3) 所有荷載作用在樓層節點上；(4) 不考慮柱的軸向變形；(5) 柱底為固定端。

1.2 框架梁、柱端彎矩

不考慮柱的軸向變形，連接節點(i,j)(表示第i層的第j個節點)和節點(i,j+1)的梁端彎矩可表示為Mi,j+1,j=4ki,j,j+1θi,j+2ki,j,j+1θi,j+1,Mi,j,j+1=2ki,j,j+1θi,j+4ki,j,j+1θi,j+1。式中：Mi,j,j+1為梁在節點j+1端的端彎矩，最末的下標表示所在節點端；ki,j,j+1為梁的線剛度,ki,j,j+1=ki,j+1,j；θi,j為節點(i,j)的轉角；柱端、梁端的彎矩、轉角以順時針方向為正，逆時針方向為負。

1.3 樓層剪力

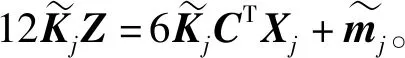
1.4 基本方程

2 轉角法計算框架水平位移、內力過程

2.1 節點轉角計算

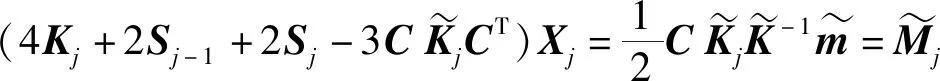
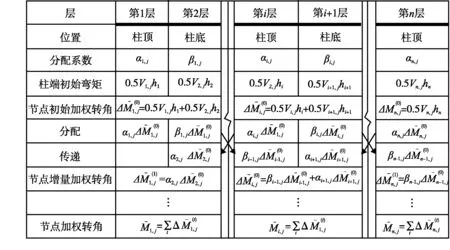
圖1 樓層加權轉角的計算

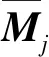
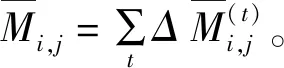
X的計算與Xj的相同，在此不再累述。

2.2 樓層水平位移計算

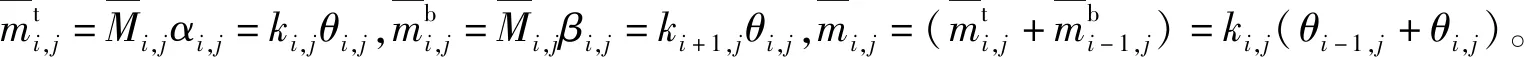
2.3 梁、柱端彎矩計算

算出節點轉角和樓層水平位移后，根據梁端彎矩表達式、柱端彎矩表達式可得梁、柱端初始彎矩，把初始彎矩看成是固端彎矩，采用經典的力矩分配法可得梁、柱端彎矩。

3 算例分析

圖2為3層框架結構的平面及立面示意圖，該算例是D值法分析框架結構內力的經典算例[8]。算例中的結構受橫向水平力作用時，全部5榀框架參與受力。圖2b中給出了樓層標高處的總水平力，柱邊、梁上的數值為每根梁、柱線剛度相對值，柱邊、梁下帶圈的數值表示單榀框架的梁、柱編號。采用樓層轉角方法，邊柱和中柱分別計算加權轉角，由加權轉角、樓層剪力可得樓層層間水平位移和樓層水平位移，計算結果和誤差見表1。由表1可看出，雖然樓層轉角法計算得出的節點轉角與有限元解誤差較大，但是樓層水平位移與有限元解誤差很小，最大誤差不到1%，遠優于D值法。

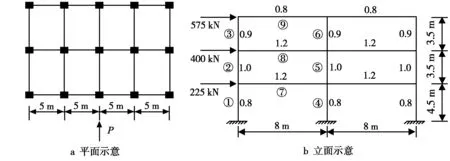
圖2 算例框架結構的平、立面示意

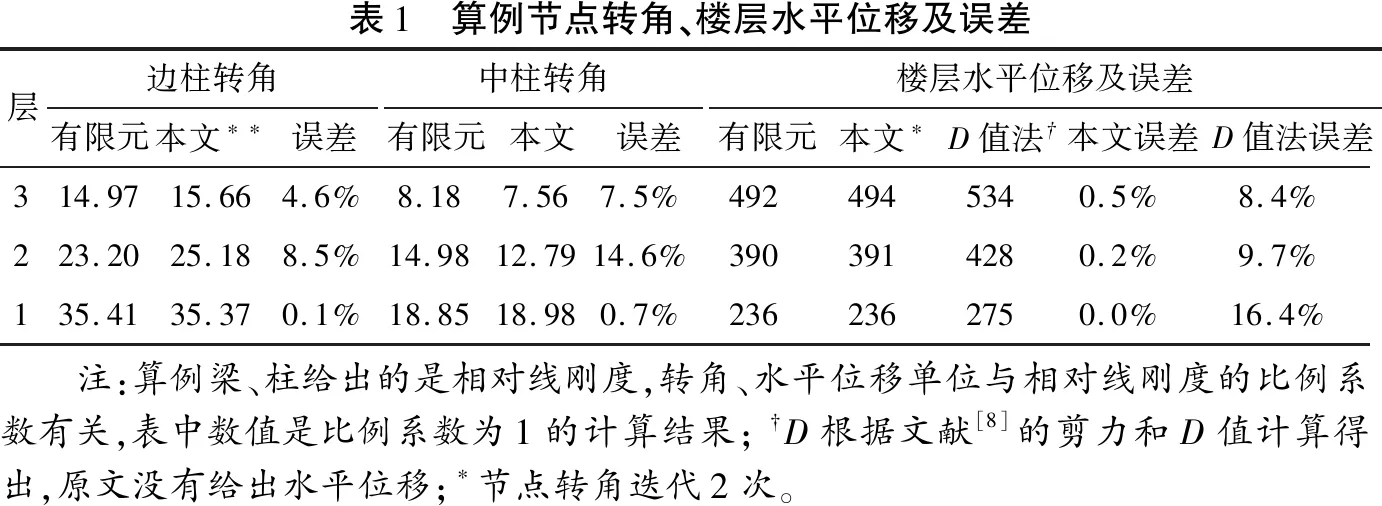
表1 算例節點轉角、樓層水平位移及誤差層邊柱轉角有限元本文??誤差中柱轉角有限元本文誤差樓層水平位移及誤差有限元本文?D值法?本文誤差D值法誤差314.9715.664.6%8.187.567.5%4924945340.5%8.4%223.2025.188.5%14.9812.7914.6%3903914280.2%9.7%135.4135.370.1%18.8518.980.7%2362362750.0%16.4% 注:算例梁、柱給出的是相對線剛度,轉角、水平位移單位與相對線剛度的比例系數有關,表中數值是比例系數為1的計算結果;?D根據文獻[8]的剪力和D值計算得出,原文沒有給出水平位移;?節點轉角迭代2次。

由節點轉角和樓層水平位移，可得梁、柱端初始彎矩，把初始彎矩看成梁、柱端固端彎矩，不平衡彎矩分配兩次的結果見表2。梁、柱端彎矩最大誤差出現在頂層中柱底端彎矩，為1.7%，除此外頂層中柱頂端彎矩和此節點梁端彎矩誤差為1.6%。D值法的解最大誤差出現在柱②底端彎矩，誤差為18.2%；誤差不小于10%的梁、柱端彎矩有7個，約占18個桿端彎矩的39%。可見本文方法計算框架結構梁、柱端彎矩具有明顯的優勢。

把同樓層的所有柱看成整體求解可得1～3層的節點轉角分別為27.41、18.96和11.49，樓層的水平位移分別為230、378和475，誤差分別為2.5%、3.3%和3.5%，比D值法計算的樓層水平位移精度高，不及單根柱計算的樓層水平位移精度，優勢是計算一次梁、柱節點轉角。

4 結論

提出了一種求解水平荷載作用下框架結構梁、柱端彎矩的近似方法，方法采用迭代計算節點的加權轉角(量綱與彎矩相同)，計算過程與彎矩分配法求解懸臂梁的桿端彎矩類似；算出所有柱的節點轉角后，計算樓層水平位移，根據轉角位移方程計算桿端彎矩(類似力矩分配法的固端彎矩)，然后利用彎矩分配法計算梁、柱端彎矩。本文方法，也可把所有柱看成一個整體，計算柱的節點轉角，算例表明計算結果比D值法的計算精度高，不及本文方法柱分開計算的精度高，優勢是只計算一次梁、柱節點轉角。算例的計算結果表明，樓層轉角法比常用的手算方法計算精度高，求解過程避免了查表，是一種計算精度高的近似方法。

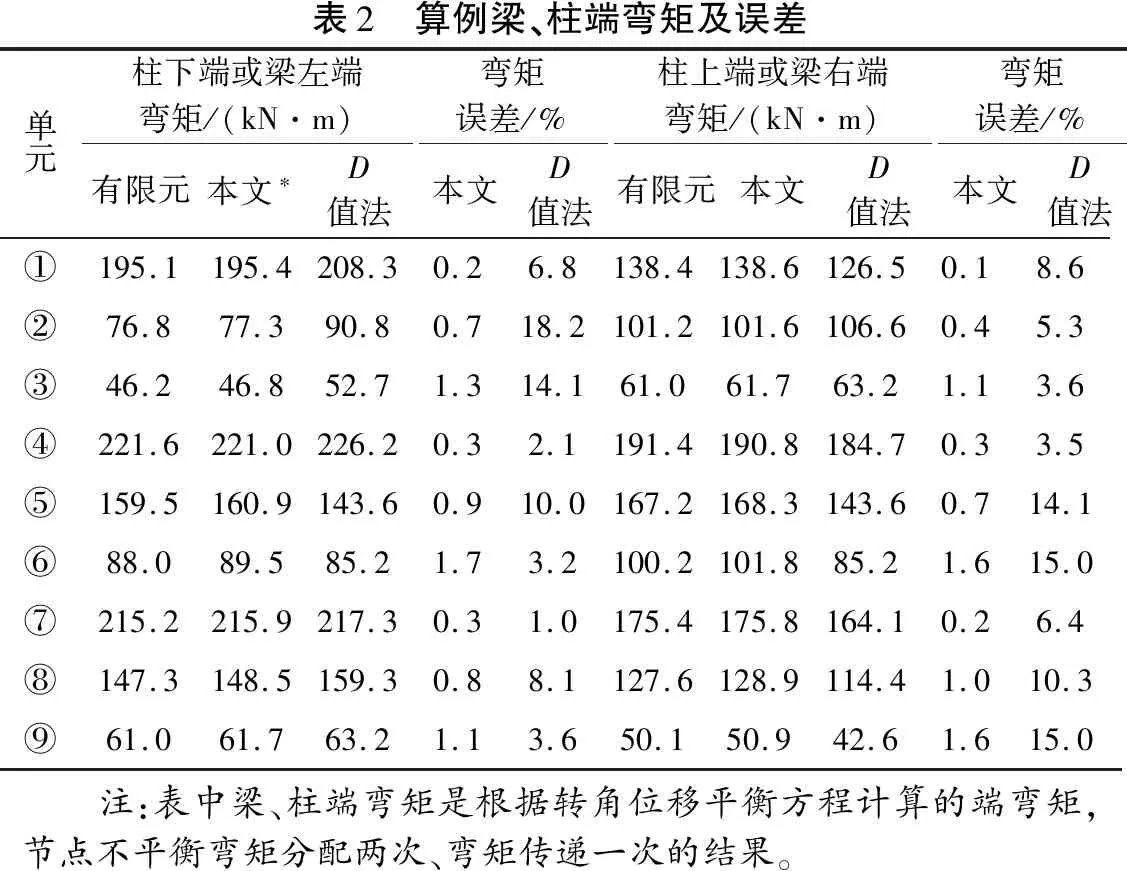
表2 算例梁、柱端彎矩及誤差單元柱下端或梁左端彎矩/(kN·m)有限元本文?D值法彎矩誤差/%本文D值法柱上端或梁右端彎矩/(kN·m)有限元本文D值法彎矩誤差/%本文D值法①195.1195.4208.30.26.8138.4138.6126.50.18.6②76.877.390.80.718.2101.2101.6106.60.45.3③46.246.852.71.314.161.061.763.21.13.6④221.6221.0226.20.32.1191.4190.8184.70.33.5⑤159.5160.9143.60.910.0167.2168.3143.60.714.1⑥88.089.585.21.73.2100.2101.885.21.615.0⑦215.2215.9217.30.31.0175.4175.8164.10.26.4⑧147.3148.5159.30.88.1127.6128.9114.41.010.3⑨61.061.763.21.13.650.150.942.61.615.0 注:表中梁、柱端彎矩是根據轉角位移平衡方程計算的端彎矩,節點不平衡彎矩分配兩次、彎矩傳遞一次的結果。