低畸變離軸三反光學系統設計

王欣，王春艷，孫昊，劉歡，趙義武

（長春理工大學 光電工程學院，長春 130022）

星模擬器對航空、航天技術的發展起著至關重要的作用，目前正朝著長焦距、大口徑、寬光譜、輕量化方向發展。由于星模擬器要模擬幾光年甚至更遠星體目標，因此對光學系統設計提出了更高的要求。為精確地校正航天器的姿態，要求星模擬器工作在寬光譜波段的同時可以模擬多星[1]。美國 McDonnell Douglas Aerospace研制的折射式星模擬器可模擬約50個星點，最大視場為 25°× 25°，單星張角精度優于 100″；中國科學院長春光學精密機械與物理研究應用光學國家重點實驗室研制的小型星模擬器，可模擬2～8等星，視場為10.5°×7.5°，單星張角優于40″；哈爾濱工業大學超精密光電儀器工程研究所研制的星模擬器采用改進的卡塞格林系統，可模擬 0～5 等星，視場為 28'，準直性優于±120″[2]。

離軸反射式光學系統由于無中心遮攔、工作波段寬、無色差等優點可應用于星模擬器設計中，但由于反射鏡優化變量少，離軸式光學系統像差不易控制。因此借助自由曲面良好的面型表征能力和平衡非對稱像差的優勢，使離軸反射式大視場、低畸變的光學系統設計成為可能。

1 光學系統設計理論

1.1 初始結構求解方法

離軸反射式系統通常求解方式是將共軸光學系統添加孔徑偏心量和視場傾斜角，來獲得理想的離軸反射式系統初始結構。對于同軸系統，三階像差表達式為：

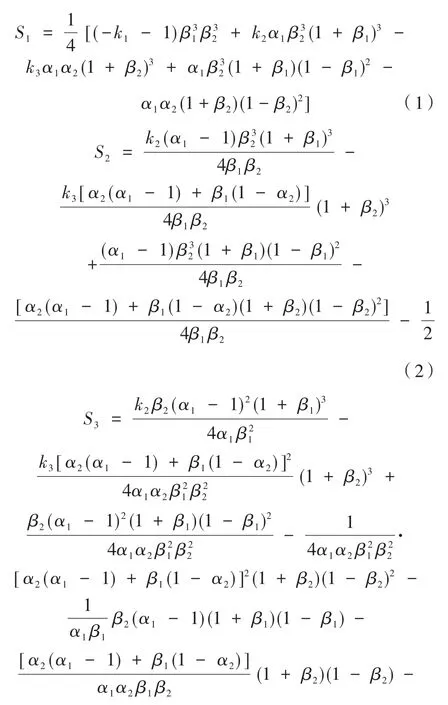
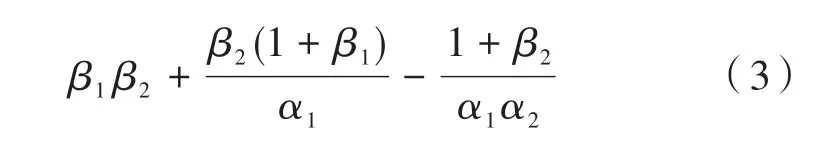
式中，S1、S2、S3分別為球差、彗差、像散；-ki表示第i面反射鏡的二次錐面系數；α1、α2分別為次鏡對主鏡遮攔比和三鏡對次鏡遮攔比；β1、β2為次鏡及三鏡的垂軸放大率[3]。

選擇無過渡像面的成像形式時，要求次鏡對主鏡的遮攔比α1＞0，三鏡對次鏡的遮攔比α2＞0，次鏡的垂軸放大率β1＜0，三鏡的垂軸放大率β2＜0，系統焦距f'＞0，同時反射式系統要求場曲S4=0[4]。在滿足無過渡像面的情況下，求解α1、α2、β1、β2使得S1、S2、S3數值較小，且間隔合理。通過分析計算最終選擇的初始結構數據為：α1=0.6，α2=0.4，β1=-1.4，β2=-0.5，此處取k1=-1，令S1=0，S2=0，計算可得k2=0.4，k3=-5，其三階像差分別為：S1=0，S2=0，S3=0，同軸初始結構如圖1（a）所示，求解的初始結構具有很好的成像質量，利于后期離軸系統的進一步優化設計。對得到的同軸初始結構添加邊緣視場并進行離軸化處理，由于系統要求箱體寬小于780 mm，故光學系統的設計應盡量緊湊，設主鏡的孔徑偏心量為-300 mm，離軸角-3°，可滿足系統要求，得到的離軸初始結構如圖1（b）所示。

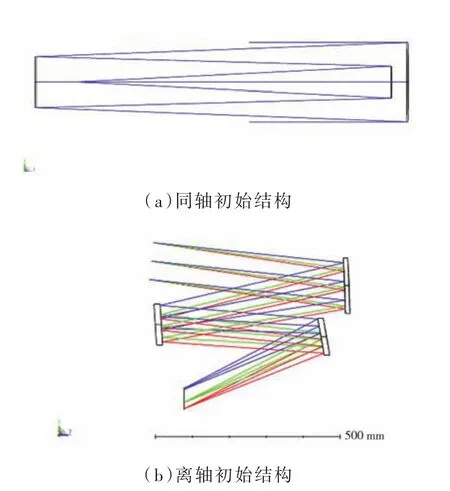
圖1 初始結構

1.2 矢量像差理論

對于非旋轉對稱系統，同軸像差理論不再適用，因此引入了矢量像差理論用于對離軸光學系統的分析設計。矢量波像差是由各個表面因視場離軸所引起的像差貢獻之和，當每個表面的偏心量及離軸量確定之后，系統的波像差也隨之確定[5]。

則由主鏡傾斜及偏心所引起的波像差為：

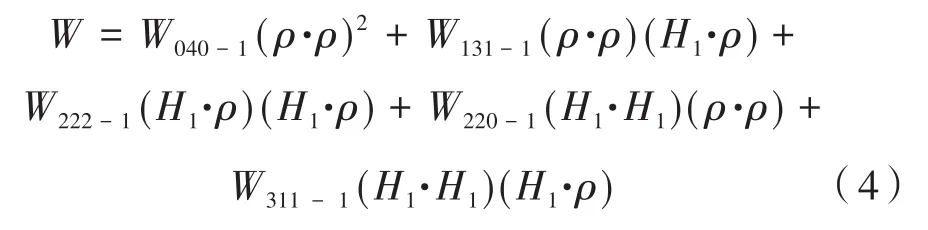
式中，第一項至第五項分別表示球差、彗差、像散、場曲及畸變；H表示歸一化的視場矢量；ρ表示歸一化的光瞳矢量[6]。

由于所設計的離軸初始結構引入了軸外視場，因此對式（4）分別分析軸上及軸外視場所引起的波像差變化，即W=W040-1(ρ·ρ)2+W0+W1，其中：

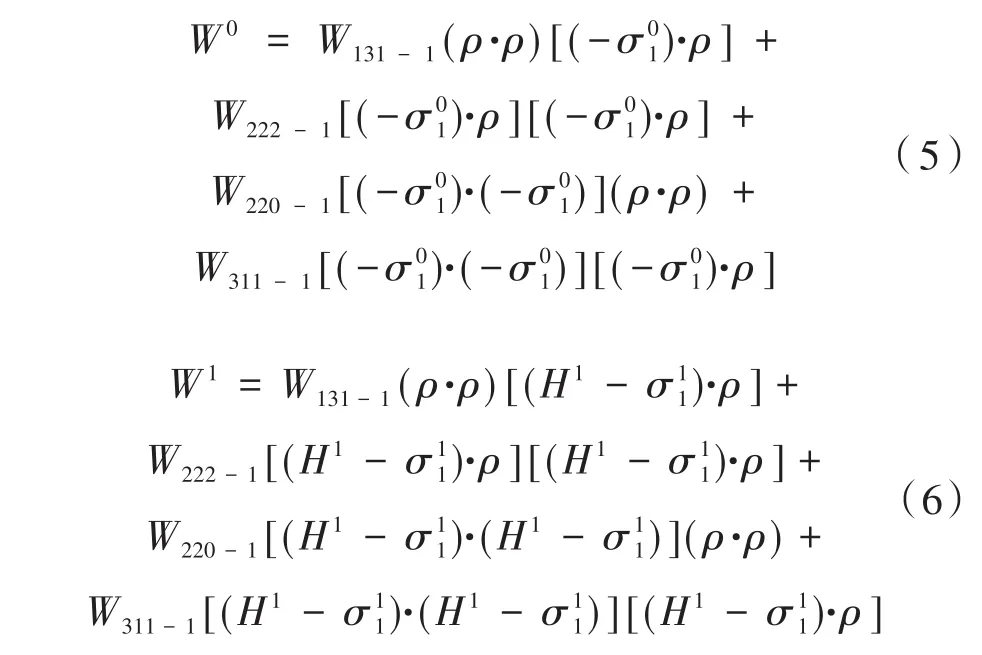
式中，W0和W1分別代表軸上視場分量及軸外視場分量在系統波像差中所做的貢獻。分析式（6）可知，球差不受視場離軸影響，其余均受離軸影響較大，經ZEMAX仿真模擬，其數值分別為：S1=0，S2=-0.002 15，S3=0.000 34，S4=-0.007 48。

2 設計實例與像質分析

2.1 系統性能及指標

畸變對光學系統的成像清晰度沒有影響，但它會直接影響星點的位置精度，因此消除系統畸變是設計的重點。根據畸變定義有：

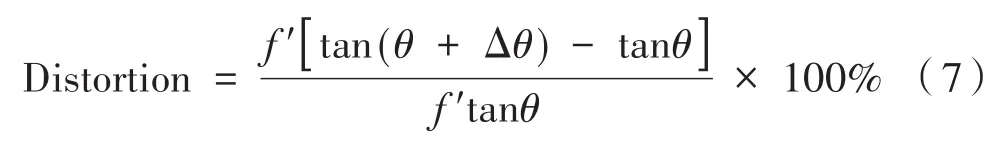
為保證系統的成像位置精度，要求畸變值小于0.005 6%，模擬星等的范圍為0～6星等，計算可得光源的對比度為 250∶1[7-8]，故本課題考慮選擇像素大小為0.026 mm，型號為LCX023CMT的液晶光閥作為光源，其畫幅尺寸為27.3 mm×21.3 mm，系統指標如表1所示。

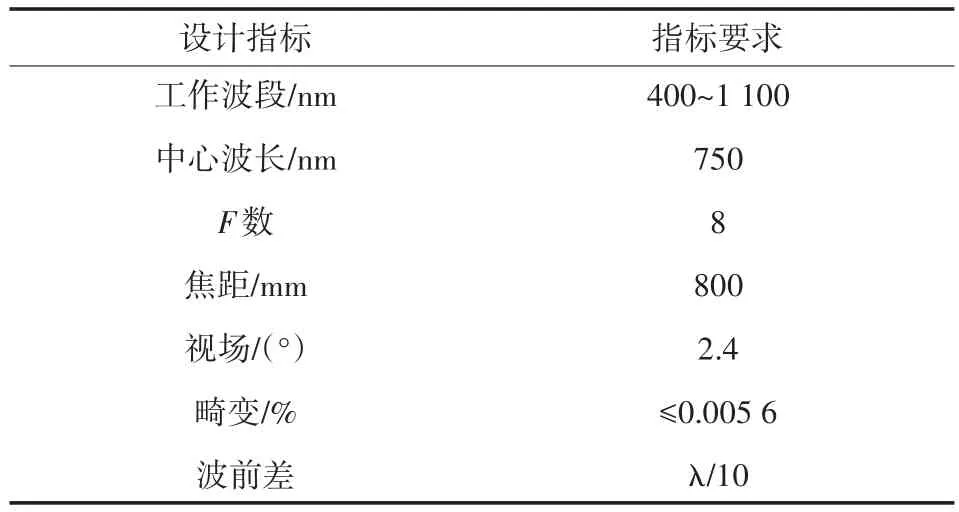
表1 光學系統設計指標

2.2 設計結果

由于傳統面型對于該指標實現較為困難，因此在所獲得的初始結構中添加自由曲面，由于Zernike多項式在單位圓上的正交性，在對其各項單獨進行優化時互不影響，故次鏡選用Zernike多項式來平衡系統的像差；三鏡采用XY多項式描述的自由曲面，選取六階以下的項數進行優化，各項數均有選擇，以此來保證彌散斑的對稱性及圓整型[9]。

最終設計的結構形式如圖2所示，主鏡y方向傾斜角度為-5.1°，同時y方向的偏心距離為-190 mm，三鏡y方向傾斜角度為3.8°，總長為649 mm，整體高度為335 mm，寬度為164 mm，最終設計的光學系統有很好的成像質量，光能損失小，邊緣視場畸變小，設計上的孔徑光闌位于主鏡左側500 mm處，孔徑光闌由于要與星敏感器入瞳嚴格銜接，以免造成光能的損失，因此將孔徑光闌置于主鏡左側較遠位置，后根據該距離定制箱體，箱體尺寸為900 mm×600 mm×500 mm，系統結構參數如表2所示。

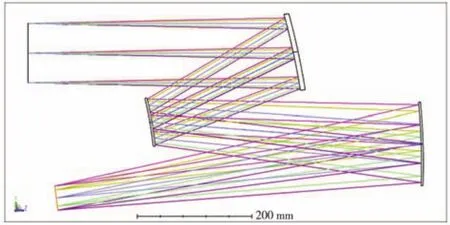
圖2 系統結構圖

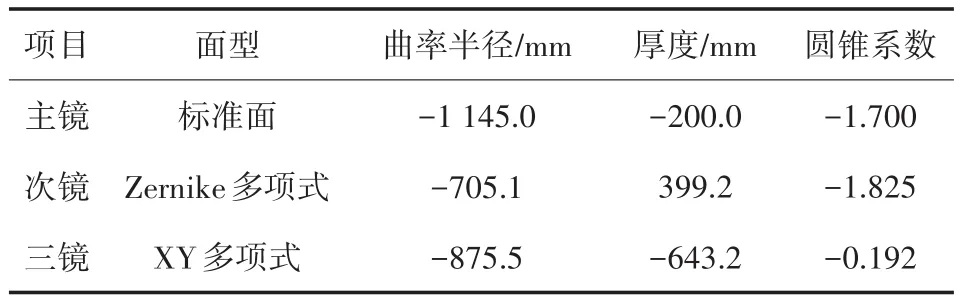
表2 系統結構參數表

在所設計的光學系統中，次鏡采用Zernike多項式所描述的自由曲面，參數如表3所示，三鏡采用XY多項式所描述的自由曲面，參數如表4所示，面型圖如圖3、圖4所示，次鏡口徑為Φ79 mm，表面矢高差為14.5 mm，三鏡口徑為Φ137 mm，表面矢高差為5.38 mm，可在MTC410單點金剛石車床上實現加工，采用基于單點金剛石車削技術的三軸聯動加工方法，采用該方法已實現Φ682 mm口徑、220 mm矢高的凹面反射鏡的加工。

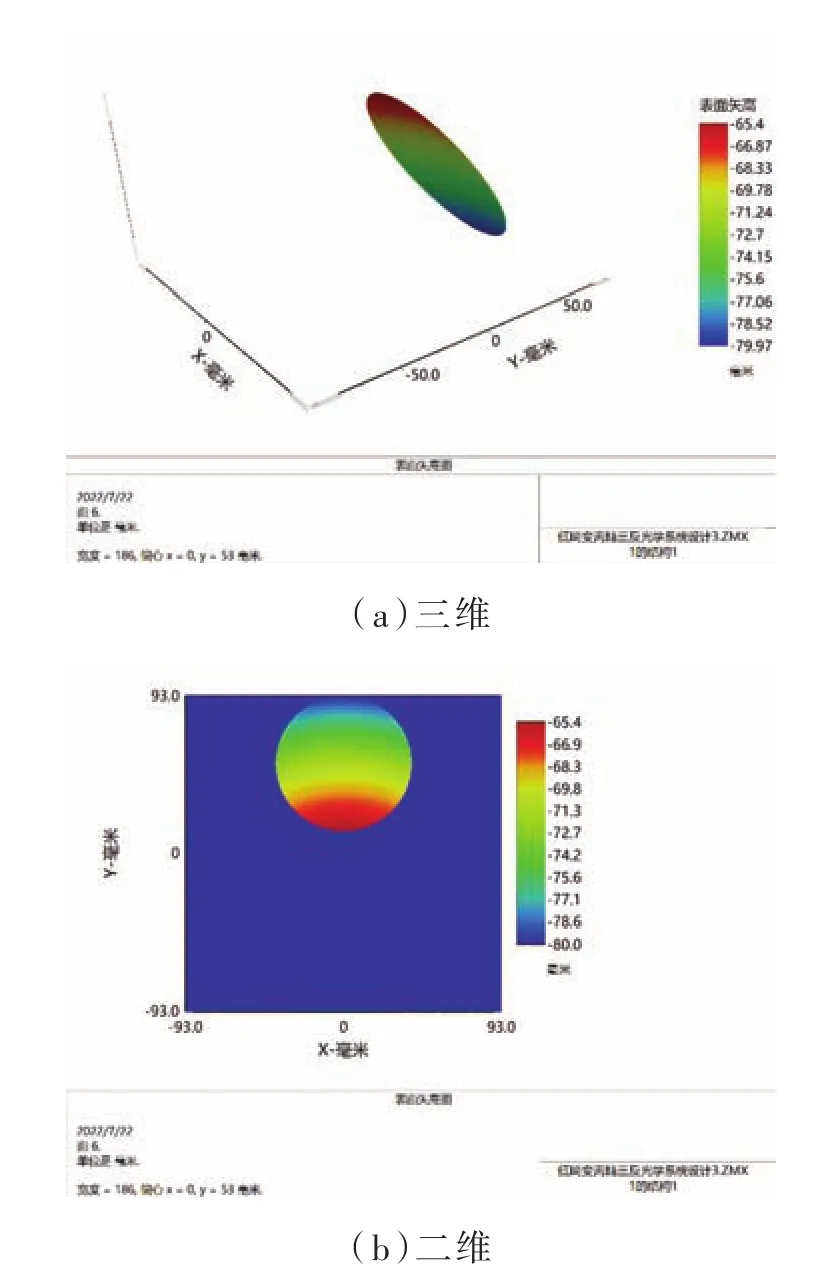
圖3 次鏡Zernike自由曲面的面型

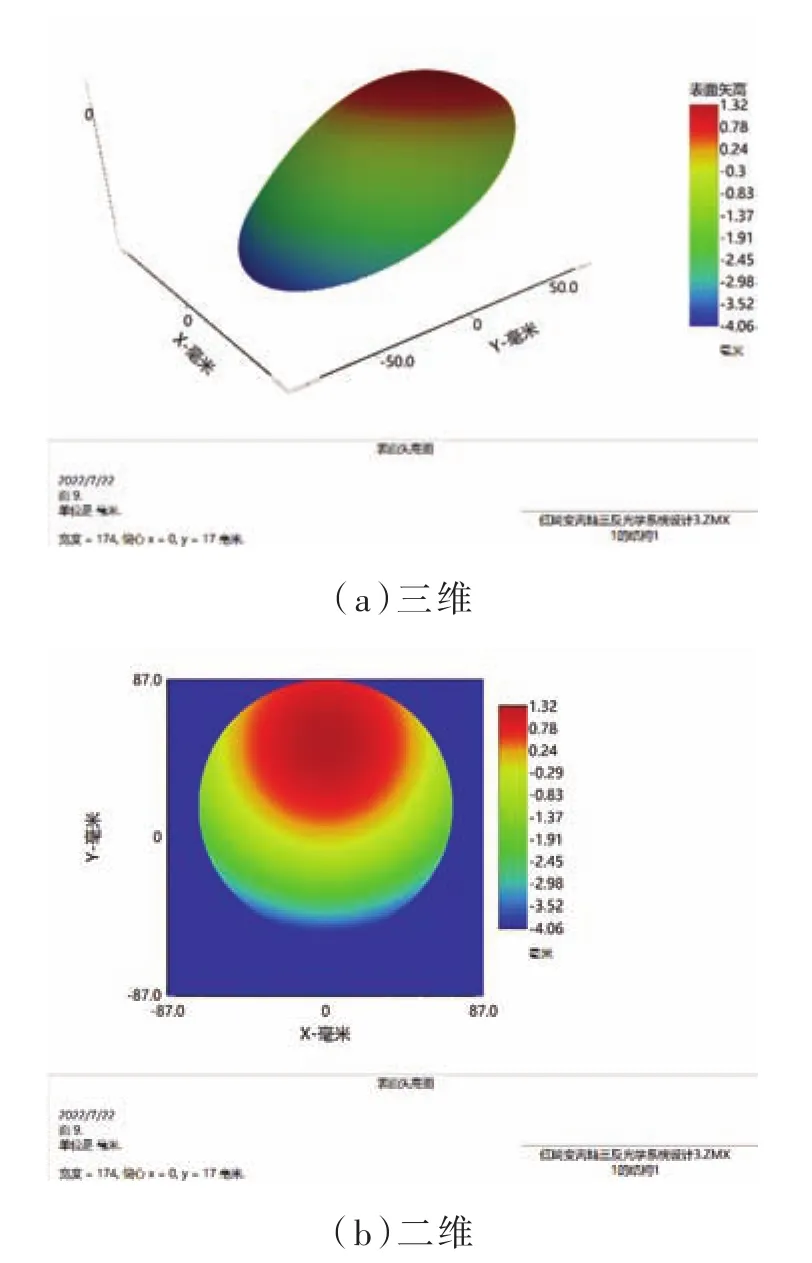
圖4 三鏡XY自由曲面的面型

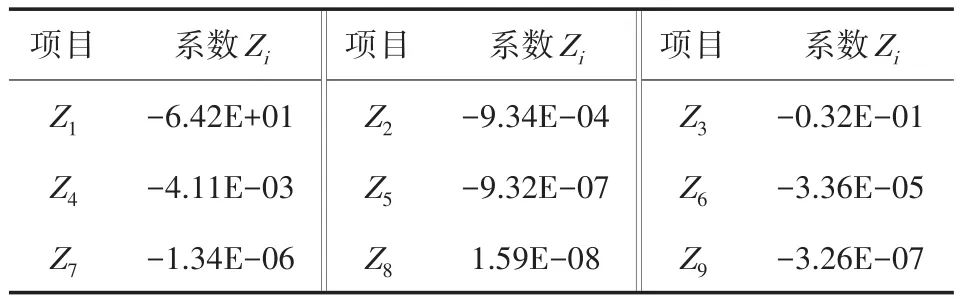
表3 次鏡Zernike多項式參數

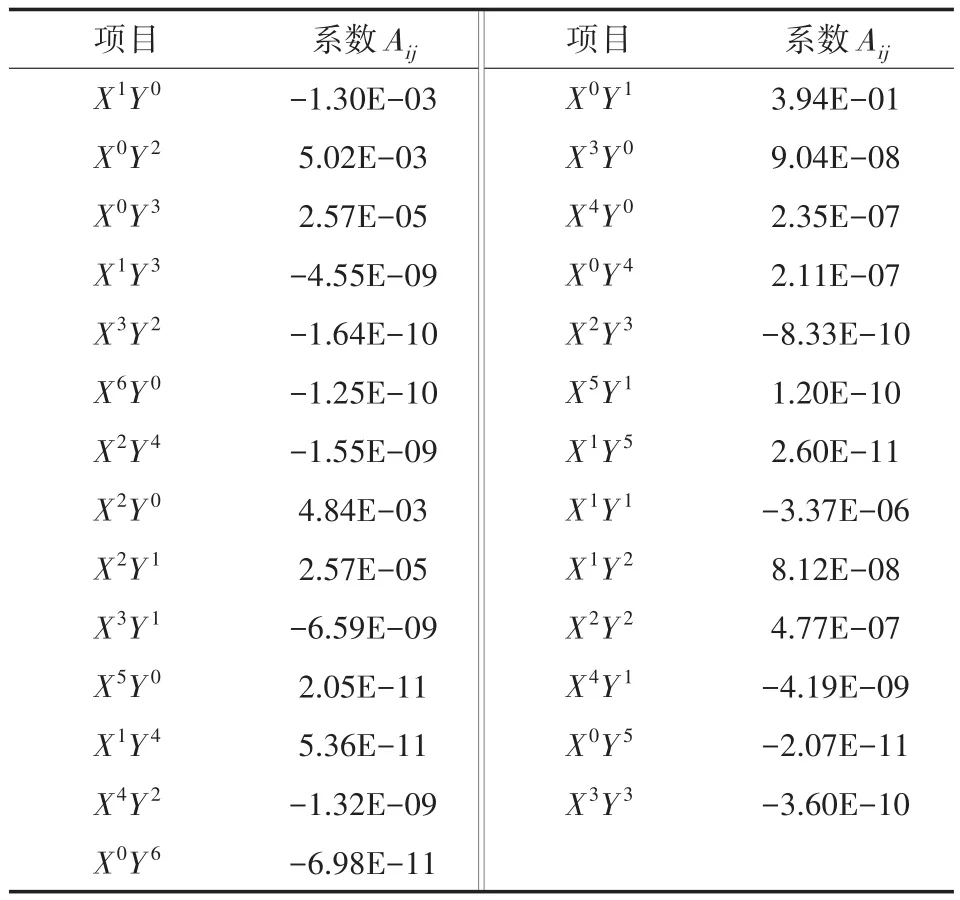
表4 三鏡XY多項式參數

主鏡、次鏡及三鏡口徑均屬于小口徑反射鏡，根據反射鏡的結構特點，選用背部中心支撐方式，可滿足裝調需求。

2.3 系統成像質量分析

光學傳遞函數是對光學系統成像質量的最綜合評價，它能直接地反應光學系統的性能[10]。選用像素大小為0.026 mm的液晶光閥作為光源置于像面處，故求得奈奎斯特頻率為：

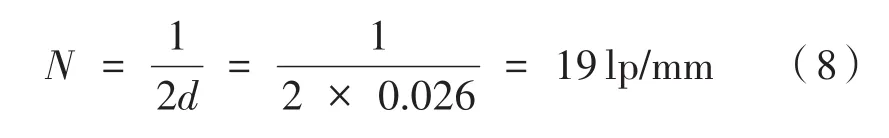
由于離軸反射式系統失去了旋轉對稱性，故分別在+y、-y、+x、-x采樣，分析圖5（a）～圖5（d）可知：最大畸變值為0.001 1%，優于0.005 6%；MTF曲線在19 lp/mm處均優于0.75，且接近衍射極限；質心點列圖表明能量中心與主光線偏差不大，設計的光學系統最大彌散斑半徑為0.458μm，彌散斑半徑均小于艾里斑且光斑較為圓整；最大波前差為0.005 2λ，優于λ 10，此結果表明該光學系統具有良好的成像質量。

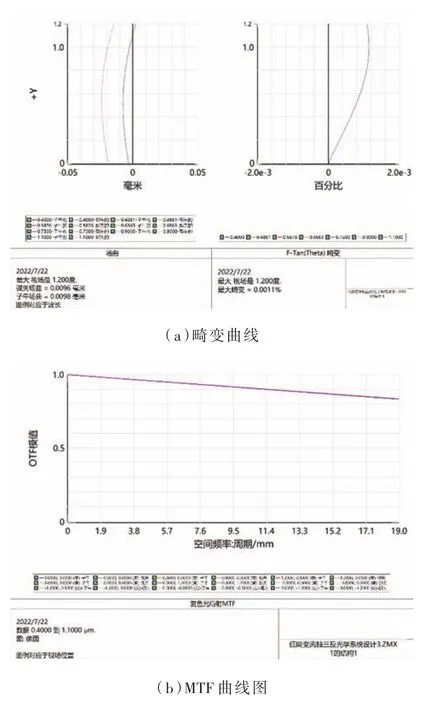
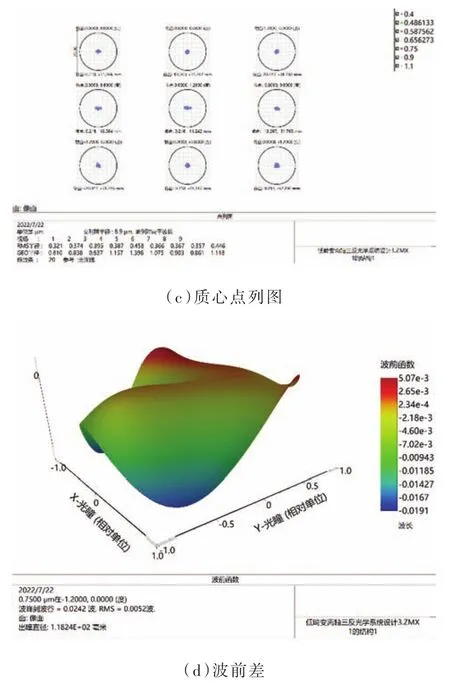
圖5 光學系統像質評價圖

3 結論

為克服反射式光學系統因增大視場所帶來的像質缺陷，本文基于矢量像差理論分析了視場及視場離軸所引起的像質變化，構建了基于自由曲面的像差校正模型。根據矢量像差理論所分析的結果，利用自由曲面的面型特征，有針對性地選取Zernike多項式的項數及XY多項式的階數，設計了含有自由曲面的大視場低畸變離軸三反光學系統。設計結果表明，在離軸反射式系統中引入不同形式的自由曲面，在一定程度上改善了各個視場的像質，并通過優化達到了預期的畸變要求。所設計的光學系統在2.4°的視場范圍內，所達成的像質較好，可用于高精度的星敏感器的標定。本次設計僅限于對復雜面型的應用研究，后續將從復雜面型的檢測技術研究展開。