主動降噪泄露變步長FxLMS算法研究

百文萌，王勁松，2，高慧杰

（1.長春理工大學 光電工程學院，長春 130022；2.長春理工大學 中山研究院，中山 528437）

主動噪聲控制（ANC）是一種利用聲波相消干涉原理，人為地產生與噪聲同頻、等幅、反相的“抗噪聲”達到降噪的新技術[1]。在整個ANC系統中，自適應控制算法可以稱之為其核心部分[2-3]，其中以計算量小和容易實現為優點的濾波-x最小均方（FxLMS）算法在主動降噪中廣泛應用[4]。在FxLMS中，一個不可忽視的存在即為步長因子，因為它既是決定算法能否收斂的關鍵因素，也是判斷收斂速率和穩態誤差大小的重要因素。所以，對于FxLMS算法的改進始終是個熱門課題。改進的主要目的是在算法收斂的情況下，提高算法迭代過程的收斂速率、降低穩態誤差以及有利于算法的硬件實現。目前比較經典的改進算法有歸一化LMS算法、泄露FxLMS算法等。其中，雖然歸一化LMS算法的收斂速率確有改善，但是在算法穩定后，步長因子不能達到一個較小的值，致使穩態誤差較大；泄露FxLMS算法是加入泄露因子可以約束次級信號，降低FxLMS算法不穩定的機會，但是收斂速度沒有得到明顯的改善。

針對上述步長調整原則和變步長算法的優缺點，提出一種泄露變步長的FxLMS算法來克服傳統固定步長的缺點，提高算法的穩定性。本文將對FxLMS算法和改進后的算法分別進行仿真分析，并最終將其運用在雙通道主動噪聲控制的結構中，以提高降噪效果。

1 噪聲主動控制算法的基本原理

FxLMS算法是在最小均方（LMS）算法的基礎上考慮到了次級路徑存在的影響，由Morgan、Widrow和Burgess獨立推導得到[5-6]。前饋單通道FxLMS算法如圖1所示，x(n)為輸入的初始信號，d(n)為初始信號通過初級傳遞函數P(z)到達誤差傳感器附近的期望信號，e(n)為誤差傳感器接收到的誤差信號，W(z)代表自適應濾波器。r(n)是x(n)經過次級路徑傳遞函數估計S?(z)后的濾波信號，將r(n)和e(n)共同作為控制器W(z)的另一個輸入信號，通過算法處理后獲得的控制器輸出信號y(n)再通過次級路徑傳遞函數S(z)可在誤差傳感器附近得到一個與期望信號相抵消的控制信號yp(n)，從而達到降噪的目的。

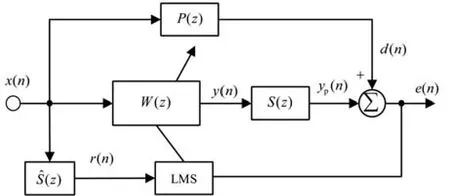
圖1 基于FxLMS算法的ANC系統框圖

設濾波器的長度為L，其算法具體如下：

（1）某一時間初始信號的輸入為：

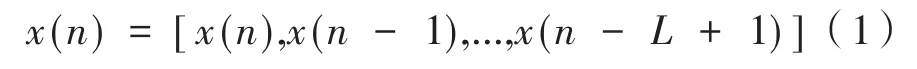
（2）x(n)經過W(z)后的信號y(n)為：

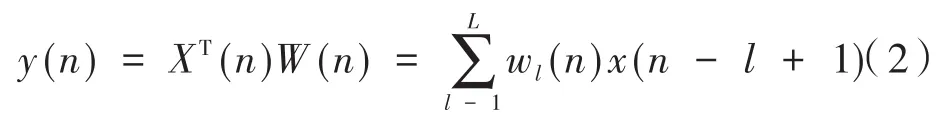
（3）y(n)經過次級路徑后輸出的控制信號yp(n)為：

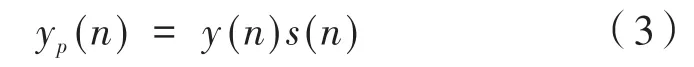
（4）x(n)經過后輸出的濾波信號為：

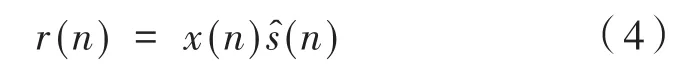
（5）誤差傳感器處的誤差信號為：

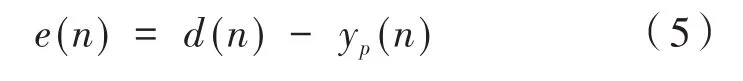
（6）通過迭代求取新的濾波器抽頭系數：

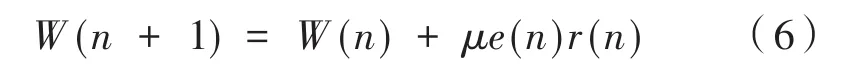
式中，步長μ為一個固定值，取值需滿足：

式中，λmax是初始信號向量自相關矩陣的最大特征值。

由上述的公式可知算法的收斂系數μ是一個固定的值，其取值的大小影響著算法收斂速度和系統的穩定性。經過仿真分析可得，步長取值較大時，可使算法較快收斂，但同時會使系統的穩態誤差增大，嚴重時會導致算法發散，步長取值較小時，可使算法的穩態誤差較小，使系統的穩定性更好，但是算法達到穩定時所需的時間較長。

2 改進的FxLMS算法

分析可知，步長是一個至關重要的存在，為了更好地兼顧收斂速度和穩態誤差這兩個關鍵因素，人們提出了變步長的改進思路[7]，即：在算法初期，為了保證有較高的收斂速率，應使步長因子的值處于一個較大的值，在算法末期，為了保證有較低的穩態誤差，則此時對應的步長因子的值也應該較小。在上述的步長設計思路下，考慮到權系數更新過程中由實際次級路徑下的數模轉換過程產生的量化誤差給系統帶來的泄露影響[8]，進而提出一種泄露變步長FxLMS算法。

2.1 歸一化FxLMS算法

由前文可知，FxLMS算法的權矢量迭代公式為：

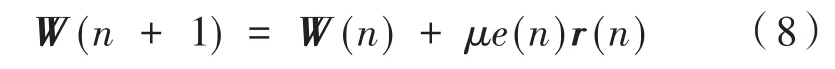
根據歸一化FxLMS算法可得步長因子公式為：

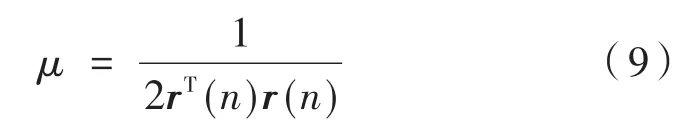
則權系數更新公式改寫成：

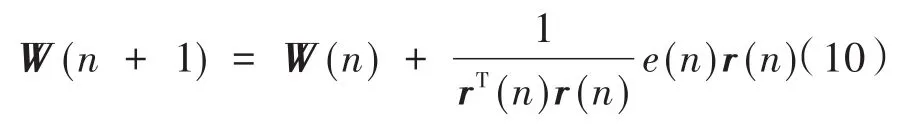
則更為可靠的實現方式[9]為：

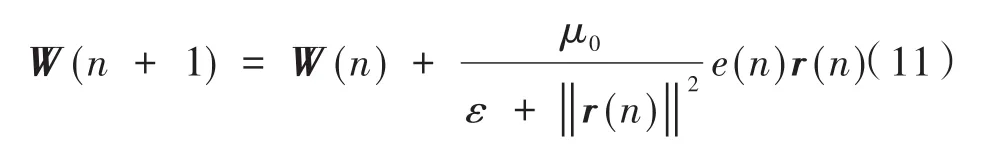
式中，μ0和ε均為正常數。當歐式范數平方‖r(n)‖2出現較小值時，易引起步長過大，從而導致算法發散，常數ε的存在則避免了此類情況的出現。對于存在的常數μ0，可以看作為步長參數，用來控制調節算法的收斂速率和失調量，當μ0=1和ε=0時，此時的遞推方程式（11）即為式（10）。

2.2 改進的FxLMS算法

由式（11）可得步長因子與輸入的初始信號的自相關矩陣有關。對算法的分析可知，此歸一化FxLMS算法的步長因子雖在自適應過程初始階段有變化，但在自適應過程趨于穩定之后其步長不能達到一個小的值，則穩態誤差會增大。在此基礎上改變步長，可用步長因子除以誤差向量的歐式平方范數，使步長在自適應過程初始階段有一個較大的值，且伴隨著迭代過程的進行，步長也將逐步降低，并最終穩定在一個較小的值，即降低穩態誤差，使系統更加穩定。有：

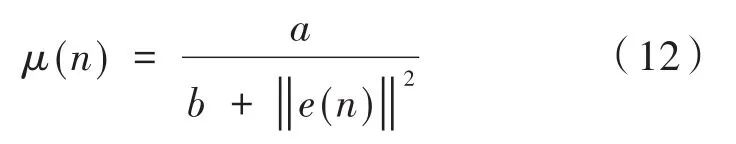
式中，誤差向量e(n)的歐式平方范數可以寫為，隨著采樣次數的增加可知，步長μ(n)既和當前的誤差量e(n)有關，又和誤差向量迭代過程的前n步有關，因此，迭代步長是平滑下降的一個函數[10]，確保了步長在自適應過程的初期值較大，末期值較小，可以有效地降低穩態誤差。另外，固定參數a的選取影響著μ(n)的變化，受初始信號的影響，參數值不容易確定。由于此算法中μ(n)的值只能是不斷地下降，所以在應對非平穩隨機過程系統中的跟蹤能力較弱[11]。為此，可引入對數函數對其進行改進，使得μ(n)的值在一定的范圍內不斷地進行調整，有：

其中，γ的數值影響步長函數μ(n)的陡峭化程度，γ的值越大，其整體的變化率就越快，α和β的值確定了μ(n)的變化范圍。這里的e(n)2代表第n次迭代中瞬時誤差量的平方值，對比上式e(n)的歐式平方范數而言，運算量大幅度降低，只需要一個標量的平方運算，更易于硬件的實現，并且由于μ(n)僅與當前誤差向量e(n)有關，不是單純地不斷下降，而是根據當前的誤差在范圍內不斷地調整，提高了算法的實時性，使算法也適合于非平穩過程。

此時的權系數更新公式為：

本文提出的泄露變步長FxLMS是在式（14）的基礎上，考慮了實際數模轉換過程中量化誤差帶來的泄露影響，可將上式的權值更新公式改寫為：

式中，η是泄露系數，是小于且接近1的一個常數。

2.3 次級通道辨識

由前面的分析可知，在更新濾波器抽頭系數的迭代公式中含有濾波-x信號矢量r(n)，r(n)是x(n)通過傳遞函數估計模型求得。對次級路徑建模，如圖2所示，選擇LMS算法模塊，獲得傳遞函數估計模型的值。

圖2 次級通道建模原理圖

次級路徑建模的步驟如下：

（2）使用誤差傳感器接收由揚聲器產生的對消信號y(n)：

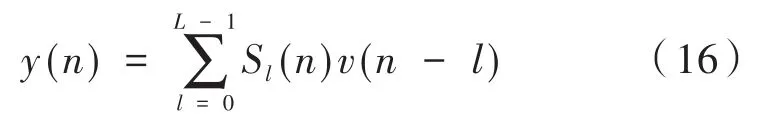
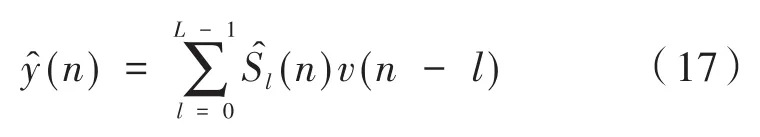
（4）計算路徑的實際模型和估計模型之間的輸出差值：

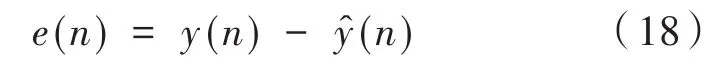
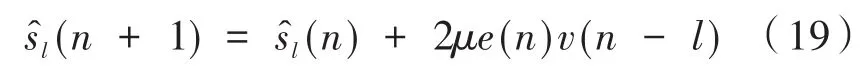
（6）重復以上迭代過程，利用誤差信號e(n)不斷調節權系數，直至達到設定要求為止，同時將得到的的系數值存儲起來，方便后續Fx-LMS算法使用。

現根據圖2所示的過程進行次級路徑建模仿真，為了驗證結果的有效性，設傳遞函數[12]為：

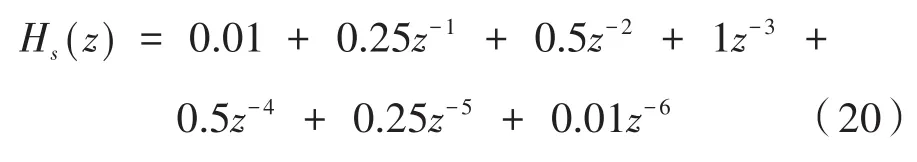
通過對其進行建模分析，取μ=0.01作為建模過程中LMS算法的步長因子的值，仿真的結果如圖3所示，從圖3（a）中可看出，識別誤差從采樣點數100往后接近于零，系統也趨于收斂。即建模仿真實驗對次級路徑的識別效果是穩定的。另外，通過仿真建模實驗得到的實際路徑和估計路徑的濾波器權值也非常接近，仿真結果表明實驗有良好的估計值，辨識結果準確。

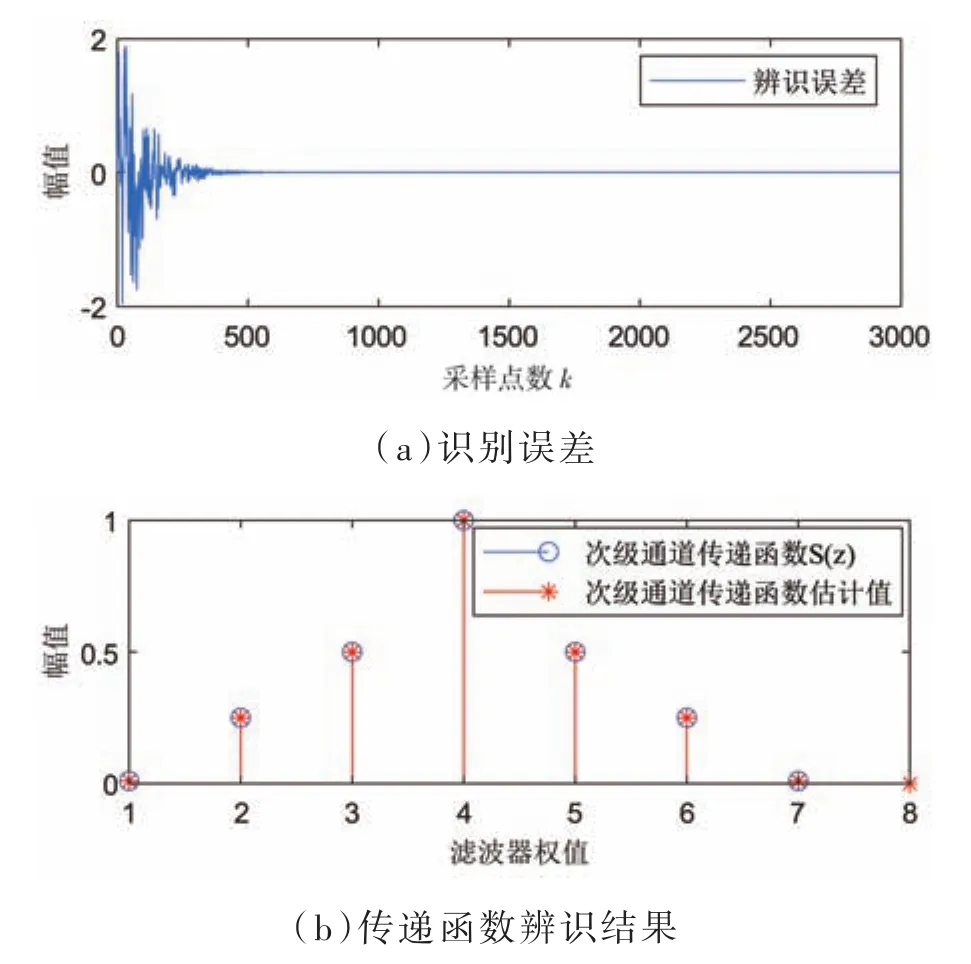
圖3 次級通道傳遞函數建模仿真實驗

2.4 改進FxLMS算法的仿真分析

仿真中，將傳統的FxLMS算法和本文的改進FxLMS算法進行比較，由于單一的頻率信號在實際應用中很少存在，而更常見的是帶有一定帶寬的噪聲信號，因此本文的仿真實驗中采用的是混合信號，將x(t)=s(t)+v(t)作為輸入信號，其中v(t)是信噪比SNR=7的隨機白噪聲，s(t)是一個混頻信號，則：

即該信號由頻率分別為200 Hz、350 Hz和600 Hz組合構成。考慮到收斂速度和實現的硬件成本，選取濾波器的階數為16，傳統FxLMS算法的固定步長取μ=0.012，改進算法仿真中取泄露因子η=0.999，步長函數各參數取β=0.012，α=0.003，γ值的大小決定其變化率，這里取γ=10。

仿真結果如圖4所示，圖4（a）和圖4（b）分別代表了FxLMS算法和泄露變步長FxLMS算法濾波的噪聲殘留。從圖中可知，噪聲經過這兩種算法的處理都得到了顯著的改善，然而對比觀察即可發現，在改進算法的處理下，噪聲殘留明顯有所降低，這是由于改進算法的步長是根據當前誤差向量在一定的范圍內不斷地進行調整，如圖4（c）所示，步長在迭代的過程中整體呈現下降的趨勢，并且在迭代的后期也處于較小值的狀態，因此，收斂后的穩態誤差較小，噪聲殘留也更低。

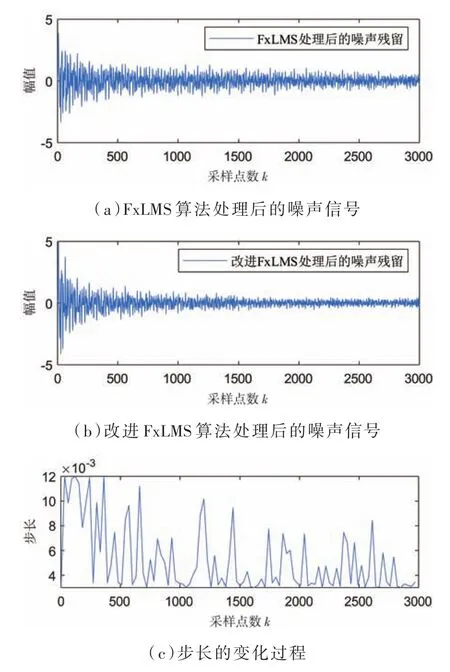
圖4 單通道兩種算法的仿真結果

為了驗證改進算法的優良性，把白噪聲作為輸入信號，對比FxLMS算法和改進的FxLMS算法的收斂性能，算法的各參數設定值不變，其均方誤差（MSE）如圖5所示，可以看出改進的FxLMS算法明顯比傳統的FxLMS算法的收斂速度快，且穩態誤差值也較低，整體的穩定性也更好。

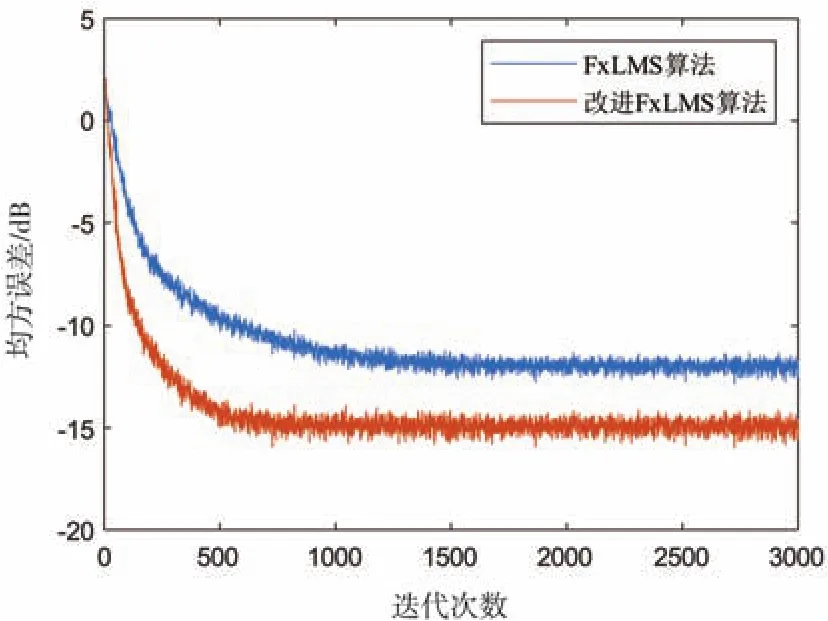
圖5 不同算法的MSE對比圖

圖6為單通道系統下不同算法處理后的功率譜。圖6（a）為經過傳統FxLMS算法降噪處理后的功率譜，其在中心頻率200 Hz、350 Hz、600 Hz處的幅值下降為13.8 dB。圖6（b）為提出的泄露變步長FxLMS算法經過降噪處理后的功率譜，其在中心頻率處的幅值下降為19.6 dB。

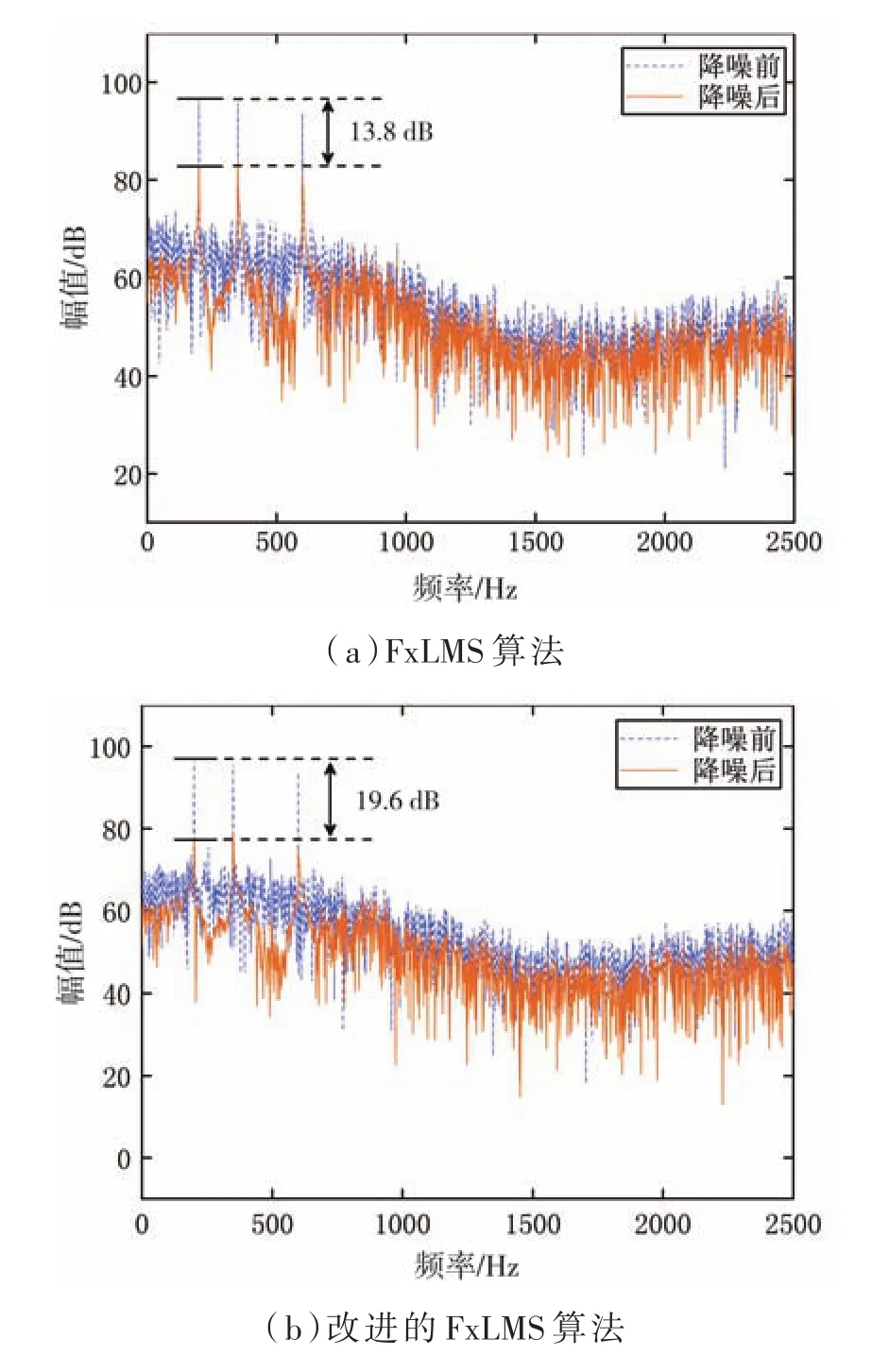
圖6 不同算法降噪前后的功率譜

3 多通道ANC系統

由于單通道的ANC系統的降噪范圍有限，只能實現小范圍內的噪聲減小，而有源噪聲控制的目的是提高降噪效果，擴大降噪范圍以及適應復雜的環境，因此引入多通道控制系統進行降噪。多通道ANC系統與單通ANC系統類似[13]，有I個初始傳感器、J個次級聲源以及K個誤差傳感器、因此就存留了I×J個初級通道和J×K個次級通道。

本文將以1×2×2的雙通道有源降噪系統為模型，將分別對前文的FxLMS算法和改進的Fx-LMS算法進行分析和對比。

3.1 雙通道FxLMS算法

從以上分析可知，雙通道的系統模型1×2×2中，包含1×2個初級聲通道和2×2個次級聲通道，其示意圖[14]如圖7所示。P1(z)和P2(z)分別代表了初級傳感器到誤差傳感器1和誤差傳感器2的聲通道的傳遞函數，同理，S11(z)和S12(z)代表的是次級聲源1分別到誤差傳感器1和誤差傳感器2的次級路徑傳遞函數，S21(z)和S22(z)代表的是次級聲源2分別到兩個誤差傳感器的次級路徑傳遞函數。

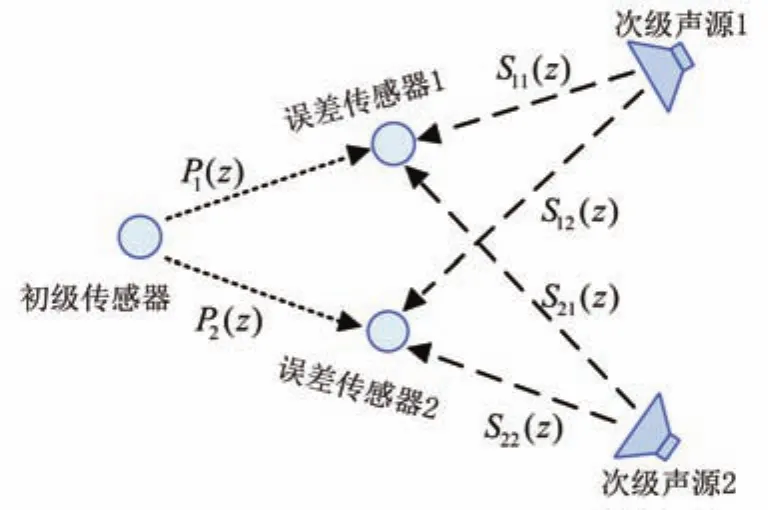
圖7 雙通道系統示意圖

圖8為基于 FxLMS算法的 1×2×2結構圖，圖中有只有一路的信號輸入，兩路次級信號的輸出和四路的次級通道，另外控制器的輸入信號是初始信號與四路次級通道傳遞函數估計值卷積運算后的信號，根據前文的單通道FxLMS算法的迭代過程可以寫出這個結構圖中的兩路誤差信號為：

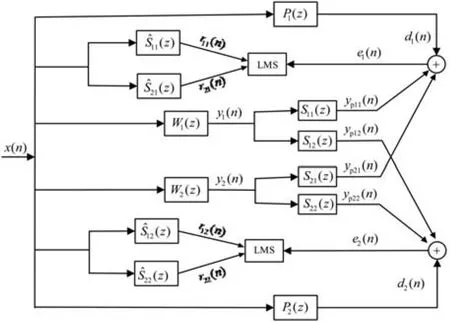
圖8 基于FxLMS算法的1×2×2結構圖

則兩個控制器權系數迭代公式為

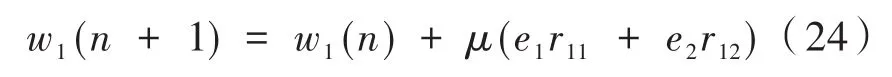
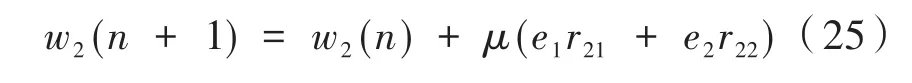
由式（24）和式（25）可知，在權系數迭代更新中每一個控制器都有兩個誤差量來共同調節，以此達到更好的降噪效果。

3.2 雙通道離線建模

雙通道系統與單通道系統相比，其系統的復雜度有所增加，如若采用在線建模的方式，稍有不慎就會造成整個系統的發散，此時離線建模的優點將更明顯地顯現出來，與在線建模相比，其算法的計算量大大減小，算法整體的運行速度和收斂收率也顯著提升，且有效地提高系統的穩定性。由于白噪聲的各頻段分量都是恒定的，因而它對次級通道進行建模而言是一種理想的激勵信號，并將獲得的次級通道估計值用于后續算法之中。

已知多通道系統中存留J×K個次級通道。而需要采用的FxLMS算法由于濾波信號的存在，則要求對所有的次級通道進行補償。因此離線建模需要的次級通道估計模型S?jk(z)也為J×K個。圖9給出了當J=2、K=2時的離線辨識算法結構[15]。

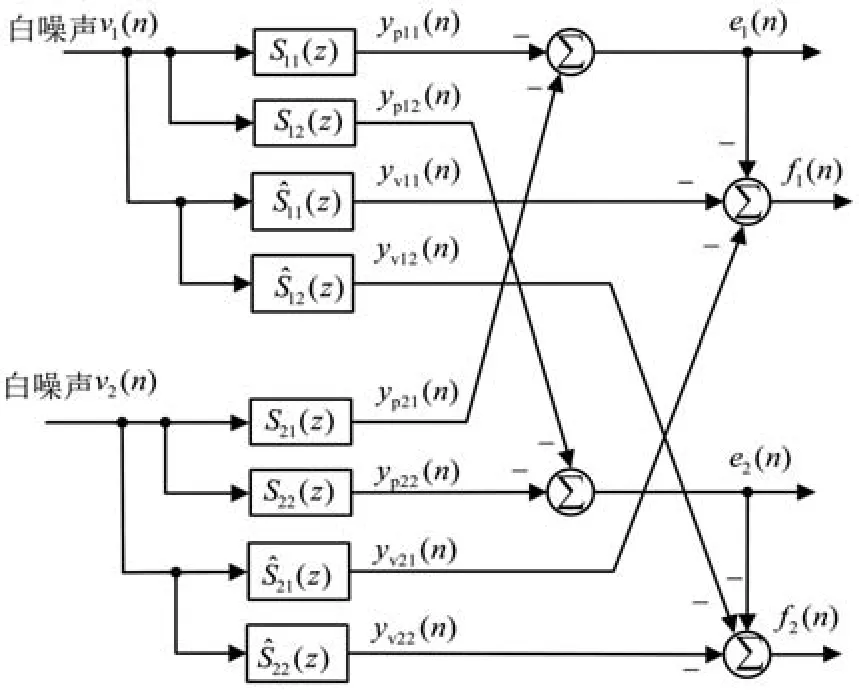
圖9 雙通道系統次級通道建模原理圖

其中v1(n)和v2(n)為雙通道離線建模系統輸入的白噪聲信號，另外，v1(n)、v2(n)經過次級通道估計模型S?jk(n)后輸出yvjk(n)，而v1(n)、v2(n)經過實際次級通道可輸出ypjk(n)，在誤差傳感器1和誤差傳感器2位置處，以上兩種次級聲源疊加可分別構成誤差信號e1(n)和e2(n)，其表達有：

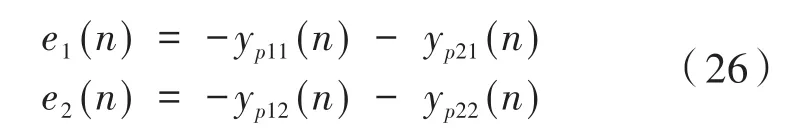
圖9中的f1(n)、f2(n)表示輸入信號經過次級通道和次級通道估計模型后輸出信號之間的差值，即：

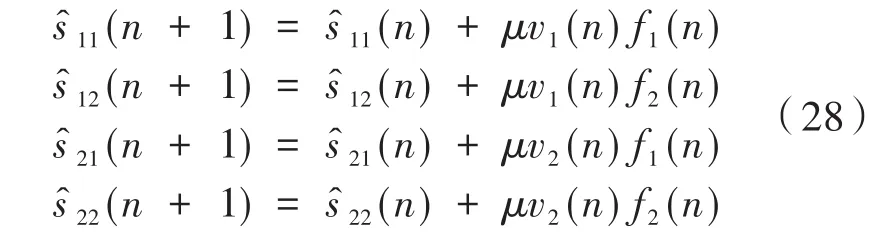
3.3 雙通道FxLMS仿真

（1）雙通道次級通路建模

在進行仿真前，需要完成上述原理圖中所有次級通道傳遞函的估計，根據文獻[16]，可設系統聲通道的傳遞函數，有：

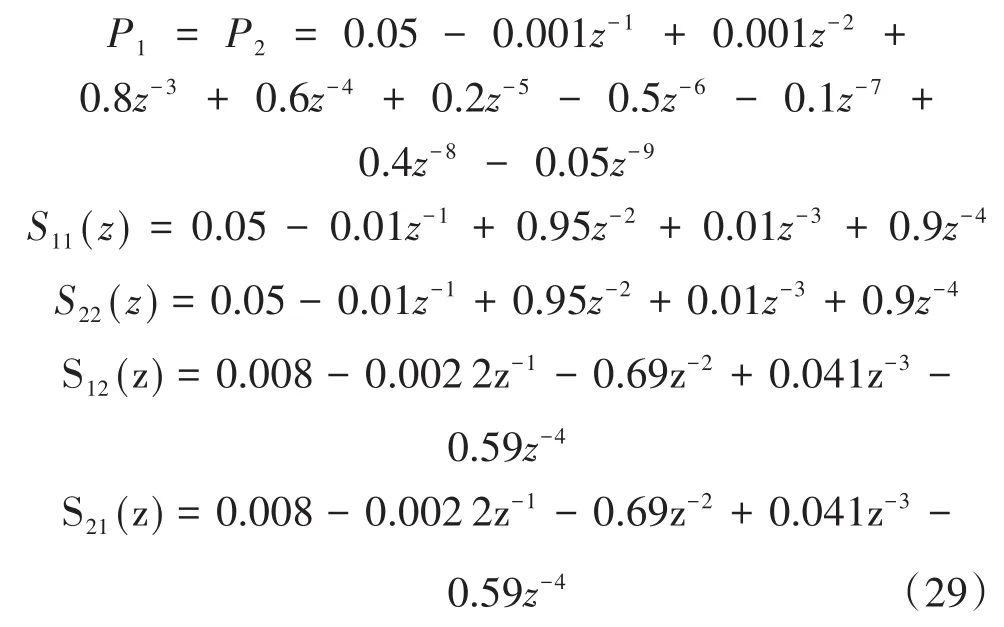
利用本節提及的白噪聲來檢驗上述次級通道傳遞函數的可行性，其中建模過程中算法的步長因子同樣為0.01，以次級通道1為例，其結果如圖10所示，即誤差信號可以很快地收斂于零，證明了所設置的次級通道傳遞函數是有效的，且不會造成系統的發散。

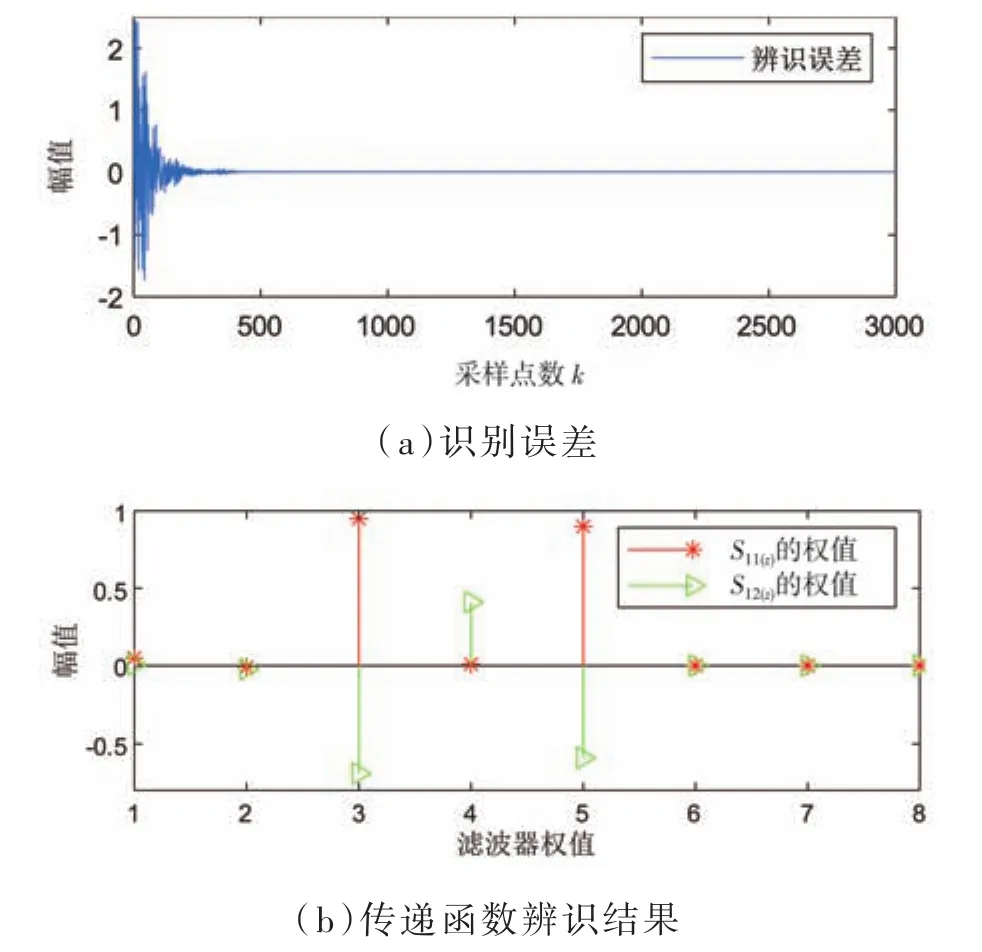
圖10 次級通路建模結果

（2）雙通道FxLMS算法仿真

仿真的信號參數和前文的單通道的參數一樣，則實驗仿真結果如圖11（a）和圖11（b）所示，在雙通道中，改進的FxLMS算法仍舊比傳統的FxLMS算法的收斂速度更快。

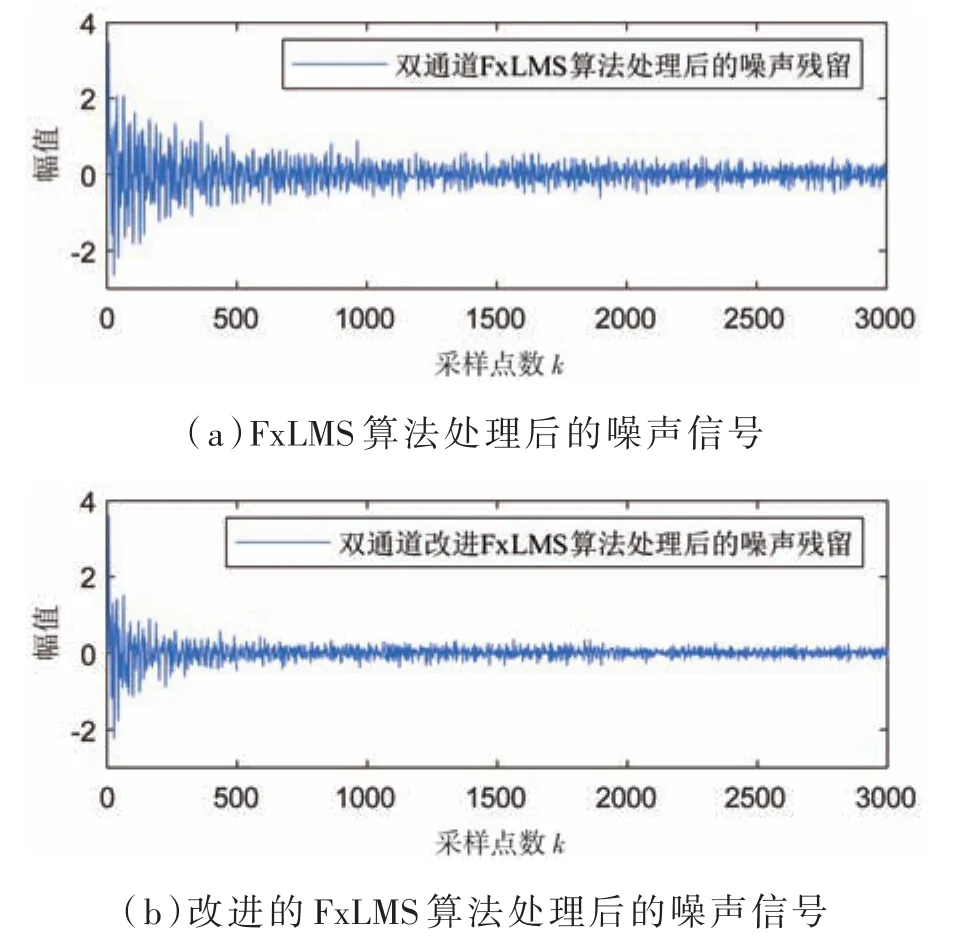
圖11 雙通道兩種算法的仿真結果

圖12是兩種算法在雙通道系統中降噪前后的功率譜。由圖12（a）圖可得，傳統FxLMS算法在降噪前后位于其中心頻率的降噪量達到為18.2 dB，由圖12（b）知，本文提出的泄露變步長FxLMS算法降噪前后在中心頻率處的降噪量最高達到24.7 dB。即雙通道比單通道的降噪效果好，且基于改進算法的降噪效果比傳統的FxLMS算法降噪效果好。

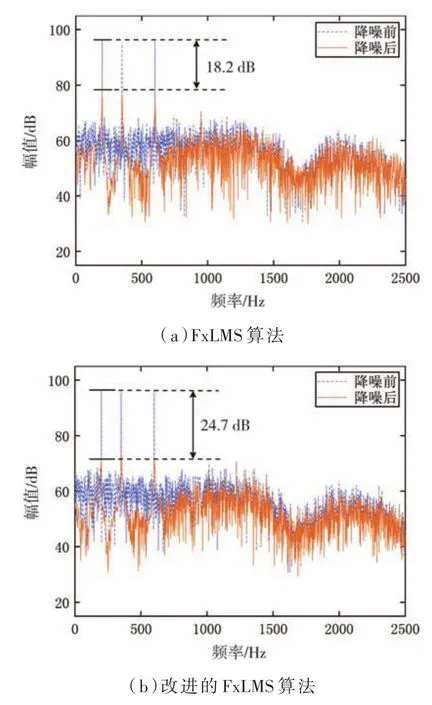
圖12 雙通道不同算法降噪前后的功率譜

4 結論

本文提出的泄露變步長FxLMS算法以瞬時誤差向量的平方值作為步長的函數的輸入信號，經仿真結果表明，在收斂速度和穩態誤差上均有明顯的優勢，并且其仿真功率譜表明，經過FxLMS算法和泄露變步長FxLMS算法降噪處理后，在單通道中的降噪量分別為13.8 dB和19.6 dB，而在雙通道中的降噪量分別為18.2 dB和24.7 dB，從雙通道ANC系統的降噪量可以表明多通道ANC系統有非常好的降噪效果。但是，對于多通道ANC系統而言計算量是未來進一步需要研究的重點。