車載部件振動特性研究

劉玄，陳立鋒，許芃芃

（1.411104 湖南省 湘潭市 湘潭理工學院 智能制造系；2.411201 湖南省 湘潭市 湖南科技大學 機電工程學院）

0 引言

汽車在行駛中，由于路面的不平整及發動機和傳動系統的激勵等都會引起汽車的振動，與此同時，車身和懸架的振動對座椅、中控臺等車載部件的疲勞失效以及鋼簧和阻尼器等部件的故障失效次數大幅增加，加大了對車輛行駛安全和乘坐舒適性影響。在汽車的振源中，路面的凹凸不平是主要因素，一般取路面激勵為隨機過程[1]。研究車輛在路面隨機激勵下的振動特性對車載部件的振動影響有一定的參考意義。

目前越來越多研究圍繞車載部件振動和受力特征及其對系統振動特征的影響展開。徐寧等[1]構建了由輪軌垂向激勵到系統部件位移和各作用力的傳遞函數，比較了不同模型下車輛各主要部件的位移幅頻傳遞特性以及各垂向作用力幅頻傳遞特征的差異，分析了一系列力作用點位置的改變對轉臂和車軸等部件的位移傳遞特征以及各懸掛力頻域傳遞特性的影響程度。Suarez 等[2]對比分析了不同懸掛參數下車輛的運用安全性、乘坐舒適性以及部件的疲勞失效等特征。唐卓[3]建立懸架座椅的結構模型,建立Simulink 模型,通過計算分析求得懸架座椅系統各組成部分之間的關系和運動狀態。Sumit[4]對汽車座椅的固有頻率進行了分析。使用NASTRAN 求解器進行了模態分析，對各部件分別進行了自由振動分析。姜繼瑜等[5]根據機組振動理論與工程實際，通過試驗與有限元分析相結合的方法對柴油發電機組的振動特性進行研究。Liang 等[6]提出十四自由度多體動力學模型，該模型的仿真值與試驗值有很好的吻合，用來研究不同坐姿下受垂直振動時的動力學響應。Javad[7]通過研究有背支撐狀態和無背靠背狀態的人體坐姿的垂直振動建立了兩種動力學模型：一是優化的五度自由度模型，可向一個方向顯示垂直振動；二是矩陣模型，利用剛度和阻尼矩陣呈現垂直振動的兩個方向：垂直和水平，并且對比了這兩種模型的優缺點。Zhu 等[8]利用歐拉法建立了駕駛員座椅動態舒適性模型，并根據控制理論建立狀態矩陣方程，利用MATLAB 模擬動態模型的運動。闕曉宇[9]利用牛頓法建立某汽車八自由度振動模型。分析整車動態時域響應特性，研究車身質心位置、懸架剛度、輪胎剛度和懸架阻尼等因素對駕駛員與車身質心處舒適性的影響。Lee 等[10]從理論和實驗兩方面研究了六缸柴油機與測功機連接的撓性聯軸器的扭轉振動和動態扭矩。陳學文等[11]采用模糊控制技術,結合PID 控制理論,以整車七自由度主動懸架為研究對象，利用Simulink 構建七自由度主動懸架仿真模塊，實現時域響應仿真。王娟等[12]建立了獨立懸架汽車整車七自由度動力學模型,推導了振動微分方程，運用數值仿真的手段研究了汽車懸架阻尼系數、剛度等設計參數對汽車振動特性的影響規律。張功學[13]為分析和提高轎車的乘坐舒適性，建立了轎車十一自由度動力學模型，利用濾波白噪聲法及傳遞函數法，建立路面隨機激勵的時域模型，利用Simulink 建立人—車—路系統仿真模型，對轎車在不同車速下不同位置的人體振動響應進行了仿真分析。

以上研究者都對某些車載部件的動力學特性以及整車的動力學特性進行了深入的研究，但是并沒有建立綜合考慮車載部件和整車的動力學模型，并不能完全反映出車輛在行駛時的振動對車載部件的影響。本文利用集中質量法，考慮車載部件的振動特性，建立了整車及車載部件的十自由度動力學模型，利用MATLAB/Simulink 對模型進行了仿真分析，得到了車載部件在車輛行駛過程中的動力學特性，分析對比了車身質心處和車載部件的垂向振動特性以及車載部件側向和縱向的振動特性，對車載部件在車輛行駛過程中的振動特性研究有一定的參考意義。

2 動力學模型的建立

假定車身是一個剛體，采用集中質量法和動能不變原則，當車輛在水平面做勻速直線運動時，車身具有上下跳動、俯仰、側傾3 個自由度，獨立懸架的4 個車輪分別具有垂向運動的自由度，車載部件具有垂向、側向和縱向3 個自由度。圖1為汽車十自由度整車振動模型。

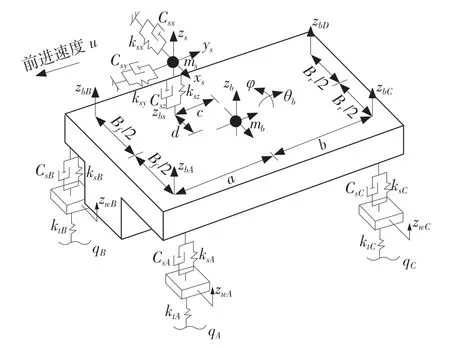
圖1 十自由度整車模型圖Fig.1 Ten-degree-of-freedom vehicle model diagram

設10 個自由度的振動位移分別為zb、θb、φ、zwA、zwB、zwC、zwD、zs、xs、ys，則系統的廣義位移列陣可表示為：

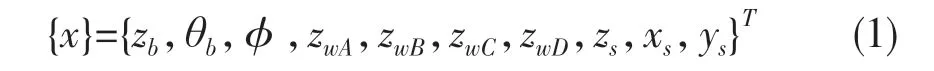
當俯仰角θb和側傾角φ較小時，車身4 個端點（A、B、C 和D）處的垂向位移的關系為[14]：

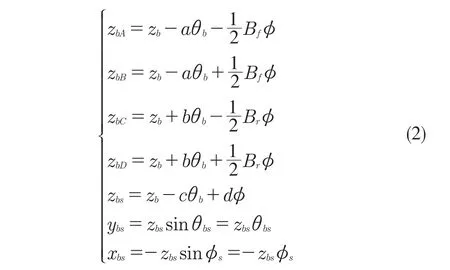
因此，車身質心處的垂向運動方程為：

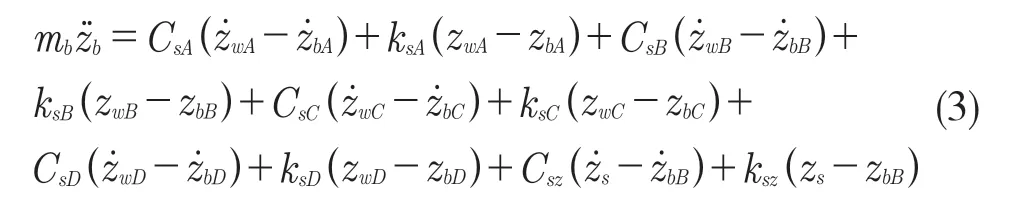
車身俯仰運動方程為：

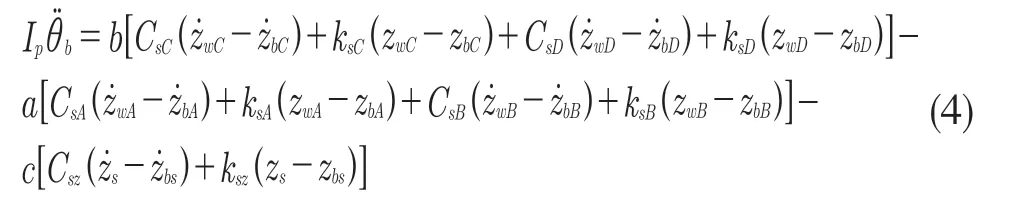
車身側傾運動方程為：

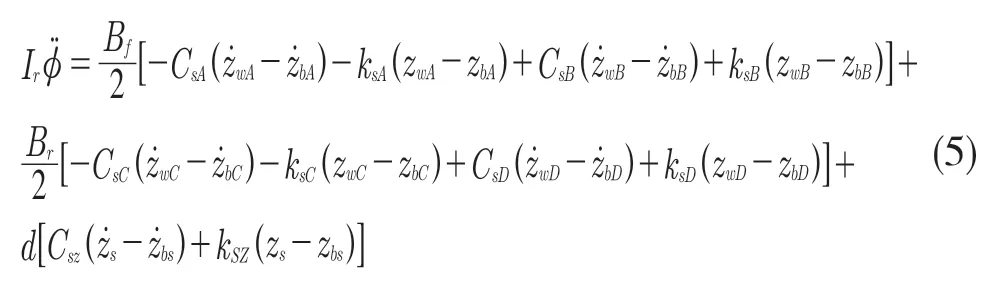
4 個非簧載質量的垂向運動方程分別為：

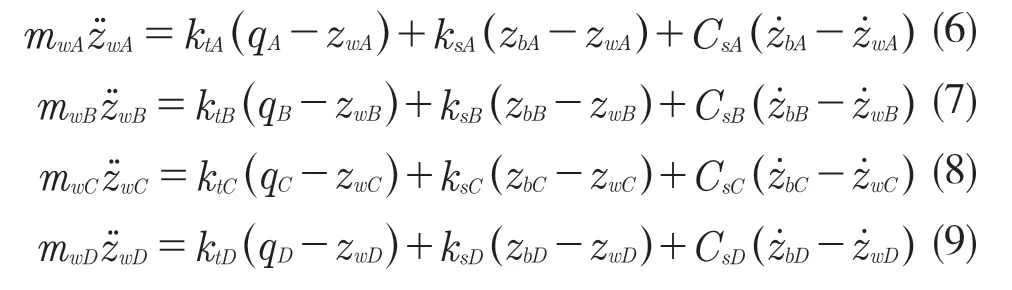
車載部件垂向振動微分方程為：

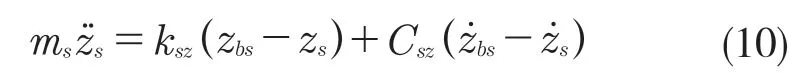
車載部件側向振動微分方程為：

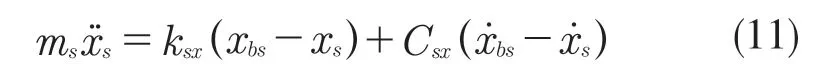
車載部件縱向振動微分方程為：

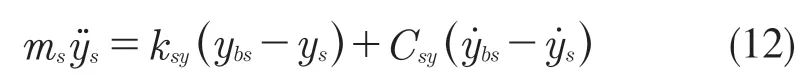
式（3）—式（12）10 個微分方程式[14]給出了十自由度整車動力學模型。

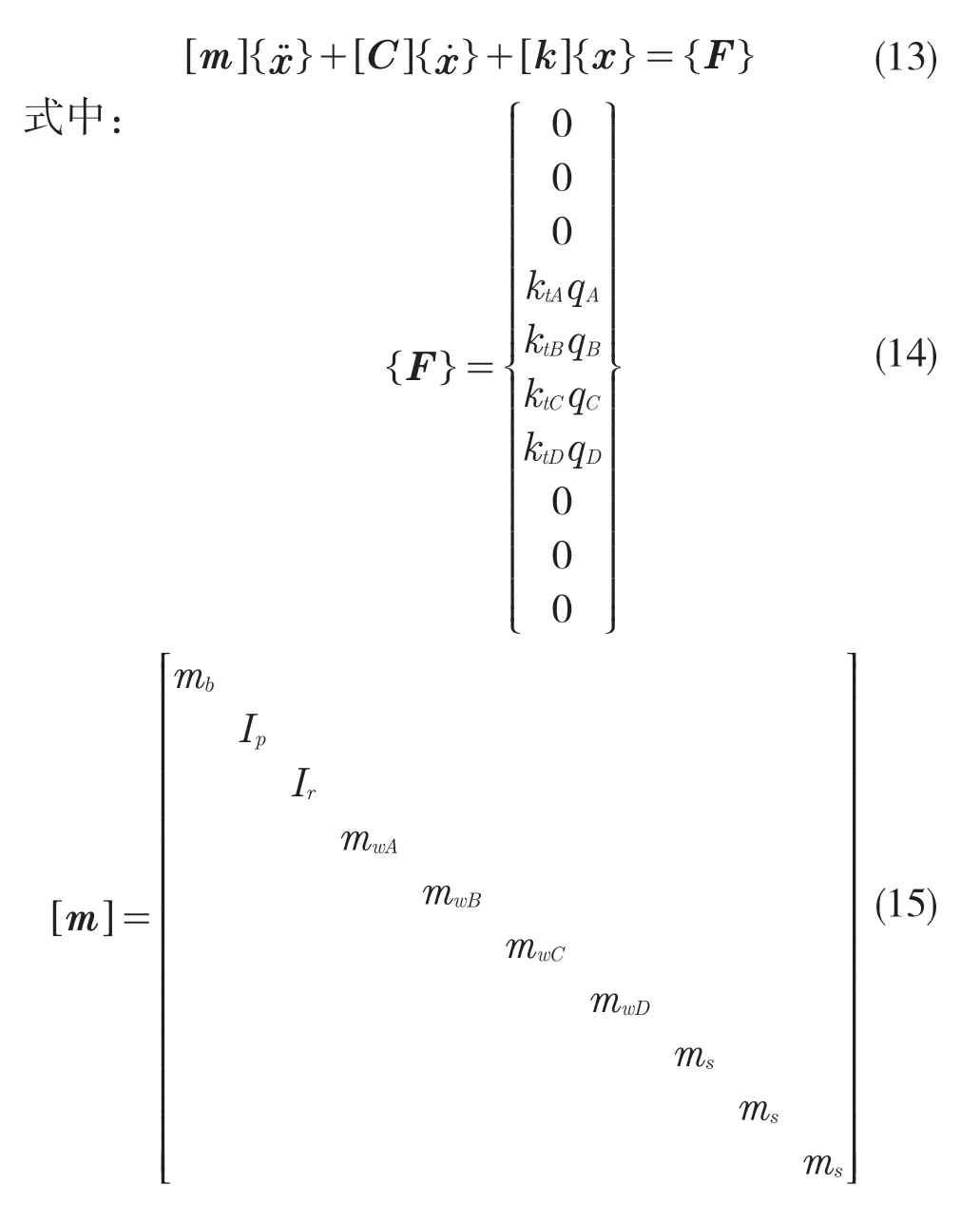
寫成矩陣形式，分析模型如式（13）。

2.2 路面激勵模型

根據GB 7031-86《車輛振動輸入路面平度表示方法》規定的路面功率譜密度的擬合表達式，參考文獻[15]采用1 階濾波帶限白噪聲的方法建立隨機路面激勵模型，模型為：

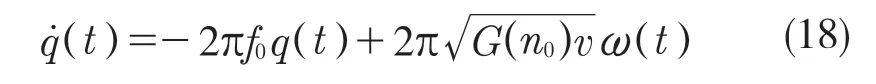
式中：f0——下截止頻率，取f0=0.062 8 Hz；q（t）——隨機路面激勵信號；G（n0）——路面不平度系數，對于仿真的B 級路面，G（n0）=6.4×10-5m3/cycle；v——車速，取仿真速度v=60 km/h，即v=16.7 m/s；ω（t）——均值為0 的高斯白噪聲信號。

路面激勵仿真模型如圖2 所示，得到的隨機路面激勵信號如圖3 所示。

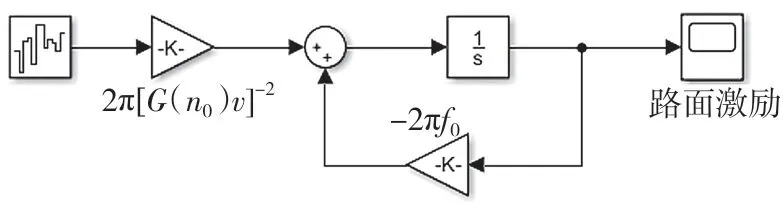
圖2 路面激勵仿真模型Fig.2 Simulation model of road excitation

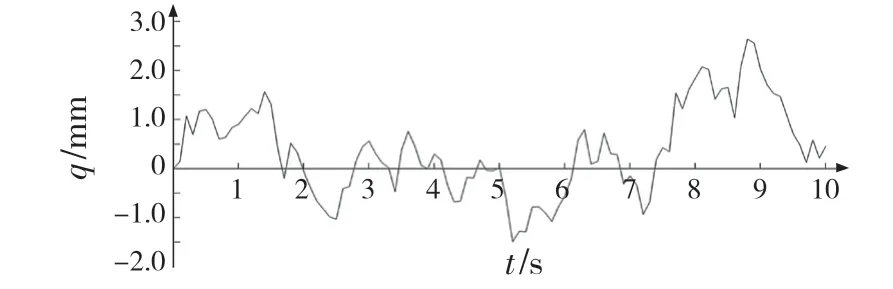
圖3 隨機路面激勵信號Fig.3 Diagram of random road excitation signal

3 實例分析

以某款國產車型為例，其具體參數如表 1 所示。根據表1 參數，本文選取汽車勻速直線行駛于良好道路，故取路面等級為B 級，車速為60 km/h，在 MATLAB/Simulink 中搭建系統模型，進行仿真分析，得到的仿真結果如圖4—圖9 所示。

表1 車輛參數表Tab.1 Vehicle parameters

圖4 表示車身質心處的垂向振動，由圖可知：當車輛在良好路面勻速直線行駛時，車身質心處的垂向振動整體波動范圍并不大，圖4 中振動位移zb變化在3 mm 范圍內。

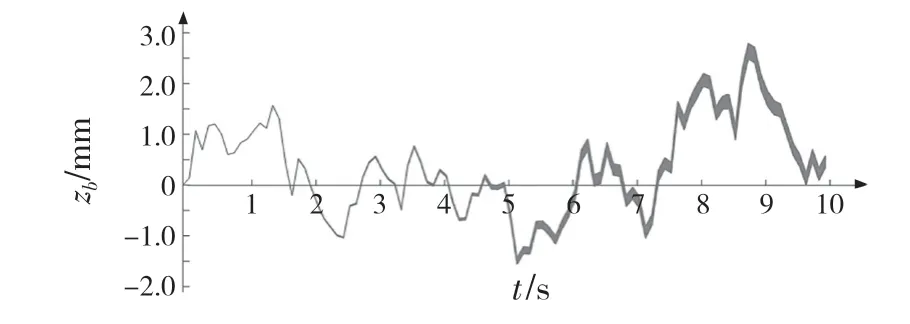
圖4 車身質心處垂向振動Fig.4 Vertical vibration at vehicle body centroid

圖5 表示車載部件垂向振動，圖中車載部件的垂向振動整體波動范圍并不大，振動位移zs變化在1.5 mm 范圍內。

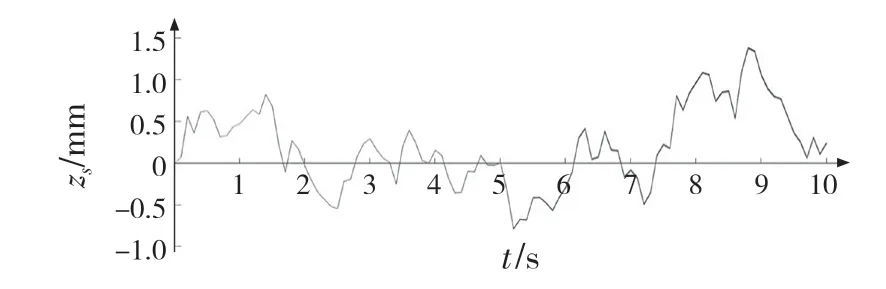
圖5 車載部件垂向振動Fig.5 Vertical vibration of vehicle-mounted part

圖6 為車身質心處和車載部件垂向振動的對比圖，由圖6 可知：對車輛本身而言，其質心處的垂向振動位移最大幅值是3.0 mm，而車載部件的垂向振動位移最大幅值是1.5 mm，比車身質心處的最大幅值小了一半，由此看出，當車輛在良好路面勻速直線行駛時，車載部件隨著車身的振動而振動，但其振動幅度比車身質心處的要小。

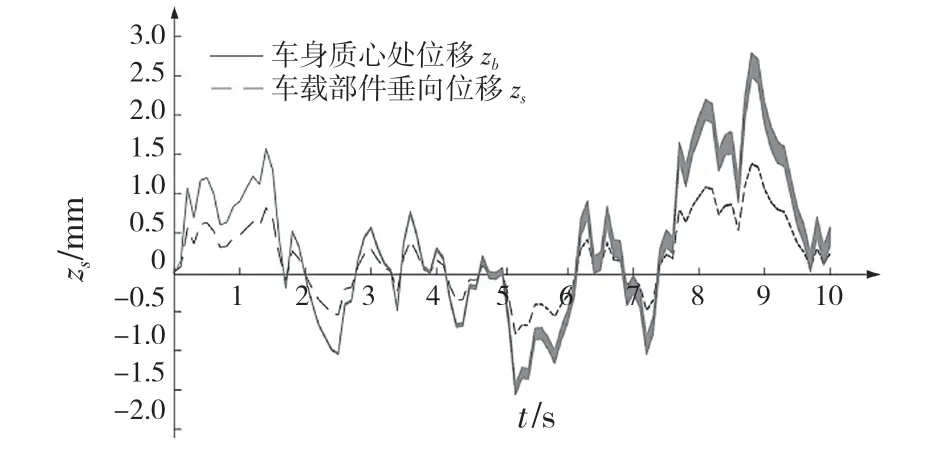
圖6 車身質心處和車載部件垂向振動對比圖Fig.6 Comparison between vertical vibration of vehicle body centroid and vehicle-mounted part

圖7、圖8 為車載部件側向和縱向振動位移，可知：當車輛在良好路面勻速直線行駛時，車載部件縱向振動的振幅較小，最大幅值為0.03 mm；相比于縱向振動，車載部件在側向受到的振動更小，僅為縱向振動的一半，其最大幅值為0.015 mm。

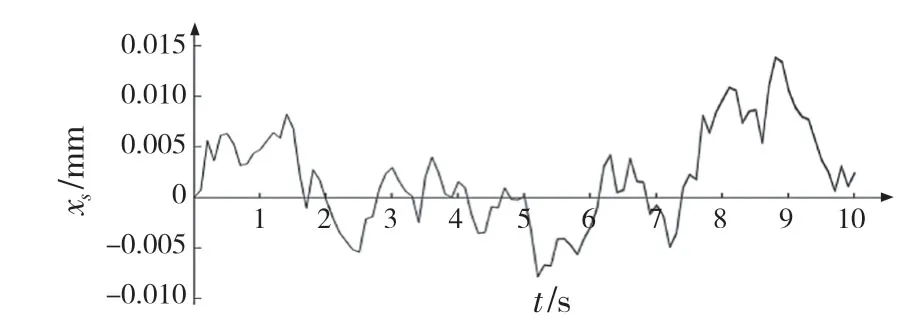
圖7 車載部件側向振動Fig.7 Lateral vibration of vehicle-mounted part

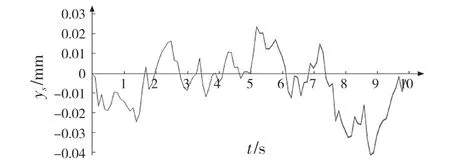
圖8 車載部件縱向振動Fig.8 Longitudinal vibration of vehicle-mounted part

圖9 表示車載部件在垂向、側向和縱向振動位移的對比圖，由圖9 可見，車載部件在側向和縱向的振動位移幅值相近，而與垂向振動之間存在差異，其中側向和縱向的振動位移幅值在0.03 mm 以內，而垂向振動位移的幅值在1.5 mm 以內，比側向和縱向的振動位移大了50 倍。

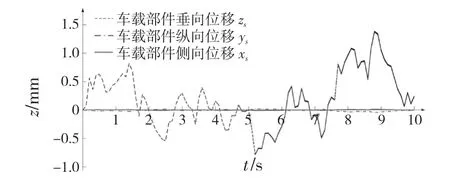
圖9 車載部件垂向、側向、縱向振動對比圖Fig.9 Vertical vibration,lateral vibration and longitudinal vibration of vehicle-mounted part

4 結論

本文通過建立考慮車載部件的十自由度動力學模型，利用Simulink 對模型進行仿真分析，對車輛在良好路面勻速直線行駛時車載部件的振動特性進行了分析，得到以下結論：

（1）車載部件在車輛行駛過程中的動力學特性：當車輛在良好路面勻速直線行駛時，車載部件的振動位移整體波動較小，但與側向和縱向的振動位移相比，垂向振動的幅值更為明顯，其最大振動幅值遠大于側向和縱向的振動幅值。

（2）對比車身質心處和車載部件的垂向振動特性：當車輛在良好路面勻速直線行駛時，車載部件隨著車身的振動而振動，但其振動幅值比車身質心處的振動要小。