基于改進殘差網絡的雷達輻射源信號識別

郭恩澤，張洪德*，楊 雷，劉益岑，彭鏡軒，張 磊

(1.中國人民解放軍陸軍工程大學 通信士官學校，重慶 400035；2.中國人民解放軍陸軍工程大學 通信工程學院，江蘇 南京 210007；3.信號盲處理國家級重點實驗室，四川 成都 610041)

0 引言

雷達輻射源識別是實施雷達對抗的前提和基礎，是在雷達信號截獲、分選的基礎上，通過分析雷達信號的工作參數和特征參數，利用這些參數推斷該雷達的體制、用途、型號、威脅等級和部署地點等信息，為己方進行電子對抗決策提供重要的情報支撐，其識別水平是衡量雷達對抗設備技術先進程度的重要標志[1]。隨著電磁環境的信號日趨密集、雷達體制的多樣化及普遍存在的噪聲等影響，傳統的參數匹配法[2]和通過將信號進行時域[3]、頻域和時頻域[4]等變換，然后人工提取脈內特征進行分類識別的方法，存在低信噪比下識別率低[5]、泛化能力弱[6]和魯棒性差等缺點。

當前，深度學習方法在圖像分類[7]、計算機視覺[8]和語音識別[9]等方面取得了矚目的成績，國內外學者逐漸開始利用深度學習的方法進行雷達輻射源識別的研究[10]。其中，典型的深度學習模型是卷積神經網絡(Convolutional Neural Network，CNN)，利用CNN在解決計算機視覺任務上的強大性能，對雷達輻射源信號進行一定的變換，提取其二維圖像特征(較為常用的是時頻分布特征)作為樣本訓練CNN模型，然后進行分類識別[11]。文獻[12]首先將雷達信號變換為雷達時頻圖像，然后利用設計的CNN對時頻圖進行分類識別，在信噪比為-8 dB條件下，對8種雷達信號的識別率可以達到98.31%。相比于結構簡單的的網絡模型，AlexNet[13]，VGGNet[14]，GoogLeNet[15]等網絡模型有著高效的結構設計、提取更多特征的深層結構及成熟的性能，在ImageNet比賽中均取得了優秀的成績。部分學者開始利用這些網絡模型進行雷達時頻圖像識別，文獻[16-18]利用AlexNet模型對雷達輻射源信號、雷達干擾信號和低截獲概率雷達信號進行分類識別，取得了良好的識別率，比采用非深度學習的分類方法和利用LeNet5 CNN模型分類的方法識別效果更好、抗噪性能更強。文獻[19]利用VGGNet模型對5種雷達輻射源信號進行分類識別，在信噪比為-12 dB的噪聲條件下，識別率達到90%。文獻[20]利用GoogLeNet的預訓練模型對窄帶雷達群目標進行識別，在小樣本條件下取得了較高的識別率。近年來，為了提高識別速度，方便網絡模型在便攜設備上應用，輕量級神經網絡以其高效的網絡計算方式成為研究的熱點[21]，2016年—2019年，輕量化的CNN SqueezeNet，MobileNetV2[22]等模型相繼被提出。文獻[23]設計了輕量級神經網絡對8種電磁調制信號進行識別，在信噪比為-6～6 dB的噪聲條件下獲得96.1%的綜合識別率。

上述方法從不同的角度進行了探索，其主要研究不足在于：為了提取更為復雜的目標特征，上述網絡模型都有著較深的網絡層數和較大的參數量，不可避免地帶來了梯度傳播時的消失或者爆炸現象，會導致網絡誤差不斷增大，網絡的識別正確率出現飽和甚至是下降的現象。殘差網絡通過在前向神經網絡上增加一個跳躍從而繞過一些網絡層，實現快捷連接，解決了以上問題。因此，本文在分析雷達信號時頻圖特性的基礎上，借鑒輕量化[21-23]和圖像識別相關研究[24]的網絡設計思想，設計一種以殘差網絡為主體結構[25]的改進殘差網絡模型，該模型兼顧了性能和復雜度。

1 雷達信號模型與時頻分析處理

在高斯白噪聲環境下，偵察接收機接收雷達信號的模型可表示為：

x(t)=s(t)+n(t)，

(1)

式中，s(t)為雷達信號；n(t)為高斯白噪聲。

雷達信號s(t)又可以表示為：

s(t)=Ae{j[2πf0 t+φ(t)+φ]}，

(2)

式中，A為輻射源幅度；f0為輻射源信號載頻；φ為初始相位；φ(t)為脈內調制信息。輻射源的特征差異集中體現在φ(t)，本文主要考慮7種調制方式:常規脈沖信號(CW)、線性調頻信號(LFM)、非線性調頻信號(NLFM)、二相編碼信號(BPSK)、四相編碼信號(QPSK)、二相頻率編碼信號(BFSK)以及四相頻率編碼信號(QFSK)。

傳統的信號處理中，主要是在時域和頻域分析信號。信號的時域表示信號隨時間的變化關系，信號的頻域表示信號在整個時間內的全部頻譜成分。因此，時域和頻域分析并不能揭示頻率隨時間的變化關系。時頻分析能夠同時在時域和頻域描述信號，將一維的時域信號轉化為二維的時間和頻率密度函數，揭示了信號能量隨時間和頻率的變化關系，有助于在信號識別時提取更多的信號特征。本文利用短時傅里葉變換(STFT)作為時頻分析的方法，給定一個信號s(t)，其短時傅里葉變換可定義為：

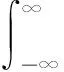
(3)

式中，h(t)為加窗函數。可以看出，變換域同時涵蓋了時間和頻率的調制信息，而且可以利用深度CNN對圖像識別的強大功能處理二維時頻圖。

信噪比為0 dB時，7類雷達信號的時頻分布圖像圖如圖1所示。可以看出，BPSK，CW，LFM能量分布比較特殊，與其他信號差異明顯，而其他4種信號時頻圖像特征在一定程度上被噪聲“淹沒”，尤其對于相似度較高的BFSK，QFSK信號，當信噪比較低時，識別容易產生混淆。

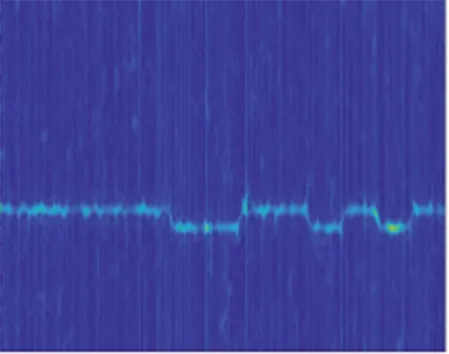
(a) BFSK

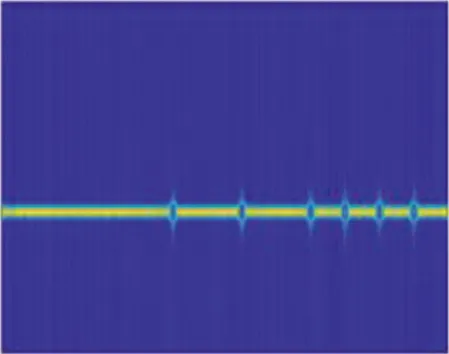
(b) BPSK

(c) CW

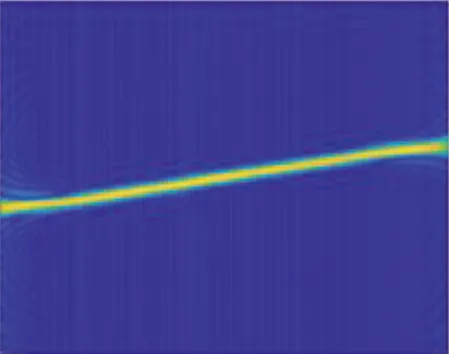
(d) LFM

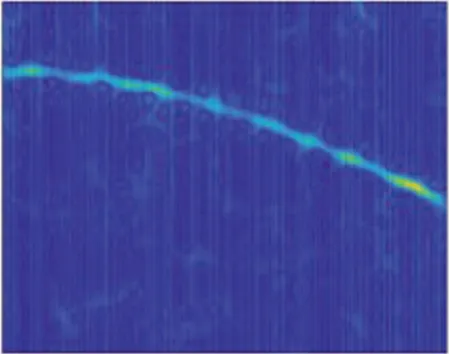
(e) NLFM

(f) QFSK

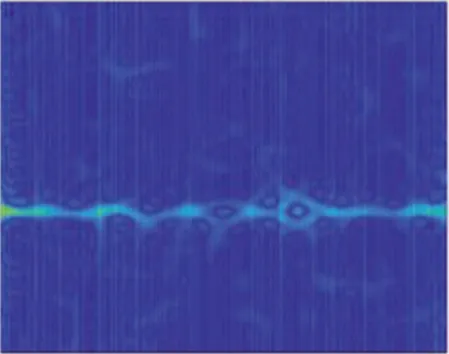
(g) QPSK圖1 7類雷達信號的STFT時頻分布Fig.1 STFT time-frequency distribution of seven types of radar signals

2 基于改進殘差網絡的雷達輻射源識別

2.1 CNN訓練理論推導

CNN的訓練過程是構建代價函數，通過學習來找到最合適的權重和偏置，使得代價函數接近最小值。其中，梯度下降法是該過程的核心，梯度就是函數上升最快的方向，要使代價函數下降最快，應沿著梯度的反方向[26]。

假設輸出類別為N，第i個輸出可表示為卷積核的權重w和卷積核的偏置b的函數zi(w,b)，經過激活函數f后的輸出ai(w,b)可表示為:

ai(w,b)=f(zi(w,b))。

(4)

假設各學習數據輸出對應的正確解為ti，總共有M個訓練樣本,則第k個訓練樣本圖像的平方誤差函數Ck可表示為：

(5)

利用全體訓練樣本的平方誤差總和構建代價函數C：

(6)

根據代價函數，梯度下降法的數學表示為：

(7)

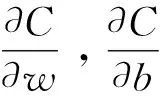
在誤差反向傳播算法中引入神經元輸出誤差δi的概念，δi可表示為：

δi=(ai-ti)f′(zi)。

(8)

根據δi可以求出：

(9)

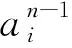
由式(7)～式(9)可知，僅需要計算出輸出層的神經元誤差，然后通過將誤差一層一層反向傳播，可以計算出其他神經元誤差，進而計算出下降梯度，更新網絡模型中的參數值。誤差反向傳播算法確定CNN參數的流程如圖2所示。

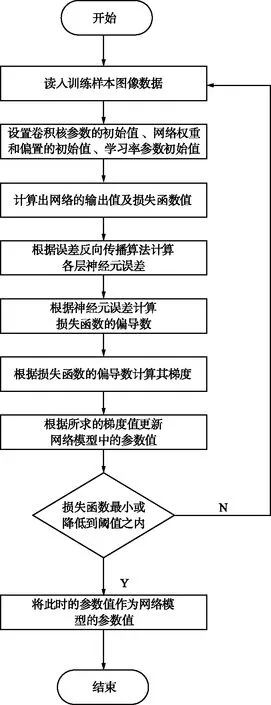
圖2 誤差反向傳播算法確定CNN參數的流程Fig.2 Flow chart of error backpropagation algorithm to determine parameters of CNN

2.2 殘差網絡原理

自AlexNet之后，CNN層數不斷加深，網絡擬合能力越來越強，但網絡的識別率卻趨于飽和，甚至有下降的趨勢，訓練誤差也不再減小。分析原因：一是由于深度網絡不易優化，有效信息難以被直接利用；二是由于反向傳播的梯度計算是在上一層基礎上進行的，網絡深度加深會使梯度復乘，使梯度在多層反向傳播時越來越小，最終導致梯度消失。

殘差網絡基于殘差結構的設計，實現快捷連接(Shortcut Connection)，解決了以上問題。殘差網絡模塊如圖3所示，假設CNN某一層輸入為X，在經過網絡傳輸處理之后，得到的期望輸出為H(X)。殘差模塊的引入改變了網絡學習目標，使其不再學習一個完整的輸出H(X)，而是學習輸出與輸入之間的差別，即殘差F(X)：

F(X)=H(X)-X。

(10)

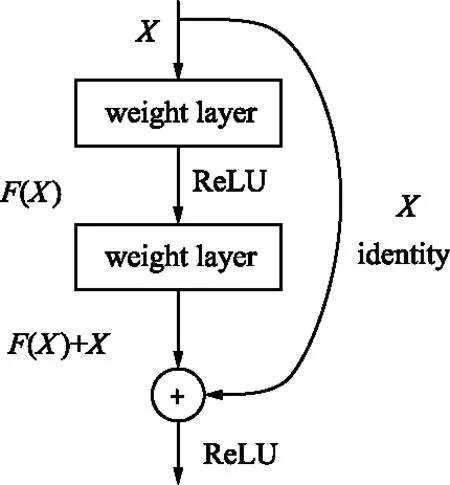
圖3 殘差網絡模塊Fig.3 Residual network module

當網絡達到某一個深度時，如果網絡的訓練已經達到最優狀態，此時的錯誤率最低，再往下加深，網絡會出現退化問題。此時,X就是最優輸入，接下來僅需要建立恒等快捷映射(H(X)等于X)，令F(X)等于0即可，這樣網絡深度增加，訓練誤差也不再上升。

當上下2層的通道數不一致時，即輸出F(X)與X維度不一致，可以在做快捷連接時，對X做一定的線性變換，此時H(X)可表示為：

H(X)=F(X)+W*X，

(11)

式中，W為卷積操作，在實際模型中，通常用1×1的卷積核進行升維或者降維操作，以便和F(X)保持維度一致。

2.3 改進殘差網絡模型設計

2.3.1 改進殘差網絡模型設計方法描述

殘差網絡由于其獨特的快捷連接設計，在一定程度上保證了信息的完整性，解決了傳統卷積在信息傳遞時出現的信息丟失和損耗問題，避免了由于網絡過深導致的性能下降問題，進一步提高了對目標的分類識別率。因此，本文選擇殘差結構為主體，設計適合雷達信號識別的深度學習網絡模型。

目前，殘差網絡模型共有5種不同的深度，分別是：ResNet18，ResNet34，ResNet50，ResNet101，ResNet152，模型后面的數字代表殘差模型的網絡深度。有研究表明，殘差網絡的效果類似于不同深度網絡模型的集成。因此，在一定程度上，隨著殘差網絡模型的深度增加，其性能也越來越好。然而，上述模型在追求性能的同時，模型規模和計算量也成倍增長，很難取得性能與復雜度的雙重提升。深入分析發現，由于殘差結構的優越性，殘差網絡深度相對較淺時，隨著模型深度的增加，模型性能提升幅度較大，當模型深度達到一定程度之后，再增加深度，模型性能提升幅度較小，并逐漸趨近于飽和。例如，文獻[25]利用ImageNet數據集對上述殘差模型進行訓練和測試，結果表明，34層的殘差模型比18層的殘差模型錯誤率低3.3%；50層的殘差模型比34層的殘差模型錯誤率低1.7%；152層的殘差模型比50層的殘差模型錯誤率低1.4%。因此，需要根據所要識別目標，設計合適的殘差模型深度，平衡模型性能和復雜度。

雷達輻射源信號時頻圖不同于實際生活中的圖像數據，與真實圖像相比，細微特征不夠豐富、表達特征的信息相對較少、圖像質量較差，而目前的殘差網絡模型主要針對真實圖像設計。因此，需要根據雷達信號時頻圖的特點，選擇合適的殘差模型體量以及輸出維度。

與此同時，文獻[24]對殘差網絡進行深入研究，通過可視化分析和實驗結果發現，最大池化層(Maxpoling)會導致高幅度高頻率的激活值，增加網格(Gridding)效應。為了進一步提升網絡模型性能，使用卷積層替代最大池化層。本文設計改進殘差網絡模型也借用這一設計思想。

2.3.2 改進殘差網絡模型框架

綜上分析，本文設計了一種改進的殘差網絡模型，采用文獻[25]提出的殘差網絡主干結構，與文獻[25]模型框架對比如表1所示。由5個卷積部分、一個最大池化層、一個全局平均池化層(Average Pool)和一個全連接層構成。5個卷積部分構建殘差連接，conv2_x～conv5_x的殘差連接輸入與輸出維度不匹配，需采用1×1卷積核對輸入特征圖進行升維。為了提升模型的訓練速度，有效緩解梯度彌散、消失等問題，各個卷積層進行非線性激活操作之前，先進行批量標準化操作，即增加一個BN(Batch Normalization)層[27]。

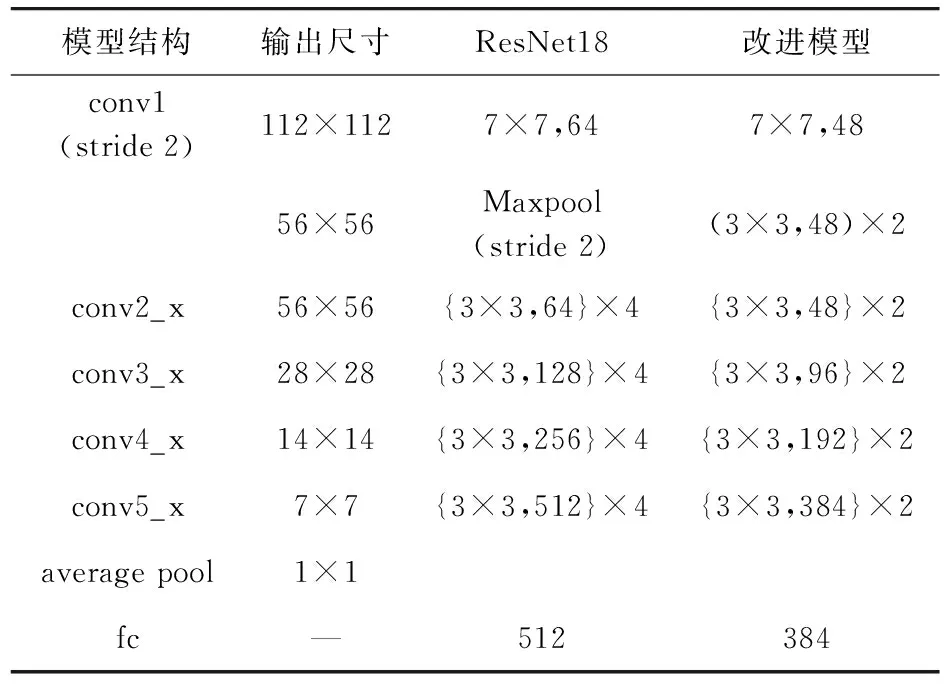
表1 改進殘差網絡模型與ResNet18結構對比Tab.1 Comparison between improved residual network model and ResNet18 structure

與文獻[25]所設計的殘差網絡模型ResNet18相比，本文改進后的殘差網絡模型有以下幾點創新：① 精簡網絡模型深度。ResNet18模型conv2_x～conv5_x卷積部分共有16個卷積層，精簡后的模型conv2_x～conv5_x卷積部分僅有8個卷積層。② 壓縮特征圖維度。ResNet18模型conv1～conv5_x卷積部分輸出特征圖維度分別為64，64，128，256，512。改進后的模型conv1～conv5_x卷積部分輸出特征圖維度分別為48，48，96，192，384，是原來維度大小的75%，相應地，輸入softmax分類器的特征維度也得到同等程度的降低。③ 利用2個3×3卷積層代替ResNet18模型的最大池化層。2個3×3卷積層均不進行激活和批量歸一化操作，具備一定的濾波作用，減少網格效應[24]。

改進后的模型通過優化設計殘差網絡模型的結構，使其擁有更為強大的特征提取性能。同時，結合雷達時頻圖像特點，精簡網絡模型深度和輸出特征圖維度，在一定程度上可以緩解“過擬合”問題和用于分類的特征維度過高導致的“維度災難”問題[7]。

對比分析來看，改進后的殘差網絡模型深度低于ResNet18模型，可能導致識別性能有輕微下降，但是，改進后的網絡通過優化輸出特征圖維度和減少網格效應的操作，會進一步提升模型性能。綜合分析，改進后的殘差網絡模型性能應該接近ResNet18模型。但是，改進后的殘差網絡模型在參數量和網絡復雜度等方面遠低于ResNet18模型，相應的時效性也遠勝于ResNet18模型[23]。查看Matlab軟件生成的2種模型規模，ResNet18模型規模大小約為40.2 Mb，本文改進后的殘差網絡模型規模大小約為10.1 Mb，約為ResNet18模型規模的25.1%。

3 仿真實驗與分析

為了驗證本文改進殘差網絡模型的性能，從識別率驗證、識別魯棒性驗證2個方面設計仿真實驗并進行分析。實驗均在Matlab2020b平臺上完成，仿真環境搭載Intel Core i7 2.8 GHZ處理器，操作系統為Windows10專業版64位。

3.1 雷達信號仿真參數設置

仿真第2節所述的7種常見的雷達輻射源信號，信號載頻為40 MHz。其中，BPSK和BFSK均采用13位的巴克碼，QPSK和QFSK編碼序列長度為6，LFM調頻斜率為20 MHz/μs，NLFM調頻指數為500，BFSK的2個頻率分別為35，40 MHz，QFSK的4個頻率分別為35，40，50，60 MHz。在-15～0 dB信噪比(步長為1 dB)條件下隨機生成訓練樣本，每個信噪比對應100×7個樣本，共計11 200個訓練樣本。隨機選取70%的訓練樣本作為網絡訓練的訓練集，30%的訓練樣本作為網絡訓練的驗證集。在同樣的信噪比條件下隨機生成測試樣本，每個信噪比對應50×7個樣本，共計5 600個測試樣本。所有樣本利用Matlab中的批量調整圖像數據的augmentedImageDatastore函數，將樣本尺寸調整成與各網絡模型輸入尺寸相匹配。

3.2 不同網絡模型識別率對比

CNN對雷達信號時頻圖像的識別流程如下：首先，將圖像數據集分成訓練集、驗證集和測試集；其次，利用訓練集和驗證集完成網絡模型的學習訓練；最后，利用訓練好的模型對測試集中的樣本進行識別率測試實驗。

為了驗證本文提出的改進殘差網絡模型性能，本次實驗設計實驗組和對照組。利用文中改進殘差網絡模型進行雷達輻射源信號識別為實驗組。文獻[25]提出了ResNet18模型，利用該模型進行雷達輻射源識別，以此為對照組1；文獻[15]提出了GoogLeNet模型，以此為對照組2；文獻[22]提出了MobileNetV2模型，以此為對照組3；文獻[18]提出了的利用AlexNet模型進行雷達輻射源識別，以此為對照組4。訓練參數均設置如下：初始學習率為0.001，最大訓練輪數為8，學習率減小因子為0.5，減小學習率的周期間隔為1，其他訓練參數設置均為默認值。

利用各訓練好的模型對測試集進行分類識別，在-15～0 dB信噪比條件下的綜合識別率對比如表2所示。本文改進殘差網絡模型識別率為95.9%，與ResNet18識別率接近，比MobileNetV2高約1.4%，比AlexNet高約3.1%，比GoogLeNet高約5.6%。這說明具有殘差結構的網絡模型性能優越，以殘差網絡為主體結構設計網絡模型具有科學性，因此，本文提出的改進殘差網絡模型對7種雷達信號具有較高的識別率。

表2 各類網絡模型綜合識別率對比Tab.2 Comparison of comprehensive recognition rates of various network models

3.3 不同網絡模型魯棒性對比

魯棒性驗證包括2種實驗：一種是低信噪比條件下的識別率對比；另一種是低信噪比條件下不同信號的識別率對比。

各模型在不同信噪比條件下的識別率對比如圖4所示。隨著信噪比的提高，各網絡模型對雷達輻射源信號的識別率不斷提高，當信噪比大于-5 dB時，各網絡模型的識別率均為100%。對比來看，在任意信噪比條件下，改進殘差模型對7類信號的識別率接近ResNet18模型，均高于其他3種模型，而且信噪比相對越低，識別率高的幅度相對越大。這說明改進后的殘差網絡模型在低信噪比條件下對7種雷達信號的依然具有較高的識別率。

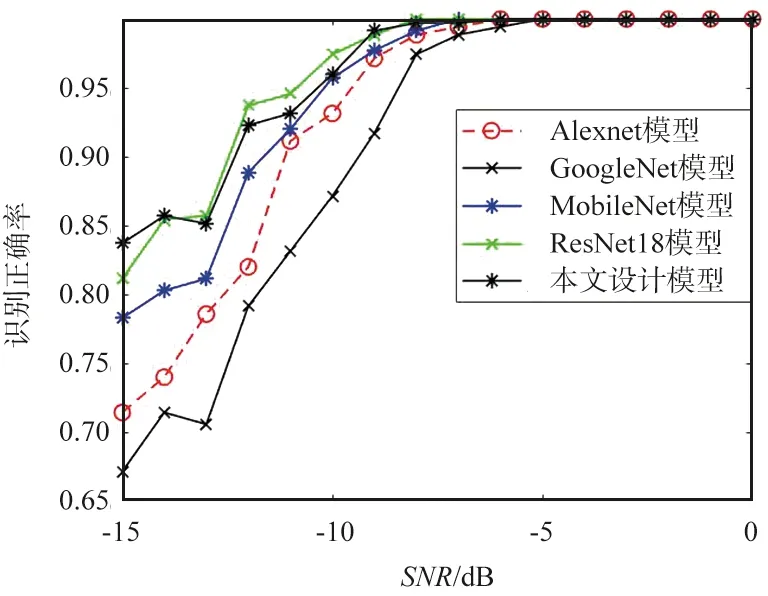
圖4 各模型識別率對比Fig.4 Comparison of recognition rate of each model

在-15～-10 dB信噪比條件下，利用各模型對測試集信號進行分類識別，預測信號類別與真實信號類別生成的混淆矩陣如圖5所示。BPSK，CW，LFM信號特征差異明顯，所有模型各信噪比條件下均能對其進行準確識別，其余4種雷達輻射源信號，不同的網絡模型有不同程度的混淆。對比來看，改進殘差網絡模型對ResNet18模型對NLFM信號的識別率低于其他4種模型，對BFSK，QFSK，QPSK信號的識別率均高于其他4種網絡模型，而且改進殘差網絡模型對各類輻射源信號的識別較為穩定，對NLFM信號識別率最低，為66.3%，略遜于ResNet18模型，該模型對BFSK信號的識別率最低，為73.7%，遠高于其他3種模型，AlexNet模型對QPSK信號的識別率不到50%；GoogLeNet模型對NLFM信號的識別率不到50%，對QPSK信號的識別率僅為55%；MobileNetV2模型對BFSK信號的識別率僅為50.67%。這說明改進后的殘差網絡模型在低信噪比條件下對“不易識別”的雷達信號依然具有較高且穩定的識別率。

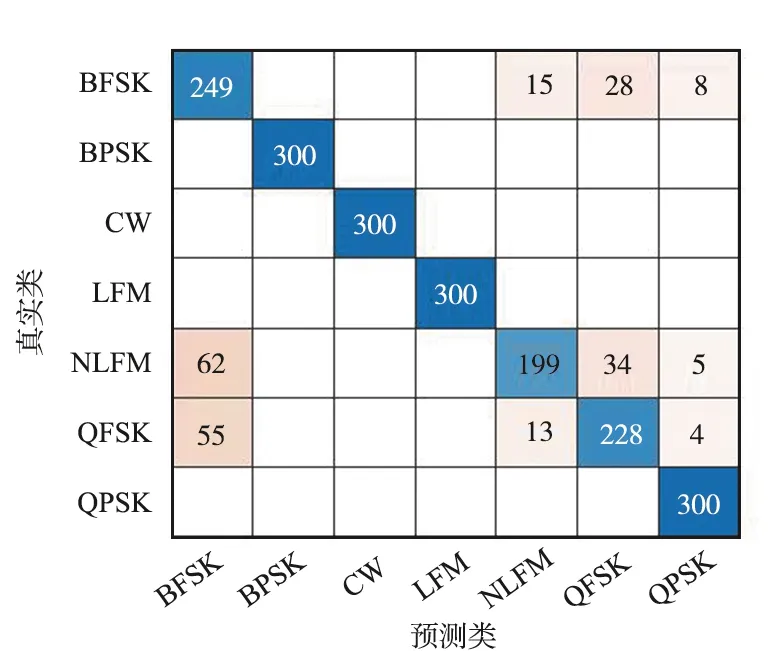
(a) 改進殘差網絡模型

(b) ResNet18模型

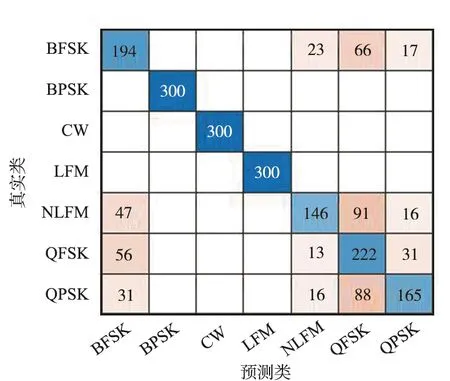
(c) GoogLeNet混淆矩陣

(d) MobileNetV2混淆矩陣

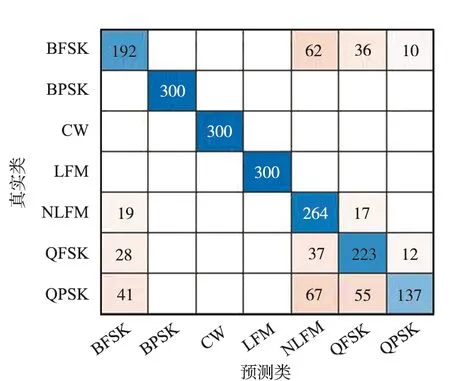
(e) AlexNet混淆矩陣圖5 各網絡模型混淆矩陣Fig.5 Confusion matrix of each network model

綜合以上實驗結果，可以驗證本文提出的改進殘差網絡模型的有效性。改進殘差網絡模型具有殘差網絡的結構優勢，能夠緩解梯度消失的現象，保證有效信息傳輸。因此，識別率和魯棒性均優于其他3種非殘差網絡模型。與殘差網絡ResNet18模型相比，在不同信噪比條件下的識別率和魯棒性方面互有優劣，綜合性能較為接近。但是，本文改進模型通過對模型體量和結構進行精簡優化，兼顧了模型性能和復雜度。因此，改進后模型復雜度和模型規模大大減少，相應的時效性也得到提高，便于工程上的設計和應用。

4 結束語

本文提出了一種基于改進殘差網絡的雷達輻射源識別方法，改進后的殘差網絡模型以殘差網絡為主體結構，同時借鑒了輕量化與“去網格效應”的設計思想，在保證模型性能的同時，降低了模型的復雜度。實驗結果證明，在綜合考慮識別率、魯棒性以及復雜度的情況下，本文改進后的模型性能優于其他文獻提出的網絡模型。同時，本文提出的模型以及設計方法可以為工程上的網絡模型設計和應用提供參考。