一種高誤碼率下QC-LDPC碼的快速識別算法
宋秉璽,李廣峰,楊 松,郭曉東
(1.河北省電磁頻譜認知與管控重點實驗室,河北 石家莊050081;2.中國人民解放軍91746部隊,北京100094)
0 引言
在非合作情況下,信道編碼參數是不能直接獲取的,需要分析識別信道編碼參數。QC-LDPC碼是一種具有準循環特性的LDPC碼,其校驗矩陣都是由單位陣的循環移位構成的[1-3]。QC-LDPC碼譯碼算法可采用并行結構,方便硬件實現,可以達到很高的吞吐率[4-5],因此在實際系統中被廣泛應用,所以針對QC-LDPC碼進行盲識別研究具有重大的科研意義,而LDPC碼的稀疏校驗矩陣重構是其識別的關鍵技術。文獻[6]介紹了LDPC碼在無誤碼下條件的校驗矩陣重構的基本方法。文獻[7]介紹了一種通過列相關關系剔除有誤碼碼字的方法,但二者都要求數據量很大,且誤碼率不能太高。文獻[8]相比文獻[7]實驗結果上略有提升,但需求數據量依然很大。本文提出了一種位置矩陣與循環位移值分步識別的方法,降低了高斯消元法的方程維度,該方法可以在低信噪比、高誤碼率的情況下仍保持良好的識別準確率[9-10]。
1 校驗矩陣稀疏化基本方法
在信道信噪比高的情況下,如圖1所示,針對無誤碼LDPC碼數據,可以通過高斯消元法,獲取LDPC碼的一組生成基,此生成基即為生成矩陣。生成矩陣和校驗矩陣之間為轉置關系,由此可以得到校驗矩陣。但此種方法得到的校驗矩陣并不是一個稀疏矩陣,不能用來譯碼,需要通過行變換,使其成為可用來譯碼的稀疏校驗矩陣[11-12]。

圖1 無誤碼校驗矩陣獲取流程圖Fig.1 Flowchart of obtaining check matrix
以IEEE802.16標準使用的QC-LDPC碼為例,給定LDPC(576,288),使用無誤碼數據高斯消元可得生成矩陣,如圖2(a)所示,由對應關系可得校驗矩陣如圖2(b)所示,之后通過行變換,稀疏化矩陣為圖2(c)所示。

(a) 生成矩陣
2 誤碼碼字識別
在信噪比低的情況下,解調碼流存在誤碼,無法通過碼字行之間的高斯消元法,直接獲得生成矩陣與校驗矩陣,需要剔除含誤碼碼元。可通過列之間的高斯消元法來判斷碼字中是否有誤碼。由于碼字M=[m,mG],校驗列是由信息列線性運算獲得的,做列高斯消元可以化簡為全0列,當數據存在少量誤碼時,由于誤碼影響,誤碼行信息位將化簡為全0,或者與誤碼行數值相等的列,化簡為基本為0列。此規律當誤碼較多時,由于誤碼之間的相互影響將不存在。以LDPC(576,288)碼加誤碼舉例,做列消元可以等價為數據轉置后做行消元,圖3中全0概率很高的行與列位置,即為誤碼行所在位置[13-14]。
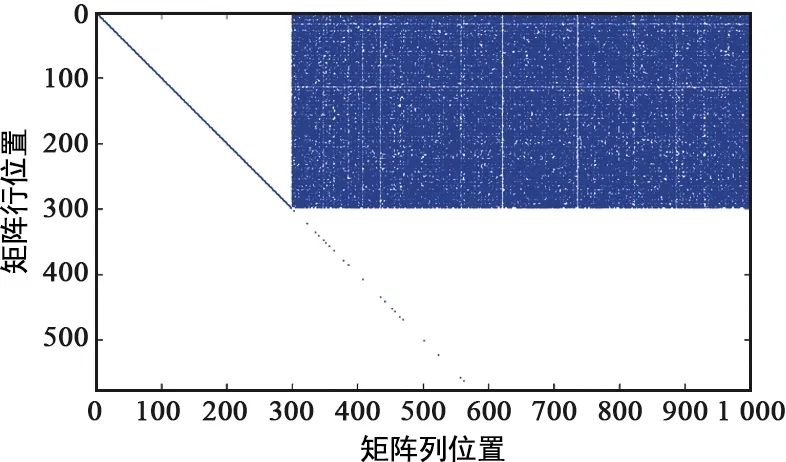
圖3 列高斯消元結果圖Fig.3 Gauss elimination result use of column
當誤碼率高時,單次列高斯消元法無法剔除所有誤碼行,需通過多次使用列高斯消元剔除誤碼數據,直至矩陣的秩等于信息位碼長(一般可以通過估計的碼速率計算)為止,進而通過校驗矩陣稀疏化基本原理,求取校驗矩陣。但此處理方式需要很大的數據量,并且誤碼率不可太高。通過實驗仿真發現當原碼矩陣的列中存在多個誤碼時,無法剔除誤碼行。
3 QC-LDPC校驗矩陣快速獲取方法
上文提到的校驗矩陣獲取方法是同時獲取二者,這需要巨大的數據量和復雜的高維向量運算,對于碼長較長LDPC碼校驗矩陣獲取不利。求解校驗矩陣所需的數據量與碼長N成N2比例關系,高斯消元所需的數據量與碼長N成N3比例關系。當碼字數據量不足,或者誤碼率過高的情況下,如何求解QC-LDPC校驗矩陣是本文研究重點。QC-LDPC是由位置基本矩陣和循環位移值來確定的[15]。本文通過先構造位置基本矩陣求得循環塊位置,再抽取碼元數據計算循環位移值,這樣通過分布方法獲得稀疏矩陣,其可以簡化數據運算,降低數據量的需求。
3.1 位置矩陣獲取方法
QC-LDPC碼是按循環位移單元進行編碼生成的,所以一個循環位移塊可以看為一個整體,可以通過碼元先構造位置獲取向量組,其保留了循環單元位置信息,丟掉循環位移值的細節信息,這樣做的好處是極大地縮小了碼長,使高斯消元方程維數降低,所需整體碼數量減少。假設循環塊大小為z,則數據維數為原數據碼長的1/z,所以所需數據量減少為原來的1/z2,計算量為1/z3,并且對誤碼容忍度更高。以LDPC(576,288)為例,其位置獲取向量組做高斯消元之后的結果如圖4所示,之后行之間做變化求得位置矩陣,如圖5所示。
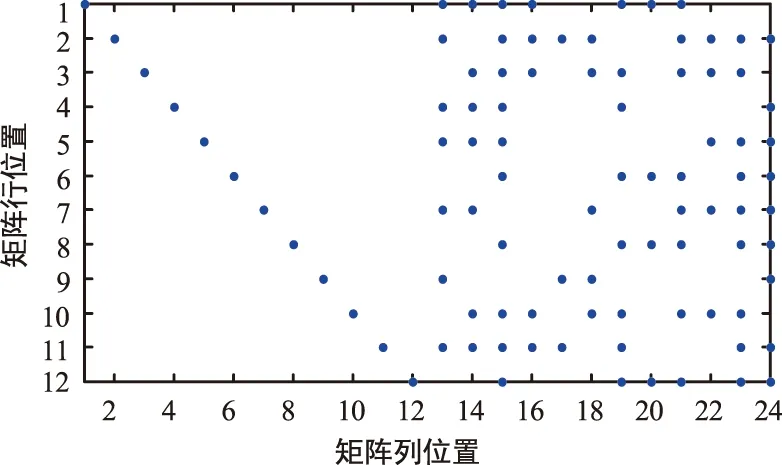
圖4 位置生成矩陣Fig.4 Position generation matrix

圖5 位置矩陣Fig.5 Position matrix
通過對比圖5與圖2(c)可知,位置矩陣的點出現的位置與實際校驗矩陣的循環校驗單元所在的分塊位置完全一致,證明此提取方法的正確性。求解過程中如若有誤碼行,用列高斯消元法剔除。
實際應用中z可能是未知的,需要通過把碼長N進行因子分解,窮舉所有因子,以是否可以得到位置矩陣為判斷依據,求得循環單元z。
3.2 循環位移值求解方法
在得到校驗位置矩陣后,需對每個位置的循環位移值求解。由于校驗關系只與每一行參與校驗的比特有關而與其他比特無關,所以按位置矩陣提供的信息,把相互校驗的循環位移塊提取出來,然后做高斯消元,進而得到循環位移值。依然以LDPC(576,288)碼為例,其位置矩陣第一行值為1的位置有[2,3,9,10,13,14],由z=24計算循環塊在原碼字所處列為[25~48,49~72,193~216,217~240,289~312,313~336],在原碼字中提取這144列,除去誤碼行,做高斯消元,解得矩陣如圖6所示。

圖6 相關循環塊-行高斯消元結果圖Fig.6 Correlation loop block-row Gaussian elimination result
提取矩陣最后24列,做轉置即為各個位置塊的循環校驗矩陣,如圖7所示。再把循環校驗矩陣放到[25~48,49~72,193~216,217~240,289~312,313~336]位置列上,其他位置為全0陣,即可得到QC-LDPC碼的稀疏校驗矩陣的前24行取值,如圖8所示。之后依次按位置矩陣的后續行,取實際數據列,做高斯消元,可以每次解得24行校驗矩陣,逐步獲得全部稀疏校驗矩陣。
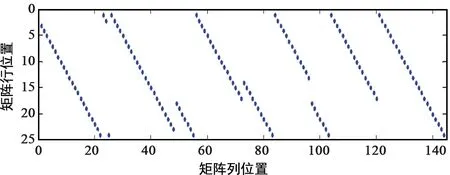
圖7 相關循環塊-循環位移值Fig.7 Correlation cyclic block-cyclic displacement value

圖8 校驗矩陣前24行取值圖Fig.8 Value of the first 24 rows of the check matrix
在獲得多行校驗行后,可預先憑借得到的部分校驗矩陣,對碼元進行譯碼,從而降低原數據誤碼率,有利于后續校驗行的獲取。
3.3 算法整體過程
通過上文的研究分析,對于誤碼下QC-LDPC校驗矩陣快速獲取方法,可以歸結為以下的整體算法步驟。
① 選幀長大于1的最小整數因子為循環位移塊長度;
② 通過原碼元數據獲取位置向量組,得到只含有位置信息的位置獲取數據;
③ 數據做列高斯消元,去除誤碼碼字;
④ 把只含位置信息的碼流,按做行高斯消元,得到位置生成矩陣;
⑤ 判斷矩陣的秩是否合理,或者得到的生成矩陣是否簡潔,如果是則轉入步驟⑥,否則選取下一個因子轉入步驟②;
⑥ 把位置信息生成矩陣轉化為位置矩陣;
⑦ 按位置信息,在原碼元數據中提取具有相關關系的循環塊數據所在列位置,生成新的只含有循環位置信息的碼流數據;
⑧ 數據做列高斯消元,去除誤碼碼字;
⑨ 用只含有循環位置信息的碼流數據,做行高斯消元,得到生成矩陣;
⑩ 由生成矩陣得到循環塊位移值,并按位置矩陣填入校驗矩陣所對應位置;
具體流程圖如圖9所示。
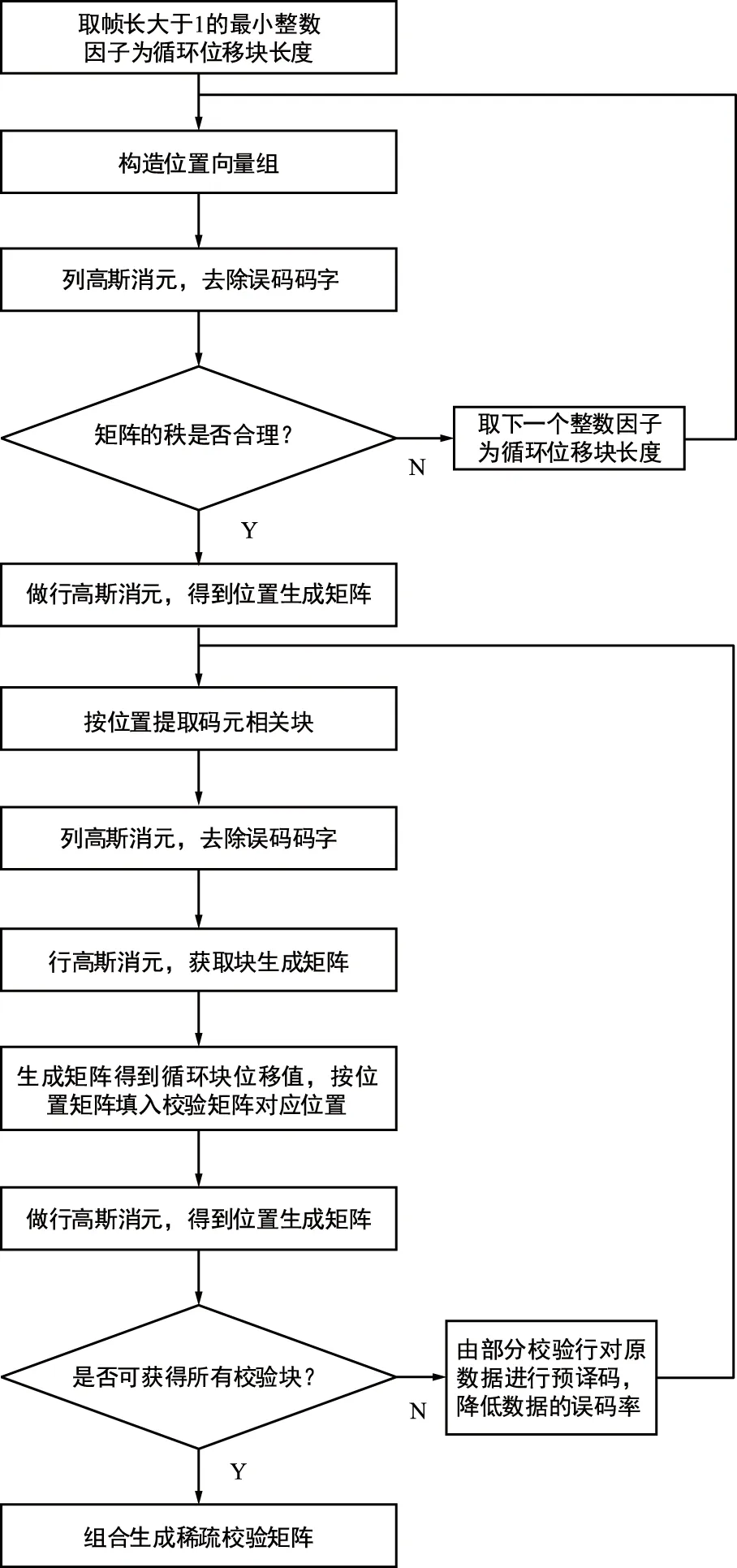
圖9 誤碼下QC-LDPC校驗矩陣快速獲取算法流程圖Fig.9 Flowchart of QC-LDPC check matrix fast acquisition algorithm under bit error
4 結論
本文研究了對未知協議下QC-LDPC碼稀疏矩陣分析方法,提出了位置矩陣與循環位移值分步識別的方法,降低了高斯消元法的方程維度,可以有效降低識別所需數據量與運算時間,并且支持在誤碼下進行分析識別。該方法尤其適用于碼長大的QC-LDPC碼識別,可極大地降低算法所需運算的時間。

