時間離散的時滯三維K-型競爭擴散系統的行波解
2023-01-03 07:48:08彭華勤朱慶
純粹數學與應用數學 2022年4期
彭華勤,朱慶
(廣西師范大學數學與統計學院,廣西 桂林 541004)
1 引言
根據物種的多樣性,種群之間的相互作用普遍存在,因此研究物種間的相互作用一直是生物數學中的一個重要課題.行波現象廣泛存在于各學科中,它能夠解釋自然界中的許多現象而備受學者們關注[1-3].時滯現象在日常生活中經常發生,在研究人口動力學,種群生態學,傳染病學等學科時通常需要考慮時滯所帶來的影響,對具有時滯反應擴散方程的行波解已經被廣泛地研究[4-7].對連續模型進行離散化是得到離散模型的一種方法,離散化后的模型通常具有非常豐富的動力學性質,并且在描述時空現象中也起到了十分重要的作用,因此對這類系統已有深入的研究,相關的理論研究包括行波解和漸近傳播速度[8-16].

2 一般理論
在本文中,將使用R3中的標準序,首先給出系統(3)的行波解的概念.


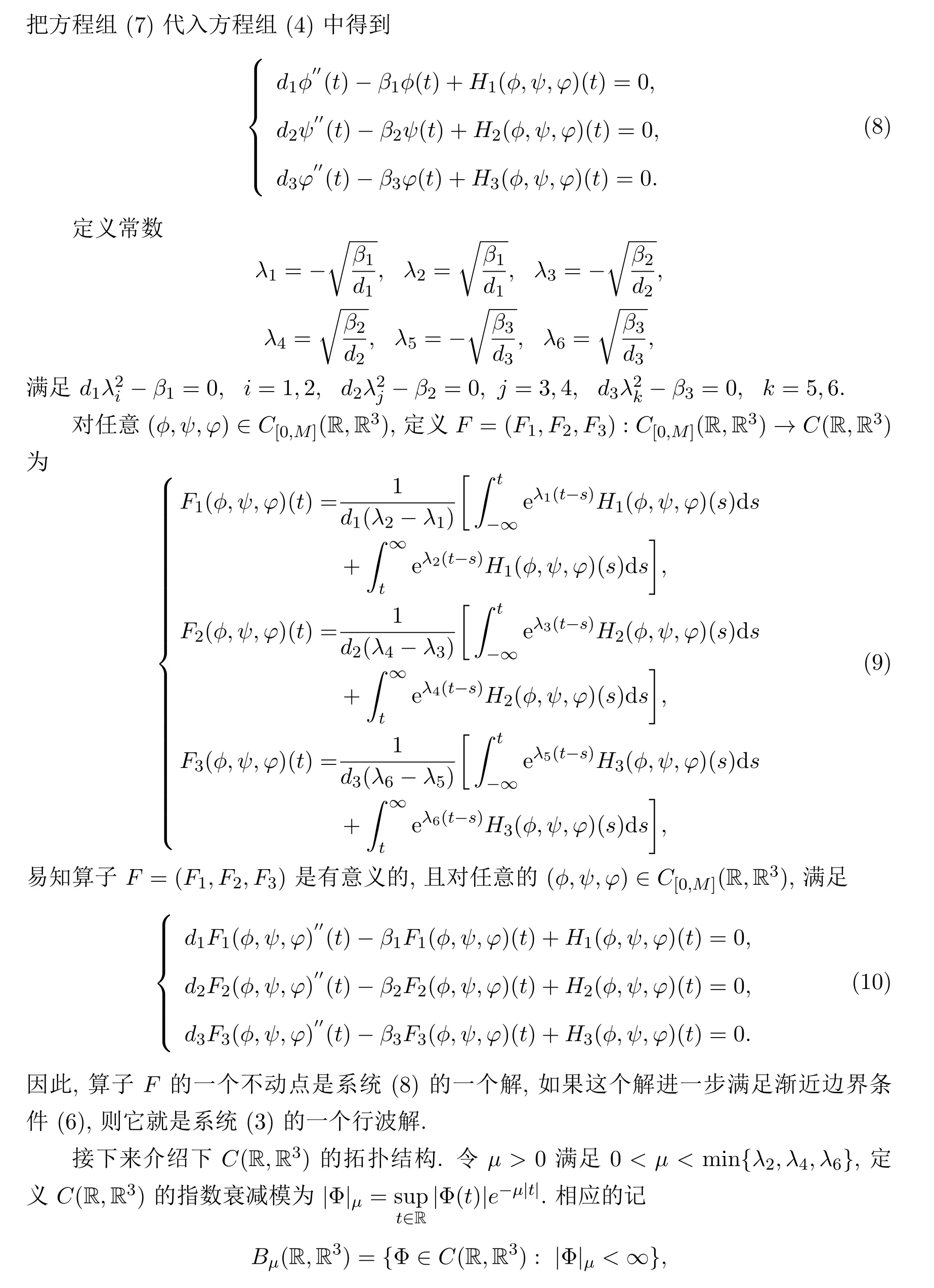

3 系統 (4)行波解的存在性



4 應用







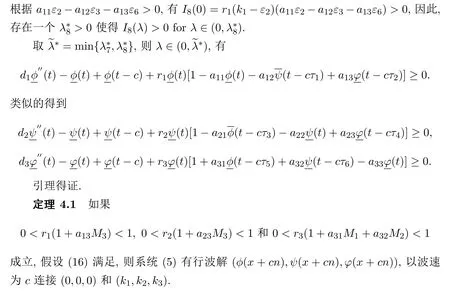
猜你喜歡
童話王國·奇妙邏輯推理(2024年5期)2024-06-19 16:03:38
英語世界(2023年10期)2023-11-17 09:18:18
中學生數理化·七年級數學人教版(2020年10期)2020-11-26 08:24:50
數學物理學報(2020年2期)2020-06-02 11:29:24
科學大眾(中學)(2019年3期)2019-05-17 10:04:30
汽車觀察(2018年10期)2018-11-06 07:05:26
光學精密工程(2016年6期)2016-11-07 09:07:19
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
少兒科學周刊·少年版(2015年1期)2015-07-07 17:15:12

