亞高斯隨機矩陣的稀疏恢復
宋儒瑛,鄭珂,關晉瑞
(太原師范學院數學系,山西 晉中 030619)
1 引言
壓縮感知是一種尋找欠定線性系統的稀疏解的技術.近些年來,該領域進行了大量的研究.Donoho和Cand`es及Tao[1-2]的開創性工作成功地解決了這些問題,即通過研究m×N測量矩陣A以及恢復算法,找到壓縮感知模型y=Ax的最稀疏解.選擇合適矩陣是利用了概率論的方法,得出結論:大多數隨機選擇的矩陣可以有效地重建稀疏向量.重建問題在于解決可計算的凸優化問題
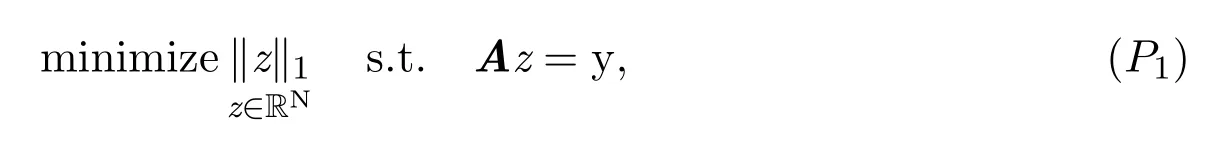
來取代NP-困難非凸優化問題

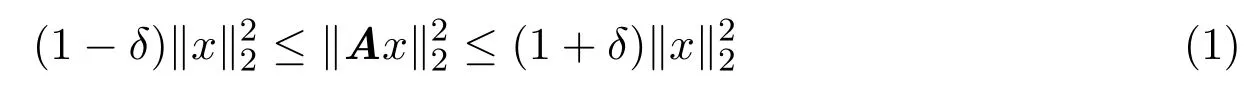
時具有第k階限制等距性質.其中滿足不等式(1)的最小常數用δk表示,并稱其為矩陣A的最小限制等距常數,詳見文獻[4].對于滿足集中不等式的隨機矩陣,由限制等距性質(1)以及測量值滿足m≥csln(eN/s)的條件下,推導出?1最小化稀疏恢復是可能的,文獻[5]有相關證明.當隨機矩陣是亞高斯隨機矩陣時,詳見文獻[6].
對于亞高斯隨機矩陣,經典的限制等距性質可以做出一些相應的修正.取限制等距性質中內范數為?2范數,外范數為文獻[7]中涉及到的外部范數,即

其中
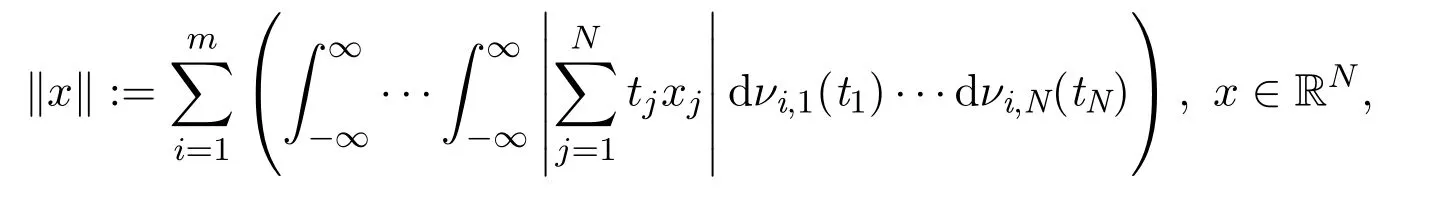
如果每個νi,j的第一個絕對矩是有限的,那么很容易驗證出現在文獻[8-10]中的這種表達式定義了RN上的范數.該外部范數依賴于概率分布構成了研究的新穎性.由此得到的修正限制等距性質如下:
一個項ai,j是根據中心概率測度νi,j分布的隨機矩陣A∈Rm×N,它的最小限制等距常數δ∈(0,1),使得

成立,其中k稀疏向量x∈RN.
本文在第一部分中介紹了相關的預備知識,第二部分建立了關于范數(2)的集中不等式,在第三部分中證明了修正了的限制等距常數是足夠小的,第四部分中證明了測量矩陣滿足修正限制等距性質(3),相對于歐幾里得范數而言,可以通過?1-最小化進行稀疏恢復.第五部分結合前面的結果得出主要定理.第六部分運用實驗驗證了定理結果的正確性.為了解釋的清楚,可以選擇只處理從完美測量中恢復精確稀疏向量的問題.
2 預備知識
首先從亞高斯隨機變量的定義以及它的等價性條件開始.


3 亞高斯尾衰減
4 修正限制等距性質



5 稀疏恢復


6 主要定理


7 實例驗證


圖1 不同稀疏度的信號重建
根據圖1可知,隨著測量值的不斷增大,信號成功恢復的概率也不斷增大,那么根據常數C2的大小可知,本文所證明的定理中測量值的條件足以使得信號進行稀疏恢復,定理得以驗證.
8 結束語
本文通過應用依賴于概率分布的范數,證明了一個具有獨立亞高斯隨機系數的m×N欠定線性方程組滿足限制等距性質時,在最優條件m≥csln(eN/s)下,系統的s稀疏解可以通過?1最小化得到.在Simon Foucart,Ming-Jun Lai等人對于預高斯隨機矩陣稀疏恢復的基礎上,對亞高斯隨機矩陣稀疏恢復進行了證明,并且將文獻[11]限制等距性質中?2范數用依賴于概率分布的范數取代,得出了新的結果.

