有軌電車轉向架軸橋裝置振動特性分析

□ 任春吉 □ 陸亞龍

中鐵二局集團新運工程有限公司 成都 610036

1 研究背景

有軌電車轉向架系統內部結構較復雜,考慮到低地板結構,動力轉向架通常采用獨立旋轉車輪耦合驅動結構,提高轉向架整體導向性[1]。有軌電車內部動力轉向架傳遞振動并搭接傳動系統與車體的部件為動力軸橋,通常布置在轉向架構架側面,多采用架懸方式,實現車輪的獨立轉動[2]。動力傳遞路徑為電機、聯軸器、輸入齒輪軸、輸出齒輪、輸出聯軸節、車輪[3]。為了提高電車性能和舒適度,有軌電車逐漸出現低地板化的趨勢,現如今我國常見的有軌電車地板面距離地面一般不超過400 mm[4]。

軌道隨機不平順屬于軌道典型的不確定性激勵,具有較悠久的研究歷史。羅林[5]在研究軌道不平順測量時,提出了慣性基準法并進行大量實測,列舉了平穩軌道下的功率譜密度樣本。陳果等[6-7]在模擬軌道不平順時域樣本時,采用頻譜功率譜的等效算法求出了不平順功率譜隨機相位,提升了時域樣本精度,之后基于我國高速鐵路無砟軌道總結了軌道不平順平均譜擬合系數。

國外學者對軌道不平順功率譜函數也進行了針對性研究。Ontes等[8]提出二次濾波法來實現軌道不平順的時頻轉換,設計出合理濾波器,得到理想狀態下的不平順時域樣本。Garg等[9]將線路不平順擬合成以截斷頻率表示的偶次函數,并歸納軌道表面粗糙度參數列為美國標準軌道譜參數。Sadeghi等[10]從波長的角度分析了振幅對平順性的影響,研究表明,軌道不平順波長小于0.75 m時,鐵路線路的乘坐舒適性顯著降低,為軌道不平順幅值研究提供參考依據。

關于轉向架外部激勵的研究內容雖然悠久,但具有一定單一性,鮮有綜合考慮輪軌間激勵、軌道激勵等外部激勵,以及齒輪系統內部激勵對動力轉向架軸橋振動特性的影響。筆者以某型號低地板有軌電車動力轉向架軸橋為研究對象,開展針對軸橋裝置外部軌道激勵及齒輪系統內部激勵的分析,在此基礎上進行動力轉向架軸橋裝置振動特性響應的相關研究[11-12]。

2 動力轉向架結構

動力轉向架結構如圖1所示,某型號低地板有軌電車將牽引電機放置在轉向架一側,有軌電車一節車體配置有兩部分軸橋裝置,其中電機牽引實現車輪轉動的軸橋裝置稱為動力轉向架軸橋。軸橋裝置的傳動系統置于動力軸橋殼體內,由多級平行軸傳動組成,采用的齒輪模數、材料均相同。由于車輪通過軸橋直接連接,轉向架高度能夠保證與地面的距離不超過400 mm,車輪部位高度基本與軸橋裝置齊平,實現車體內部低地板占有量達到100%。

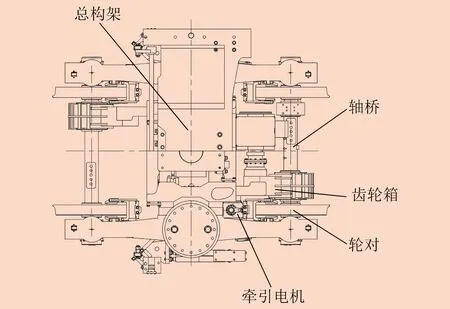
圖1 動力轉向架結構

3 軌道高低不平順激勵分析

3.1 軌道激勵

軌道激勵是造成低地板有軌電車振動的重要來源之一,軌道激勵通過軌道依次傳遞至車輪、動力軸橋、轉向架,以及車體。其中非確定性激勵主要指軌道的幾何隨機不平順,幾乎會一直伴隨著有軌電車的行進而存在。這種振動由軸橋裝置傳遞至轉向架整體,長期會造成車體振動加劇,影響乘客乘坐舒適度和物品運送的平穩性,嚴重時會造成軌道線路的變形積累,造成軌道幾何形狀的惡化。

軌道高低不平順如圖2所示。左右軌道頂面法向偏移引起軌道中心線法向偏移,使得有軌電車行進過程中輪軌間垂向作用力激增,是造成行駛過程中車體顛簸的主要原因。

圖2 軌道高低不平順

3.2 軌道高低不平順時域模擬

通過長期試驗,以及與國外軌道譜的對比,我國一般干線鐵路線路幾何狀態即常態,軌道的不平順功率譜密度函數S(f)可表示為:

(1)

式中:f為空間維度頻率;A、B、C、D、E、F、G為功率譜密度函數的特征參數,取值見表1。

表1 軌道功率譜密度函數特征參數

設功率譜密度函數S(f)在離散點的功率譜密度函數表示為Sx(f),那么功率譜密度函數與離散點頻譜關系表示為:

(2)

式中:X(f)為離散點的時間序列頻譜;X*(f)為常態時間序列頻譜;Nc為空間計算頻率;xs為第s個采樣頻率;xj為第j個采樣頻率。

在進行時頻轉換之前,先將功率譜密度函數轉換為雙邊譜密度函數Sk(f),并將時間序列用[Xt]表示。設采樣總時間為Tz,采樣周期ΔT,則采樣點數Nr為:

Nr=Tz/ΔT

(3)

離散點的時間序列頻譜的模值|X(f)|為:

(4)

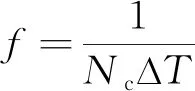
(5)

式中:Δf為空間維度頻率的分量。

隨機性是時間序列頻譜相位具備的特征,這里設相位為ξn,考慮到實序列的快速傅里葉變換為復序列,則ξn為復數,于是有:

ξn=cosφn+isinφn=exp(iφn)

(6)

φn為復數域中的旋轉因子,在0～2π的范圍內均勻分布。

時間序列[Xt]的實部在Nc/2處滿足偶對稱,在計算過程中只考慮離散點時間序列在0～2π范圍內的頻譜,結合式(4)和式(6),可以得到:

(7)

計算過程中,只需將式(7)在MATLAB軟件中進行傅里葉逆變換,得到軌道不平順時域模擬樣本曲線,可將高低不平順的時域激勵信號轉化為軌道與車輪側面接觸區域處的法向作用力F(f),表達式為:

F(f)=[Xω(f)/G]3/2

(8)

Xω(f)為經過傅里葉逆變換后的輪軌高低不平順時域激勵信號,即兩車輪與軌道之間的彈性變形量。G為輪軌赫茲非線性彈性接觸常數,G的數值與車輪踏面的結構形狀有關。當車輪為傾斜錐型踏面時,G為:

G=4.57×10-8R-0.149

(9)

式中:R為車輪的實際滾動圓半徑。

3.3 軌道高低不平順模擬結果

基于上述方法,已知型號的有軌電車最高行駛車速為80 km/h,其它工況信息為:額定輸入轉速為2 600 r/min,負載轉矩為440 N·m,額定功率為120 kW,通過表1選取左、右軌道的特征參數并代入到式(1)中,計算得到有軌電車勻速運行10 s的高低不平順位移響應,如圖3所示。

圖3 高低不平順位移模擬

由圖3可以看出,軌道沿高低方向的波動幅值在-2～2 mm范圍內變化,不平順程度具有一定的波動性,但波動程度相對穩定。

有軌電車在行駛過程中轉向架車輪部位會受到隨機的法向力,根據模擬的時域激勵信號,由式(8)得出有軌電車行駛過程中輪軌受到的法向力,如圖4所示。

圖4 輪軌法向力

由圖4可以看出,兩側車輪在運行時間內受到的輪軌法向力波動范圍集中在-40～40 kN內,沒有出現較大偏差,幾何狀態較好。

輪軌法向力能影響動力軸橋的垂向振動,將左、右兩側車輪的輪軌法向力進行平順優化處理,消除波動較大數值,再經由傅里葉變化得到輪軌法向力頻譜,如圖5所示。

圖5 輪軌法向力頻譜

由圖5可以看出,輪軌接觸運動時,法向力在中低頻附近約323 Hz出現峰值,且在其倍頻處也能看到較小但有明顯的幅值,證明軌道不平順激勵中垂向不平順在中低頻段會對輪軌接觸產生較大的影響,將出現峰值處的頻率視為輪軌間的振動頻率。

4 動力轉向架軸橋振動響應分析

基于ANSYS軟件編寫APDL加載程序,將齒輪系統動態嚙合力施加在齒輪嚙合線附近的節點上。確定約束及載荷邊界條件后,采用模態疊加法計算軸橋裝置振動響應,建立動力轉向架軸橋有限元分析模型如圖6所示。

圖6 動力轉向架軸橋有限元分析模型

為驗證內、外部激勵下的軸橋裝置振動特性,在動態嚙合力的基礎上考慮軌道不平順激勵,分析嚙合力對動力轉向架軸橋振動特性的影響程度,并在計算完成后選取動力轉向架軸橋外部殼體上六個節點作為響應結果評價點,如圖7所示。

圖7 動力轉向架軸橋振動響應評價點

各節點無外部激勵時計算結果整理見表2。

表2 無外部激勵時振動加速度均方根值

同理給出考慮外部激勵的結果,整理見表3。

表3 有外部激勵時振動加速度均方根值

從表2、表3中數值變化可以看出,受到外部激勵影響時,各評價點的振動加速度均方根值均有所增大,且左右兩側輸出端即節點3和節點4的增幅較明顯,主要原因是外部激勵作用位置集中在輸出端,而輸出端受輪軌法向力作用的Z方向的加速度響應增幅最明顯。

為了更好地研究觀察外部激勵影響下評價點振動響應的變化,分別給出不同激勵條件下輸出端節點4法向振動加速度結果的時域、頻域圖對比,如圖8、圖9所示。

圖8 無外部激勵時節點4 Z向振動響應時頻曲線

圖9 有外部激勵時節點4 Z向振動響應時頻曲線

由圖8、圖9可以看出,系統振動規律基本保持一致,當受到外部輪軌激勵影響時,低頻附近變化不明顯,而在300～500 Hz的中低頻段附近頻率更加豐富,且323 Hz附近呈現明顯幅值,反映了輪軌間赫茲彈性接觸的頻率振動,以及輪對在外部激勵作用下的整體彈性振動。

5 結束語

筆者通過對軌道功率譜密度函數的推導,得到軌道離散點不平順時域序列頻譜,計算得出在最高行駛速度下的軌道法向位移并轉換為輪軌法向力。結果表明軌道高低不平順產生的輪軌法向力在中低頻約323 Hz附近出現峰值。考慮外部激勵時,轉向架軸橋裝置輸出端處節點3和節點4的振動響應明顯增大,在中低頻約323 Hz附近法向振動加速度幅值更加豐富,在軌道高低不平順的作用下出現中低頻車輪與軌道的耦合振動。