傷員轉運機器人機械臂運動學與動力學分析
□ 王天賜 □ 郭繼錄 □ 李艷杰
沈陽理工大學 機械工程學院 沈陽 110001
1 傷員轉運機器人簡介
傷員轉運機器人的核心部件包括移動平臺、腰部機構,以及雙機械臂。移動平臺負責移動傷員至指定位置,腰部機構搭載雙機械臂,雙機械臂執行抱起傷員動作以完成救援任務。可見機械臂是傷員轉運機器人功能實現的核心部件,機械臂運動學與動力學研究能夠解算其一系列動作過程中各個關節所需要的驅動力矩。
傷員轉運機器人搭載的雙臂是對稱的,單臂包含六個轉動關節,末端執行器類似擔架結構,起承重和保護作用。機械臂完全伸展長度可達1 500 mm,質量為68 kg,可承受40 kg負載。筆者選取雙機械臂中的左臂進行運動學與動力學相關研究,其三維結構簡圖如圖1所示。

圖1 機械臂三維結構簡圖
2 機械臂運動學分析
2.1 機械臂運動學方程
傷員轉運機器人機械臂三維結構模型,采用改進D-H(Denavit-Hartenberg)法建立連桿坐標系,基坐標系建立在與雙機械臂連接的腰部中心處,改進D-H法連桿坐標系如圖2所示。獲得的改進D-H參數表見表1。

圖2 改進D-H法連桿坐標系
圖2中,xi、zi分別為連桿i坐標系的X軸、Z軸,下角標為0表示基坐標系。

表1 改進D-H參數表
表1中,a0為634.36 mm,a1為196.72 mm,a2、a3、a4、a5為0,d1為329.02 mm,d2為40 mm,d3為407 mm,d5為508 mm,α0為π,α1、α2、α3、α4、α5為π/2,θ1、θ2、θ3為π/2,θ4、θ5為π。
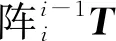
(1)
(2)
式中:(nx,ny,nz)為法向向量;(ox,oy,oz)為方位向量;(ax,ay,az)為接近向量;(px,py,pz)為機械臂的末端執行器中心在基坐標的位置向量。
2.2 機械臂運動學仿真
運用MATLAB軟件機器人工具箱來研究傷員轉運機器人機械臂的運動特性,對其進行運動學仿真分析。根據表1的具體參數建立機械臂的仿真模型,如圖3所示。

圖3 機械臂仿真模型
得到機械臂改進D-H模型,該模型是進行機械臂運動學、動力學分析的基礎。利用MATLAB軟件機器人工具箱在該模型基礎上計算機械臂運動學的正解與逆解,通過正逆解對機械臂各個關節進行軌跡規劃,方便后續動力學分析。
3 機械臂動力學分析
3.1 動力學建模方法概述
傷員轉運機器人機械臂動力學問題,其實就是研究各個關節角度、角速度、角加速度及其驅動力矩之間的關系。建立傷員轉運機器人機械臂精準的動力學模型,為機械臂動力控制奠定基礎,使機械臂實時力控制成為可能。
目前有很多機器人動力學建模方法,其中以拉格朗日法和牛頓-歐拉法應用最為廣泛。拉格朗日法的優點是從整個系統的能量角度出發,動力學方程簡潔,并且可有效避免方程中內力項的出現,計算效率高,但是在其建模過程中動能及勢能的推導較為復雜,廣義坐標的選取也存在一定的難度。牛頓-歐拉法的本質是基于矢量力學的系統動力學建模方法。其通過隔離系統的每個單元,利用牛頓第二定律及質心動量矩定理來推導單元質心平動方程,并根據歐拉原理來推導質心轉動方程,獲取整個系統每個單元的動力學方程;然后再依照各個單元間約束關系獲得整個系統動力學方程。牛頓-歐拉方程的形式直觀,且物理意義十分明確,推導得到的動力學方程也容易進行變換。所以筆者利用牛頓-歐拉法為傷員轉運機器人建立動力學模型。
3.2 機械臂動力學建模
將傷員轉運機器人機械臂各個桿件的慣性張量、連桿質量、質心矢量、關節角度、關節角速度及關節角加速度等參數代入牛頓-歐拉動力學方程,便可計算出對應的關節力矩。
各連桿質量中,m1為36.65 kg,m2為7.92 kg,m3為8.53 kg,m4為6.73 kg,m5為6.69 kg,m6為1.76 kg。
各質心矢徑為:
各慣性張量為:
4 基于MATLAB的機械臂動力學仿真
對準備抱起傷員的機械臂進行五次多項式運動規劃,在MATLAB軟件中對機械臂的動力學模型進行仿真。根據傷員轉運機器人機械臂的關節角度、關節角速度及關節角加速度等運動狀態,可以通過計算得到關節驅動力矩,動力學仿真結果如圖5所示。
從圖4中可以看出,在準備抱起傷員過程中,機械臂運動規劃速度與加速度都為連續且平滑曲線,且開始運動與結束運動速度及加速度都為零,保證了關節運動平穩。結合機械臂力矩曲線看出,由于在抱起傷員過程中關節1與關節4為主要受力點,因此,除了關節1跟關節4在運動過程中始終受力,其余關節力矩都趨向于零。這是因為從零加速至最大速度所需力矩最大,達到最大速度后所需力矩逐漸減小,最后遞減為零。結合角速度和角加速度來看,關節由靜止到運動、再由運動到靜止的過程中,力矩變化符合客觀事實,且符合受力要求,完全能夠滿足抱起傷員的需求。

圖4 動力學仿真結果
5 結束語
利用改進D-H法、牛頓-歐拉法對傷員轉運機器人機械臂,進行了運動學、動力學的分析,驗證了所建立的動力學方程的正確性,同時通過仿真過程輸出的力矩曲線得到機械臂各關節的受力情況,為后續的真機試驗提供了保障。

