基于聯邦自適應濾波的分布式傳遞對準方法

朱 敏，馬 振，王俊瑋，陳熙源

(東南大學儀器科學與工程學院， 南京 210096)

0 引言

分布式位姿測量系統可為高分辨率航空對地觀測系統多元載荷提供分布式高精度運動信息。但觀測平臺在飛行過程中受到載荷和湍流的影響，機翼發生撓曲變形和震顫，降低了主子節點之間傳遞對準的精度[1-2]。因此，提高分布式傳遞對準的精度成為航空對地觀測系統高分辨率成像的關鍵。

傳統的不考慮主子節點動態變形的傳遞對準誤差模型以及不考慮噪聲的時變特性和主子節點間信息融合的分布式卡爾曼濾波算法用于分布式傳遞對準時難以提供高精度信息。傳統傳遞對準誤差模型將機翼視為剛體，忽略了主子節點之間的動態變形，難以實現高精度測量。文獻[3-4]使用二階Markov模擬動態彎曲變形角，并將相關彎曲變形角和角速率加入狀態變量，但其模型中將動態杠桿臂視為常數，并不符合實際變形。文獻[5]建立了變形角和動態桿臂之間的模型，對主子節點之間的速度關系進行包括耦合關系在內的詳細分析。但在機載分布式傳遞對準過程中，機翼變形會增加桿臂的估計誤差，姿態以及角速度匹配方法可避免該誤差[6]。所以，主子節點之間角速度耦合關系，即機翼撓曲變形引起的角速度同子節點角速度方向不同而存在的耦合角也需要考慮。因此，在傳遞對準誤差模型建立時考慮了機翼的撓曲變形角、耦合角、主子節點的動態桿臂誤差。但在實際的工程應用中，盡管使用了較為精確的模型，復雜飛行環境的干擾仍會導致卡爾曼濾波精度下降，甚至濾波發散，自適應濾波方法成為研究重點[7-9]。文獻[10]提出了基于新息極大似然估計準則的自適應卡爾曼濾波器,實時估計出系統過程噪聲矩陣Q和量測噪聲矩陣R，可以較好估計出失準角，但每一次均要進行Q和R的估計，大的計算量會導致實時性降低。因此，考慮到傳遞對準的精度和時間，采用只對R進行不斷估計的方法，但狀態估計誤差會影響該濾波算法的穩定性。基于殘差的卡方檢驗[11]可有效解決該問題。因此，本文引入R更新和基于卡方檢驗的協方差矩陣P更新的卡爾曼濾波算法進行單點傳遞對準。但單一的自適應卡爾曼濾波用于分布式傳遞對準時抗擾動性能較差，可將不同的子濾波器進行信息融合以達到更好的效果[12]。在多節點信息融合算法中，聯邦濾波因其較好的容錯性而被廣泛應用，其通過實時確定信息權重系數的方式對聯邦濾波器進行了改進[13-14]。因此，本文結合分布式傳遞對準的背景和復雜飛行環境，以提高傳遞對準的精度和穩定性、縮短傳遞對準的時間為目標，提出了新型聯邦自適應濾波算法用于分布式傳遞對準，子濾波器采用基于R和P自適應更新的卡爾曼濾波(Adaptive Kalman Filter，AKF)并結合27維傳遞對準模型進行單點傳遞對準，主濾波器采用基于誤差協方差矩陣的范數的原則對多個子濾波器進行信息融合。

1 新型聯邦自適應濾波算法

1.1 分布式位姿測量系統

分布式位姿測量系統包括一個高精度的主IMU和多個子IMU，示意圖如圖1所示。由于飛機的機翼部分可承受質量有一定限制，所以機翼上安裝的多個子IMU為低精度。各個子節點處高精度運動信息的獲取需利用主IMU測得的高精度運動信息對分布于機翼的多個子IMU進行分布式傳遞對準濾波估計[15]。分布式傳遞對準精度取決于傳遞對準模型和分布式傳遞對準濾波方法。

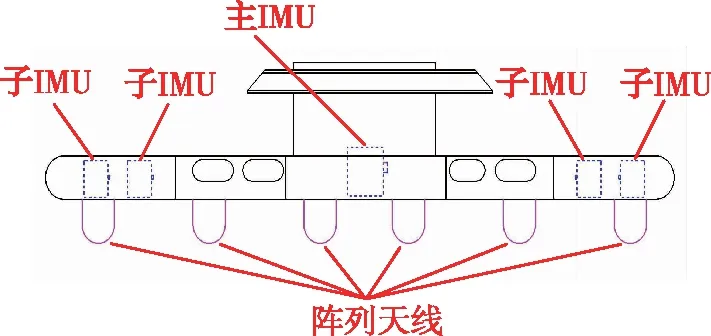
圖1 分布式位姿測量系統示意圖Fig.1 Schematic diagram of distributed position and orientation system

本文采用27維狀態量的傳遞對準模型，將機翼的撓曲變形角、耦合角、主子節點的動態桿臂誤差均進行考慮，模型[16]如下：

狀態方程中狀態變量為

(1)

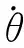
狀態方程中狀態轉移矩陣為

(2)

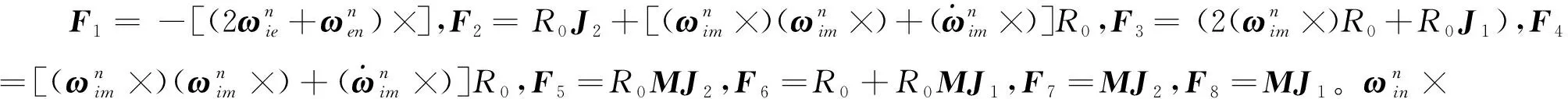
量測方程中量測量包括主子節點之間的姿態差Ya、速度差Yv和角速度差Yω

(3)

量測方程中量測矩陣為

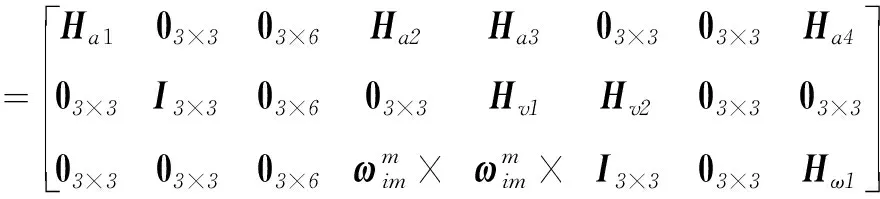
(4)

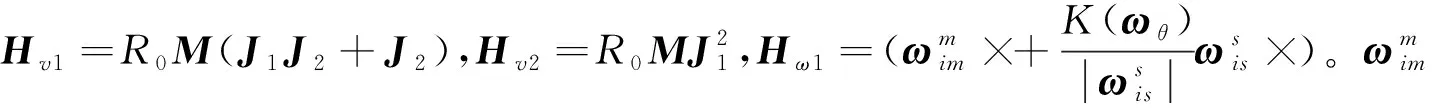
(5)

(6)

傳遞對準過程中不確定的模型以及時變的飛行環境噪聲等會帶來誤差。不考慮噪聲時變特性和主子節點信息融合的分布式卡爾曼濾波算法用于分布式傳遞對準時難以提供高精度信息。為了保證傳遞對準精度和穩定性，將新型聯邦自適應濾波算法用于分布式傳遞對準。子濾波器中使用基于R和P自適應更新的卡爾曼濾波算法，主濾波器基于誤差協方差矩陣進行信息融合。

1.2 自適應卡爾曼濾波算法

傳遞對準時系統模型會產生不可預知的變化，需不斷地估計Q和R來提高精度，但其存在著計算量大和自適應性差的問題。每一次濾波均要進行Q和R的估計，計算量大，實時性降低，并且隨著濾波遞推次數的增加,分配權重不斷減小，濾波自適應性降低[14]。為保證濾波精度和速度，采用基于R和P自適應更新的卡爾曼濾波算法。

針對實時性問題，在Sage-Husa自適應卡爾曼濾波的基礎上選擇只進行量測噪聲R更新的卡爾曼濾波算法。傳遞對準中主慣導采用高精度的IMU，同時還有相應的輔助導航設備以修正主慣導誤差，常認為主慣導輸出信息的精度較高并且較穩定。但是由于在實際傳遞對準中，受機翼撓曲變形和振顫的影響，機體運動速度、姿態以及角速度會發生變化，且變化較為復雜，雖在傳遞對準誤差建模中已針對機翼撓曲變形進行建模，但其并未完全消除機翼變形帶來的影響。相對于量測噪聲而言，系統過程噪聲受子慣導慣性器件誤差的影響較小。因此，為減少濾波器的計算量并增加其穩定性，本文采用只進行量測噪聲R更新的卡爾曼濾波算法，將量測噪聲R不斷估計并傳入，進行濾波增益的更新，從而達到更精確的狀態估計，具體算法流程如圖2所示。

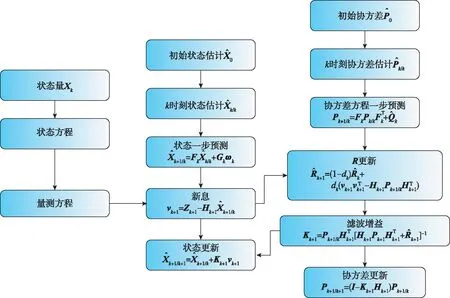
圖2 R更新的卡爾曼濾波算法Fig.2 Kalman filtering algorithm based on R-update

R更新方程中自適應系數dk和遺忘因子[14]關系如下

dk=(1-a)/(1-ak)

(7)

其中，遺忘因子a的取值范圍為0.95～0.99。

針對濾波的自適應問題，上述只進行R更新的卡爾曼濾波算法，在R更新方程中遞推次數到一定值后，自適應系數收斂為常數，歷史和新近的觀測信息對濾波的影響保持固定比例，歷史觀測信息對濾波影響較大，濾波的自適應性較差。所以，濾波過程中針對濾波遞推次數進行相應調整，每次濾波結束后判斷自適應是否為常數，若為常數，將濾波次數k從0開始計數，重新進行自適應調整，繼續執行圖2所示濾波過程。

然而，系統模型的不確定性會降低基于R自適應更新的卡爾曼濾波器的性能，只進行R更新的卡爾曼濾波算法易受到狀態估計誤差的影響，計算穩定性相對較差。為克服該問題，本文引入卡方檢驗以及自適應因子[17]。通過基于殘差序列的卡方檢驗評估傳遞對準模型的濾波穩定性，并采用自適應因子動態調整狀態估計誤差的均方誤差陣，具體如下：

通過卡方檢驗驗證濾波器是否平穩，當檢測到濾波不是最優時，P陣進行自適應更新，引入自適應因子調整狀態協方差矩陣并考慮對稱性，P的表達式更新為式(8)

(8)

其中，Sk為自適應因子。

當濾波最優時，殘差序列rk有下列屬性

(9)

其中，γk服從可觀測狀態變量的數量為m自由度的卡方分布。

式(9)中，令

(10)

(11)

(12)

根據式(9)可知，濾波最優時殘差序列的每一個分量滿足下列方程

γi(k)=[ri(k)]2/(aii(k)+bii(k))～χ(1)

(13)

其中，aii(k)為矩陣Ak的第i個對角線元素；bii(k) 為矩陣Bk第i個對角線元素。

對Ak進行分解可得到Ak和Jk的關系

(14)

其中，Jii(k)為矩陣Jk的第i個對角線元素。

結合式(13)和式(14)，自適應因子滿足下列方程

(15)

其中，εi為卡方檢驗的閾值。

檢測到濾波異常時，為使濾波正常，自適應因子公式如下

Si=

(16)

自適應因子矩陣中只有可觀測狀態量可以自適應計算，其余不可觀測的值均取為1。因此，可觀測狀態量的自適應因子取值如式(16)，不可觀測狀態量取值為1。

自適應因子矩陣表達式如下

Sk=diag(s1,s2,s3,…,sn)

(17)

綜上所述，基于R和P自適應更新的卡爾曼濾波算法整體流程如圖3所示。

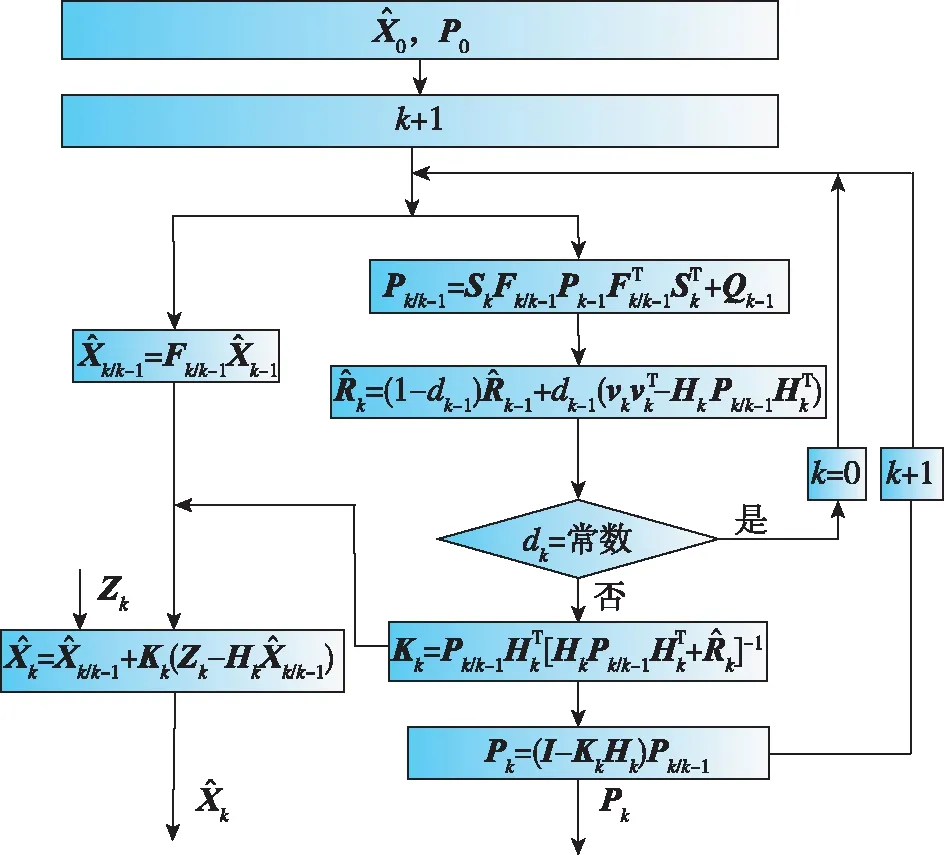
圖3 自適應卡爾曼濾波算法Fig.3 Adaptive Kalman filtering algorithm

1.3 基于誤差協方差矩陣的信息融合算法

為提高分布式傳遞對準精度和穩定性，采用基于誤差協方差矩陣的信息融合算法。結合子濾波器中的自適應卡爾曼濾波算法，以3個子IMU為例的新型聯邦自適應濾波算法的濾波結構如圖4所示。

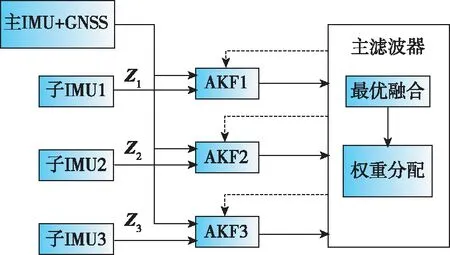
圖4 新型聯邦自適應濾波算法Fig.4 Novel federated adaptive filtering algorithm

子濾波器中分別進行基于R和P自適應更新的卡爾曼濾波算法的傳遞對準后，在主濾波器中通過信息融合進行全局最優估計，然后將計算出的協方差陣乘以信息分配因子系數,反饋給各個子濾波器進行權重的分配。信息分配因子αj為權重分配提供基準，其可通過誤差協方差矩陣P的范數被確定。子濾波器的濾波效果表達式如下

(18)

其中，j=1,2,3代表濾波器的序號。

信息權重因子αj的表達式如下

(19)

信息融合原則為

(20)

信息權重分配原則為

(21)

2 實驗結果及分析

2.1 半物理仿真實驗

為了驗證基于27維傳遞對準模型的新型聯邦自適應濾波算法的有效性，本文采用基于實際飛行數據的半物理仿真方法，使用Y12型飛機進行約200min、6000m高的飛行實驗，并記錄飛行數據。其飛行軌跡如圖5所示。

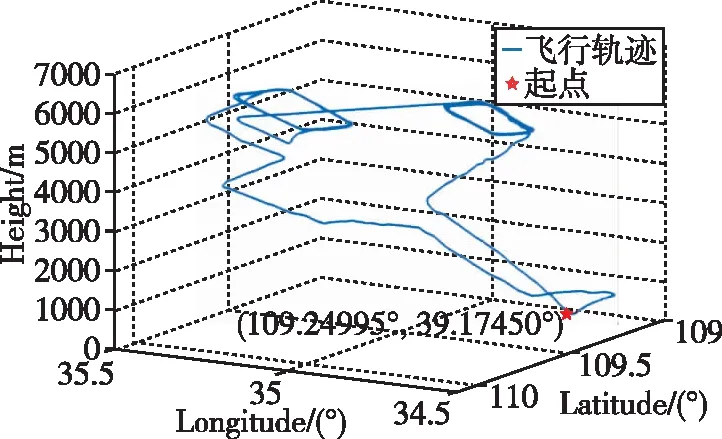
圖5 飛行軌跡Fig.5 Flight trajectory

實驗所使用的仿真數據基于上述實際飛行軌跡生成。其中主IMU數據采用本次飛行實驗數據，3個子IMU數據將飛行實驗中主IMU數據進行轉換，再疊加設定的子 IMU的誤差。參數設置如表1所示。

表1 子IMU參數設置

2.2 結果及分析

3個子IMU分別采用傳統卡爾曼濾波算法、聯邦自適應濾波算法、新型聯邦自適應濾波算法三種算法進行分布式傳遞對準,以證明聯邦自適應濾波算法以及自適應卡爾曼濾波算法的有效性，最終證明本文提出的新型聯邦自適應濾波算法的有效性。三種濾波算法均采用27維傳遞對準模型，選用桿臂誤差和姿態誤差作為評估對象。傳統卡爾曼濾波算法和聯邦自適應濾波算法對比仿真實驗結果如圖6和圖7所示。

圖6 桿臂估計誤差對比圖Fig.6 Comparison of lever arm estimation error

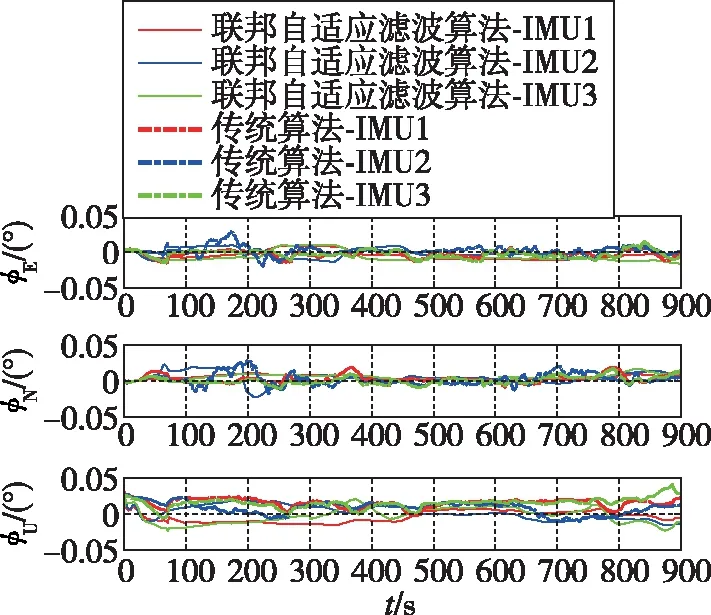
圖7 姿態估計誤差對比圖Fig.7 Comparison of attitude estimation error

傳統卡爾曼濾波算法和新型聯邦自適應濾波算法對比仿真實驗結果如圖8和圖9所示。

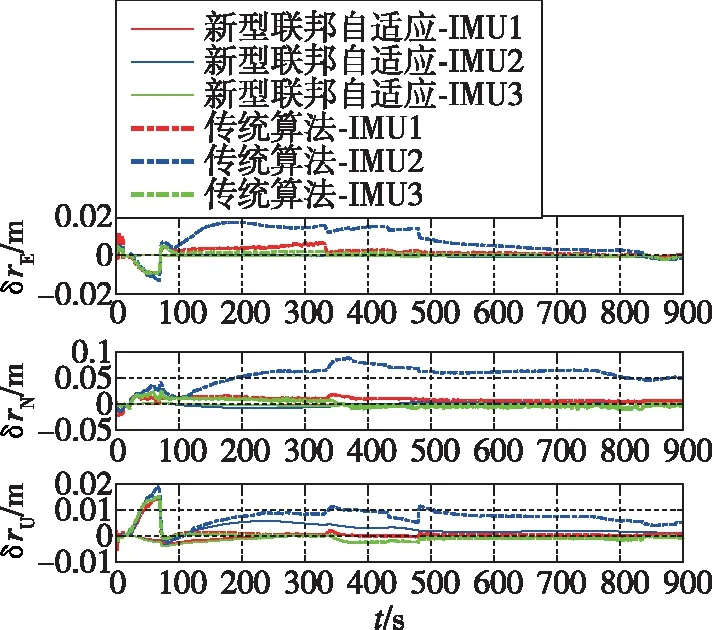
圖8 桿臂估計誤差對比圖Fig.8 Comparison of lever arm estimation error

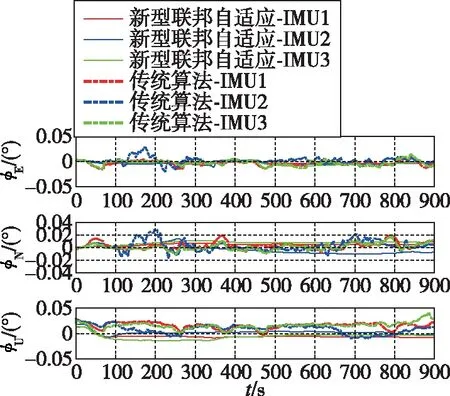
圖9 姿態估計誤差對比圖Fig.9 Comparison of attitude estimation error

將圖8、圖9和圖6、圖7進行對比可以看出，相較于傳統卡爾曼濾波算法以及子濾波器使用卡爾曼濾波的聯邦自適應濾波算法，新型聯邦自適應濾波算法可提高動態桿臂以及姿態估計的穩定性和精度。在卡爾曼濾波算法下，動態桿臂估計精度較差，姿態角估計穩定性較差，濾波器處于振蕩效果，并且航向角的估計精度較差。因此，算法效果主要以穩定性和動態桿臂、航向角的估計精度為評判標準。由于飛行過程中機翼振動和撓曲變形會導致量測信息噪聲時變，飛行環境的多變性則會導致受擾動較大。若使用傳統卡爾曼濾波方法無法有效進行桿臂和姿態的校正，誤差迅速增大，降低了傳遞對準的穩定性、快速性和精度。雖然使用聯邦自適應濾波算法可提高桿臂和姿態的估計精度，增加整體的抗擾動性能，但子濾波器估計的信息振蕩嚴重、收斂緩慢，且未考慮系統噪聲和量測噪聲的影響，傳入主濾波器后降低了信息融合的效果。本文提出的新型聯邦自適應濾波算法有效解決了上述問題。子濾波器中R自適應更新的加入，對時變噪聲有一定調節能力，可以正確估計Rk，實時調整增益K，P自適應更新的加入，對系統噪聲特性的影響進行削減，同時主濾波器進行信息融合，促進了整體濾波器的抗擾動性能，增強了校正效果。新型聯邦自適應濾波算法縮短了傳遞對準的時間，提高了傳遞對準的精度，增強了傳遞對準的穩定性。

為直觀分析提出方法的有效性，三種算法的動態桿臂及航向角估計的均方根誤差(Root Mean Square Error，RMSE)計算如表2和表3所示。選用RMSE作為評估標準，相較于傳統的卡爾曼濾波算法，新型聯邦自適應濾波算法用于分布式傳遞對準時動態桿臂估計精度提高了61.54%，航向角估計精度提高了42.35%。

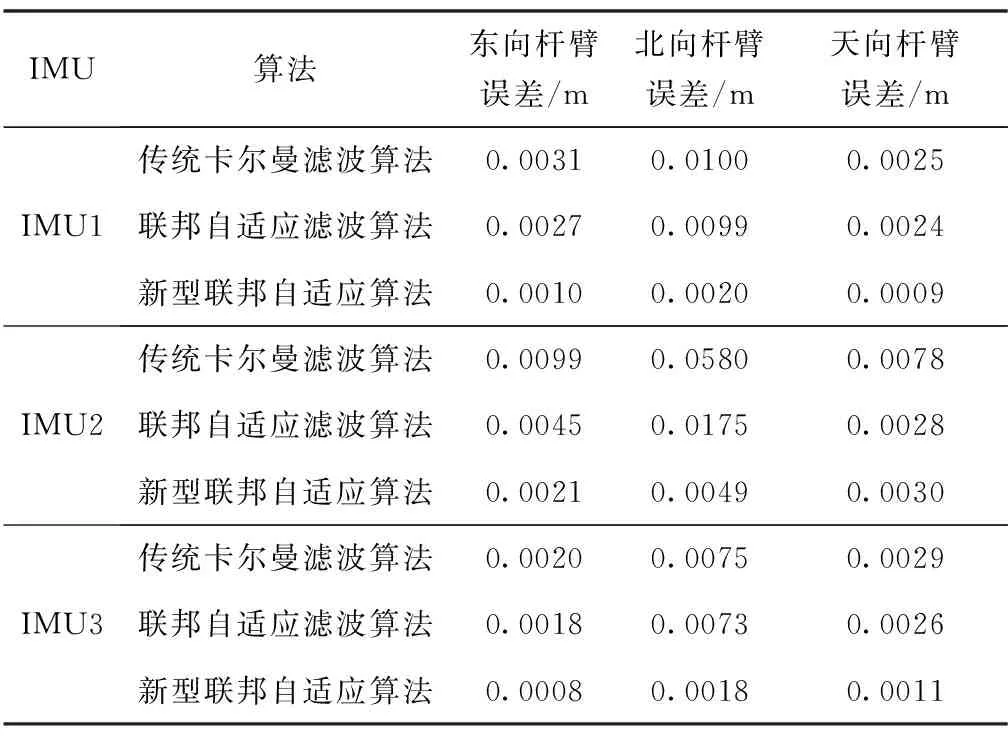
表2 桿臂估計誤差結果對比

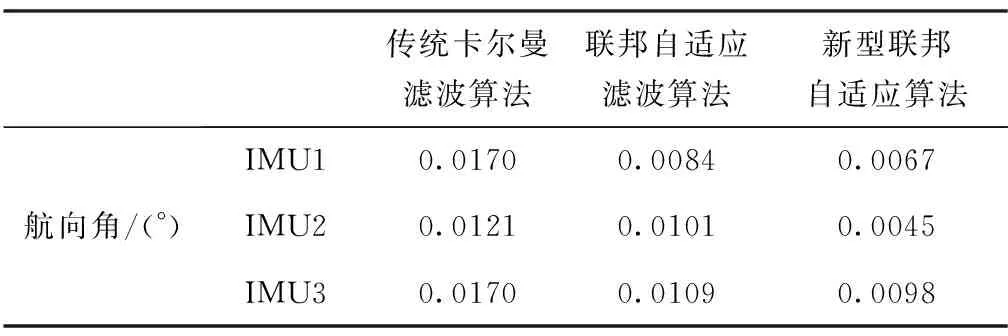
表3 航向角估計誤差結果對比

3 結論

針對分布式傳遞對準精度下降和穩定性問題，提出了子濾波器采用基于R和P自適應更新的卡爾曼濾波算法并結合27維傳遞對準模型用于主子傳遞對準，然后對不同子濾波器采用基于誤差協方差矩陣原則進行信息融合和權重分配。算法分析和實驗結果表明：新型聯邦自適應濾波算法中R自適應、P自適應以及信息融合方法的加入，抑制了量測信息噪聲時變特性對子濾波器的影響，緩解了狀態估計誤差對濾波的影響，提高了抗擾動性能，動態桿臂和姿態估計穩定性和精度得到了提高，證明了新型聯邦自適應濾波算法應用于分布式傳遞對準中的有效性。未來計劃建立更精確的傳遞對準建模，將陀螺儀和加速度計進行更深層次的展開和分析以提高精度。