含彈簧阻尼裝置空間機器人捕獲衛星分數階超扭滑模緩沖柔順控制

朱 安,陳 力

(福州大學機械工程及自動化學院,福州 350116)

1 引言

太空中大量的失效衛星使空間軌道資源被極大浪費,因此使用空間機器人對失效衛星進行回收受到廣泛關注[1-3]。與單臂空間機器人相比,雙臂空間機器人具有大載荷、高靈活性等優點,是捕獲操作研究的重點[4-6]。空間機器人捕獲衛星的過程大致可分為觀測、靠近、抓捕與鎮定控制4個階段。由于非合作衛星具有高速、旋轉特性,在抓捕階段其將與機器人末端執行器發生猛烈碰撞,由此產生的巨大沖擊力易造成機器人關節損壞,沖擊效應也會使鎮定控制更具挑戰,因此第3、第4 階段直接關系到捕獲操作的成功與否。

針對第3 階段,Lin 等[7]針對冗余空間機器人捕獲目標的碰撞問題,提出了一種由簡化阻抗控制器和增廣結構控制器組成的控制方案;Moosavian 等[8]為協調捕獲操作中基座、臂桿及目標航天器等各個系統,提出了一種多阻抗控制律;陳鋼等[9]利用碰撞過程中的沖量原理建立了碰撞動力學模型。然而在捕獲非合作衛星時,若未在脆弱的關節處添加保護措施,關節容易被沖擊載荷破壞。地面機械臂通常將串聯彈性執行器(Series Elastic Actuator,SEA)添加到關節處,以防止末端執行器與外界環境碰撞造成關節破壞。

針對第4 階段,Zhang 等[10]針對抓取大慣性非合作目標,提出了一種動量降低和動量再分配的協調控制方案;Wu 等[11]針對捕獲快速翻滾目標,設計了一種分解運動導納控制方法;Huang等[12]針對捕獲衛星后反作用輪結構發生變化,提出了一種改進的SDRE(Sate-Dependent Riccati Equation)最優控制器。滑模控制結構簡單、魯棒性強,被廣泛應用于各類系統的控制。但滑模控制也存在穩態誤差大、響應速度慢、奇異和抖振等缺點。為了解決這些問題,終端滑模控制采用非線性曲面,保證了魯棒性和快速收斂性[13-14],但抖振問題依然存在。超扭終端滑模可在保證高控制性能的同時,有效地消除抖振問題,近年來受到了廣泛關注[15-16]。此外,基于分數階的終端滑模控制,特別是速度、加速度等無法測量的系統中,可有效地提高系統快速收斂和軌跡跟蹤性能,且穩態誤差較小[17-18]。

綜上所述,為在空間機器人捕獲非合作衛星的過程中保護關節不受沖擊破壞,本文在關節電機與機械臂之間添加一種彈簧阻尼裝置(Spring Damper Device,SDD),相較于SEA,SDD既能利用彈簧實現沖擊載荷的快速緩沖、卸載,又可通過阻尼器抑制柔性振動。另外,針對關節受空間限制未能安裝速度、加速度傳感器導致無法測量速度、加速度的問題,通過三階觀測器對速度、加速度進行重構;針對捕獲后混合體系統的鎮定控制,提出一種匹配SDD 的分數階超扭滑模柔順控制策略,并利用數值仿真對該策略進行驗證。

2 SDD 模型結構與柔順策略

2.1 SDD 模型結構

SDD 的結構如圖1 所示,主要包含旋轉阻尼器與扭轉彈簧,且阻尼器嵌套在彈簧內部與彈簧同步運動。扭轉彈簧用于傳動與沖擊能量的吸收,旋轉阻尼器則提供阻尼力抑制柔性振動。圖1 中Ksk、Dtk(k =1,2,···,6)分別為SDD 中彈簧剛度與阻尼系數,Dmk、DLk分別為電機、機械臂端的等效阻尼系數。

圖1 SDD 結構Fig.1 Structure of the SDD

2.2 柔順策略描述

由于SDD 是被動裝置,捕獲非合作衛星時,沖擊效應將使混合體系統處于翻滾的狀態,此時若未對電機添加約束,產生的瞬時沖擊力矩很容易對關節造成損壞。為此,本文同時設置了電機的關閉與開啟閾值,其中關閉閾值用于限制瞬時沖擊力矩,開啟閾值可防止電機頻繁開關機。當檢測到沖擊力矩超過所設關機閾值后電機關閉,當SDD 將沖擊力矩降低到開啟閾值后電機將再次開啟。

3 動力學模型

雙臂空間機器人捕獲衛星如圖2 所示。圖2中,O0、Os、Oi分別為載體質心、衛星質心、各關節鉸中心,XOY為慣性參考坐標系,x0O0y0、xsOsys、xiOiyi分別為固定在載體質心、衛星質心、關節鉸中心上的坐標系。

圖2 配置SDD 的雙臂空間機器人與被捕獲衛星系統Fig.2 Dual-arm space robot with SDD and captured satellite system

參考文獻[19],可得配置SDD 的雙臂空間機器人捕獲衛星后的閉鏈混合體系統動力學模型為式(1):

式中:Mc∈R4×4為慣量矩陣,∈R4×1分別為包含科氏力、離心力列向量,Im∈R6×6為電機轉子轉動慣量矩陣,DLc∈R4×4為左臂等效阻尼系數矩陣,Dmg∈R6×6為電機等效阻尼系數矩陣,Dtg∈R6×6為阻尼器的阻尼系數矩陣,Ks∈R6×6為彈簧剛度矩陣。qc= [θ0,θ1,θ2,θ3]T,qg=[θ1,θ2,···,θ6]T,qm=[θm1,θm2,···,θm6]T,τc= [τ0,τ1,τ2,τ3]T,τg= [τ1,τ2,···,τ6]T,τm= [τm1,τm2,···,τm6]T。

捕獲目標衛星后混合體系統速度為式(2):

式中:qL= [x0,y0,qTc]T,qs= [xs,ys,θs]T,B∈R6×3,A、C∈R6×6為包含系統參數的矩陣。

碰撞沖擊力為式(3):

式中:fp= (Jr)+Mr[(t0+Δt)-(t0)] ,Jr∈R6×9為機械臂抓手捕獲點的運動雅克比矩陣,Δt為碰撞時長。

4 控制器設計

本文設計的分數階超扭滑模柔順策略既保持了傳統滑模結構簡單、對外界噪聲干擾和參數攝動魯棒性強的特點,同時也克服了穩態誤差大、響應速度慢、奇異和抖振等缺點,可較好地實現對碰撞后失穩的混合體系統快速、高精度的鎮定控制。

4.1 數階微分與積分

函數f(t)的Riemann-Liouville(RL)分數階微分與積分定義如式(4)、(5)所示[20]。

式中:r-1＜β ＜r,Dβ、Iβ分別表示分數階微分與積分,Γ(·)為Euler-Gamma 函數,其表達式如式(6)所示。

函數f(t)的分數階微分的n階導數為式(7)[20]:

4.2 三階觀測器設計

通常出于體積、質量、蓄電池電壓和成本等原因,空間機器人一般只裝有位置反饋器,而未裝有速度、加速度測量裝置。因此,本文利用位置反饋對速度、加速度進行重構。

將混合體系統模型改寫為式(8):

將速度、加速度重構為式(9)[21]:

假設1:觀測誤差與系統不確定項的和有界,如式(10)所示。

4.3 分數階超扭滑模策略

設計如式(11)所示形式的分數階超扭滑模面:

對式(11)求導可得式(12):

結合式(8)、(12)可得式(13):

基于式(1)、式(11),設計如式(14)所示形式的分數階超扭滑模控制器:

將式(14)帶入式(13),且結合假設1 可得式(15):

為實現系統穩定,將?的自適應率設計為式(16):

式中:σ＞0 為避免參數漂移的死區大小,γ＞0為增益系數,B= [1/ |S|1/2,01×7]T,ξ=[sgn(S)1/2,χ]T

設計如式(17)所示的Lyapunov 函數:

對ξ求導且代入式(15)可得式(18):

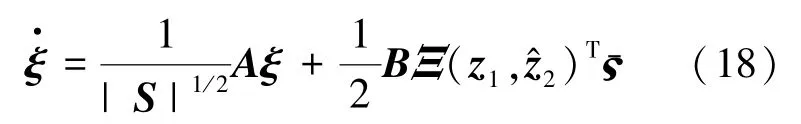
通過式(18)可得V的導數為式(19):

將式(16)帶入式(19)可得式(20):

通過式(20)可知系統穩定。

5 數值仿真分析

5.1 第3 階段SDD 抗沖擊性能模擬

雙臂空間機器人系統參數:m0= 200 kg,mi=10 kg(i =1,2,4,5),mj= 5 kg(j =3,6),Li= 2 m,Lj= 1 m,di= 1 m,dj= 0.5 m,I0= 128 kg·m2,Ii=15 kg·m2,Ij= 2 kg·m2,Imk= 0.05 kg·m2(k=1,2,…,6),ksk= 1000 N/rad,Dmk= 28.65 N·s/rad,Dtk= 1146 N·s/rad,DLk= 28.65 N·s/rad,ψ1=2.791 rad,ψ2= 0.349 rad。衛星參數:ms= 75 kg,ds= 0.5 m,Is= 9.5 kg·m2。空間機器人的初始位置為q= [10°,120°,- 60°,- 60°,60°,60°,60°]T。

為了驗證SDD 在第3 階段的抗沖擊性能,在多組衛星速度下對關節受到的沖擊力矩進行力學模擬,結果如表1 所示。衛星速度為= [xs,ys,θs]T,為沿x軸方向的線速度,為沿y軸方向的線速度,為繞z軸旋轉的角速度。

表1 不同衛星速度下SDD 抗沖擊性能對比Table 1 Comparison of impact resistance of SDD at different satellite velocities

由表1 可得,在第3 階段機器人捕獲不同速度的衛星,SDD 均能起到較好的緩沖作用,且最大可將碰撞沖擊力矩降低到52. 25%,因此認為SDD 在碰撞過程能很好保護關節。

5.2 第4 階段柔順策略性能模擬

系統控制參數:αn =2(n =1,2,3),β =0. 6,u =0. 8,σ =0. 01,γ =0. 1,K1=diag(50,50,50,50),K2= diag(40,40,40,40),K3= diag(10,10,10,10),K4= diag(10,10,10,10)。空間機器人的初始位置、速度與4. 1 相同,衛星速度q·s(0)= [0. 05,0. 05,8. 6]T,鎮定控制過程中混合體系統的期望狀態qd= [10,120,- 60,- 60,60,60,60]T。假設電機在發生碰撞1. 5 s 后開機。通過式(1)、(2)可計算出電機開機時混合體系統的位置q= [10. 44,120. 48,- 63. 57,- 52. 21,62. 82,52. 73,68. 94]T,仿真時間為15 s。

假設電機負載時關節能承受的沖擊力矩為170 N·m ,為了充分地保護關節,設置關機力矩閾值FC= 150 N·m ,開機力矩閾值FO=20 N·m。

仿真結果如圖3～圖7 所示。圖3 為鎮定控制過程中電機的開關機信號(1 表示開機,0 表示關機),圖4 為關節所受瞬時沖擊力矩變化,圖5為載體姿態角跟蹤軌跡,圖6 為左臂3 個關節角跟蹤軌跡,圖7 為右臂3 個關節角跟蹤軌跡。

圖3 電機開關機信號Fig.3 Switch signal of joint motor

圖4 關節所受沖擊力矩Fig.4 Impact torque on joints

圖5 載體姿態角軌跡Fig.5 Trajectory of the base attitude

圖6 左臂關節角軌跡Fig.6 Trajectory of left arm joint angles

圖7 右臂關節角軌跡Fig.7 Trajectory of right arm joint angles

結合圖3、圖4 可知,所提柔順策略在電機循環4 次關停后將瞬時沖擊力矩卸載,之后電機開始穩定輸出,且整個控制過程均未出現瞬時沖擊力矩超出關機閾值的情況。從圖5～圖7 可知,所提柔順策略可實現失穩混合體系統的快速收斂,且具有較高的控制精度。

6 結論

1)在末端執行器與目標衛星發生劇烈碰撞時,所設計的SDD 可很好地降低關節所受沖擊力矩,使空間機器人具備捕獲高速、旋轉衛星的能力。

2)配合SDD 設計的柔順策略可在鎮定控制過程中將關節所受瞬時沖擊力矩限制在安全范圍內,保護關節不受瞬時沖擊載荷的破壞,有利于實現捕獲操作過程的柔順化。

3)分數階超扭滑模控制可通過位置反饋對速度、加速度進行重構,解決了空間機器人無法測量速度、加速度信號的問題;所提算法魯棒性強,收斂速度快,控制精度高,對混合體系統鎮定控制具有一定的優勢。