工業機械臂的模型設計與運動分析

樊宏升

（北京天瑪智控科技股份有限公司，北京 100013）

隨著工業逐漸步入4.0時代，大幅提高了社會生產力，單純的人力已經無法滿足生產快速性與標準化的需求。特別是針對一些危險的工作環境，需要使用自動化機械設備取代人工進行更高效的生產。機械臂具有普適性，是生產線上代替人工的主要設備。

工業機器人作為機器人大家族的重要一員，主要指面向工業生產的或者有多個自由度的機器人或者機械臂。一般來說，工業機器人主要由機器人本體、操控機器人工作的控制器、伺服驅動系統及傳感系統組成。機器人不僅可以自動控制，也可以通過編程完成各工位的相應任務。在當今工業生產中，機械臂在提高產品良率和生產效率方面扮演了十分重要的角色。

1 機械臂運動控制算法研究現狀

機械臂軌跡跟蹤控制是機器人控制中最重要的部分。在應用機器人的過程中，既要系統功能完善，又要系統性能良好。前者體現在具有相對寬泛的運行空間范圍，后者表現在使用過程中能夠滿足人們的需求。機械臂具有和一般機器人相同的運動學和動力學特點，即變量多、時變性大、耦合性高等，運行中存在很多不確定因素，對整個控制系統的穩定性會產生很大影響。以五軸機械臂作為研究對象，基于設計的結構與尺寸進行運動學和動力學分析，并通過計算得到的運動學模型對機械臂進行實際仿真，規劃其運動軌跡，分析其空間運動范圍。

2 模型設計與計算

2.1 模型設計

本機械臂是一種關節坐標式機器人，如圖1所示。它主要由旋轉底座部分（肩膀）、大臂部分、前臂部分及機頭部分（手腕部分）4部分組成。

圖1 機械臂模型

2.2 各個關節的力矩估算

各個關節的動力參數是選擇電機型號和減速器減速比的重要依據。根據機械臂動力學的相關知識，完整的機器人動力學方程為[1]

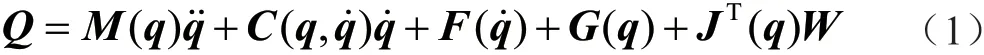
式中：q、q˙、˙˙q分別為廣義關節坐標角度、速度和加速度矢量；M(q)為關節空間慣性矩陣；C為科里奧利和向心耦合矩陣；F為摩擦力；G為重力載荷；Q為關節驅動力矩；W為施加在末端執行器的外力；J(q)為機器人的雅可比矩陣[2]。

為估算每個關節的最大力矩，假定各個關節的重量都集中在關節理論中心點，各個連桿的重量都集中在連桿中間。計算靜力矩時，機械臂主要受到重力產生的力矩作用，將機械臂拖動至產生最大力矩的位置，如圖2所示。

圖2 機械臂伸展圖

機械臂位于最長伸展距離時，夾持處與大臂電機的垂直距離為1 091 mm，近似為1.1 m，計算可得大臂驅動關節距離計算質心距離為0.55 m。大臂質量為2 kg，前臂質量為1.54 kg，手腕部分質量為2.5 kg，設計指標夾取的物件質量為2 kg，此時前臂驅動關節距離最遠處距離為685 mm，計算可得前臂驅動關節距離計算質心距離為0.34 m。前臂質量為1.54 kg，手腕部分質量為2.5 kg，設計指標夾取的物件質量為2 kg，則第3個前臂驅動關節的計算力矩為

旋轉底座電機與腕部旋轉電機驅動部分不受重力扭矩，主要是加速度扭矩作為負載驅動整個機械臂的旋轉。這時最大扭矩等于轉動慣量乘以角加速度，即

轉動慣量的表達式為

機械臂的質量為8.04 kg，桿長為1.1 m。假設機械臂旋轉底座最大角加速度為0.5 rad·s-2，此時旋轉平臺關節的最大扭矩值為

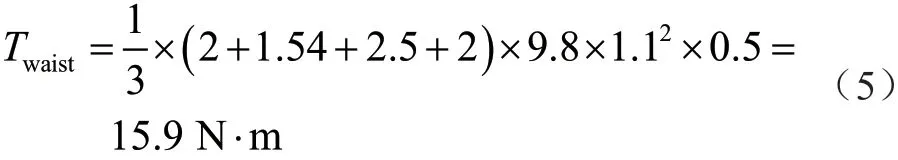
夾具質量為0.8 kg，夾持物件質量為2 kg，腕關節最大角加速度為1 rad·s-2，得出腕關節的最大扭矩值為

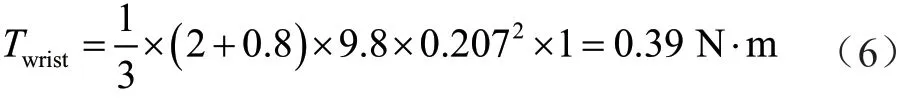
3 機械臂運動學分析

機械臂的運動學研究的是機器人的運動特性，從以下兩個問題出發進行分析：一是正運動問題，即已知機械臂的連桿參數和關節變量，確定執行坐標系的位置和姿態；二是逆運動問題[3]，即已知機械臂連桿參數，給定目標為固定姿態，確定關節變量的大小。

3.1 機械臂的正運動學分析

正運動學的求解是根據已知關節變量求末端執行端相對于參考坐標系位姿的過程。正運動學對于軌跡規劃與軌跡跟蹤控制具有重要意義。通過改進D-H方法確立連桿參數的變換關系，將機器人極坐標系通過連桿齊次矩陣的連乘變換到末端執行器坐標系。利用這種變換可以求解機器人機械臂執行端相對于機器人基座的坐標系位置。三維向量n、o、a分別表示在基礎坐標系下的向量相對變換。機械臂的正運動學方程可以根據表述的關系式求解，整理化簡后為

3.2 機械臂的逆運動學分析

正運動學研究的是已知各關節角度[4]，計算執行器末端在笛卡爾空間中的位置。逆運動學主要研究的是給定執行器末端在笛卡爾空間中的位置，計算各個關節角的角度位置。

從工程應用角度來說，待給定各個關節角變量后，正運動學有特定唯一的解，此時末端姿態是唯一確定的。但是，逆運動往往有很多種結果。由于機器人結構設計，nz、oz、ax、ay都等于0，az=1。若末端的位姿已給定，可以求解關節變量θ1、θ2、θ3、θ4、θ5的值。

求解θ1為

求解θ2。在式（8）第一個等式兩邊依次分別乘有θ23為

所以，有

求解θ3為

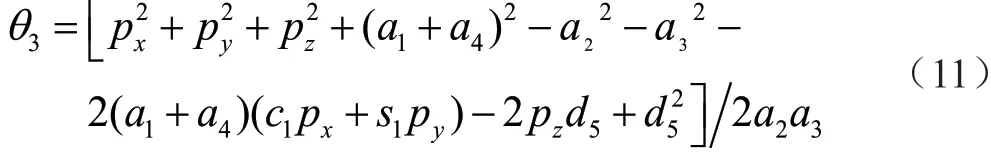
求解θ4。由提及的機械結構設計可知，θ4滿足關系

于是，有

求解θ5。在式（8）第一個等式兩邊依次分別乘

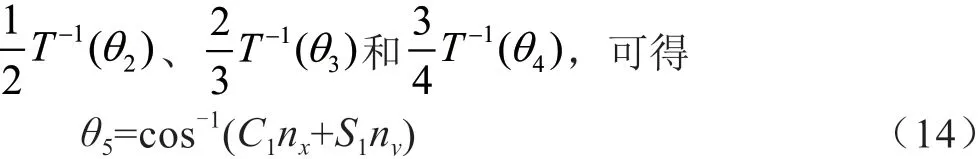
4 機械臂運動學仿真分析

分析工業機械臂的運動學、動力學以及軌跡過程，可以使用基于MATLAB平臺開發的機器人工具箱。

4.1 正運動學仿真

使用工具箱中的函數對工業機械臂建模并進行正運動學仿真，仿真結果見圖3。可以給定角度進行示教調節，通過軟件中的滑塊控制角度的輸入值，實現實時仿真控制。

圖3 正運動仿真結果

4.2 逆運動學仿真

使用工具箱中的函數對機械臂求逆解。先給每個軸給定角度，計算此刻的變換矩陣，再將這個變換矩陣代入逆解函數，給定目標位置與姿態。

5 機械臂運動空間分析與仿真

使用蒙特卡洛方法分析工作空間。蒙特卡洛屬于模擬統計方法[5]，是一種以概率統計理論為指導的數值計算方法。先在機械臂關節運動范圍內生成n個隨機值，關節角的取值為θi=θimin+(θimax-θimin)*rand(1,n)，再將隨機生成的角度值代入計算得到的正運動學方程，最后在MATLAB中將機械臂的工作空間顯示為點云圖，取隨機值個數為20 000進行計算分析。機械臂的工作空間如圖5所示。使用蒙特卡洛方法在MATLAB中模擬其工作空間，使得實際機械臂的使用更加準確直觀。

圖4 逆運動仿真結果

圖5 機械臂模擬工作空間

6 結語

本文闡述工業機器臂的應用領域與發展現狀，主要介紹機械臂的機械結構設計，標定機械臂的主要設計尺寸，并通過計算機械臂每個軸承受的最大力矩范圍來選定滿足條件的步進電機與減速器。分析機械臂的運動學相關內容時，簡單介紹機械臂坐標變換的基礎知識、位姿在空間的描述、齊次坐標矩陣的平移與旋轉。以設計的機械臂為研究對象，使用改進D-H方法對機械臂進行數字化建模，并對其正運動學與逆運動學進行分析，最后使用蒙特卡洛方法對機械臂的空間運動范圍進行計算。現階段，5自由度工業機械臂的動力學模型建立還存在一定誤差，仍需尋找更加精確且有效的化簡方法，使化簡得到的動力學方程滿足實時軌跡跟蹤的控制要求。