一種雙密封結構穩定漏率判定方法

龍 偉，趙肆方，楊才華，王隆基，李文靜

（中國航天員科研訓練中心，北京 100094）

0 引言

雙密封結構大量應用于航天產品的密封結構中，雙密封結構產品在進行氦質譜檢漏時，不管是用氦質譜壓力真空檢漏，還是吸槍法單點檢漏，常常出現示漏氣體漏率緩慢爬升的現象，兩道密封處的初始漏率越小，穩定平衡時間越長。針對雙密封結構漏率測試的時間以及穩定漏率的判定，目前沒有明確統一的方法，導致檢漏結果不一致，特別是在穩定漏率略超出允許漏率，導致產品拒收時，分歧尤為突出[1-2]。

本文提出一種穩定漏率判定方法，通過建立漏率的增長模型，合理確定檢漏時間，可以在示漏氣體漏率曲線未平衡穩定的情況下預判穩定漏率，提高檢漏效率。

1 雙密封結構泄漏規律

1.1 雙密封結構泄漏模型及數值分析

雙密封結構原理和泄漏示意圖如圖1、2所示。恒壓輸入的示漏介質（純氦）首先經過第一道密封（密封1）進入到兩密封間的容積Vc，然后再經過第二道密封（密封2）進入氦質譜檢漏儀。容積Vc初始狀態下存有壓力為常壓、體積為Vc的空氣。

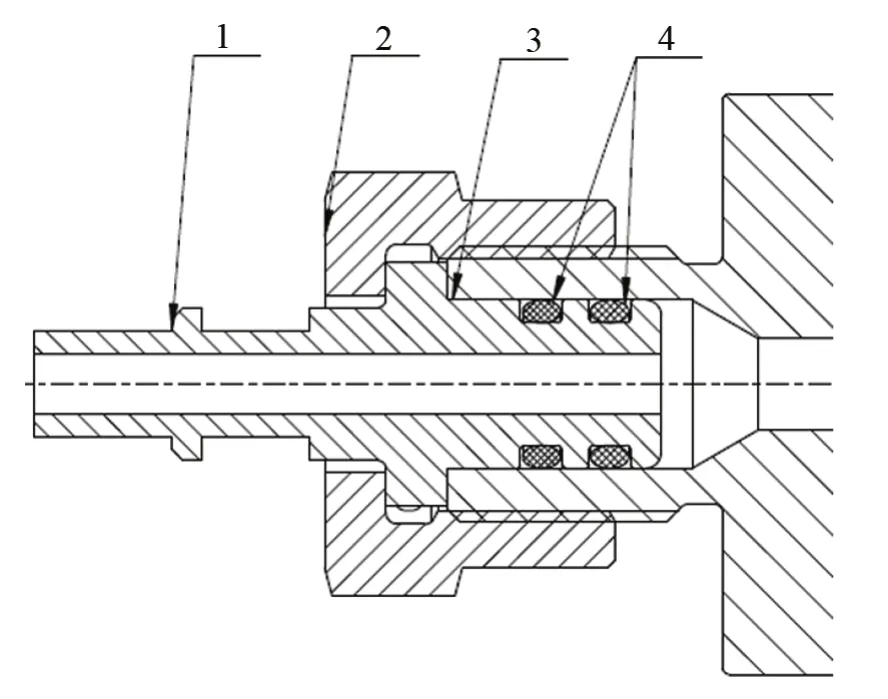
圖1 雙密封結構原理圖Fig.1 Schematic diagram of double sealed structure

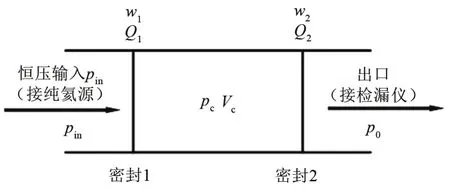
圖2 雙密封結構泄漏示意圖Fig.2 Leakage diagram of double sealed structure

雙密封結構在檢漏時，漏率不穩定的原因主要包括：

（1）由于氦質譜檢漏儀只對氦信號有反應，隨著檢漏時間的延長，容積Vc內的氦濃度逐漸升高，氦分壓逐漸增大，示漏氣體漏率因此逐漸增大；

（2）由于密封1和密封2兩處的漏率不同，容積Vc內的壓力會發生變化，從而引起密封1和密封2處的漏率發生變化。

因此，雙密封結構的泄漏過程與兩道密封之間的容積Vc、密封1和密封2的漏率、容積Vc內的壓力等都有密切關系[3]。

以分子流為例，密封件漏孔漏率與壓差成正比，忽略溫度和漏孔兩端分子量平均值對漏率的影響以及示漏氣體的擴散時間，輸入氣源為恒定壓力的高純氦氣。氣路系統與電路系統類似，氣容等效于電容，流阻等效于電阻，氣壓等效于電壓，兩者有類似的模型，遵循相似的規律。因此，利用電路等效氣路的方法以及氣路相關理論約束[4-6]，建立氦質譜壓力真空檢漏法檢漏的氣路模型，如圖3所示。雙密封結構系統參數如表1所列。

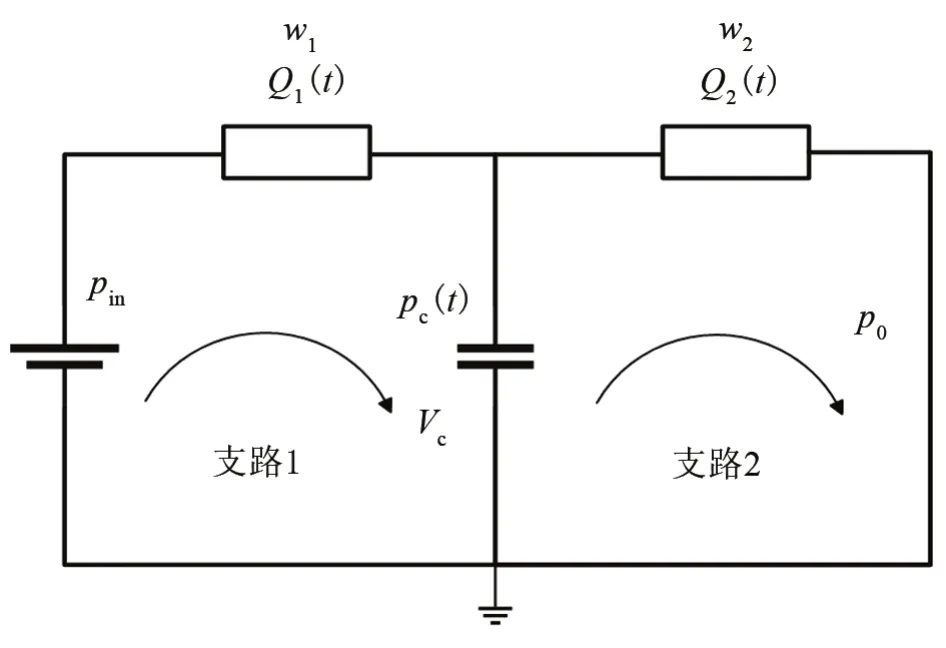
圖3 氦質譜壓力真空檢漏法檢漏的氣路模型圖Fig.3 Gas path model of helium mass spectrometer pressure vacuum leak detection

表1 雙密封結構系統參數Tab.1 System parameters of double sealed structure

根據漏率和壓力、流阻的關系及氣體量守恒，對圖3模型做如下分析（式（1）～（4））：

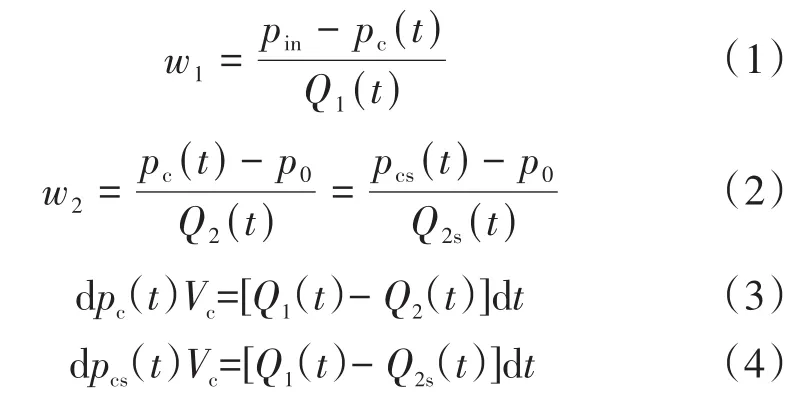
整理后，可得到雙密封結構密封1漏率、密封2漏率、兩密封間容積內壓力、氦分壓隨時間變化的數學模型（式（5）～（8））：

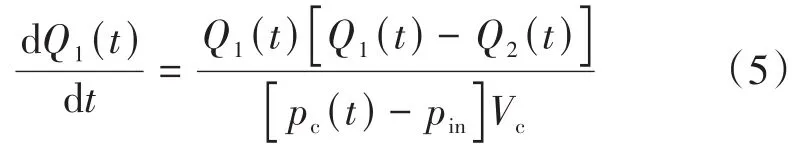
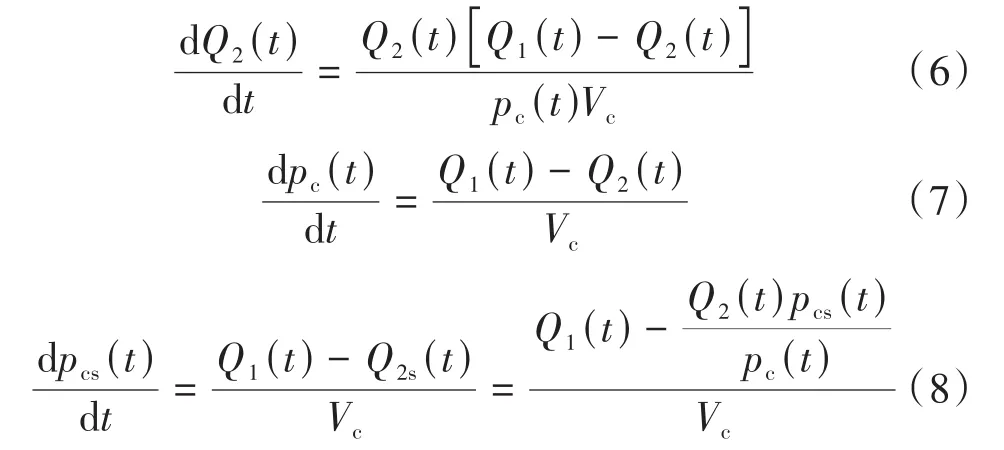
求解式（5）～（8）組成的一階常系數線性微分方程組，再根據式（2）即可求得示漏氣體漏率隨時間的變化關系。假設某產品的Vc約為7.5 mm3，利用氦質譜壓力真空檢漏法檢漏時，pin=4.04×105Pa。利用四階龍格—庫塔法求解由式（5）～（8）組成的微分方程組，編制程序求得在Q1（密封1漏率）、Q2（密封2漏率）不同的初始值下的計算結果，如表2所列。

表2 不同初始漏率下的穩定時間、穩定壓力及穩定漏率Tab.2 Stable time，stable pressure and stable leakage rate under different initial leakage rates

從表 2 可以看出，當Q1=1.0×10-6Pa·m3/s、Q2=1.0×10-6Pa·m3/s，漏率穩定時間為 90 min；Q1=1.0×10-7Pa·m3/s、Q2=1.0×10-7Pa·m3/s，漏率穩定時間為875 min；Q1=1.0×10-8Pa·m3/s、Q2=1.0×10-8Pa·m3/s，漏率穩定時間為8 725 min。可以看出，示漏氣體漏率的穩定是個緩慢的過程，特別是在每道密封漏率都很小的情況下，這個過程時間更長。后文1.2節試驗測試數據和數值分析結論一致。利用吸槍法單點檢漏時，也觀察到類似的現象[5-6]，這進一步證明建立的數學模型的正確性。

1.2 雙密封結構漏率測試分析

利用氦質譜壓力真空檢漏法，測試了三個雙密封結構產品的漏率，測得穩定漏率分別為1.0×10-6Pa·m3/s、1.3×10-7Pa·m3/s和 5.4×10-8Pa·m3/s，其示漏氣體漏率曲線分別如圖4～6所示。可以看出，穩定漏率越小，穩定時間越長。當穩定漏率為1.0×10-6Pa·m3/s的雙密封結構產品檢漏時，漏率穩定時間約90 min；當穩定漏率為 1.3×10-7Pa·m3/s時，漏率穩定時間約1 810 min；當穩定漏率為5.4×10-8Pa·m3/s時，漏率穩定時間約2 700 min。

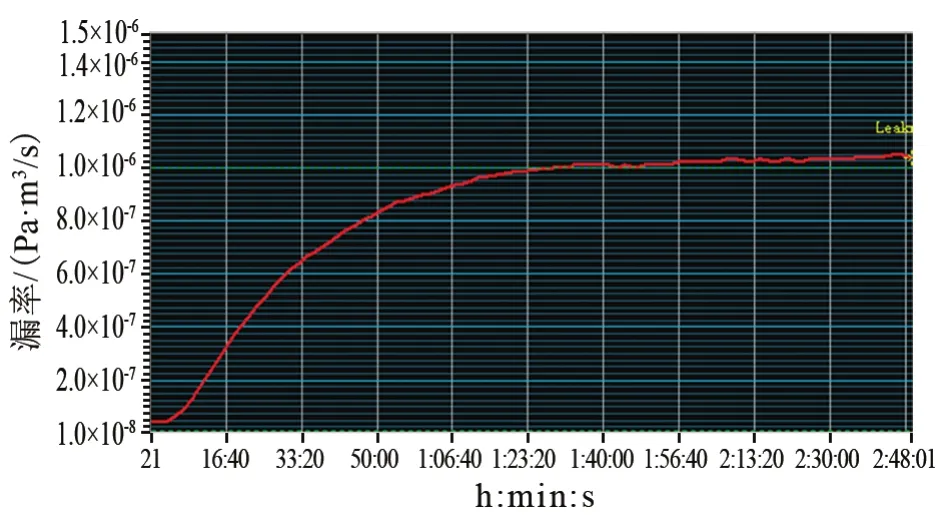
圖4 穩定漏率值為1.0×10-6Pa·m3/s的示漏氣體漏率曲線Fig.4 Leakage rate of indicator gas（stable leakage rate value：1.0×10-6Pa·m3/s）

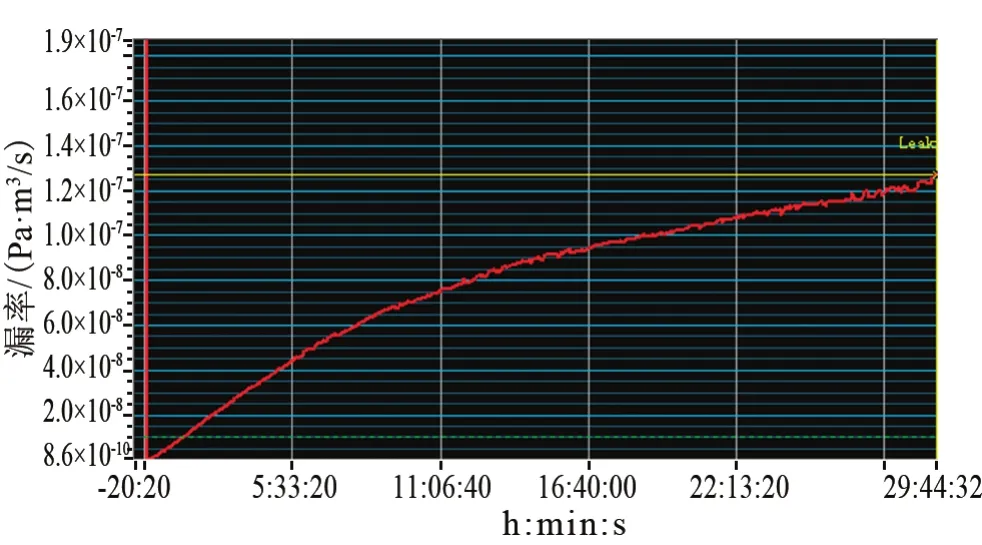
圖5 穩定漏率值為1.3×10-7Pa·m3/s的示漏氣體漏率曲線Fig.5 Leakage rate of indicator gas（stable leakage rate value：1.3×10-7Pa·m3/s）

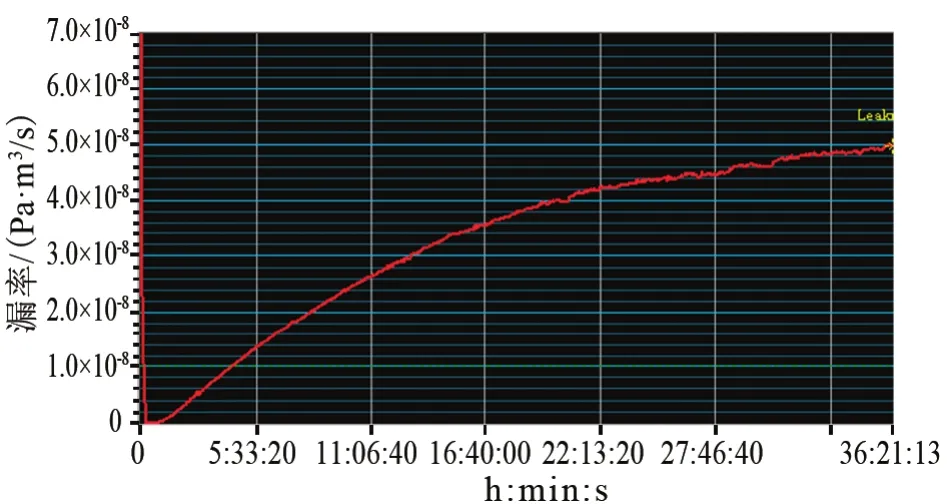
圖6 穩定漏率值為5.4×10-8Pa·m3/s的示漏氣體漏率曲線Fig.6 Leakage rate of indicator gas（stable leakage rate value：5.4×10-8Pa·m3/s）

2 穩定漏率快速判定

2.1 穩定漏率快速判定方法

通過建立的雙密封結構數學模型可知，示漏氣體漏率隨時間變化關系的數學表達式是一階常系數線性微分方程。根據一階常系數線性微分方程的通解公式可知其解為自然常數為底的指數函數類型。根據產品漏率測試曲線，發現雙密封結構的漏率隨時間呈指數增長，并且在初始時刻，示漏氣體漏率近似為0，在測試曲線末端，示漏氣體漏率趨于穩定。因此，采用Q（t）=a+be-t/c（a，b，c為常數）的指數函數式，建立示漏氣體漏率隨時間變化的近似數學關系。利用python軟件編程對不同時間段的實測漏率值按所選定的指數函數進行曲線擬合[7-8]，得到a，b，c等3個擬合常數。

不斷增加測試時長，可得到一系列a1，a2，a3，…，an值（即穩定漏率預測值），當相鄰兩次測試a值的擬合誤差（擬合誤差=[（an+1-an）/an+1]×100%）不大于給定的控制值時，即可認為an+1值就是漏率的穩定測量值。當t→∞，a與漏率真值間的誤差趨于0。按照該方法，就可以大幅縮短獲得在允許誤差范圍內穩定漏率的時間，提高測試效率。

由于檢漏初始的幾分鐘，因受檢漏系統本底、被檢件初始狀態等因素影響，不選取采樣點。

2.2 實例應用與分析

利用2.1節所述方法分別對圖4～6的漏率曲線進行分析擬合，曲線擬合結果分別如圖7～9所示。穩定漏率預測值與試驗值對比如表3～5所列，表中擬合誤差（（an+1-an）/an+1×100%）為相鄰兩個取樣間隔擬合值的相對變化量，相對誤差（[（穩定漏率預測值-穩定漏率試驗值）/穩定漏率試驗值]×100%）為利用指數函數擬合的穩定漏率預測值與穩定漏率試驗值間的相對偏差值。

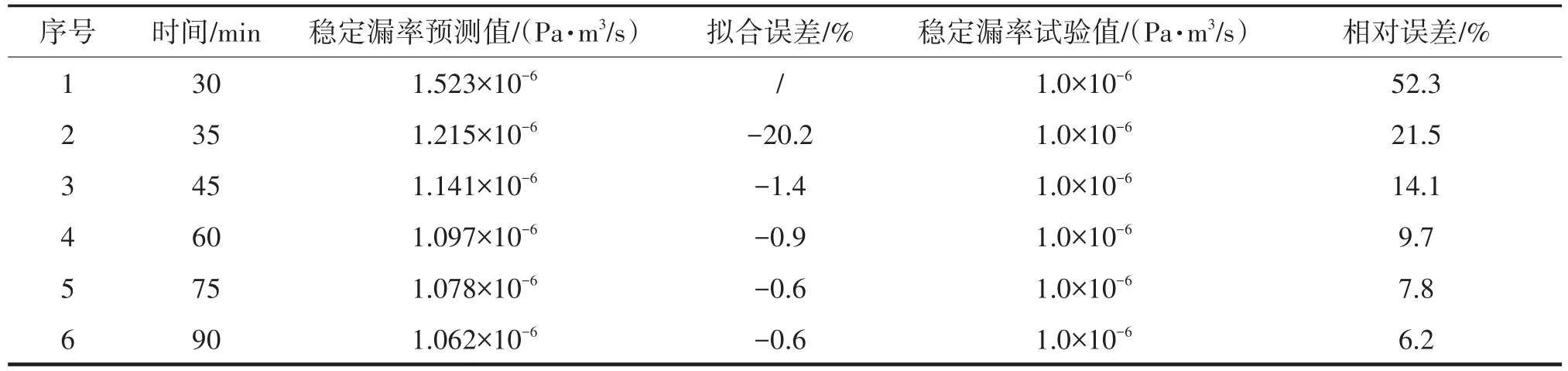
表3 穩定漏率預測值和試驗值對比（穩定漏率值：1.0×10-6Pa·m3/s）Tab.3 Comparison for predictive value of stable leakage and test stabilized leakage rates（stable leakage rate value：1.0×10-6Pa·m3/s）

針對穩定漏率為1.0×10-6Pa·m3/s的測試數據，數據點每隔5 min進行取值。不同時間段的擬合曲線如圖7所示，穩定漏率預測值與試驗值對比如表3所列。從圖7和表3可以看出，隨著測試時間的延長，擬合誤差絕對值和相對誤差整體趨勢逐漸減小。當雙密封結構產品的穩定漏率為1.0×10-6Pa·m3/s時，試驗穩定時間約90 min，利用本文方法預測穩定漏率，當允許誤差分別為20%、10%時，預測穩定漏率所用測試時間約為40 min、60 min，檢漏效率能提高約55%、33%。

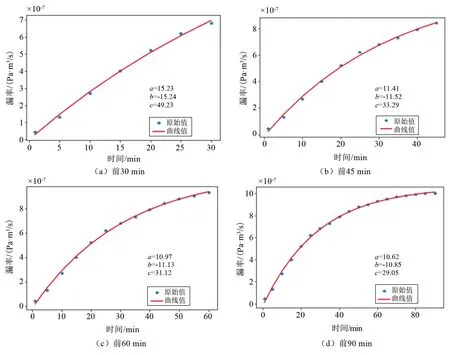
圖7 穩定漏率為1.0×10-6Pa·m3/s的雙密封結構不同周期的漏率擬合曲線Fig.7 Fitting curves of leakage rates for different periods of double sealed structures with stable leakage rate of 1.0×10-6Pa·m3/s

針對穩定漏率為1.3×10-7Pa·m3/s的測試數據，采用同樣方法進行擬合。前600 min內采樣間隔為20 min，600 min之后采樣間隔為30 min。不同時間的擬合曲線如圖8所示，穩定漏率預測值與試驗值對比如表4所列。從圖8和表4可以看出，隨著測試時間的延長，擬合誤差絕對值和相對誤差整體趨勢均逐漸減小。當雙密封結構產品的穩定漏率為 1.3×10-7Pa·m3/s，試驗穩定時間需要約1 810 min。利用本文方法預測穩定漏率，當允許誤差分別為30%、20%、10%時，漏率測試時間分別為520 min、660 min、840 min，檢漏效率能提高分別約71%、63%、53%。

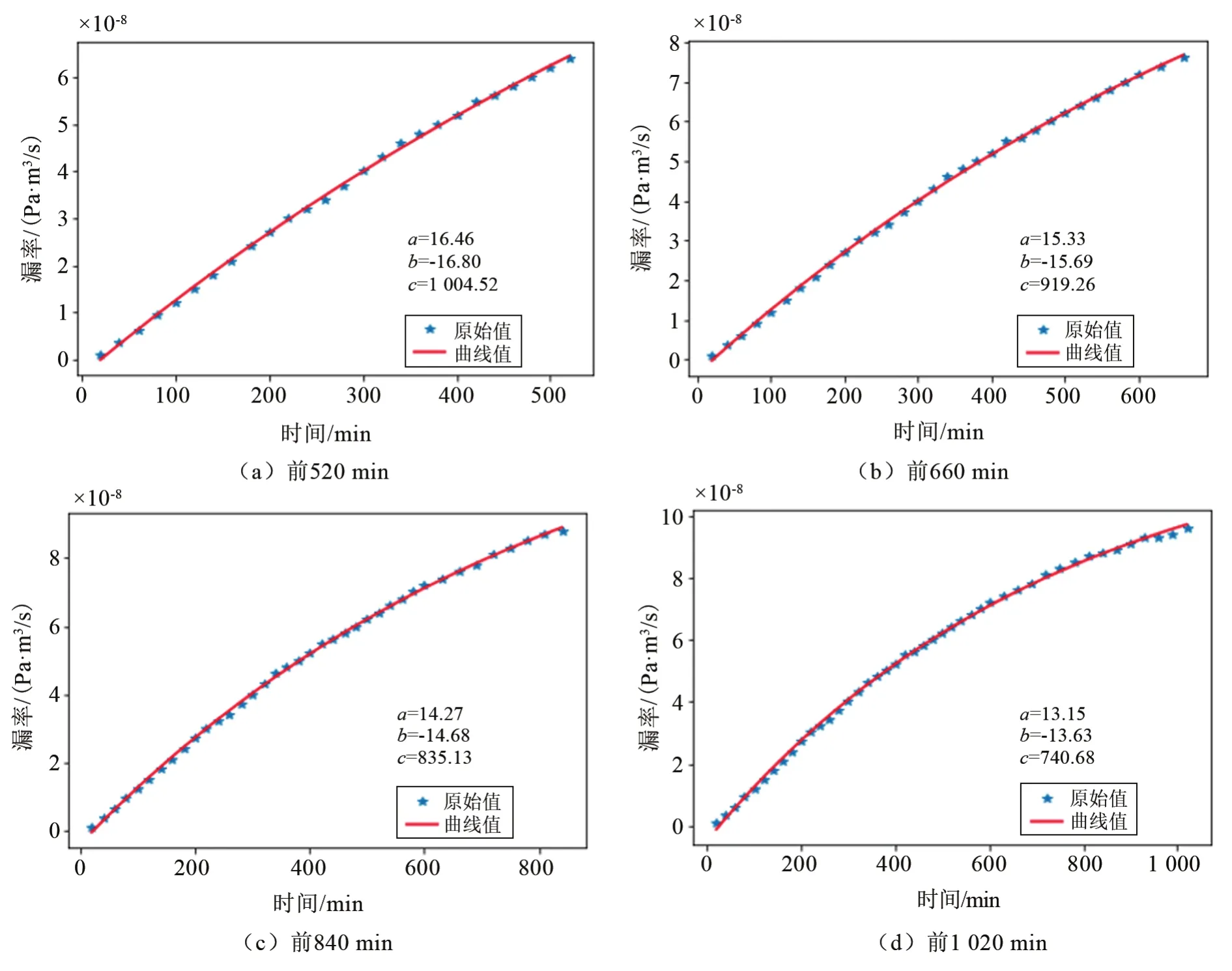
圖8 穩定漏率為1.3×10-7Pa·m3/s的雙密封結構不同周期的漏率擬合曲線Fig.8 Fitting curves of leakage rates for different periods of double sealed structures with stable leakage rate of 1.3×10-7Pa·m3/s

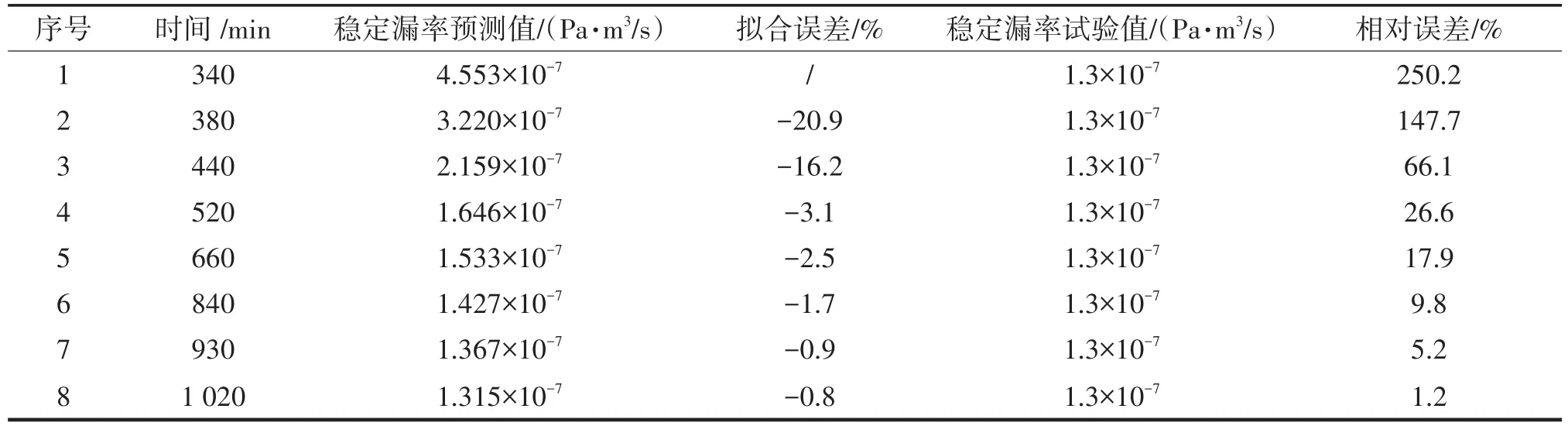
表4 穩定漏率預測值和試驗值對比（穩定漏率值：1.3×10-7Pa·m3/s）Tab.4 Comparison for predictive value of stable leakage and test stabilized leakage rates（stable leakage rate value：1.3×10-7Pa·m3/s）

針對穩定漏率為5.4×10-8Pa·m3/s的數據，采用同樣方法進行擬合。前600 min內采樣間隔為20 min，600 min之后采樣間隔為30 min。不同周期的擬合曲線如圖9所示，穩定漏率預測值與試驗值對比如表5所列。

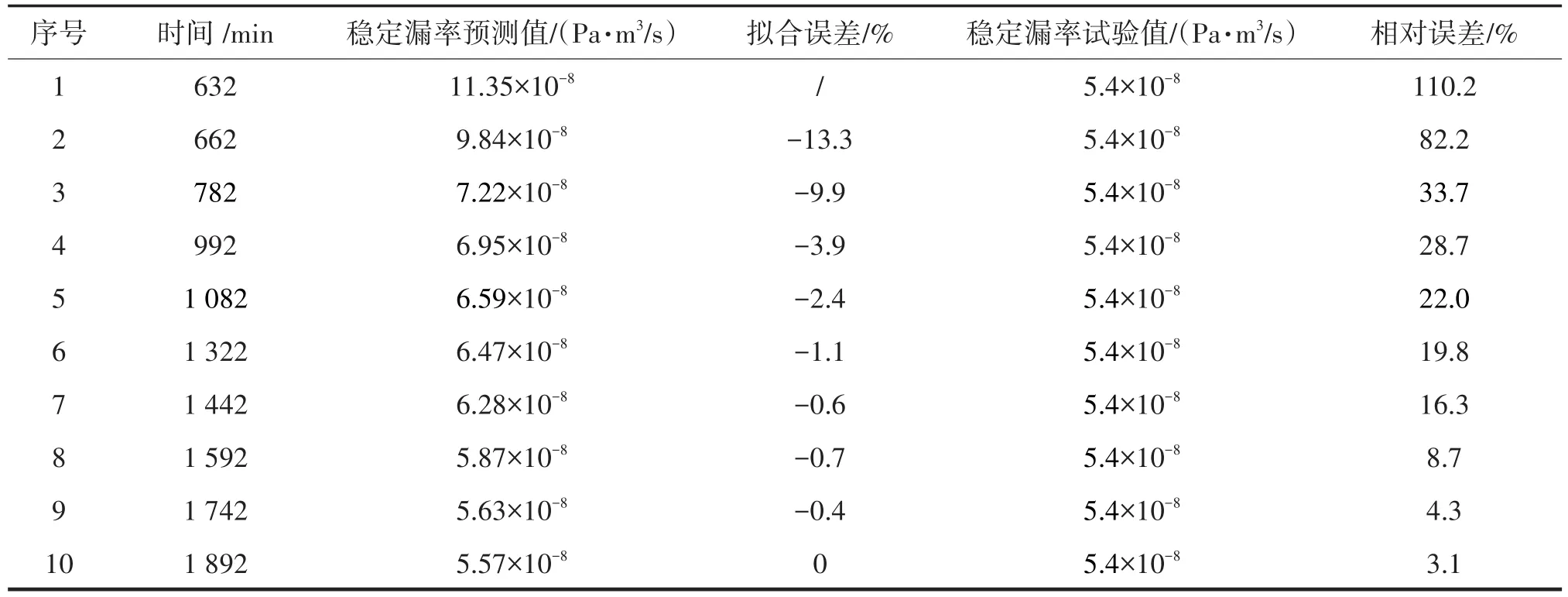
表5 穩定漏率預測值和試驗值對比（穩定漏率值：5.4×10-8Pa·m3/s）Tab.5 Comparison for predictive value of stable leakage and test stabilized leakage rates（stable leakage rate value：5.4×10-8Pa·m3/s）

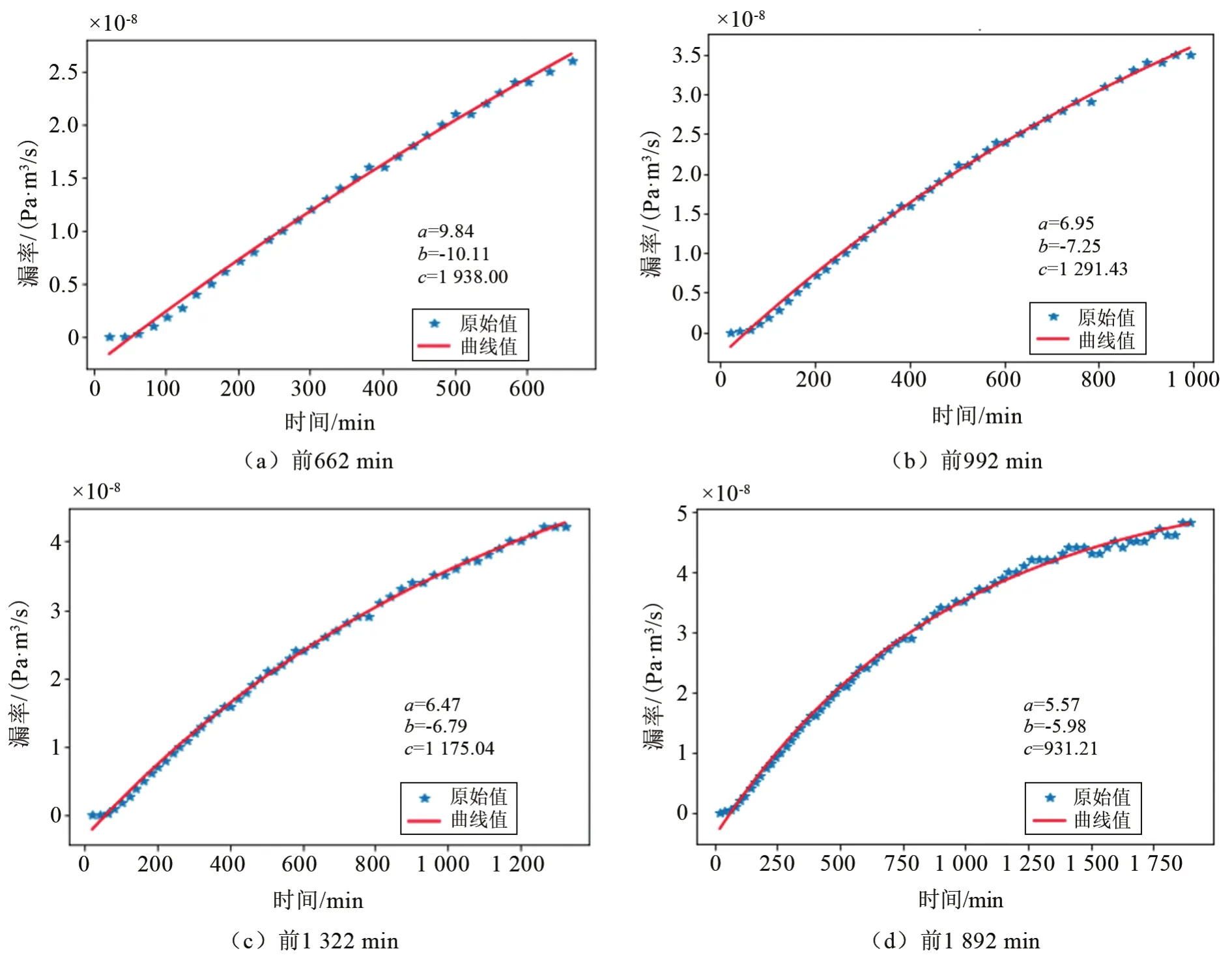
圖9 穩定漏率為5.4×10-8Pa·m3/s的雙密封結構不同周期的漏率擬合曲線Fig.9 Fitting curves of leakage rates for different periods of double sealed structures with stable leakage rate of 5.4×10-8Pa·m3/s

從圖9和表5可以看出，與前兩個實例類似，隨著測試時間的延長，擬合誤差絕對值和相對誤差整體趨勢亦逐漸減小。當雙密封結構產品的穩定漏率為5.4×10-8Pa·m3/s，試驗穩定時間需要約 2 700 min，利用該方法預測穩定漏率，當允許誤差分別為30%、20%、10%時，預測穩定漏率所用測試時間約為992 min、1 322 min、1 592 min，檢漏效率能提高約63%、51%、41%。

2.3 應用判定方法的幾點建議

本文中的雙密封結構，在壓力真空法檢漏時，其穩定漏率一般都在1.0×10-6～1.0×10-8Pa·m3/s區間內。在實際應用中，本判定方法的應用與檢漏時間的確定按如下建議進行：

（1）對某種產品第一件檢漏時，檢漏時間為直到示漏氣體漏率曲線漏率顯示穩定時為止，獲取完整的示漏氣體漏率曲線和試驗數據；

（2）如文中實例一樣，對第一件產品的示漏氣體漏率曲線，在不同檢漏時間段內采樣后分別進行函數擬合，得到不同檢漏時間的穩定漏率預測值，并計算相對誤差；

（3）該種產品其余件檢漏，應用第一件產品示漏氣體漏率曲線的擬合分析結果，根據可接受的相對誤差來確定該件產品的檢漏時間，然后在該檢漏時間內對示漏氣體漏率曲線采樣，按照本文方法進行函數擬合，得到預測穩定漏率值即為本次檢漏的穩定漏率值；

（4）若出現同種產品示漏氣體漏率曲線偏離較大時，檢漏時間就以示漏氣體漏率曲線漏率顯示穩定時為止。

3 結語

對雙密封結構產品進行氦質譜壓力真空法檢漏時，應用文中指定函數類型進行曲線擬合的方法來預測穩定漏率，能縮短示漏氣體穩定漏率的判定時間，極大提高檢漏效率，特別是對于10-7Pa·m3/s、10-8Pa·m3/s量級的微漏產品。實際應用中，可根據經驗證實的應用實例及可接受的相對誤差來確定檢漏時間，既保證漏率測試的準確性，又能提高檢漏效率，對雙密封結構產品檢漏工作具有一定的指導意義。后續工作有待進一步探索更加合適的擬合函數，在更短的測試時間內減小穩定漏率預測相對誤差，進一步提升檢漏效率。