基于Kronecker積的差分波束形成

劉文俊，鞏朋成*，吳云韜

1.智能機器人湖北省重點實驗室（武漢工程大學），湖北 武漢 430205；2.武漢工程大學計算機科學與工程學院，湖北 武漢 430205

波束形成本質上是一種空間濾波器，對麥克風陣列接收到的信號進行加權，在接收到的來自期望信號方向形成主波束，對接收到的其他方向的干擾信號進行抑制［1-2］。近幾十年來，許多專家學者投入到對該領域的研究和探索，形成了許多關于波束形成的分支，常見的包括延遲求和波束形成（delay-sum beamformer，DSB）［3］、超指向性波束形成（super-directive beamformer，SDB）［4］、自適應波束形成（adaptive beamformer，AB）［5］、差分波束形成（differential beamformer，DB）［6］等等。

其中，差分波束形成算法是當前的一個研究熱點。差分麥克風陣列不同于加性麥克風陣列（將麥克風陣列接收到的信號進行相加），它利用麥克風陣列中相鄰的麥克風的聲壓差來實現波束形成，相較于加性麥克風陣列，差分波束形成具有高指向性增益和能形成波束圖不隨頻率而改變的優點。因此，使用差分波束形成算法來處理像語音信號這種頻率波動大的信號，具有其獨特的優勢。另外，差分麥克風陣列中的相鄰2個麥克風之間間距較小，致使整個麥克風陣列所占的空間較小，這就方便了它嵌入到小設備中，為差分麥克風陣列的實際應用提供了方便。

最初，差分波束形成是采用多層結構的形式來設計的，一個高階的差分波束形成器通常由多個低階的差分波束形成器組成［7］。但是，這種傳統的波束形成缺乏靈活性，存在失配問題，而且在低頻時對傳感器噪聲和麥克風陣列自身的缺陷非常敏感。為了克服以上缺陷，在文獻［8］中，通過短時域傅里葉變換來形成差分波束形成的方法被提出，這個方法將傳統的求解波束形成問題轉化為在零陷約束下對線性結構優化求解的問題。隨著波束形成技術的發展，出現了一種利用空間差分算子來設計波束形成的方法［9］。這種利用空間差分算子來設計波束形成的方法在白噪聲增益和指向性因子之間進行了折衷。設計的波束形成器在各個方面的表現更加均衡。

另外，Kronecker積的方法應用在多輸入多輸出（multiple-input multiple-output，MIMO）雷達波束形成領域［10］，為設計差分波束形成提供了新的思路［11］，Kronecker積是將一個較大的麥克風陣分解成2個麥克風子陣列分別優化求解，從而設計出效果更好的波束形成器。

本文提出一種利用Kronecker積將一個大的麥克風陣列分解成2個子陣列，其中一個利用空間差分算子優化求解，另一個則使用零陷約束［12］方法優化求解。最終得到的波束形成器可以進一步在白噪聲增益（white noise gain，WNG）和指向性因子（directivity factor，DF）之間取得平衡，并得到更好的穩健性。

1 信號模型

考慮將均勻線性麥克風陣列作為接收信號的陣列。它由M個全方向性麥克風組成，相鄰2個陣元的間距設為δ，該實驗在遠場模型中進行，即發射信號為平面波。用θ表示方位角，且期望信號方向設為端射方向(θs=0)。

陣列的導向矢量［13-14］為

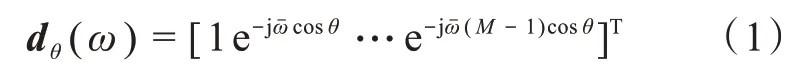
其中，j表示復數的虛部，ωˉ=ωδ/c，ω=2πf表示角頻率，f>0是頻率，c是聲音在空氣中傳播的速度，一般有c=340 m/s。

使用式（1）中定義的方向矢量，頻域內觀察信號的向量表示為：

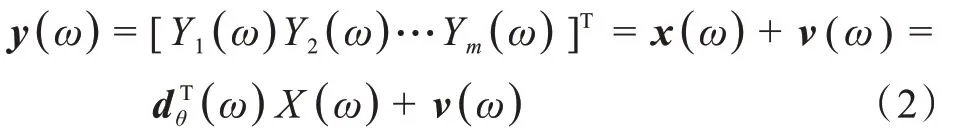
Ym(ω)表示第m（1≤m≤M)個麥克風接收到的信號，X(ω)是零均值期望信號，v(ω)指零均值加性噪聲信號向量，它的數學形式類似于y(ω)。

波束形成通常是指通過對麥克風陣列接收到的觀測信號應用一種空間濾波進行加權的方式，來估測期望信號。一般，波束形成器的輸出可表示為：

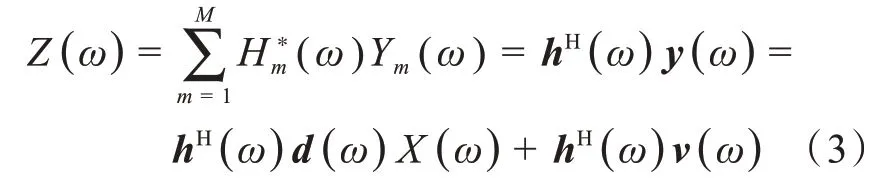
其中，Hm是波束形成器中的第m個元素，Z(ω)是對期望信號X(ω)的估測，上標?表示復共軛。

h(ω)是一個長度為M的線性波束形成器［15-16］。通常，為了獲得無失真的期望信號，需要添加無失真約束：

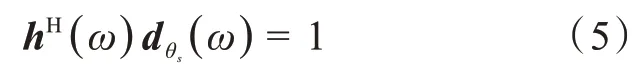
2 測量指標

利用空間差分算子來設計第一個子陣列，對于空間差分算子的定義，可以參考文獻［11］。假設在這里考慮的是一個P（1≤P≤M1）階空間差分陣列。為了簡潔起見，將省略對角頻率ω的表示。

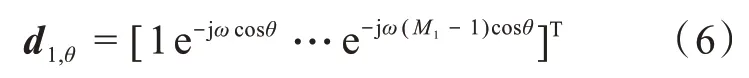
另外有：

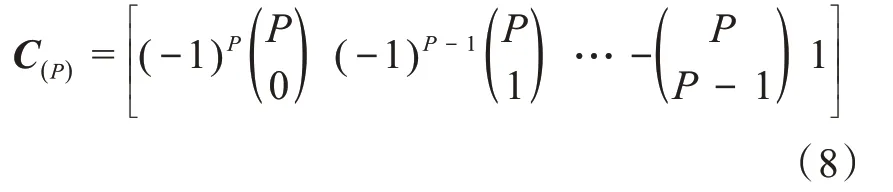
式（8）是一個長度為p+1的向量。，是二項式系數。因此，式（2）在空間差分陣列下的觀測信號為：

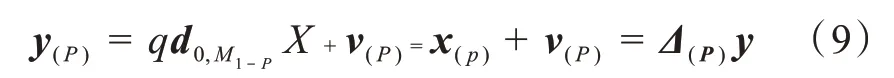
其中，q=τP0

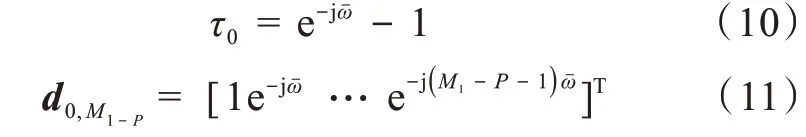
波束形成的過程就是尋找一個空間濾波器對麥克風陣列接收到的期望信號進行強化，對干擾信號和噪聲進行抑制和削弱。因此，一個p階空間差分波束形成，是將一個長度為M1-P的濾波器h(P)作用于觀測信號y(P)。

于是有：

對第二個子陣列，采用零陷約束來設計一個N階差分陣列，其中，N≤M2-1。通常，在使用陣列接收期望信號時，周圍環境中存在的噪聲信號會對其產生干擾，零陷約束的本質是通過在噪聲方向上設置零陷，進而起到抑制噪聲信號，增強期望信號的目的。一般而言，零陷的個數與差分波束形成器的階數數值上相等，假設一個N階差分波束形成器對應的零陷方向分別為θ0;1，θ0;2，…，θ0;N。第二個子陣列的導向矢量為：

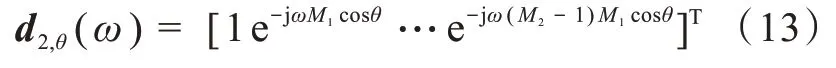
另有：

其中，

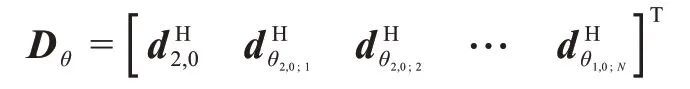
i是(N+1)×(N+1)單位矩陣的第一列。進而：

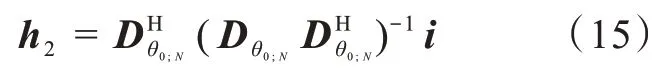
3 Kronecker product方法

利用Kronecker積，將一個由M個麥克風組成的線性陣列分解成2個麥克風子陣列，一個子陣列麥克風數為M1，第二個子陣列麥克風數為M2。其中，M=M1×M2，全局麥克風陣列和第一個子陣列的相鄰兩個陣元間距為δ，第二個子陣列的相鄰2個陣元間距為M1δ，它的結構如圖1所示。而第一個子陣列在利用Kronecker積的過程中可以重復進行運算，因此，只需要M1+M2個麥克風，這樣不僅節約了麥克風成本，而且使麥克風陣列更小巧，便于嵌入到其他設備中。其中，全局導向矢量可以表示為2個子陣導向矢量的Kronecker積，有：

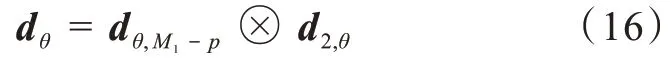
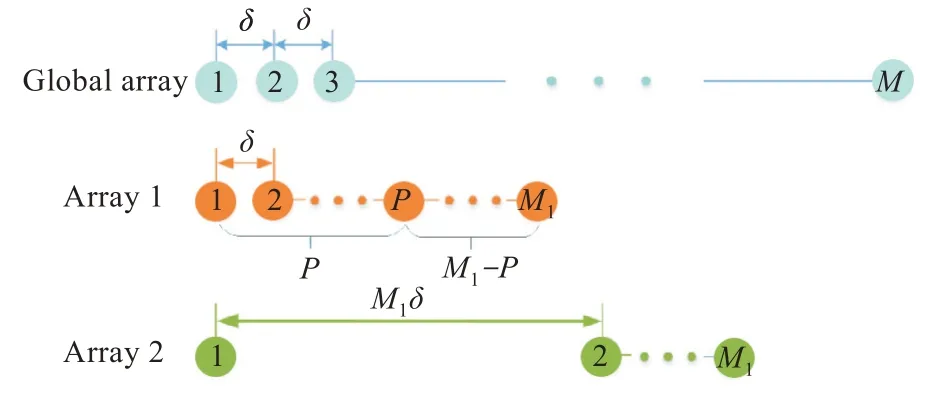
圖1 全局麥克風陣列和麥克風子陣列的模型圖Fig.1 Models of microphone global-array and microphone sub-array

全局波束形成器表示為：

根據Kronecker積的結合律，有：

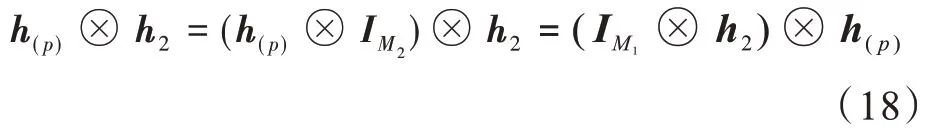
其中IM1和IM2分別表示大小為M1×M1和大小為M2×M2的單位矩陣。

對于設計的波束形成器的好壞進行評判，通常，波束圖（beampattern）、白噪聲增益和指向性因子是波束形成器好壞的衡量指標。

波束圖［17-18］的定義表示為：

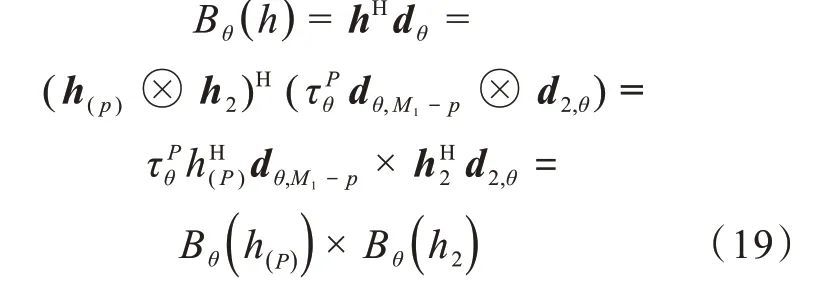
白噪聲增益［19］的定義可表示為：

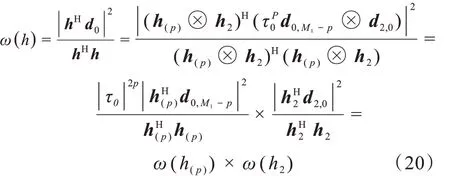
考慮到指向性因子［20-21］是在各向同性噪聲場條件下的測量指標，所以不能單純將2個子陣列的指向性因子相乘。結合式（19），有：

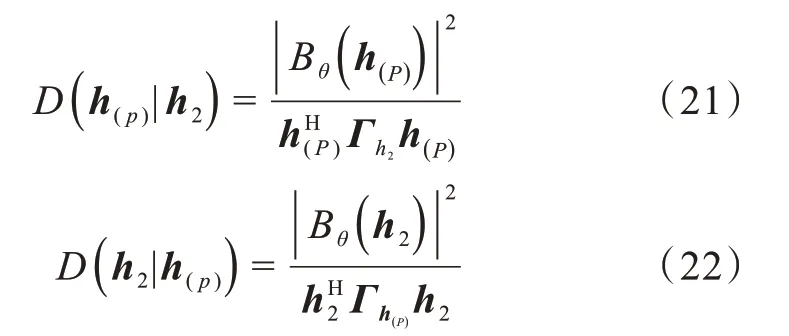
其中，

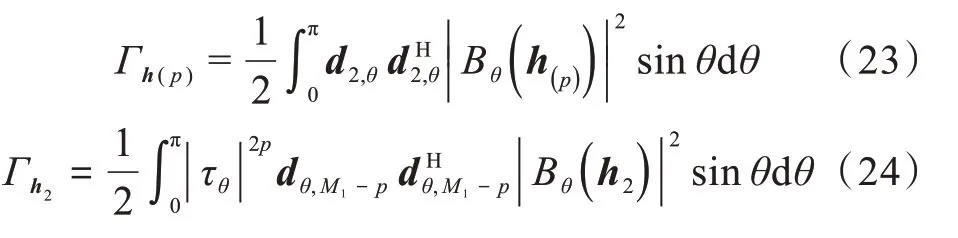
4 仿真實驗

對提出的方法進行仿真實驗，并將其與傳統的方法以及單純的空間差分算子方法進行對比。

使用均勻線性陣列，陣元間距σ=1 cm,期望信號方向為端射方向，即θs=0°。設計傳統差分波束形成的線性陣列的麥克風數M=16，空間差分算子波束形成線性陣列的麥克風數M=4，本文提出的差分波束形成的2個子線性陣列的麥克風數M1=4，M2=4。

圖2顯示了在陣元間距σ=1 cm，頻率f=3 kHz的條件下，圖2（a）為傳統差分波束形成（麥克風數M=16）對應的波束圖、圖2（b）為空間差分算子波束形成（麥克風數M=4）對應的波束圖以及圖2（c）為本文提出的波束形成方法（麥克風數分別為M1=4，M2=4）對應的波束圖，頻率f設為3 000 Hz。圖3畫出了傳統差分波束形成（麥克風數M=16）、空間差分算子波束形成（麥克風數M1=4）和本文提出的波束形成方法（麥克風數M2=4）在陣元間距σ=1cm的條件下，關于頻率f的指向性因子圖3（a）和白噪聲增益曲線圖3（b），其中，D為指向性因子，W為白噪聲增益。通過圖3，可以看到本文提出的方法相比于傳統差分波束形成、空間差分算子波束形成方法，該方法設計的波束形成的指向性因子和白噪聲增益都有一定程度的提升，也就意味著本文提出的方法具有更好的指向性和在白噪聲環境下更高的穩健性。

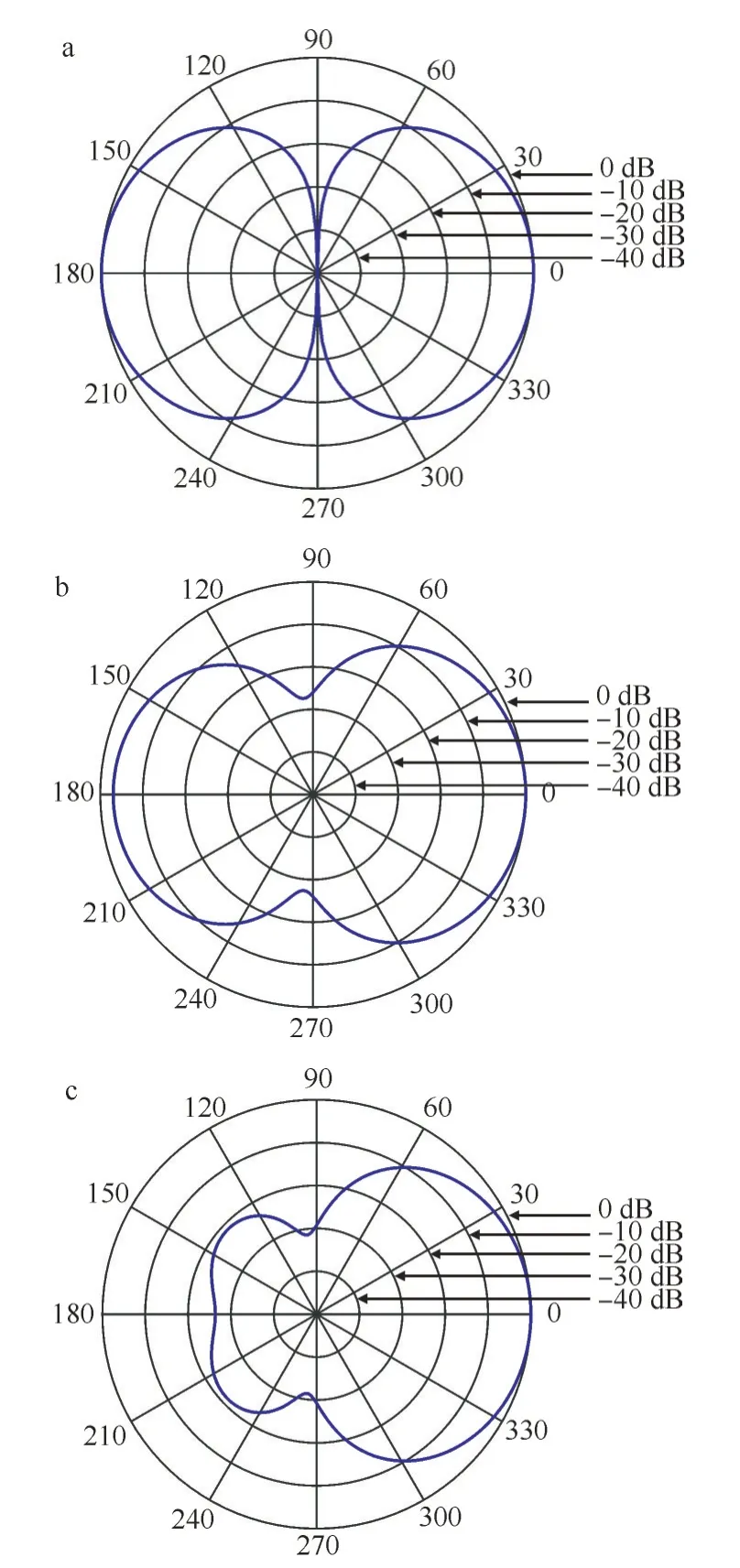
圖2 波束圖比較：（a）傳統差分波束形成，（b）空間差分算子，（c）本文提出的Fig.2 Comparison of beam patterns：（a）tranditional differential beamforming，（b）spatial difference operator，（c）proposed method

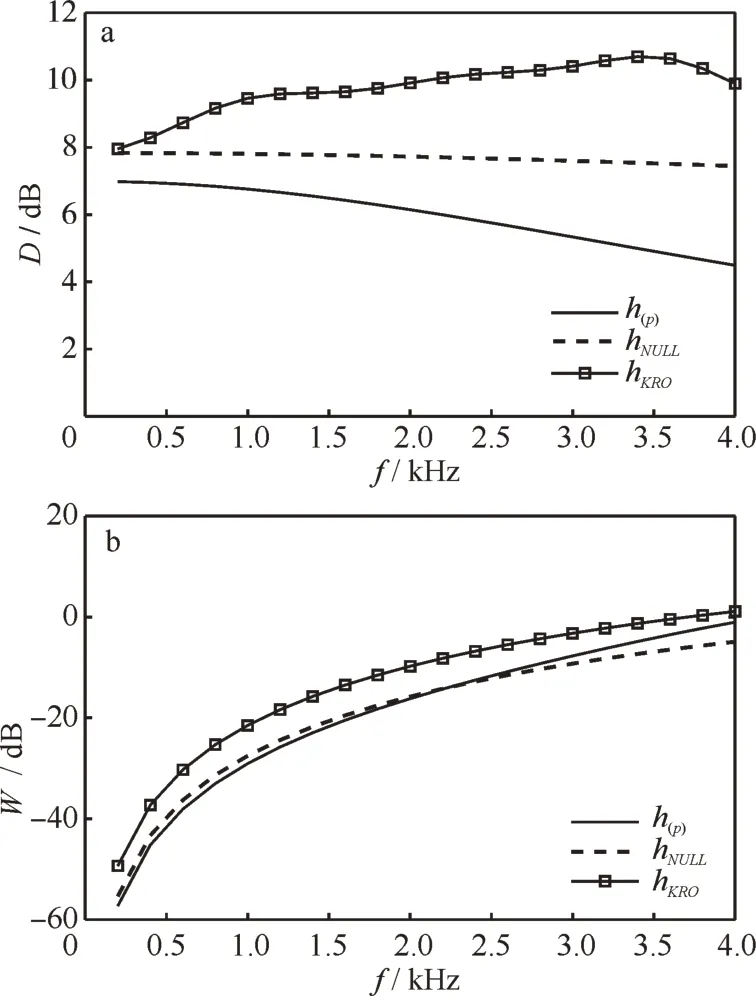
圖3 性能對比：（a）指向性因子（DF），（b）白噪聲增益（WNG）Fig.3 Comparison of performances：（a）directivity factor，（b）white noise gain

5 結論

以上提出通過Kronecker積將一個全局麥克風陣列拆分為2個小的麥克風子陣列來分別優化求解的方法，其中一個子陣列使用零陷約束來求解，另一個子陣列通過空間差分算子算法求解。通過上面的仿真實驗對比，采用Kronecker積的方式設計的波束形成，相比于傳統的波束形成方法以及單純的空間差分算子方法而言，不僅減少了麥克風數量，節約了生產成本。而且，使用Kronecker積來設計的波束形成器具有更高的指向性因子和白噪聲增益，也就意味著設計的波束形成器具有更高的方向指向性和更突出的穩健性。