基于統計建模的VVC快速碼率估計算法

祁偉，殷海兵，王鴻奎，黃曉峰，牛偉宏

基于統計建模的VVC快速碼率估計算法

祁偉，殷海兵，王鴻奎，黃曉峰，牛偉宏

（杭州電子科技大學通信工程學院，浙江 杭州 310018）

為降低新一代通用視頻編碼（versatile video coding，VVC）標準率失真優化過程的編碼復雜度，提出一種基于統計建模的快速碼率估計算法。首先，算法充分考慮依賴性量化（dependent quantization，DQ）的量化行為和熵編碼中的上下文依賴，提出可以準確刻畫編碼過程中上下文狀態遷移的碼率特征，初步預估變換單元（transform unit，TU）中部分語法元素的碼率；其次，基于系數分布特性，定義系數混亂度特征和稀疏度特征來區分系數分布差異帶來的碼率影響，并構建TU級碼率模型；最后，算法根據碼率構成特性將大尺寸TU和小尺寸TU分開建模實現更精準的碼率預估。通過統計方式對大量樣本進行回歸訓練，得到最終的線性碼率模型，并應用于VVC的模式決策中。實驗結果表明，所提出算法在隨機訪問（random access，RA）配置下，可以實現16.289%的復雜度降低，而碼率變化率（Bjontegaard delta bit rate，BD-BR）僅增加1.567%。

碼率預估；通用視頻編碼；率失真優化；回歸訓練

0 引言

為滿足不斷增長的視頻壓縮需求，JVET（Joint Video Exploration Team）提出新一代通用視頻編碼[1]，其中采用諸多新的編碼技術，如多種劃分模式、多變換核選擇、改進的熵編碼[2]和依賴性量化[3]等。相比上一代高效視頻編碼（high efficiency video coding，HEVC）[4]，VVC以復雜度增加為代價，提高約50%的視頻編碼效率。

在VVC中模式決策過程基于率失真優化（rate distortion optimization，RDO）[5]技術實現。盡管豐富的多模式預測和自適應DQ技術的使用極大提升了編碼性能，但是大量的候選模式通過預測、變換、量化和熵編碼過程獲取碼率代價，這加劇了率失真優化過程的計算復雜度和串行依賴，為視頻編碼標準的實際應用帶來困難。

因此一些學者針對率失真優化過程中的碼率計算復雜度問題展開研究。在H.264/AVC[6]中，Sarwer等[7]基于上下文自適應變長編碼（context adaptive variable length coding，CAVLC）特性，使用變換塊系數絕對值之和、高頻區域非零系數位置和非零系數數量來預估對應殘差塊碼率；Zhao等[8]基于零均值廣義高斯分布模型，使用量化系數加權和來預測變換塊碼率；Tu等[9]簡化RDO流程，使用變換域中非零系數數量與變換系數和來預估變換塊碼率。在H.265/HEVC中，一些學者[10-12]從信息熵角度出發，統計各語法元素的二元結果，計算0和1符號的信息熵，以此來預估系數碼率；Hu等[13]和Huang等[14]從硬件友好的角度出發，使用變換系數和位置信息進行快速的系數碼率預估；Sheng等[15]基于上下文自適應二進制算術編碼（context-based adaptive binary arithmetic coding，CABAC）特性，使用量化系數幅度和位置特征來預估系數塊碼率；Liu等[16]根據上下文分類特性對系數組（coefficient group，CG）進行二元分類，并使用6個系數分布特征預估部分語法元素碼率；Sun等[17]在變換域建立閾值區分變換系數是否量化為0，并使用變換系數幅值和位置信息預估碼率；孟翔等[18]對不同位置的量化系數進行自適應加權，并結合位置特征，實現較為準確的變換塊碼率預估。然而已有算法均是在H.264和H.265平臺上實現的，而VVC使用多種劃分方式和改進的熵編碼等，導致現有算法很難深入描述VVC中上下文更新時影響碼率變化的根本因素，因此進行系統精確的碼率建模仍面臨挑戰。

針對以上問題，本文提出一種基于統計建模的VVC快速碼率估計算法減少模式決策復雜度。首先，本文基于DQ量化行為和熵編碼特性提出可以準確刻畫編碼過程中上下文狀態遷移的碼率特征，初步估計部分語法元素碼率；其次，本文從系數分布特性出發，提出系數混亂度特征和稀疏度特征來減小預測誤差，并構建整個變換單元（transform unit，TU）級碼率模型；最后，根據碼率構成特性，將TU分為大尺寸和小尺寸建模處理，可以更準確地預估碼率。

1 語法元素編碼結構

在模式決策過程中，VVC通過拉格朗日公式進行率失真代價的計算：

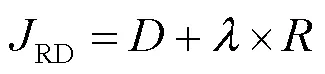
第1次系數掃描編碼時，有效系數標志（significant coefficient flag，SCF）表示當前系數是否非零，系數大于1標志（greater than 1，GT1）表示系數絕對值是否大于1，奇偶校驗標志（parity，PAR）表示系數絕對值減去2后的奇偶性，系數大于3（greater than 3，GT3）標志表示當前系數絕對值是否大于3。第2次系數掃描時，剩余（remaining，REM）系數標志表示系數絕對值減去4的剩余部分。VVC對第1次掃描中已經編碼的上下文比特數量有所限制[2]，如果在掃描位置開始時，變換塊中SCF、GT1、PAR和GT3編碼的比特總數超過一定值，則在此處終止第1次和第2次系數掃描，剩余掃描位置的系數絕對值||在第3次掃描過程中進行旁路編碼，由語法元素剩余系數絕對值標志（dec-abs-level，DEC）表示。在第4次系數掃描時，系數符號標志（coefficient sign flag，CSF）表示當前系數是否為正。VVC語法元素掃描編碼圖如圖1所示，其中閃電標志表示在此處終止第1次和第2次系數掃描。

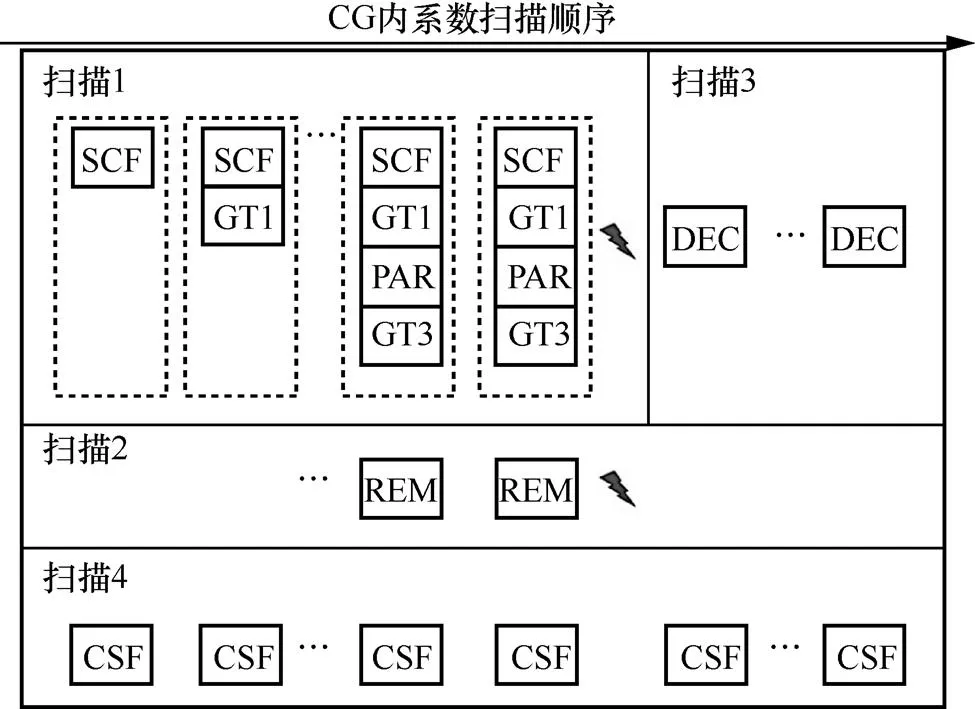
圖1 VVC語法元素掃描編碼圖

在DQ選擇最優量化索引的率失真優化過程和熵編碼過程中，會對語法元素進行復雜的上下文建模和概率狀態更新，這會帶來極大的上下文依賴。此外DQ量化技術基于維特比搜索算法進行最優量化路徑的選擇，這樣可以實現更好的比特節省，但是其計算復雜度更高且不利于硬件并行化處理。因此如何避免復雜的DQ量化和上下文更新進行系統準確的碼率建模對于快速的碼率估計算法是非常關鍵的。

2 量化系數碼率模型

首先本文使用相對簡單的硬決策量化（hard decision quantization，HDQ）[19]代替復雜度較高的DQ量化方式。其次，為了準確預估量化系數比特，本文基于DQ量化行為和熵編碼中的語法元素上下文分類原則開發整體碼率特征，并驗證和使用能夠表示系數分布特性的混亂度和稀疏度特征，共同開發了TU級碼率模型。最后在建模過程中發現VVC中存在小于16個系數[2]的TU，即2×2、2×4、4×2尺寸的TU，這些小尺寸TU和大尺寸TU的碼率構成相差很大，因此本文將它們分開進行碼率建模。

2.1 大尺寸TU上下文特征

在現有碼率估計算法中，Liu等[16]根據上下文分類原則對系數組進行二元分類，并使用6個系數分布特征預估CG內語法元素SCF、GT1和GT3的碼率。該算法在H.265平臺上可以較為準確地預估系數塊碼率，但是VVC中上下文轉換原則發生改變[2]，使得其碼率特征很難深入刻畫上下文狀態轉換時碼率變化的根本因素。VVC局部鄰域模板圖和頻區分布圖如圖2所示。圖2（a）為VVC從當前量化系數與鄰近系數之間的依賴關系出發提出的局部鄰域模板，其中黑色方塊表示待編碼系數，灰色方塊表示其局部鄰域系數。根據局部統計特性[20]，語法元素SCF、PAR、GT1和GT2的上下文概率模型受多種因素影響，包括有當前系數位置、局部鄰域系數的部分重建值之和、局部鄰域中非零系數數量和DQ狀態。局部鄰域系數部分重建值之和表示如下。

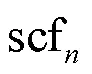
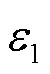
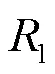
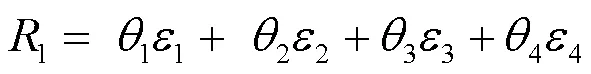
2.2 位置參數和系數分布特征

圖3 TU級別R1與真實碼率之間的關系

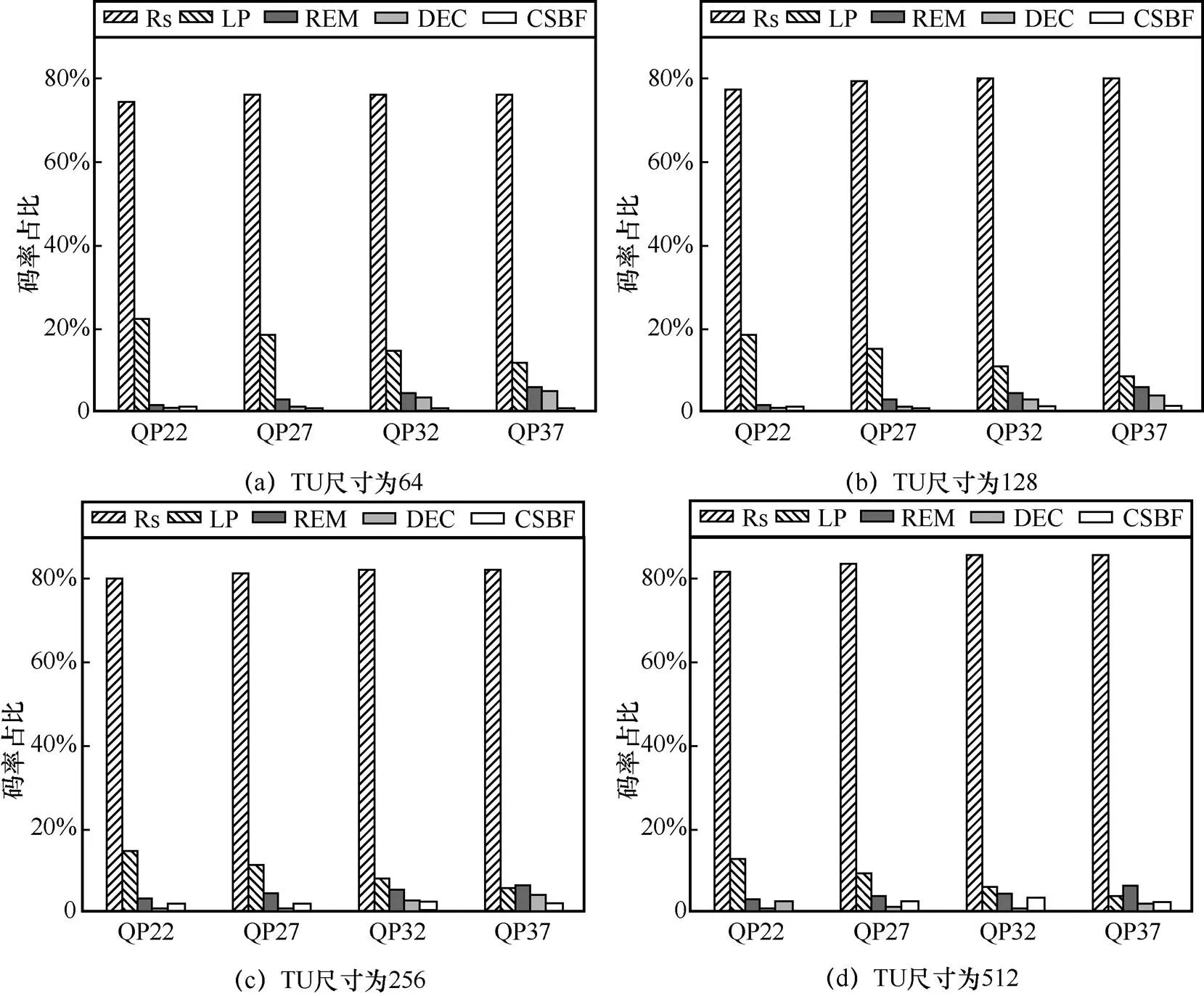
圖4 不同TU尺寸和不同QP下語法元素的碼率占比結果

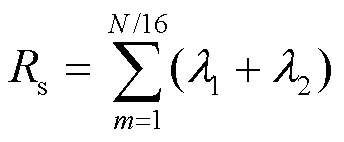
其中，表示變換單元的尺寸。當QP為37時，系數分布特征與真實碼率之間的關系如圖5所示。

2.3 大尺寸TU最終碼率模型

經過上述分析，大尺寸TU最終碼率模型如下。

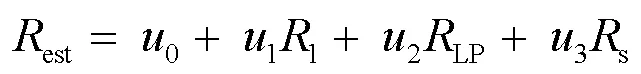
圖5 系數分布特征與真實碼率之間的關系

2.4 小尺寸TU最終碼率模型

由于小尺寸TU系數較少，處于不同掃描位置的系數對碼率代價造成的影響區別較大，因此本文使用加權量化系數[18]的方法來描述位置信息對碼率代價的不均勻貢獻，并使用全局混亂度特征減小預估碼率與真實碼率間的誤差。最終模型如下。

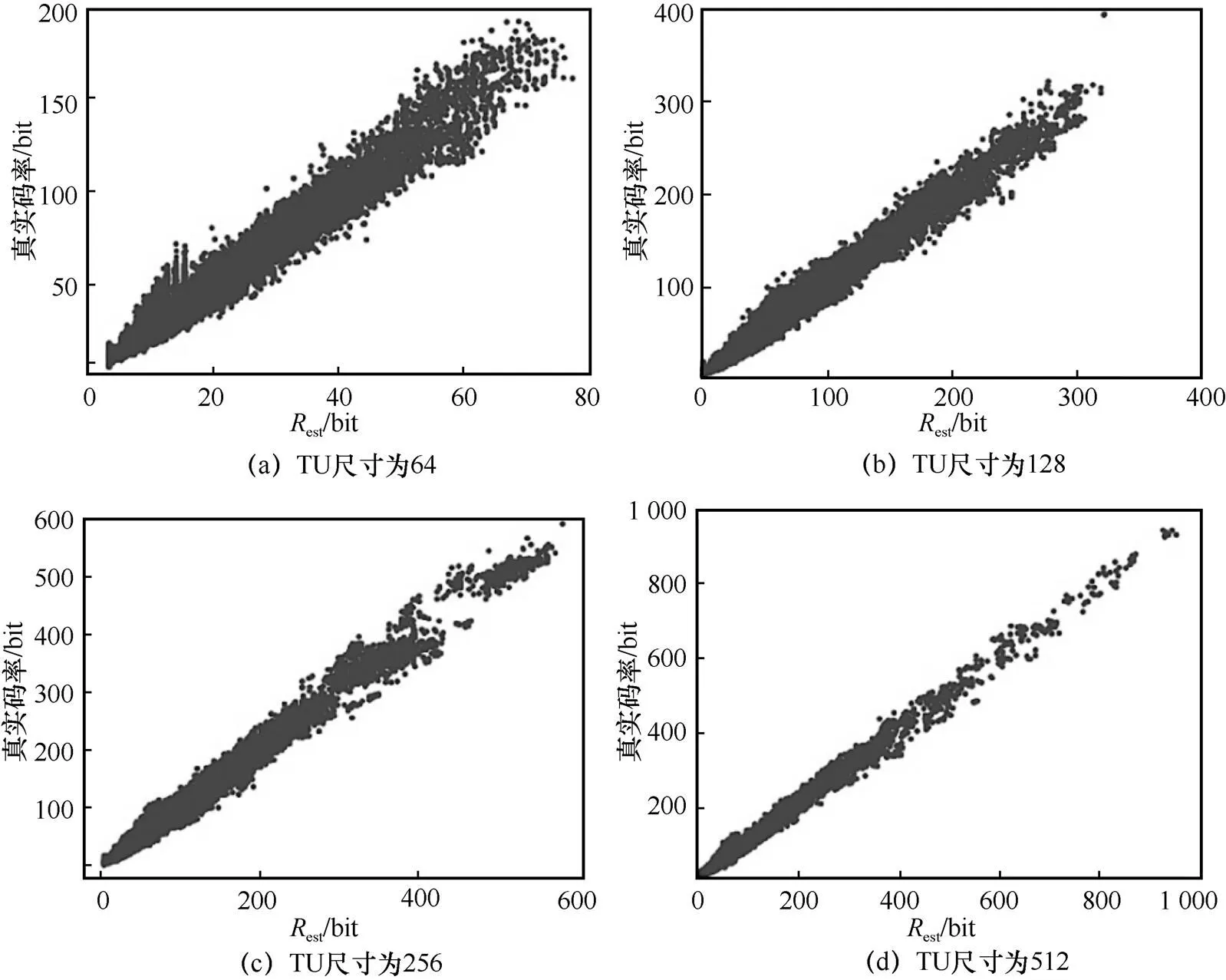
圖6 大尺寸TU預估碼率與真實碼率之間的關系

圖7 小尺寸TU預估碼率與真實碼率之間的關系

3 實驗結果分析

首先為評估第2節提出的碼率模型精度，本文對不同情況下預估碼率和真實碼率的誤差進行統計，并對不同區間誤差的概率進行歸一化處理，碼率誤差的歸一化概率如圖8所示。其中，方形符號、三角符號和圓點分別表示文獻[17]、文獻[18]和本文提出的碼率預估算法的誤差歸一化概率圖，需要說明的是，編碼塊預估碼率會在真實碼率附近浮動，當預估碼率小于真實碼率時，對應預測誤差為負值。測試序列為紋理細節較多的BasketballDrillText。可以看出，Sun等[17]提出的算法由于特征相對較少，對碼率變化的深層原因描述不夠精準，導致模型精度不夠穩定，誤差相對較大。而孟翔等[18]提出的模型由于VVC中上下文分類原則轉變導致其算法適用性不強，模型精度相對較低。因此本文提出的碼率預估算法相對更加準確，預估誤差也更小。

圖8 碼率誤差的歸一化概率

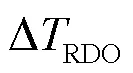
在Sun等[17]的算法中，將TU中變換系數幅度，非零系數位置和最后一位非零系數位置作為特征進行碼率建模。由于算法碼率特征較少，很難深入描述上下文更新時碼率變化的根本因素，在VVC中造成較大的性能損失。具體地說，對于一些高分辨率視頻序列，如Tango2、Campfire和ParkRunning3，Sun等[17]的算法BD-BR分別上升1.83%、1.92%、1.65%，而本文算法在這些序列的BD-BR分別上升1.52%、1.75%、1.25%。同時對于一些低分辨率視頻序列，如BasketballPass、RaceHorses和BasketballDrillText，Sun等[17]的性能損失分別為2.06%、2.46%、2.59%，本文算法在這些序列的性能損失分別為1.10%、1.44%、1.57%。這說明對于不同分辨率的視頻序列，本文算法皆比Sun等[17]的算法實現更好的編碼效率。而在時間復雜度方面，對于高分辨率視頻序列，如Tango2和Campfire，時間節省分別為20.34%和17.65%，最大值和最小值相差2.69%，而本文在高分辨率對應視頻序列時間節省分別為21.36%和19.86%，最大值和最小值相差僅1.5%。同時對于低分辨率視頻序列如BasketballDrillText和SlideShow，時間節省分別為12.32%和8.14%，兩者相差4.18%，而本文算法中對應低分辨率視頻序列時間節省分別為11.03%和8.67%，兩者相差僅2.46%。這說明對于不同分辨率的視頻序列，而本文算法相比Sun等[17]的算法時間節省更加均勻，算法適用性更好。

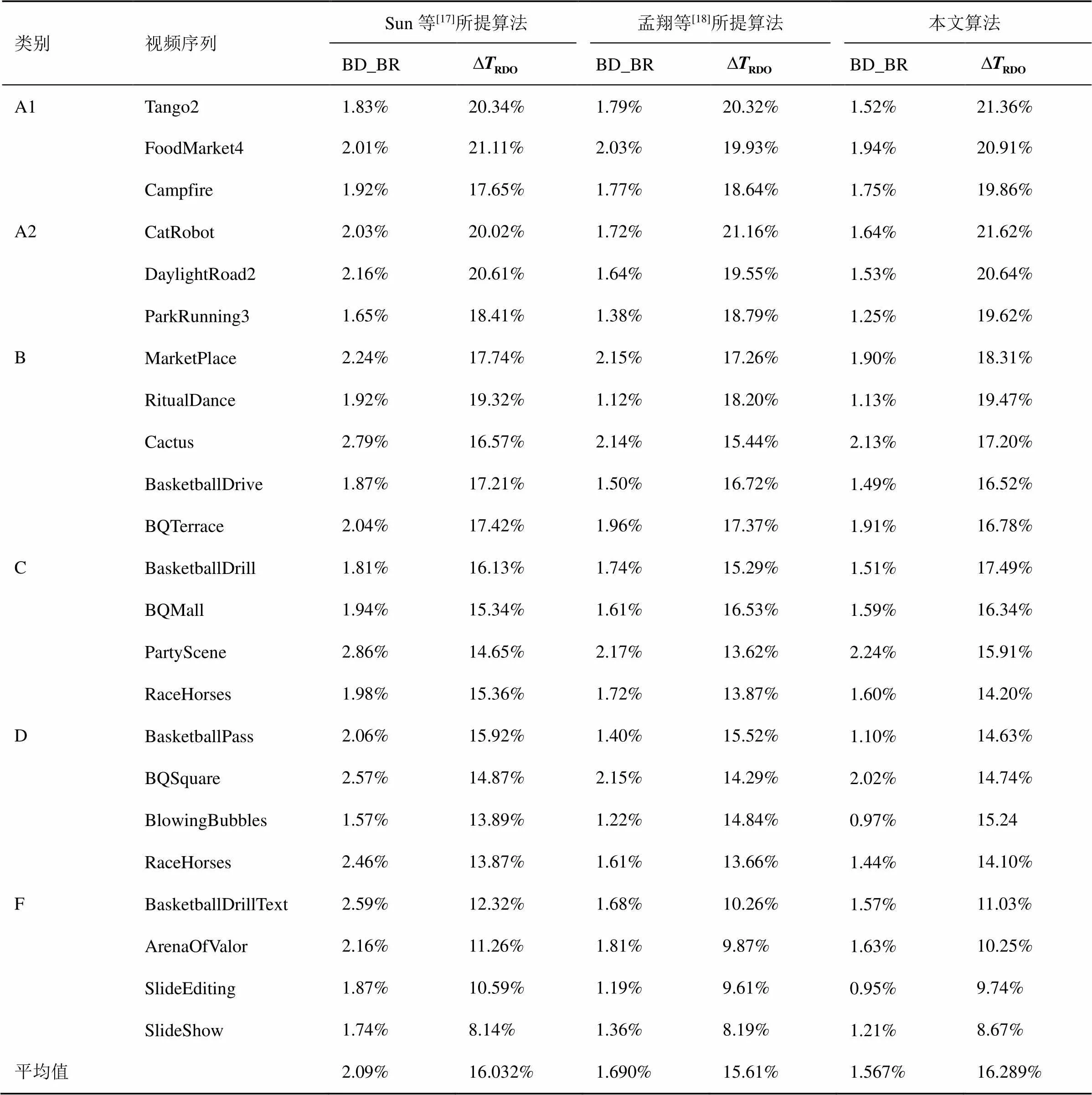
表1 在Random Access下模型性能

在孟翔等[18]所提算法中，對位于不同位置的量化系數進行自適應加權，并根據上下文分類依據對CG進行分組，在HEVC中可以實現相對準確的碼率預估。但是VVC中劃分模式的增加和上下文選取原則的改變[2]使得文獻[15]的算法在VVC中的效果并不突出。具體地說，對于一些紋理細節較多的視頻序列，如FoodMarket4、BQSquare和BasketballDrillText，其BD-BR分別上升2.03%、2.15%、1.68%，而在本文的算法中其性能分別提升0.09%、0.13%、0.11%。對于背景較為均勻的視頻序列，如RitualDance、BlowingBubbles和SlideEditing，其BD-BR分別上升1.12%、1.22%、1.19%，在本文的算法中其性能分別提升0.01%、0.25%、0.24%。因此對于紋理細節不同的視頻序列來說，本文從上下文選取原則角度出發建立的TU級碼率模型相較于孟翔等[18]的算法可以實現更加準確的碼率預估，性能損失更小。而在時間復雜度方面，孟翔等[18]的算法碼率模型參數較多，因此RDO節省時間較少。具體地說，對于紋理細節較多的視頻序列，如FoodMarket4和BasketballDrillText，時間節省分別為19.93%和10.26%，而本文算法對應時間節省為20.91%和11.03%。而對于背景較為均勻的視頻序列，如RitualDance和BlowingBubbles，時間節省分別為18.2%和14.84%，而本文對應時間節省為19.47%和15.24%。可以看出無論是在紋理細節較多還是背景相對均勻的視頻序列中，本文算法相比于孟翔等[18]所提算法可以實現更大的時間節省。

4 結束語

本文針對VVC率失真優化過程中復雜的碼率計算問題，提出一種基于統計建模的快速碼率估計算法。算法首先充分考慮依賴性量化的量化行為和熵編碼中的上下文依賴，提出一種準確預估部分語法元素碼率的初步模型；然后提出混亂度和稀疏度特征描述系數整體分布對碼率的影響，并進一步形成TU級碼率模型；最后根據碼率構成特性，算法將大尺寸TU和小尺寸TU分開建模實現更精準的碼率預估。實驗結果表明，在RA配置下，提出方案在性能基本不變的情況下節省16.289%的率失真優化時間。

[1] BROSS B, WANG Y K, YE Y, et al. Overview of the versatile video coding (VVC) standard and its applications[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2021, 31(10): 3736-3764.

[2] SCHWARZ H, COBAN M, KARCZEWICZ M, et al. Quantization and entropy coding in the versatile video coding (VVC) standard[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2021, 31(10): 3891-3906.

[3] SCHWARZ H, NGUYEN T, MARPE D, et al. Hybrid video coding with trellis-coded quantization[C]//Proceedings of 2019 Data Compression Conference (DCC). Piscataway: IEEE Press, 2019: 182-191.

[4] SULLIVAN G J, OHM J R, HAN W J, et al. Overview of the high efficiency video coding (HEVC) standard[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2012, 22(12): 1649-1668.

[5] SULLIVAN G J, WIEGAND T. Rate-distortion optimization for video compression[J]. IEEE Signal Processing Magazine, 1998, 15(6): 74-90.

[6] WIEGAND T, SULLIVAN G J, BJONTEGAARD G, et al. Overview of the H.264/AVC video coding standard[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2003, 13(7):560-576.

[7] SARWER M G, PO L M. Fast bit rate estimation for mode decision of H.264/AVC[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2007, 17(10): 1402-1407.

[8] ZHAO X, SUN J, MA S W, et al. Novel statistical modeling, analysis and implementation of rate-distortion estimation for H.264/AVC coders[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2010, 20(5): 647-660.

[9] TU Y K, YANG J F, SUN M T. Efficient rate-distortion estimation for H.264/AVC coders[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2006, 16(5):600-611.

[10] CHEN W G, WANG X. Fast entropy-based CABAC rate estimation for mode decision in HEVC[J]. SpringerPlus, 2016, 5(1): 1-10.

[11] CHEN H C, CHANG T S. Fast rate distortion optimization with adaptive context group modeling for HEVC[C]//Proceedings of 2017 IEEE International Symposium on Circuits and Systems. Piscataway: IEEE Press, 2017: 1-4.

[12] SHARABAYKO M P, PONOMAREV O G. Fast rate estimation for RDO mode decision in HEVC[J]. Entropy, 2014, 16(12): 6667-6685.

[13] HU L D, SUN H M, ZHOU D J, et al. Hardware-oriented rate-distortion optimization algorithm for HEVC intra-frame encoder[C]//Proceedings of 2015 IEEE International Conference on Multimedia & Expo Workshops. Piscataway: IEEE Press, 2015: 1-6.

[14] HUANG X F, JIA H Z, CAI B B, et al. Fast algorithms and VLSI architecture design for HEVC intra-mode decision[J]. Journal of Real-Time Image Processing, 2016, 12(2): 285-302.

[15] SHENG Z, ZHOU D, SUN H, et al. Low-complexity rate-distortion optimization algorithms for HEVC intra prediction[C]//Proceedings of International Conference on Multimedia Modeling. Cham: Springer, 2014: 541-552.

[16] LIU Z Y, GUO S C, WANG D S. Binary classification based linear rate estimation model for HEVC RDO[C]//Proceedings of 2014 IEEE International Conference on Image Processing. Piscataway: IEEE Press, 2014: 3676-3680.

[17] SUN H M, ZHOU D J, HU L D, et al. Fast algorithm and VLSI architecture of rate distortion optimization in H.265/HEVC[J]. IEEE Transactions on Multimedia, 2017, 19(11): 2375-2390.

[18] 孟翔, 殷海兵, 黃曉峰. 基于統計建模的HEVC快速率失真估計算法[J]. 電信科學, 2021, 37(1): 58-68.

MENG X, YIN H B, HUANG X F. Statistical modeling based fast rate distortion estimation algorithm for HEVC[J]. Telecommunications Science, 2021, 37(1): 58-68.

[19] SCHWARZ H, NGUYEN T, MARPE D, et al. Hybrid video coding with trellis-coded quantization[C]//Proceedings of 2019 Data Compression Conference (DCC). Piscataway: IEEE Press, 2019: 182-191.

[20] SCHWARZ H, NGUYEN T, MARPE D, et al. Improved quantization and transform coefficient coding for the emerging versatile video coding (VVC) standard[C]//Proceedings of 2019 IEEE International Conference on Image Processing. Piscataway: IEEE Press, 2019: 1183-1187.

[21] BOSSEN F, BOYCE J, LI X, et al. JVET common test conditions and software reference configurations for SDR video[EB]. 2019.

[22] BJONTEGAARD G. Calculation of average PSNR differences between RD-curves [EB]. 2001.

Statistical modeling based fast rate estimation algorithm for VVC

QI Wei, YIN Haibing, WANG Hongkui, HUANG Xiaofeng, NIU Weihong

College of Communication Engineering, Hangzhou Dianzi University, Hangzhou 310018, China

To reduce the coding complexity of the rate-distortion optimization process of the latest video coding standard versatile video coding (VVC), a fast rate estimation model based on statistical modeling was proposed. Firstly, the quantization behavior in dependent quantization (DQ) and the context dependency in entropy coding were fully considered. Features that could describe context state transition in the coding process were proposed to estimate rate of some synatax elements in a TU preliminarily. Secondly, coefficient chaos and sparsity features were proposed to distinguish the influence of coefficient distribution difference on the rate cost based on the coefficient distribution characteristics which built a TU level rate model. Finally, large-size transform unit (TU) and small-size TU was modeling respectively according to the rate composition character to achieve more accurate rate estimation. A large number of parameters were trained by regression model through statistical methods, and the final linear rate model was obtained which was applied to the mode decision. Experimental results show that the proposed algorithm can achieve 16.289% complexity reduction with 1.567% BD-BR increase for RA configuration.

rate estimation, VVC, RDO, regression training

TN919.81

A

10.11959/j.issn.1000–0801.2022279

2022–05–13；

2022–10–20

殷海兵，yhb@hdu.edu.cn

國家自然科學基金資助項目（No.61972123，No.62031009）；浙江省尖兵研發攻關計劃項目（No.2022C01068）

祁偉（1995– ），男，杭州電子科技大學碩士生，主要研究方向為視頻編解碼。

殷海兵（1974– ），男，博士，杭州電子科技大學教授，主要研究方向為數字視頻編解碼。

王鴻奎（1990– ），男，博士，杭州電子科技大學講師，主要研究方向為感知視頻編碼。

黃曉峰（1988– ），男，博士，杭州電子科技大學教授，主要研究方向為感知視頻編碼。

牛偉宏（1998– ），男，杭州電子科技大學碩士生，主要研究方向為視頻編解碼。

s: The National Natural Science Foundation of China (No.61972123, No.62031009), Zhejiang Provincial Pioneer Research and Development Project (No.2022C01068)