易逝品在線銷售數據的稀疏性問題及處理

吳宇平 李 磊

（新疆財經大學統計與數據科學學院，新疆 烏魯木齊 830000）

一、引言

隨著互聯網和大數據技術的高速發展，數據量迅猛增長，數據形式越來越多樣化。其中，稀疏數據這一特殊形式的數據成為研究者越來越關注的話題。稀疏數據絕對不是無用的數據，只是信息不完全的數據，通過適當的技術方法，可以從中挖掘出所需的有效信息[1]。

稀疏數據廣泛存在于各種應用場景中。應用場景不同，稀疏數據表現出的特點不同，適用的稀疏性處理方法也不同。根據數據表現出的特點，可將稀疏數據分為三種類型：

第一種類型的稀疏數據指由于某些原因導致其中一部分數據值缺失的數據，也稱為缺失數據[2]。例如，在數據收集的過程中，采用不恰當的觀測手段或錄入數據時發生錯誤，導致在問卷調查、醫學研究、社會經濟研究及其他科學研究中經常會出現數據缺失的現象，使信息被遺漏。Tutz 和Ramzan（2015）[3]針對高維的缺失數據，提出了基于距離的加權最近鄰插補法。針對缺失數據較多的情況，Silv 和Perera（2016）[4]提出了進化KNN 插補法。Galan 和Lasheras 等（2017）[5]基于遺傳算法，提出適用于測試和問卷的缺失數據處理方法。

第二種類型的稀疏數據指數據本身不存在缺失，但可利用的有效數據不足[6]。例如，在亞馬遜或YouTube的推薦系統中，產品數量非常龐大，但網站上較活躍的用戶群只對其中不到1%的產品有過消費記錄，所以推薦系統可利用的消費記錄數據非常稀少。數據的稀疏性問題會對推薦結果的準確性產生影響。對此，王喜智[6]提出了結合巴氏距離與雅克比距離的稀疏數據用戶相似度模型，以提高推薦質量。在商品的最優定價研究中，針對歷史銷售數據中可利用的有效數據點較少的問題，Bauer 和Jannach（2018）[7]采用BootStrap 和核回歸相結合的稀疏性處理方法來估計一個價格點是否是最優的概率。

第三種類型的稀疏數據指具有稀疏分布特性的數據，即數據的分布是稀疏的。例如，大氣腐蝕數據的分布是嚴重稀疏的，其絕大部分數據集中在ISO 9223：1992（E）中少數等級上，數據分布嚴重不均，李志平和付冬梅等（2016）[8]針對大氣腐蝕等級數據的稀疏分布特性，提出了一種基于稀疏數據歸約的CMAC大氣腐蝕數據補償方法。李穩和劉伊克等（2016）[9]針對井下微震監測數據的稀疏分布特征，提出將圖像處理領域適宜稀疏分布信號降噪處理的稀疏碼收縮方法應用于井下微震監測數據處理。時空數據的稀疏分布是當前大數據挖掘面臨的普遍問題，程詩奮和彭澎等（2020）[10]針對地理時空數據的稀疏分布特性，提出了時空數據重構解決方案。

在電子商務領域，受季節、特殊節日、需求不確定性以及商品自身特性等多種因素的影響，收集到的易逝品在線銷售數據常常具有稀疏性，給易逝品的定價研究帶來一定困難。為了從易逝品在線銷售數據中挖掘出關于最優價格的有效信息，為易逝品定價提供決策支持，本文圍繞易逝品在線銷售數據的稀疏性問題展開研究，根據易逝品在線銷售數據表現出的稀疏性特點，將適宜于此類稀疏性問題處理的BootStrap 和核回歸相結合的方法應用于易逝品在線銷售數據處理。

二、易逝品在線銷售數據的稀疏性問題

為展現易逝品在線銷售數據的稀疏性，本文選用李磊和宋建偉（2020）[11]使用的數據集中的部分數據，并對其進行描述性統計分析。該數據集是大棗、葡萄干、巴旦木3 種新疆特色農產品的相關數據，主要通過Python 網絡爬蟲程序和人工抓取相結合的方法從淘寶和天貓平臺獲得。從2018年4月6日到2018年10月27日，每3 天收集一次數據，共69 個觀測時點。

本文選取規格為500g 的大棗作為研究對象。首先，選取該規格大棗的觀測時間、銷售價格和銷售量3個變量；其次，用銷售價格乘以相應的銷售量得到銷售收入，由于數據集中各銷售量觀測值指的是近30 天的銷量，故這里計算得到的各銷售收入值也是近30 天的收入；最后，將該易逝品的銷售價格、觀測時間（即銷售價格保持不變的時長）、銷售量、銷售收入4個變量對應的共2546 條數據作為本文的數據集，該數據集中各變量的描述性統計見表1。

表1 數據的描述性統計

由表1可知，銷售價格在11.80—49.90 元之間變動；銷售價格保持不變的時長在9.00—204.00 天之間變動，銷售價格保持不變的平均時長為85.92 天，中位數為85.50 天，其平均值和中位數均接近3 個月。

圖1是各銷售價格保持不變的時長的頻數分布直方圖，橫坐標表示銷售價格保持不變的時長，縱坐標表示頻數，可以看出，各銷售價格保持不變的時長長短不一，最長的時長達到了204 天。由于易逝品的價值會隨時間的增加逐漸減少，從而導致消費者的購買欲望下降，因此易逝品銷售價格的變動相較于其他商品理應更為頻繁，即隨著時間的增加，商家可適當調整銷售價格，以適應不斷變化的市場需求，實現利潤最大化。但從表1和圖1可以看出，本文研究所選取的易逝品的在線銷售數據具有價格長時間保持不變的特點，即價格變動并不頻繁。若要對某商家的商品進行動態定價研究，可利用的價格數據點較少，該特點與第二種類型稀疏數據的特點一致。

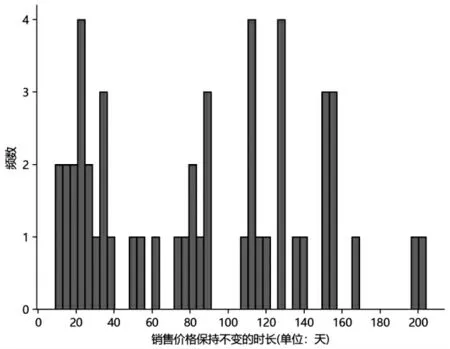
圖1 銷售價格保持不變的時長的頻數分布直方圖

圖2是銷售價格-平均銷售收入散點圖，橫坐標表示銷售價格，縱坐標表示平均銷售收入，銷售價格對應的平均銷售收入指該價格保持不變的時長內，所觀測到的銷售收入的平均值。圖中水平虛線代表所有銷售價格對應的平均銷售收入的均值，從圖中可以看出：大部分的點分布在虛線附近，平均銷售收入隨銷售價格變化的趨勢和規律并不明顯。表現銷售價格如何影響平均銷售收入的有效數據點較少，該特點與第二種類型稀疏數據的特點一致。

從圖2還可以看出，區間（10，20）內有16 個價格點、區間（20，30）內有18 個價格點、區間（30，40）內有13 個價格點，而區間（40，50）內只有3 個價格點。（10，20）、（20，30）、（30，40）3 個區間內的價格點數量較為接近，均在10 以上，而（40，50）內的價格點數量與前3 個區間相比差距較大，且區間（10，20）、（20，30）、（30，40）內的點較密集，而區間（40，50）內的點非常稀疏。參考李志平和付冬梅等（2016）[8]的研究，在區間大小相同的情況下，各區間內的數據點數量相差大，且分布不均，稀疏密度差距大，說明數據是稀疏分布的，故本文研究所選取的價格數據是稀疏分布的，該特點與第三種類型稀疏數據的特點一致。

圖2 銷售價格-平均銷售收入散點圖

三、易逝品在線銷售數據的稀疏性處理方法

針對易逝品在線銷售數據表現出的稀疏性特點，本文采用BootStrap 和核回歸相結合的方法處理易逝品在線銷售數據的稀疏性問題。首先，運用BootStrap方法計算各離散價格點對應的BootStrap 置信度；其次，運用核回歸方法對離散價格點的BootStrap 置信度進行擬合，從而得到整個定價區間上連續價格水平與其對應的BootStrap 置信度之間的非線性函數關系。由于每個價格水平對應的BootStrap 置信度可作為該價格水平是最優價格的概率估計，故對易逝品在線銷售數據進行稀疏性處理后，可初步得到定價區間內任意價格水平是最優價格的概率估計值。

（一）離散價格點的BootStrap 置信度計算

BootStrap 方法是統計學中一種重要的非參數估計方法，該方法在數據分析方面有著廣泛應用。BootStrap方法的基本思想是在原始數據基礎上進行有放回抽樣，從而產生一系列樣本量相同的BootStrap 樣本，并利用這些樣本對總體進行推斷。當數據分布未知或樣本容量較小時，BootStrap 方法仍然是有效的。BootStrap方法的具體步驟為：假設一個數據樣本的總體分布F未知，但已知有一個來自分布F 的數據樣本D，其樣本容量為N，從該樣本中進行有放回的抽樣，抽取后樣本容量仍為N。相繼獨立地從原始樣本中抽取多個BootStrap 樣本，然后利用這些樣本對整體進行統計推斷[12]。

假設真實觀測到的售價集合為{pn｜n=1，2，…，N}，Hn表示真實銷售價格pn保持不變的時長；Rn1，Rn2，…，Rnk表示在時長Hn內，售價pn所對應的k 個真實觀測到的日銷售收入；Rn=（Rn1+Rn2+…+Rnk）/k 表示在時長Hn內，售價pn對應的日平均銷售收入。現用R%表示事先設置的閾值，根據Bauer 和Jannach（2018）[7]的研究，可使商家獲得最大利潤的價格稱為最優價格，若要對售價pn是最優價格的概率進行估計，可運用非參數BootStrap 方法計算pn所對應的Rn值大于或等于閾值R%的BootStrap 置信度Cn。Cn的值即為pn是最優價格的概率估計值，可表示為：

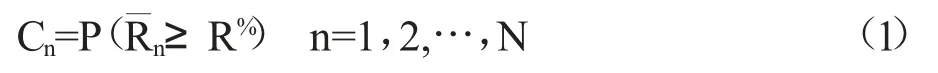
由于BootStrap 置信度Cn描述了真實銷售價格pn是最優價格的概率，故Cn越大，越有理由認為pn是最優價格。

對于閾值R%，最直接的選擇方式是由于商家在銷售的過程中，可能會采取一定的促銷手段銷售商品，從而使某一時間段內的銷量突增，這就會導致該時間段內收入的最大值偏離正常水平，從而影響閾值的大小，過高的閾值可能會導致Cn的估計結果為0，故可適當降低該閾值。參考已有研究對閾值的取值方法，可將閾值R%設置為的90%分位數。

下面對BootStrap 置信度Cn的計算步驟進行說明，具體步驟如下：

①首先設定抽樣次數W，每次抽樣的樣本數據量為Dn，對Rn1，Rn2，…，Rnk進行反復W 次有放回抽樣，得到W 個BootStrap 樣本，將每次抽樣后得到的BootStrap 樣本中的Dn個數據記為R'n1，R'n2，…，R'nk。

②對每一個BootStrap 樣本，計算其Dn個數據的均值，如式（2）所示：

③統計W 個BootStrap 樣本中均值大于或等于閾值R%的樣本數量，記為Xn，則Cn的計算公式如式（3）所示：

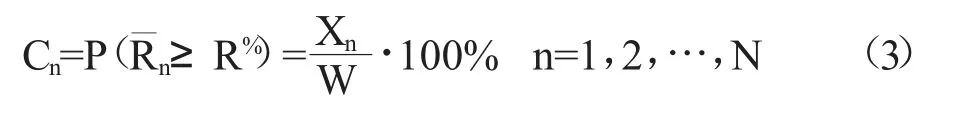
④對{pn｜n=1，2，…，N}中的每一個銷售價格，均按照步驟①、②、③計算其對應的BootStrap 置信度，則可得N 個BootStrap 置信度，即C1，C2，…，CN。

（二）基于核回歸的BootStrap 置信度擬合

Nadaraya 和Watson 于1964年提出了著名的Nadaraya-Watson 核估計。由于Nadaraya-Watson 核估計有且僅有一個參數，相較于其他參數較多的估計方法，該方法不易發生過擬合。

本文使用Nadaraya-Watson 核估計對上一節中的BootStrap 置信度C1，C2，…，CN進行擬合，目的是得到連續價格水平與其對應的BootStrap 置信度之間的非線性函數關系。對給定的核函數K，其Nadaraya-Watson核估計定義如下：

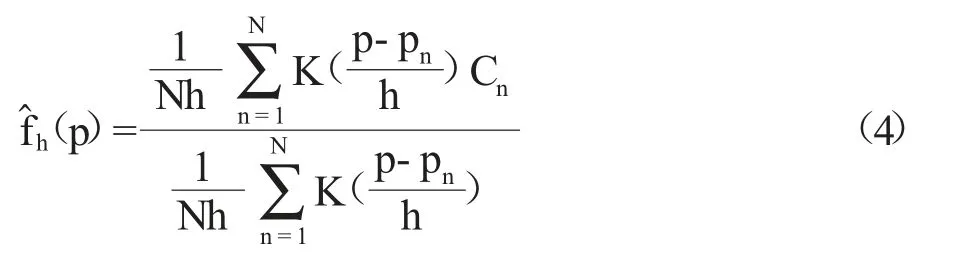
其中，p 表示解釋變量；pn表示真實觀測到的價格點；N 表示價格點的數量；Cn表示價格點pn所對應的BootStrap 置信度的估計；K（·）表示已知核函數，本文選取應用較廣的高斯核函數作為本文的核函數；h 表示根據數據所估計出的窗寬，窗寬h 可以看作是處理偏方差權衡的平滑參數。如果窗寬太小，可能導致數據的過擬合。反之，如果窗寬太大，可能會導致估計過度平均化，偏差和殘差較大，因此窗寬h 的選取尤為重要。本文的最優窗寬選取漸進積分均方誤差方法獲得。

四、實證分析

為驗證上述數據稀疏性處理方法的有效性，本文將分別對模擬生成的稀疏數據和真實的稀疏數據進行稀疏性處理和分析。

（一）稀疏數據生成方法

1.稀疏數據模擬步驟

在對數據進行稀疏性處理前，首先根據易逝品在線銷售數據的特點，模擬生成稀疏數據，具體步驟如下：

①假設商家在線銷售某種易逝商品，其定價區間為[a，b），在[a，b）范圍內采樣N 個不同的數值，記為p1，p2，…，pN，其中p1＜p2＜…＜pN，這N 個數值分別代表該易逝品的N 個銷售價格。

②假設該商品的銷售價格pn保持不變的時長Hn在（0，m）范圍內變動，在（0，m）范圍內隨機采樣N 個不同的整數，記為H1，H2，…，HN，這N 個整數分別代表N 個銷售價格各自保持不變的天數。

③假設每個銷售價格pn（n=1，…，N）對應的日銷售量υn服從參數為λn的泊松分布，即υn～P（λn）。參考Gallego 和Ryzin[13]的研究中關于需求的假設：需求隨著價格的升高逐漸降低，即當p1＜p2＜…＜pN時，有λ1＞λ2＞…＞λN。假設每個銷售價格pn對應的日銷售量均值λn在范圍（c，d）內變動，先在范圍（c，d）內采樣N 個不同的數值，記為λ1，λ2，…，λN，其中λ1＞λ2＞…＞λN，然后根據N 個泊松分布υ1～P （λ1），υ2～P （λ2），…，υN～P（λN），分別模擬生成N 組數據，每組數據表示每個銷售價格在其價格保持不變的時長內的若干個日銷售量值。在模擬過程中，要保證這N 組數據中各組數據的數據量與H1，H2，…，HN的值對應相等。

④將步驟③中模擬生成的N 組銷售量分別與N個銷售價格對應相乘，得到N 組銷售收入數據，每組收入數據表示每個銷售價格在其保持不變的時長內的若干個日銷售收入值。

2.參數設置

為更好模擬出具有易逝品在線銷售數據特點的稀疏數據集，本文將基于前文選取的真實數據集中各變量的數值，對上述模擬步驟中的各參數進行合理設置。由前文可知，在真實數據集中，銷售價格在11.80—49.90 元之間變動，銷售價格的總數量為50 個，銷售價格保持不變的時長Hn在9—204 天之間變動，日銷售量的均值大約為197 件。現參考真實數據集中的數值，對即將生成的模擬數據集中的參數進行設置，其設置原則為：與真實數據集有一定差異，但不能完全脫離實際。由于數據模擬過程中可能會受到隨機因素的干擾導致達不到較為理想的效果，為增加數據稀疏性處理結果的可信度，本文將通過不同的參數設置及價格采樣方式生成兩個有一定差異的模擬數據集，使第一個模擬數據集（模擬數據集1）具有第二類稀疏數據的特點，即銷售價格如何影響平均銷售收入的有效數據點較少，而第二個模擬數據集（模擬數據集2）具有第三類稀疏數據的特點，即價格數據點是稀疏分布的。

假設商家在線銷售的某種易逝品的定價區間為[50，100），商家將各售價保持不變的時長Hn控制在（0，100）范圍內，故設置a=50，b=100，m=100。對模擬數據集1，借鑒王芷陽[14]在研究中使用的數據采樣方式，在[50，100）上均勻采樣30 個不同的數值pi（i=1，2，…，30），并假設模擬數據集1 中日銷售量均值λn在（100，200）內變動，故參數設置為：N=30，c=100，d=200。對模擬數據集2，借鑒周啟堃[15]在模擬稀疏分布的數據時的采樣方法，在[50，100）上抽取50 個不同的數值pi（i=1，2，…，50），其中區間（50，60）、（60，70）、（80，90）和（90，100）各有5 個樣本數據，而區間（70，80）內有30 個樣本數據，并假設模擬數據集2 中日銷售量均值λn在（150，250）范圍內變動，故參數設置為：N=50，c=150，d=250。

3.稀疏數據生成效果展示及分析

為檢驗使用上述方法生成的兩個模擬數據集是否具有各自不同的稀疏性特點，下面對模擬數據集1和模擬數據集2 的生成效果進行展示與分析。

圖3是模擬數據集1 中各銷售價格保持不變的時長Hn的分布直方圖，Hn的均值為51.9 天。從圖3可以看出，各價格保持不變的時長Hn的取值分布在0—100 天內，大部分價格保持不變的時長均超過一個月。由此可見，模擬數據較好地模擬出了易逝品售價長時間保持不變的特點。

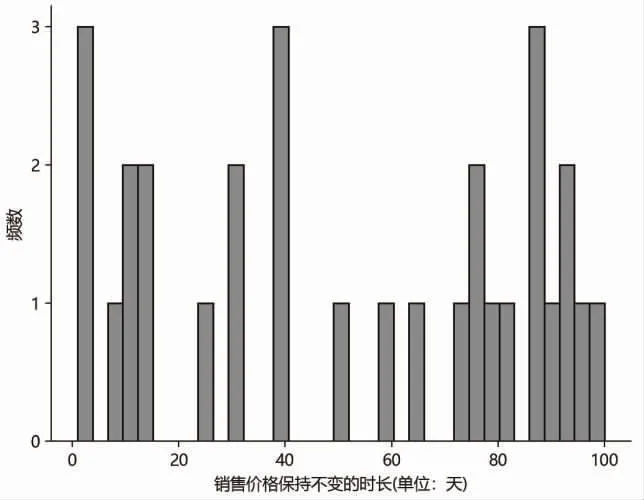
圖3 銷售價格保持不變的時長的分布直方圖（模擬數據集1 ）

圖4是根據模擬數據集1 中各銷售價格及其對應的平均銷售收入繪制的散點圖，這里的平均銷售收入指某銷售價格在其保持不變的時長內的日銷售收入平均值。圖中水平虛線代表所有銷售價格對應的平均銷售收入的均值。從圖4可以明顯看出，絕大部分的點較為均勻地分布在虛線上下400 元范圍內，平均銷售收入的波動范圍較小，且數據點整體沒有明顯上升或下降的趨勢，只有個別數據點對應的平均銷售收入波動較大，無法得出銷售價格與平均銷售收入之間的關系，表現銷售價格如何影響銷售收入的有效數據點很少。由此可見，模擬數據集1 較好地模擬出了第二類稀疏數據的特點。

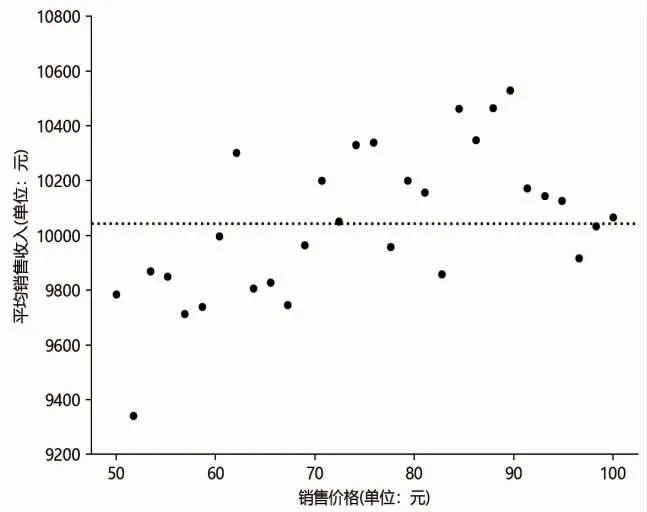
圖4 銷售價格-平均銷售收入散點圖（模擬數據集1 ）

圖5是根據數據集2 中各銷售價格及其對應的平均銷售收入繪制的散點圖，這里的平均銷售收入指某銷售價格在其保持不變的時長內的日銷售收入平均值。圖中水平虛線代表所有銷售價格對應的平均銷售收入的均值。從圖5可以明顯看出，銷售價格區間（50，60）、（60，70）、（80，90）和（90，100）內各有5 個數據點，而（70，80）內有30 個數據點，數據點分布嚴重不均。銷售價格區間（70，80）內的數據點明顯較密集，而其他區間內的數據點非常稀疏，數據點分布差距大，價格數據是稀疏分布的。由此可見，模擬數據集2較好地模擬出了第三類稀疏數據的特點。

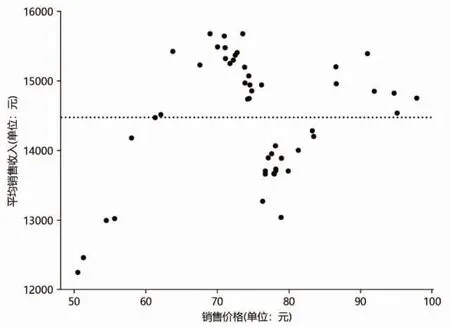
圖5 銷售價格-平均銷售收入散點圖（模擬數據集2 ）

（二）數據稀疏性處理及分析

本文將運用前文所述的數據稀疏性處理方法對模擬數據集1、模擬數據集2 以及真實銷售數據集進行處理和分析，其中BootStrap 抽樣次數W 設置為W=1000。

1.模擬數據集的稀疏性處理結果

圖6是對模擬數據集1 進行稀疏性處理后的結果，其中，核回歸的窗寬是根據漸進積分均方誤差方法計算得到的最優窗寬，即h=8.57。從圖6可以看出，經過稀疏性處理后，銷售價格與其對應的BootStrap 置信度之間呈現出非線性關系，隨著銷售價格水平的升高，其對應的BootStrap 置信度先增大后減小。

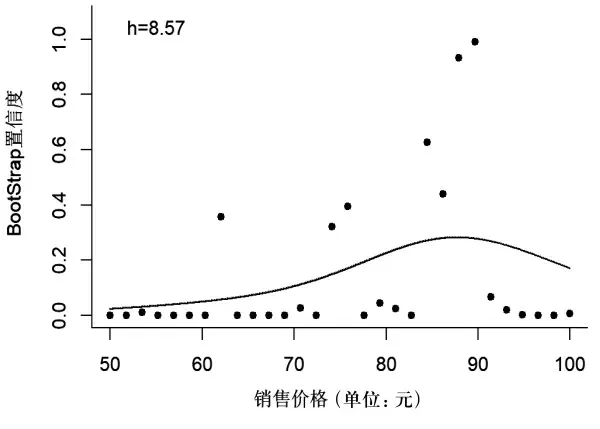
圖6 銷售價格-BootStrap 置信度擬合圖（模擬數據集1 ）

圖7是對模擬數據集2 進行稀疏性處理的結果，其窗寬是根據漸進積分均方誤差方法計算得到的最優窗寬，即h=2.52。從圖7可以看出，經過稀疏性處理后，銷售價格與其對應的BootStrap 置信度之間呈現出非線性關系。當銷售價格大約處于58—68 元之間和80—90 元之間時，隨著銷售價格水平的升高，其對應的BootStrap 置信度逐漸增大；當銷售價格大約處于68—80 元之間、90—100 元之間時，隨著銷售價格水平的升高，其對應的BootStrap 置信度逐漸減小。

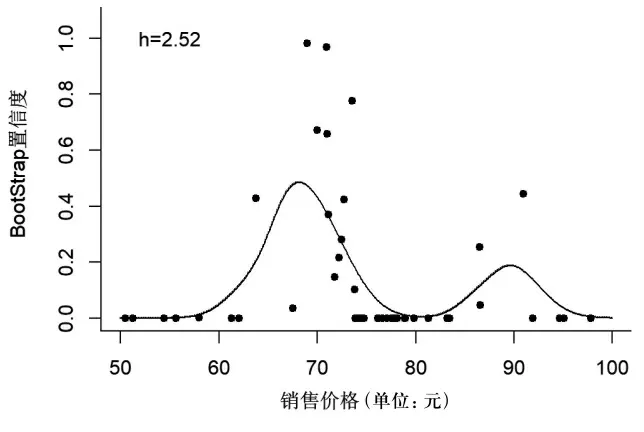
圖7 銷售價格-BootStrap 置信度擬合圖（模擬數據集2 ）

2.真實銷售數據集的稀疏性處理結果

圖8是對前文描述的真實銷售數據集進行稀疏性處理后得到的結果，其核回歸函數的窗寬是根據漸進積分均方誤差方法獲得的最優窗寬，即h=5.15。從圖8可以看出，隨著價格水平的升高，其對應的BootStrap置信度先逐漸增大后逐漸減小，通過核回歸曲線可以清晰地看到價格水平與其對應的BootStrap 置信度之間的非線性關系。

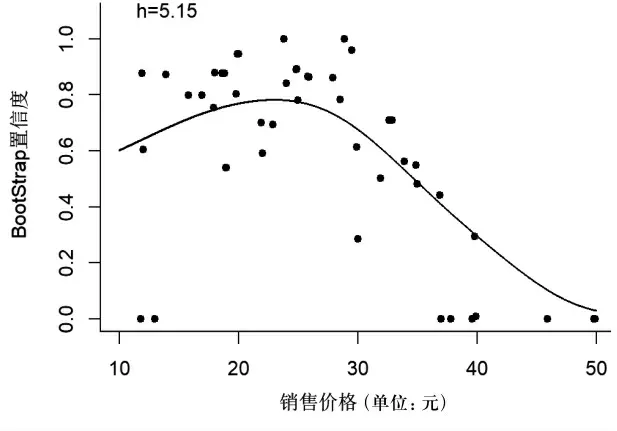
圖8 銷售價格-BootStrap 置信度擬合圖（真實數據集）

隨著價格水平的升高，其對應的BootStrap 置信度先增大后減小的原因可能為：大部分消費者所能接受的最高售價大約為23 元，當商品的售價超出23 元時，消費者通常不會購買商品，導致商品在售價達到23 元以后，銷售量急劇下降，銷售收入隨之下降。BootStrap置信度是基于對銷售收入觀測值反復抽樣作出的估計，故BootStrap 置信度隨價格水平變化的規律與銷售收入隨價格水平變化的規律具有一定的相似性。

五、結論

實際銷售過程中，商家的銷售收入是實時產生和變化的，因此具有較大的不確定性。本文對易逝品銷售數據的稀疏性處理中，運用BootStrap 方法估計每個價格點對應的BootStrap 置信度，相當于利用概率思維量化了這種不確定性，之后又運用Nadaraya-Watson核回歸擬合各離散價格點對應的BootStrap 置信度，Nadaraya-Watson 核回歸不僅能夠平滑相鄰點之間較大的波動。增加結果的可靠性，還將真實數據集中沒有但又處于定價區間內的價格點的BootStrap 置信度都作出了估計，不遺漏定價區間內的任何一個價格。通過核回歸擬合結果不僅可以清晰地看到價格水平與其對應的BootStrap 置信度之間的非線性函數關系，還可以看出整個定價區間中價格的優劣，從而為商家制定定價策略提供一定的決策依據，也為后續的定價研究奠定了基礎。◆