基于Rashba和Dresselhaus自旋軌道耦合的非均勻量子線中電子傳輸特性研究

陳 妍 劉 誌 黃 朵

（1.江西理工大學 電氣工程與自動化學院，贛州 341000；2.江西理工大學 信息工程學院，贛州 341000）

目前，半導體中的自旋輸運特性因其在未來自旋電子器件中具有巨大潛力而獲得了人們越來越多的關注[1-2]。這個領域最重要的問題是如何提供可行的方法來產生、操作、存儲和檢測半導體材料中的自旋極化電子。由塊體材料的反轉不對稱性引起的Dresselhaus自旋軌道耦合（Spin Orbit Coupling，SOC）和由結構反轉不對稱性引起的Rashba自旋軌道耦合，被認為是實現這些目標的手段。本文采用非平衡格林函數方法，結合Landauer-Büttiker近似，研究基于Rashba和Dresselhaus兩種自旋軌道耦合的非均勻量子線中的自旋輸運性質。

1 模型與分析

研究的凹型非均勻量子線的結構如圖1所示。Rashba和Dresselhaus自旋軌道耦合夾在兩條正常的金屬導線之間，如圖1（a）所示。相應的實驗裝置方案如圖1（b）所示。使用(x,y)平面上的二維電子氣（Two-Dimensional Electron Gas，2DEG）來定義非均勻量子線。頂柵產生橫向限制勢V(x,y)用于描繪非均勻量子線后柵用于調諧Rashba自旋軌道耦合強度。非均勻量子線（Quantum Wire，QW）窄中心部分的寬度為D，長度為H，左右寬部分具有相同的長度L和相同的寬度W。量子線的左右兩邊都連接著寬度為W的半無限長理想導線。

為了研究系統的電子傳輸特性，將其離散成一個正方形晶格。在Rashba和Dresselhaus自旋軌道耦合上具有緊密約束的哈密頓量在正方形晶格上的定義為

圖1 “凹型”非均勻量子線的結構及實驗裝置圖

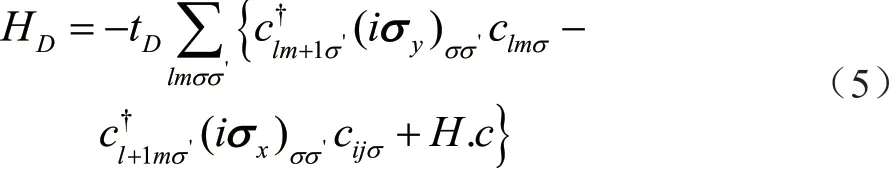
式中：HO為不含自旋軌道耦合時的哈密頓量；V為外加限制勢能；HR為含Rashba自旋軌道耦合時的哈密頓量；HD為含Dresselhaus自旋軌道耦合時的哈密頓量為lm格點自旋σ（σ=↑,↓）的產生（湮滅）算符；σx和σy為泡利矩陣；εlmσ=4t為格點能，其中為格點之間的勢能，這里 ? =h/2π，h為普朗克常數；m*（m*=0.067me）和a分別為電子的有效質量和晶格常數；Vlm為格點上額外限制勢；HR為Rashba自旋軌道耦合項；tR=α/2a為Rashba SOC強度，其中α為Rashba常數；HD為Dresselhaus SOC自旋軌道耦合項，tD=β/2a為Dresselhaus SOC強度，其中β為Dresselhaus常數；σ′為自旋方向，σ′=↑或↓；H.c.是公式中前兩項的共軛項。

基于哈密頓量，用非平衡格林函數（Non-Equilibrium Green Functions，NEGF）可以得到散射電子態的出射波函數[3]。隨后采用Landauer-Büttiker公式得到兩端的自旋相關電導[4-5]，即

式中：e為電子電荷量；h為普朗克常數；左右兩端導線引起的自能分別用和表示；Tr為對凹型非均勻量子線整個空間自由度求跡。另外，凹型非均勻量子線整個系統含有自能的推遲格林函數為Gr，而超前格林函數為Ga。

電子從左邊入射端電極透射到右邊出射端電極的概率在Z方向上的總電導定義為

由自旋極化電子輸運引起的右邊出射端局域自旋密度的變化在Z方向上的自旋極化率定義為

選擇的物理量為具有典型電子密度即每平方厘米約為2.5×1011V·s的高遷移率GaAs/AlxGa1-xAs異質結結構[6]。所有能量都由跳躍能量t（t=1）歸一化，量子線的其他參數固定為W=20a、D=7a、L=10a和H=30a，緊密結合模型的晶格間距設為a=1 nm。

2 結果和討論

圖2（a）為凹型非均勻量子線左側部分的能量子帶色散；圖2（b）為凹型非均勻量子線右側部分的能量子帶色散，a-1為晶格常數的倒數（相當于單位），k為波數。Rashba SOC的強度設置為tR=0.158，Dresselhaus SOC的強度設置為tD=0.158。

E≥0.154 1 meV，左 側 部 分 具 有 一 個 子 帶。E≥0.206 1 meV，右側部分有兩個子帶。圖3（a）為自旋向上（實曲線）和自旋向下（虛曲線）電子的電荷電導與能量的關系。圖3（b）為與圖3（a）相應的自旋極化率隨電子入射能量的變化。可以看到，電荷電導呈階梯狀結構，且電導顯示自旋向上電子和自旋向下電子之間的臨界差異。當入射能量E=0.154 1 meV時，左（右）部分最低的一（兩）對子帶成為傳播模。隨后，Rashba和Dresselhaus自旋軌道耦合引起的子帶混合導致非零的自旋極化電流。在對應右側子帶極小值的電子能量即E=0.154 1 meV處，獲得了大的自旋極化|PZ|=0.63。

量子線中間較窄部分的能量子帶發生色散。Rashba和Dresselhaus自旋軌道耦合的強度分別取為tR=0.158和tD=0.158。

圖2 “凹型”非均勻量子線能量子帶色散

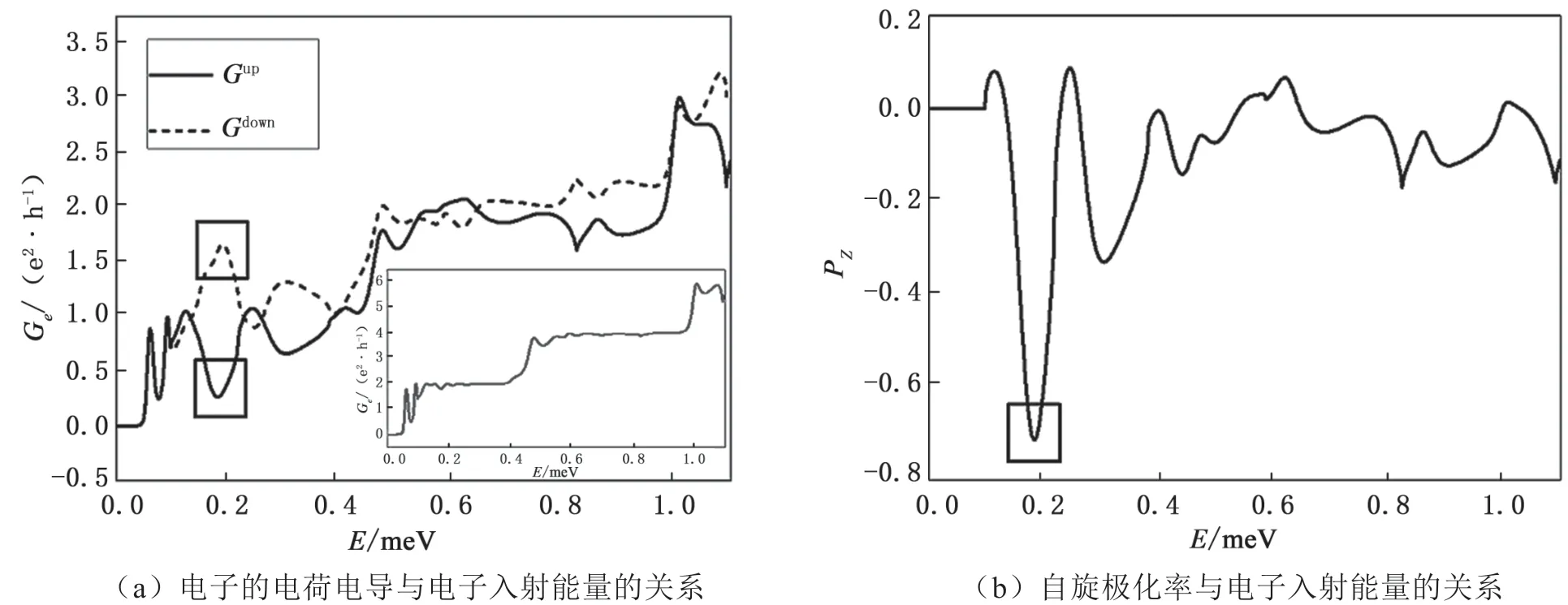
圖3 電子入射能量的影響因素

如圖4所示，Dresselhaus SOC強度tD=0.0（實曲線）、tD=0.108（虛曲線）和tD=0.158（點曲線）時，電子自旋極化率隨入射能量變化，其中Rashba SOC強度設置為tR=0.158。

研究非均勻量子線相對于Rashba和Dresselhaus SOC的電子自旋極化。首先，研究Dresselhaus SOC對電子自旋極化的影響。如圖4所示，對于tD=0.0時（即沒有Dresselhaus SOC的情況），在入射能量E=0.206 1 meV時，觀察到|PZ|=0.78的自旋極化值的峰值。當tD≠0.0（即包括兩個SOC）時，仍然存在較大的電子自旋極化率。例如，即使當Dresselhaus SOC強度tD=0.158時，也表現出|PZ|的高自旋極化率，且在入射能量E=0.154 1 meV時可得到自旋極化率|PZ|=0.63。隨著Dresselhaus SOC強度的增加，自旋極化曲線中的峰向左稍移，高度降低。這源于有效電位與Dresselhaus SOC之間的相互作用，也表明可以通過改變Dresselhaus SOC強度來調制自旋極化。

圖4 電子自旋極化率隨入射能量變化

對于自旋非極化電子注入，計算可得到自旋極化與Rashba和Dresselhaus SOC強度的函數關系，入射能量E=0.154 1 meV。

電子自旋極化值對SOC強度的設定值很敏感。為了進一步研究Rashba和Dresselhaus SOC的組合影響，研究不同強度的Dresselhaus和Rashba SOC在非均勻量子線中的電子自旋極化隨入射能量E=0.154 1 meV的變化。如圖5所示，當Dresselhaus SOC和Rashba SOC同時加入到非均勻量子線上時，電子自旋極化的等高線圖表現為“圓形”分布，且具有基本相同的作用。

圖5 電子自旋極化率的等高線圖

3 結語

由于非均勻量子線的鏡面對稱性被破壞，即使同時存在Rashba和Dresselhaus SOC，仍然可以誘導出較大的電子自旋極化。此外，實驗結果表明，系統的自旋極化隨Dresselhaus和Rashba SOC的變化呈“圓形”分布，表明這兩個SOC在誘導自旋極化方面起著基本相同的作用。因此，人們可以通過調制Rashba或Dresselhaus SOC強度來調節系統的自旋極化，從而使提出的結構可能在不使用任何磁性材料或施加磁場的情況下制造多功能半導體自旋電子器件。