基于Encoder-Decoder LSTM的電梯制動滑移量預測方法研究

蘇萬斌，江葉峰，徐彪，易燦燦

(1.嘉興市特種設備檢驗檢測院，浙江 嘉興 314000；2.武漢科技大學，湖北 武漢 430081)

0 引言

電梯作為現今與國計民生息息相關的重要特種設備，已被我國廣泛使用。截至2020年底，全國電梯的保有量為786.55萬臺。曳引式電梯作為最常見垂直運輸設備，長時間使用后，電梯的曳引輪和鋼絲繩之間會因為磨損等原因，使得電梯的曳引能力降低，而電梯曳引能力的下降是電梯事故的最主要原因之一[1]。現今城市老舊電梯數量越來越多，曳引能力下降而造成電梯事故也愈發常見，因此實現對老舊電梯的曳引能力可靠性進行預測已是現今亟待解決的問題。

現有關于電梯曳引能力判斷的研究主要有兩種，一種為通過專門的裝置對鋼絲繩兩端施加拉力，記錄滯留工況下引起鋼絲繩滑移所需的拉力；另一種是通過記錄在空載上行制動時的鋼絲繩滑移量，判斷鋼絲繩曳引輪系統的可靠性[2-3]。在實際應用中，對鋼絲繩施加牽引力以驗證曳引能力成本較高，而通過測量電梯鋼絲繩緊急制動的滑移量來反映鋼絲繩曳引性能，具有操作簡單、結果可靠、可量化的優點，能很好地反映由于電梯老舊退化而導致的曳引能力降低趨勢及由于維護而導致的曳引能力的回升趨勢[4-5]。因此，通過對鋼絲繩滑移量的預測，可以有效反映一段時間內的電梯曳引系統曳引能力變化趨勢[6]。

電梯由于作為運輸工具的特殊性，其滑移量具有非線性特征，且由于電梯有維修周期，電梯曳引能力會有周期性的回升。此外，由于電梯的特殊性，對電梯滑移數據的測量無法頻繁進行，因此無法獲得大量的數據樣本量，這些都使得對電梯制動滑移量的預測變得非常困難。因此，本文采集并分析電梯每季度及年維護后的空載上行實驗滑移量，利用基于時間序列特征的深度學習算法，實現對未來一年時間內的滑移量進行預測，并使用現有觀測數據對理論方法進行可行性驗證。

常用于時間序列分析的深度學習方法有BP神經網絡、循環神經網路RNN、長短期記憶網絡LSTM等。BP神經網絡發展時間長，具有模型清晰、結構簡單的特點，但卻難以處理非線性問題[7]。循環神經網絡[8](recurrent neural network, RNN)對序列的非線性特征進行學習具有一定優勢，但在進行較長預測時，存在梯度消失和效果降低等問題，同時由于預測長期數據時，后期數據會因為前期預測的誤差而造成預測精度降低。LSTM(long short-term memory)神經網絡可以看作是一類改進后RNN，其優勢是能夠更好地學習序列長期的規律[9-10]，在交通流預測及股市預測等時序預測領域有較好的應用效果。LSTM神經網絡結構繼承了RNN的鏈式循環結構，并且彌補了RNN在學習過程中對于長期數據效果下降的問題，在長間隔、非線性時間序列的預測方面有較好的效果[11]。但作為RNN的改進版本，其同樣無法解決多步預測時的誤差累積問題。

針對單步預測導致的誤差累積放大的問題，本文采用編碼器-解碼器(Encoder-Decoder)框架進行處理。Encoder-Decoder結構[12]在自然語言處理等領域有著出色的表現，編碼器將序列信號壓縮成一個受參數約束的固定維度語義向量，再通過解碼器對該語義向量進行解析，并使用遞歸方式將預測結果反饋至網絡中，實現單變量的多步預測，避免了單步預測所造成誤差累積。基于此，本文采用Encoder-Decoder LSTM模型對電梯滑移量進行預測，并利用電梯滑移量實際觀測數據對分析結果進行評價。

1 基于Encoder-Decoder LSTM模型的預測技術

1.1 LSTM模型

LSTM作為RNN的改進算法，其重要改進是通過增加遺忘門、輸入門、輸出門獲得變化的自循環權重，以此避免RNN所面臨的梯度消失問題。這使得LSTM可以在RNN效果的基礎上記憶更長的時序信息，增加預測精度。LSTM的單元結構如圖1所示，每個LSTM單元中存在細胞(cell)用于描述單元當前狀態，同時在單元中存在著3類控制門，即用于控制輸入的輸入門(input gate)，控制數據輸出的輸出門(output gate)及控制單元狀態的遺忘門(forget gate)[13]。當控制門打開時，表示允許所有信息通過；當控制門關閉時，表示不允許任何信息通過。

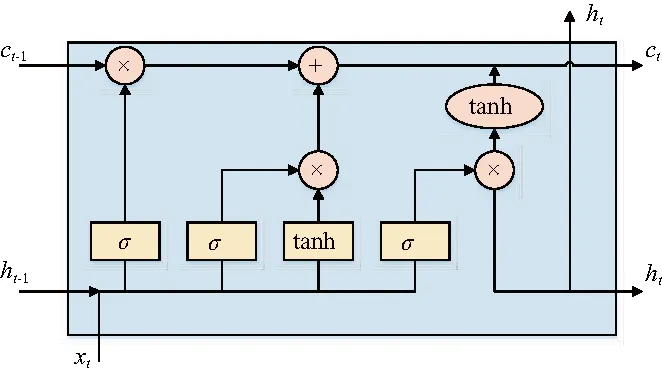
圖1 LSTM結構

遺忘門、輸入門、輸出門方程如下：

ft=σ(Wf·[ht-1,xt]+bf)

(1)

it=σ(Wi·[ht-1,xt]+bi)

(2)

ot=σ(Wo·[ht-1,xt]+bo)

(3)

(4)

(5)

式中：tanh為激活函數；Wc、bc分別是單元狀態的權矩陣和偏置。當前網絡的輸出值ht由下式計算：

ht=ot·tanh(ct)

(6)

1.2 Encoder-Decoder模型

Encoder-Decoder模型，又叫做編碼-解碼模型,常被應用于seq2seq問題[14]，即根據一個輸入序列X來生成另一輸出序列Y。本文中運用其解決電梯滑移量的多步預測。編碼過程是將輸入序列轉化成一個固定長度的向量；解碼時再將所生成的語義向量轉化成設定的輸出序列。

本文使用LSTM作為編碼層和解碼層，組成Encoder-Decoder LSTM模型(圖2)。

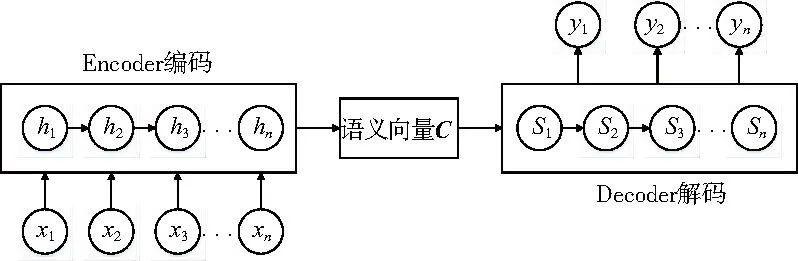
圖2 Encoder-Decoder模型結構

圖2中的h代表編碼端的隱含層狀態，S則代表解碼端的隱含層狀態。在編碼階段，h為當前時刻的隱含層狀態，由當前時間的輸入x及上一時間的隱含層狀態ht-1計算得，公式為

ht=f(ht-1,xt)

(7)

之后可將各時刻的隱含層狀態匯總得到一個固定長度的中間語言向量C：

C=L(h1,h2,h3,…,hn)

(8)

L一般可以選用任一RNN，本文選用LSTM。解碼階段可以視為編碼階段的逆過程，解碼器根據編碼階段生成的語義向量C及歷史的的滑移數據序列y來預測之后的滑移數據。

(9)

Encoder-Decoder作為一種深度學習框架，一般會搭配RNN一起使用，用于解決輸入與輸出不同時的問題，本文使用其來解決傳統LSTM算法在多步時間序列，會由于前面預測值作為歷史數據使用導致之后數據的誤差越來越大，Encoder-Decoder將時間序列表達為向量，并使用解碼器對向量解讀并預測，規避了該問題[15]。

1.3 基于Encoder-Decoder LSTM模型的電梯滑移量預測方法

預測流程如圖3所示。輸入為已知的訓練集數據，通過歸一化以后，經過作為編碼器的LSTM網絡層，編碼器將歷史數據進行編碼并生成固定長度語義向量。語義向量大小由隱含層大小決定，之后 將語義向量輸入同為LSTM網絡層的解碼器進行解碼，返回多步的預測結果，實現單一變量數據的多步預測，其具體步驟如下。

圖3 電梯滑移量預測模型結構

數據采集：按每季度頻率定期進行空載上行制動實驗，采集電梯的制動滑移數據，在以年為單位進行維修后，收集維修前、維修后兩段數據。

歸一化：依照目標電梯的標準參數及國標要求，計算出空載上行制動實驗允許最大滑移量，使用min-max標準化方法對滑移量歷史數據進行歸一化處理，使數據映射到[0，1]的區間。

Encoder編碼層：通過一個單層LSTM將輸入單變量時間序列編碼成一個語義向量，作為解碼層的輸入，語言向量長度由隱含層大小決定。

Decoder解碼層：通過一個單層LSTM對編碼層輸出的語義向量進行解碼。

全連接層：通過全連接層將解碼層輸出轉化成所需的多步預測結果。

2 實驗數據分析

通過專業曳引系統檢測裝置，將輪狀采集器安裝在試驗機的鋼絲繩與曳引輪上進行位移采集。采集電梯轎廂質量為1 300 kg，額定載重2 000 kg，曳引輪直徑640 mm，平衡系數0.48，傳動系統減速比32，曳引比2，試驗速度為額定速度1 m/s，工況為空載上行緊急制動。本文使用采集的50組數據用于實驗分析，并分別使用LSTM、RNN及Encoder-Decoder LSTM模型對數據進行預測，并對比3種模型的預測結果，驗證所提方法的可靠性。

2.1 實驗數據

實驗所用電梯制動滑移數據，通過對某區域不同使用時長的多臺同型號貨梯進行空載上行制動實驗，采集制動時電梯曳引輪位移、鋼絲繩位移等數據，獲得相同工況下每年5組，跨度10年的共50組電梯制動滑移數據，每年5組數據中，前4組為各季度測得滑移量，最后1組為常規維護后的滑移數據，滑移數據如圖4所示。本文將50組數據分為2部分，使用前44組數據對模型進行訓練，使用最后6組數據進行模型有效性的驗證。

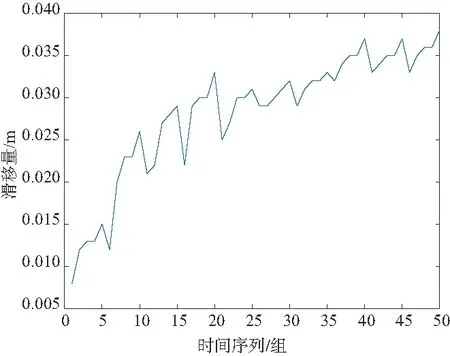
圖4 電梯空載上行緊急制動滑移數據

2.2 數據預處理

本文使用Min-Max函數對采集的滑移量數據做歸一化處理，通過將滑移量數據規約至[0,1]區間，提高各預測模型的收斂速度和預測能力。歸一化公式為

(10)

式中：xi為原始數據；x′i為歸一化后數據；xmax為采集數據中的最大值；xmin為采集數據中的最小值。

2.3 參數設置及指標選取

文中設置400個隱含單元并使用relu函數作為激活函數，MSE作為損失函數，Adam作為求解器。為防止訓練中出現梯度爆炸，影響預測結果，將梯度閾值設置為1。模型設置初始學習率0.005，150輪訓練后通過乘以因子0.2來降低學習率至0.000 1。

為了能對各模型的預測結果準確性進行客觀評價，分別對各模型預測結果計算其方均根誤差(RMSE)與平均絕對誤差(MAE)。通過比對進行評判，RMSE與MAE值越小，預測效果越好。

2.4 電梯緊急制動滑移量預測

圖5為基于RNN模型的電梯滑移量預測結果。從圖中可以看出，RNN模型計算得到的預測結果與實際數據趨勢基本一致，但整體誤差較大，預測值相較于真實值仍有不小差距。這是由于RNN模型在接受的輸入時間序列過長時，模型將喪失學習到先前輸入序列的信息，因而導致預測效果較差。模型預測結果的方均根誤差及平均絕對誤差經過計算為：REMS=0.001 8；MAE=0.001 6。

圖5 RNN預測結果

圖6為基于LSTM的滑移量預測。可以看出整體預測效果好于RNN預測，但由于單步預測導致的誤差累積，整體效果仍然不理想。雖然經過誤差統計得出LSTM模型整體預測效果優于RNN模型，但由于滑移量是波動較大的數據，預測結果仍與實際值存在一定差距。這是由于LSTM模型本身在面對更長的輸入序列時所存在的局限性造成的。模型預測結果的方均根誤差及平均絕對誤差經過計算為：REMS=0.000 952 72；MAE=0.001 1。

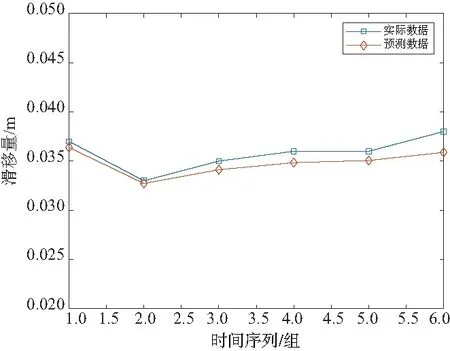
圖6 LSTM預測結果

圖7為基于Encoder-Decoder LSTM模型的電梯滑移量預測結果。通過前44組數據訓練模型后，對后6組數據進行預測，發現Encoder-Decoder LSTM模型預測的結果都明顯優于上述兩種方法，模型成功地從歷史數據中學習出年滑移量變化趨勢。經過理論計算，模型預測結果的方均根誤差及平均絕對誤差為：REMS=0.000 711 24；MAE=0.000 776 41。

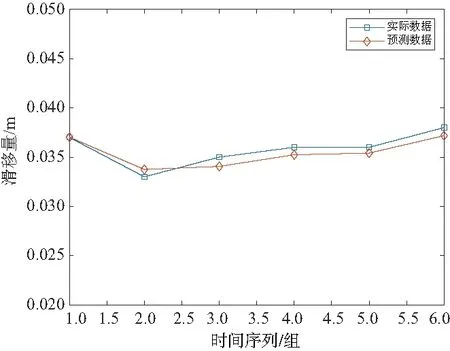
圖7 Encoder-Decoder LSTM模型預測結果

最后，通過表1列出了不同時間序列預測方法對滑移量數據分析的效果。由表1可以看出，Encoder-Decoder LSTM模型在對電梯制動滑移量的預測上效果明顯優于RNN及LSTM模型。Encoder-Decoder LSTM相較于LSTM的預測效果分別提高了25.4%和29.6%。由此可以說明，在單變量多步預測問題上，Encoder-Decoder LSTM模型有著更優于其他模型的效果，該模型能較好地解決電梯緊急制動滑移量的預測問題。

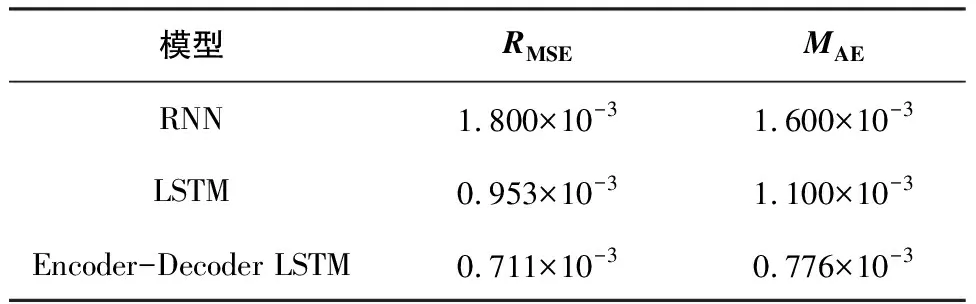
表1 對比預測結果評價指標

3 結語

針對電梯曳引能力定量預測問題，本文在LSTM時間序列預測模型的基礎上，結合Encoder-Decoder框架，解決了傳統LSTM難以進行長期預測的問題，實現高精度的單變量多步預測。本文通過Encoder-Decoder LSTM模型對電梯制動滑移數據進行預測，預測結果的方均根誤差REMS=0.000 711 24,平均絕對誤差MAE=0.000 776 41，這表明模型在單變量多步的電梯制動滑移數據的預測上可以達到較好效果，對于電梯曳引性能的可靠性預測具有一定的參考意義。