一種鏡像電流源荷控憶阻器及其Lorenz 混沌電路研究

代云中，莊圣賢，李美容

（1.宜賓職業技術學院 智能制造學院，四川宜賓，644003；2.西南交通大學 電氣工程學院，四川成都，611756）

0 引言

20世紀80年代Chua[1～3]通過物理的對稱性給出一種憶阻器，由于憶阻器具有非線性與記憶等特性，使得憶阻器在混沌系統[6～10]、阻變存儲器[5～6]、現場可編程邏輯門陣列[14,11]、人工神經網絡[12]、保密通信[11]、電力電子[13,14]、圖像處理[11,12]和音頻信號[16]等方面有廣泛使用。近年來，國內外學者研究了多種具有不同結構的含有憶阻器的混沌電路[3～6,15-17]。LOChua等給出一種分段磁控憶阻器（Magnet-Controlled Memristor,MCM）替換chua系統中的二極管，得出了含有非線性MCM的chua混沌系統[3,6]。文獻[7]采用分段MCM并聯在Lorenz電容兩端[7]，給出一種含MCM的Lorenz混沌系統，然而分段函數是階躍變化的，難以在實際工程中實現。但是文獻[7]的研究表明，與傳統Loren相比，含MCM的Lorenz系統表現出了完全不同的非線性行為[7,16]。

由于現有工業產品中還無法造出憶阻器，為了研究含憶阻器的Lorenz系統的動力學行為。上述研究憶阻器使用比例積分（Proportional Integral，PI）電路、乘法器等搭建憶阻器的電路[5～9]。但是因為PI電路中積分漂移的作用，使憶阻器的輸出信號與真實的憶阻器有較大不同，進而難以對含有憶阻器的混沌系統的真實動力學行為進行研究[8～9,15～17]。

本文首先提出采用鏡像電流源的荷控憶阻器；接著將給出含荷控憶阻器的Lorenz混沌系統（Lorenz with Charge-Controlled Memristor, Lorenz -CCM）；最 后，對 Lorenz-CCM系統進行數值仿真和實驗驗證。

1 荷控憶阻器

惠普（HP）憶阻器是一種荷控憶阻器，由文獻[1]可知其憶阻值為：

式（1）中：

μv電子遷移率，則憶阻器的輸入電流i(t)和輸入電壓u(t)關系為[1]：

式(2)中φ(t)為磁通，q(t)為電荷。

當取aq=1，bq=450，u(t)=sin(2πft)，f=50Hz時，可得：

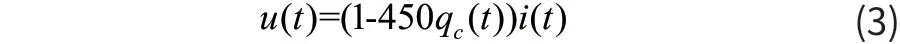
將u(t)代入（3）式，進行數值仿真可得憶阻器的u-i曲線，如圖1所示。從圖1中可知，呈現出一個斜“8”字形的緊磁滯回線，與Chua的荷控憶阻器具有一樣的u-i特性[6]。

圖1 u-i曲線

由(3)式的憶阻器數學模型，本文設計了一種基于鏡像電流源的荷控憶阻器，如圖2所示。

i(t)通過由N型(MN0～MN4)與P型金氧半場效晶體管(Metal-Oxide-Semiconductor Field-Effect Transistor, MOSFET) (MP0～MP4)構建的鏡相電路后，分別流入到電容CT與電阻RT中，獲得CT的電壓VC=qc(t)/CT和RT的電壓i(t)×RT，qc(t)為CT的電荷。圖2中VDD和VSS分別為+5V和-5V。VC與i(t)×RT再經過乘法器(AD633)后可得Vx為：

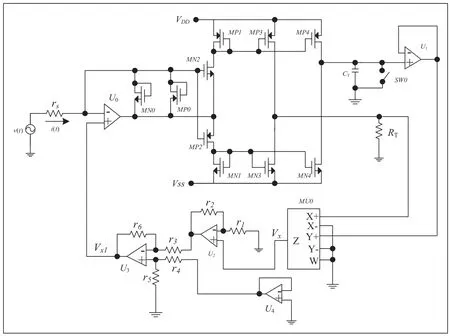
圖2 荷控憶阻器

Vx通 過（U2，U3，U4，r1，r2，r3，r4，r5，r6）組 成 的反相比例電路可得Vx1：

接著，通過圖2可知：

所以，在i(t)輸入下可知鏡像電流源荷控憶阻器v(t)和i(t)的關系為：

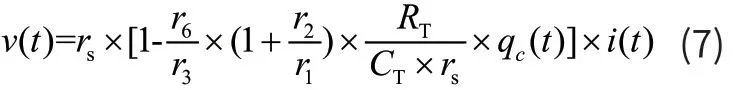
然后，當aq=1，bq=450時，對照(3)式和(7)式，可計算出鏡像電流源荷控憶阻器的電路參數如表1所示。

表1 鏡像電流源荷控憶阻器仿真參數

根據圖2的電路結構和表1的計算出的鏡像電流源荷控憶阻器電路參數，采用Pspice搭建電路對圖2中設計的荷控憶阻器進行電路仿真。當u(t)=sin(2πft)，f=50Hz時的電路仿真結果如圖3所示。圖3(a)、(b)、(c)分別為u(t)，i(t)和u-i特性曲線。從圖3中可知i(t)的相位滯后于u(t)。u-i曲線是一個斜“8”字形的類緊磁滯回線的特性，且關于中心原點對稱，不存在積分漂移特征。所以，仿真結果驗證了鏡像電流源荷控憶阻器電路設計的正確性。

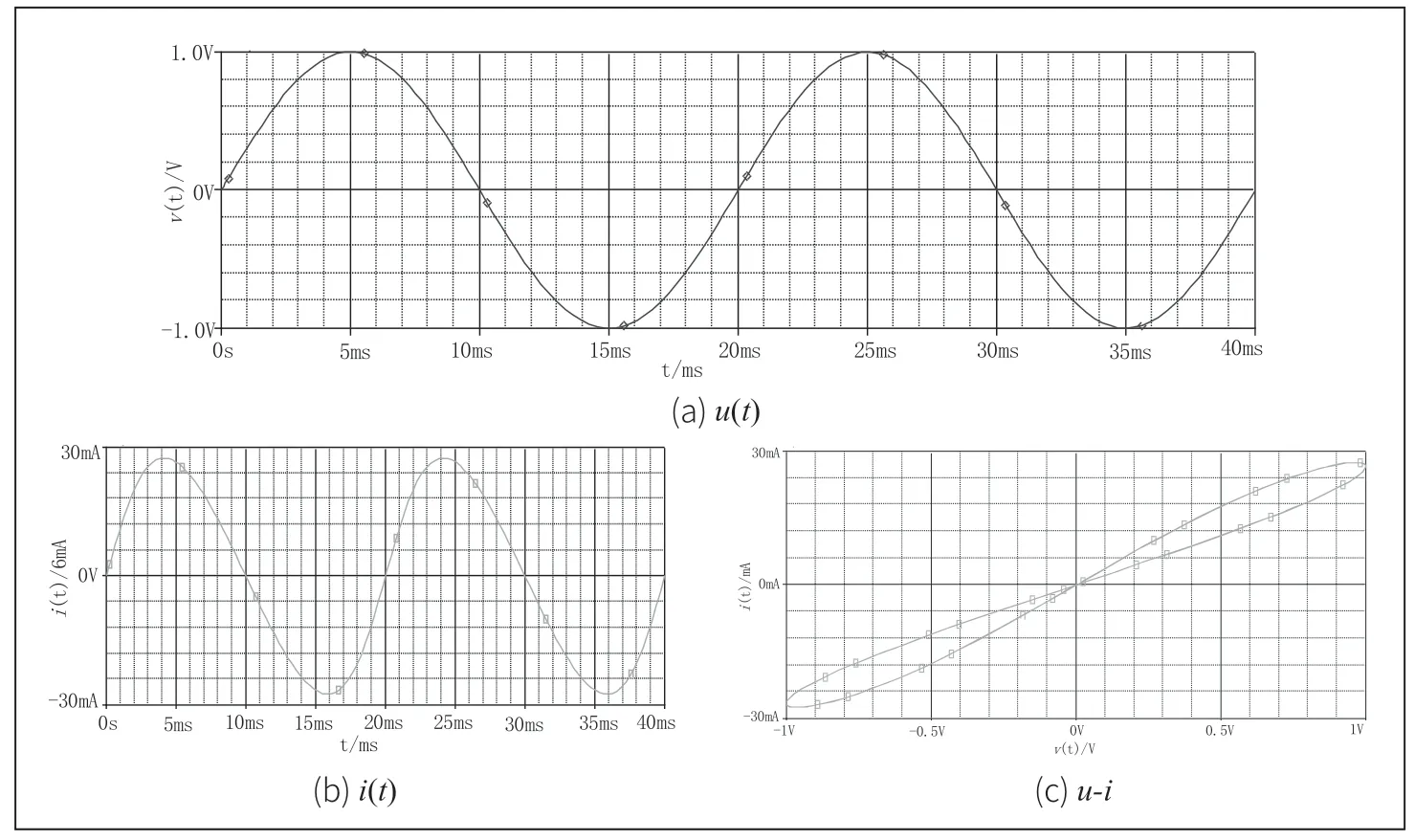
圖3 鏡像電流源荷控憶阻器的電路仿真

2 含憶阻器的Lorenz電路

2.1 Lorenz電路

文獻[9]中的傳統Lorenz電路如圖4所示。

圖4 傳統Lorenz電路

其數學模型為[9]：

(8)式 中V1，V2，V3，分別為電容C1，C2，C3的電容電壓。

2.2 Lorenz-CCM電路

Lorenz-CCM如圖5所示，先將鏡像電流源荷控憶阻器與L串聯，再與C3并聯。Lorenz-CCM混沌電路與通常的Lorenz電路相比，增加了2個動態元件：iL和q，iL是電感L的電流，q是指鏡像電流源荷控憶阻器的內部電荷。

圖5 Lorenz-CCM

由KVL定律和式（7）可知Lorenz-CCM的狀態方程為：

設x=V1，y=V2，z=V3，w=iL，k=q，

并定義非線性函數M(k)為：

則(9)式可重寫為：

所以，Lorenz-CCM是一個五維的一階微分方程，由式(11)可對Lorenz-CCM進行相應的演繹推導與MATLAB數值仿真。

2.3 混沌吸引子

選擇電路參數α=13；β=15；aq=1和bq=450，x0，y0，z0，w0，k0分別為狀態變量x，y，z，w，k的初始值。當（x0，y0，z0，w0，k0）=（0.01，0，0，0，0.013）時，Lorenz-CCM在x-y，y-z和x-z平面的投影圖分別如圖6(a)～(c)所示，由圖可知Lorenz-CCM呈現出一個雙渦卷形狀的吸引子。

圖6 Lorenz-CCM混沌吸引子

通過Jacobi法計算出Lorenz-CCM系統的Lyapunov指數為：L1=1.0223，L2=-0.0205，L3=-0.0376，L4=-17.6417，L5=-42.1998，Lyapunov維數DL=3.0546，因此，Lorenz-CCM為分數維。在y=0平面上四維龐加萊(poincare)映射z-w的相圖如圖7(a)所示，交點表現為有規律的密集點，且無法構成閉合曲線，所以Lorenz-CCM為混沌態。

x，y，z，w，k隨時間t變化的波形如圖7(b)所示，由圖7可知x，y，z，w，k隨t變化的過程是非周期性的。因此，由相軌圖、poincare映射、時域圖和Lyapunov指數以及其維數，可知Lorenz-CCM是混沌的。

圖7 poincare映射曲線和時域圖

2.4 平衡點集與穩定性

令式(11)的右邊等于零，即：

可得(12)式的平衡點集為：

從上述分析可知k軸上的點集都是平衡點，在此c為實常數。當α=13；β=15；aq=1；bq=450和k=c，(11)式在平衡點處的Jacobi矩陣JE為：

平衡點集E的特征根方程：

當令(15)式中括號的系數為：

令式（15）的根的實部小于零時，可得：

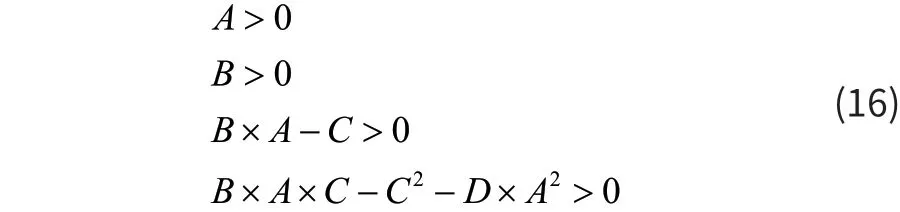
解得c＜0.00222。所以，當式（15）中c＞0.00222時，平衡點集是不穩定的。

2.5 對初始值的敏感性

當α=13，β=15，aq=1與bq= 450時。且x，y，z，w，k的初始值(x0，y0，z0，w0，k0)=(0.01，0，0，0，0.013）時，x隨時間t變化的波形如圖8所示。當x0僅相差0.000001，y0，z0，w0，k0保 持 不 變，x在t=11.8s后 截 然 不 同。當x0=0.0130001時Lorenz-CCM的Lyapunov如圖9所示，由圖9可知Lorenz-CCM有一個大于零的Lyapunov指數。因此，Lorenz-CCM是混沌的。

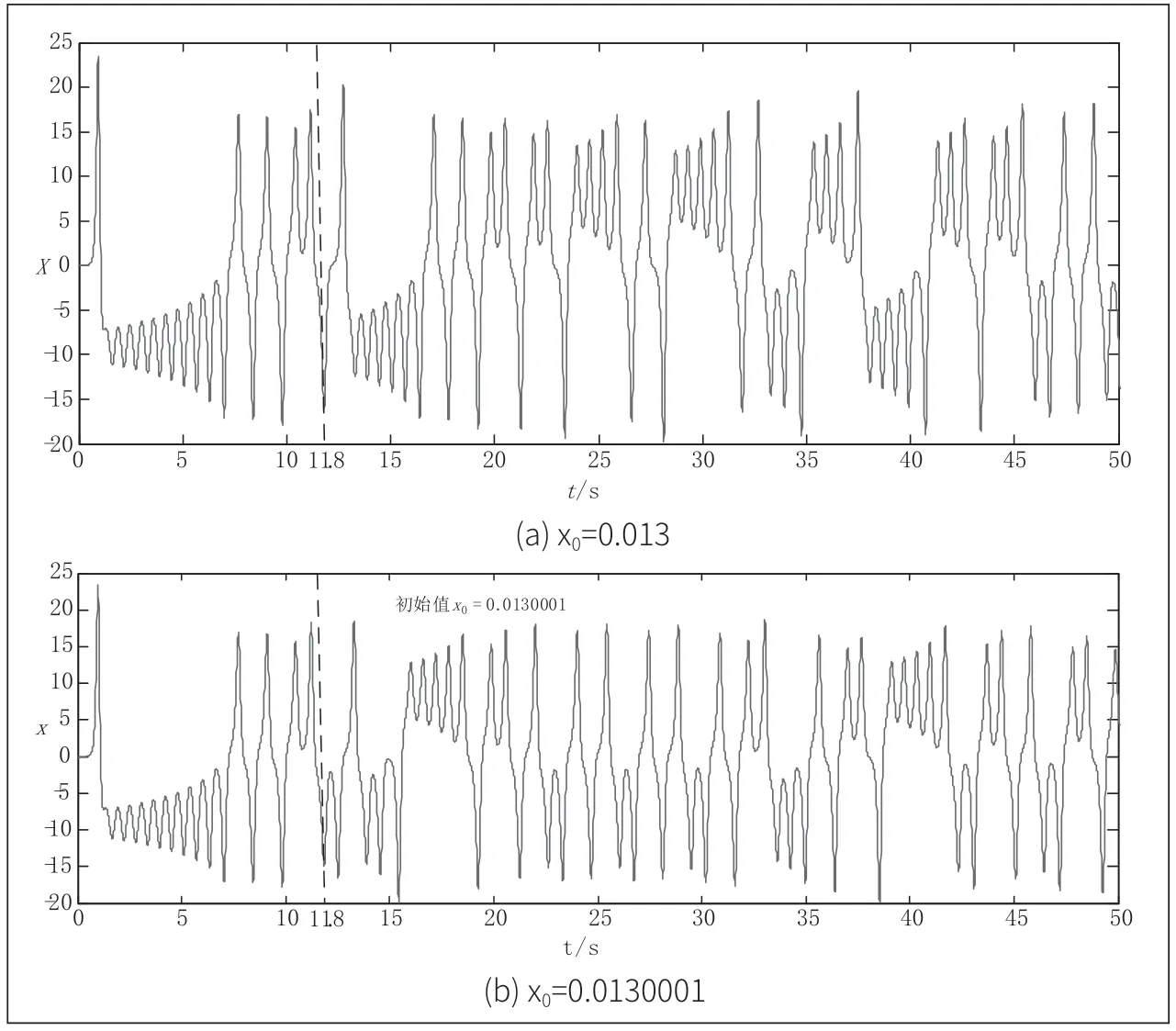
圖8 不同x0時x的時域波形

圖9 x0=0.0130001系統的Lyapunov指數譜

3 動力學分析

3.1 初始條件為（0.01，0，0，0，0.013）時，參數α變化

當β=15；aq=1和bq=450，且x，y，z，w，k的初始值(x0，y0，z0，w0，k0)=(0.01，0，0，0，0.013）時，α為可變狀態變量。利用Lyapunov指數譜、分岔圖和相軌跡圖對Lorenz-CCM進行非線性行為分析。當α增加時，最大Lyapunov指數譜和以y=0為龐加萊截面z的分岔圖分別如圖10(a)～(b)所示，對比圖10(a)和圖10(b)可知，最大Lyapunov指數與分岔圖是一致的，在α較大的變化范圍內，Lorenz-CCM是呈混沌態的。

從圖10(b)可看到Lorenz-CCM通向混沌的道路，在Lorenz-CCM混沌帶中有多個周期軌道和擬周期軌道的窗口。表2列出了α變化范圍內對應的非線性行為。

圖10 α變化時動力學行為

表2 參數α區間及其對應的非線性行為

圖11 呈現了Lorenz-CCM的周期、擬周期和混沌軌道。圖11(a)為α=2.00時，x-y呈現出的穩定原點；圖11(b)為α=4.00時，x-y呈現出的穩定極限環。圖11(c)呈現出了一個擬周期狀態；圖11(d)呈現出混沌態。

圖11 不同α時的x-y相平面

3.2 瞬態混沌現象

當α=6.71時，Lorenz-CCM出現的瞬態混沌現象[3]如圖12所示，其瞬態混沌吸引子和穩態周期極限環在x-y平面的相圖分別如圖12(a)和12(b)所示。x隨時間t變化的波形如圖12(c)所示，與通常的Lorenz不同的是，當時間在0＜t＜34s時，Lorenz-CCM是混沌狀態。當t＞34s時，Lorenz-CCM為穩定的周期態。圖12(d)為Lorenz-CCM的最大Lyapunov指數，其在一定的范圍內大于零，但是隨著t的增大而逐漸變為0。

圖12 瞬態混沌現象

4 Lorenz-CCM系統實現

由 圖7可 知，(x，y，z，w，k)的 數 值 完 全 大 于LM741、AD633的電源電壓。所以，可以將其減小一定的比例才能作為芯片的輸入，當將x，y，z，w，k同時縮小10倍時，可得：

則Lorenz-CCM可重寫為：

根據式(18)，設計出的Lorenz-CCM電路如圖5所示，其狀態方程為：

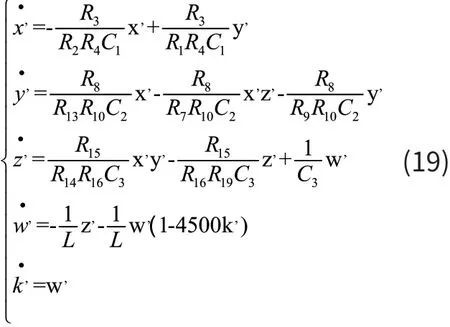
將式(18)與式 (19)比較，可得：

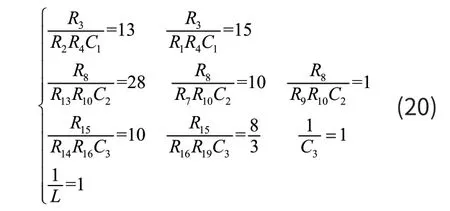
由(20)式 可 得L=1H，C3= 1F。同時當取表3的實驗參數時，再根據圖5設計的電路進行實驗。

表3 實驗參數

V1-V2、V2-V3和V1-V3的 實 驗波形分別如圖13(a)～(c)所示，將圖13(a)～(c)與圖6(a)～(c)分別對應比較后可知, 實驗結果與數值仿真結果是一致的。因此，實驗結果驗證了Lorenz-CCM理論演繹與電路設計的正確性。

圖13 Lorenz-CCM的實驗波形

5 結束語

通過本文對含荷控憶阻器混沌電路的研究可得以下結論：

(1) 基于鏡像電流源的荷控憶阻器消除了現有運放憶阻器存在的積分漂移現象。

(2) Lorenz-CCM系統和其他混沌電路類似的特點：對狀態變量初始值變化的敏感性、確定性、有界性、難以預測、大于零的最大Lyapunov指數等特點。

(3) 與通常的Lorenz電路相比，Lorenz-CCM存在瞬態混沌現象且易于硬件電路實現，可在應用于各種保密工程中。