基于線性回歸的單柱塞泵單向閥參數優化

米 鑫，李 虹，郭彥青，高宏偉，王浩楠，寧羿帆

（1.中北大學機械工程學院，山西太原 030051；2.陜西晟思智能測控有限公司，陜西西安 710100）

單柱塞泵具有容積效率高、壓力脈動小和流量調節方便等優點，被廣泛應用于車輛工程、農業機械和航空航天等領域[1-2]。單柱塞泵通常采用閥配流方式，閥配流主要依靠單向閥實現，即在柱塞腔的進、出油口分別安裝單向閥。單向閥是單柱塞泵系統中最核心的元件，其性能直接影響整個系統的性能。

近年來，國內外針對影響單向閥性能的參數進行了大量研究。例如：陶柳等人[3-4]基于AMESim軟件，通過仿真分析了彈簧剛度、閥芯質量和液動力對單向閥動態穩定性的影響。姚麗英等人[5]研究了閥芯活塞桿直徑對FDY480/50型液控單向閥開啟壓力的影響。常玉連等人[6]利用Fluent軟件中的動網格技術研究了彈簧剛度對單向閥開啟過程的影響。李勝永[7]通過建立球型單向閥的性能優化模型，并利用序列二次規劃方法對其閥芯直徑、閥座通徑等參數進行了優化。Woo等人[8]研究了閥門剛度對壓電往復泵流量和壓力的影響。Xing等人[9]通過建立抽油泵的動力學模型，研究了影響泵效率的性能參數。綜上可知，目前圍繞單柱塞泵系統中配流單向閥的研究主要以單一參數對單向閥性能的影響以及運動學仿真分析為主。但是，單向閥的設計牽涉因素較多，且各因素之間聯系緊密，用傳統方法設計的單向閥雖能滿足使用要求，但其參數不一定是最合理的，會造成吸油不充分、系統響應慢等問題。

上述研究表明，利用仿真軟件開展運動學分析，并將仿真結果與數學模型相結合，可以很好地解決單向閥參數設計不合理問題。基于此，筆者提出將線性回歸模型應用于單向閥參數優化。首先，基于AMESim軟件開展單柱塞泵系統仿真分析，并利用MATLAB擬合工具箱求解單向閥參數（彈簧預緊力、彈簧剛度和閥芯質量）與進油口流量的關系；然后，利用主成分分析法消除各參數之間的相關性，并以進油口流量為因變量、各參數為自變量、各參數的取值范圍為約束條件，基于線性回歸構建單向閥參數優化模型；接著，以進油口流量最大為優化目標，采用遺傳算法對各參數進行優化求解；最后，通過仿真分析和實驗來驗證所提出方法的有效性。

1 單柱塞泵系統中單向閥參數與進油口流量的關系分析

1.1 單柱塞泵

本文所研究的單柱塞泵的結構如圖1所示，主要由主軸、斜盤、柱塞、缸體、進油口和出油口等組成，其中進油口和出油口分別連接單向閥。單柱塞泵的主要尺寸如圖2所示：斜盤傾斜17°；柱塞直徑為34 mm，柱塞分布圓直徑為129 mm，柱塞的最大行程為39.4 mm；缸體外徑為179 mm，缸體長度為128 mm。

圖1 單柱塞泵結構示意Fig.1 Schematic diagram of single plunger pump

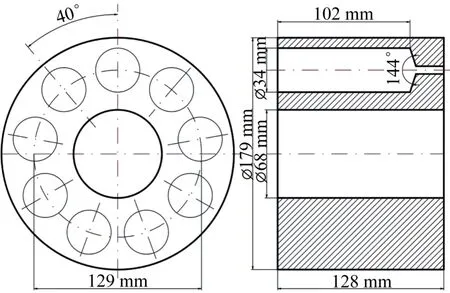
圖2 單柱塞泵的主要尺寸Fig.2 Main dimensions of single plunger pump

圖1所示單柱塞泵的工作原理如下：在原動機驅動下，主軸旋轉并帶動斜盤轉動，缸體固定。由于斜盤的作用，當柱塞向左作伸出運動時，進油口單向閥開啟，出油口單向閥反向截止，油液從進油口進入柱塞腔；當柱塞向右作壓縮運動時，出油口單向閥開啟，進油口單向閥反向截止，油液從出油口排出[10]。

1.2 單向閥參數與進油口流量的定量關系

單向閥閥芯的動力學方程如下[11]：

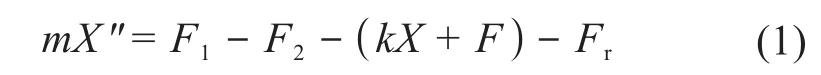
式中：m為閥芯質量；X為閥芯位移；F1為閥芯所受的液壓力；F2為閥芯所受的液動力；k為彈簧剛度；F為彈簧預緊力；Fr為閥芯與閥座間的黏性阻力和摩擦阻力。

由閥芯的動力學方程可知，影響單向閥性能的主要參數為彈簧預緊力F、彈簧剛度k和閥芯質量m。為了準確地描述單向閥的工作狀態，根據液壓原理在AMESim軟件中搭建單柱塞泵系統并進行仿真分析，如圖3所示（圖中：φ、θ、J、T、ω、ν、Fp和M分別為單柱塞泵的斜盤傾角、轉角、轉動慣量、轉矩、角速度、速度、力和質量）。設置單柱塞泵的轉速為1 000 r/min且呈正弦變化；單向閥閥芯的位移為0～0.005 m。

圖3 單柱塞泵系統仿真模型Fig.3 Simulation model of single plunger pump system

單向閥的性能難以直接測量，可通過測量單柱塞泵進油口流量來間接反映單向閥的性能。采用控制變量法，基于圖3所示的單柱塞泵系統開展仿真分析，分別探討單向閥的彈簧預緊力F、彈簧剛度k和閥芯質量m與進油口流量q之間的定量關系。

1.2.1 彈簧預緊力與進油口流量

在仿真分析中，取彈簧剛度k=0 N/mm、閥芯質量m=0.05 kg，令彈簧預緊力F從0 N逐漸開始增大至23 N（以1 N為間隔），觀察單向閥的閥芯位移變化曲線，并記錄單柱塞泵的進油口流量。結果表明：當8≤F≤23 N時，單向閥閥芯的最大位移能達到預先設定的0.005 m，閥芯開啟時間與關閉時間大致相等，滿足設計要求；當F＜8 N時，雖然單向閥的閥芯可以達到預先設定的0.005 m，但是其在1個運動周期內一直處于開啟狀態，不滿足設計要求。

利用MATLAB擬合工具箱將上述滿足設計要求的單向閥彈簧預緊力F與單柱塞泵進油口流量q（平均流量，下文同）的仿真數據進行曲線擬合，結果如圖4所示。

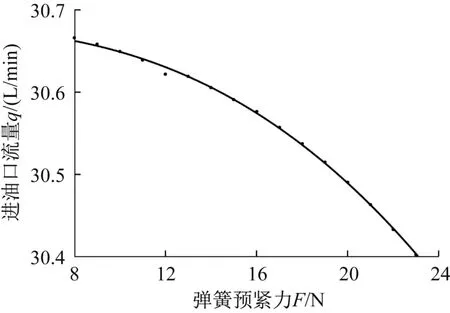
圖4 進油口流量與彈簧預緊力的關系曲線Fig.4 Relation curve between oil inlet flow and spring pretightening force

根據圖4所示擬合結果，進油口流量q與彈簧預緊力F的定量關系可表示為：

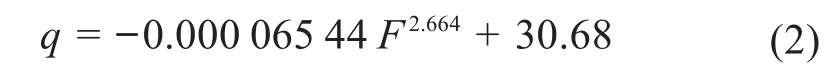
1.2.2 彈簧剛度與進油口流量

在仿真分析中，取彈簧預緊力F=0 N、閥芯質量m=0.05 kg，令彈簧剛度k從0 N/mm逐漸開始增大（以1 N/mm為間隔），觀察單向閥的閥芯位移變化曲線，并記錄單柱塞泵的進油口流量。結果表明：當5≤k≤17 N/mm時，單向閥閥芯的最大位移能達到預先設定的0.005 m，閥芯開啟時間和關閉時間大致相等，滿足設計要求；當k＞17 N/mm時，雖然閥芯可以達到預先設定的0.005 m，但單柱塞泵系統響應慢且吸油不充分，不滿足設計要求。

利用MATLAB擬合工具箱將上述滿足設計要求的單向閥彈簧剛度k與單柱塞泵進油口流量q的仿真數據進行曲線擬合，結果如圖5所示。

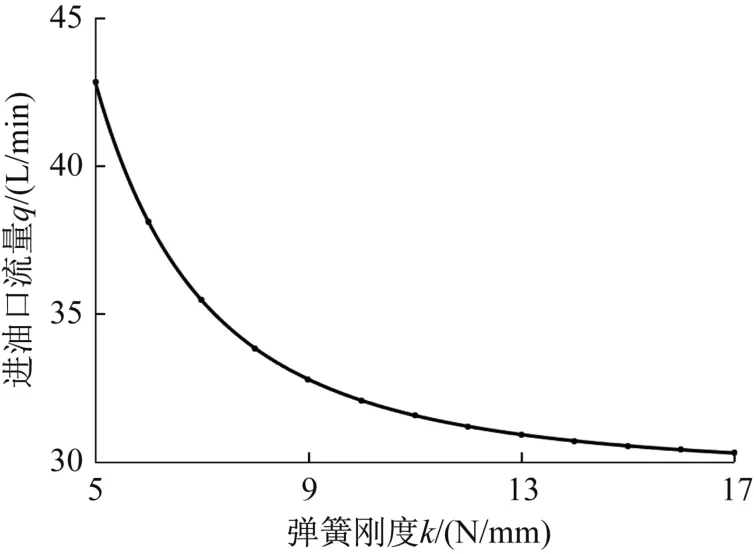
圖5 進油口流量與彈簧剛度的關系曲線Fig.5 Relation curve between oil inlet flow and spring stiffness

根據圖5所示的擬合結果，進油口流量q與彈簧剛度k的定量關系可表示為：

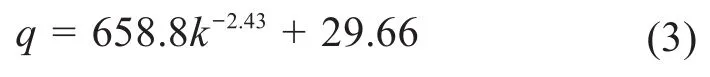
1.2.3 閥芯質量與進油口流量

不同質量閥芯的結構不變，但閥口面積隨質量的增大而增大。在實際應用中，單向閥的質量為幾十克到幾百克，本文主要以閥芯質量為0.01～0.10 kg的單向閥為研究對象。在仿真分析中，取彈簧預緊力F=0 N、彈簧剛度k=0 N/mm，改變閥芯質量m（以0.01 kg為間隔），觀察單向閥的閥芯位移變化曲線，并記錄單柱塞泵的進油口流量。結果表明：當0.01≤m≤0.10 kg時，單向閥閥芯的最大位移能達到預先設定的0.005 m，吸油充分，閥芯的開啟時間和關閉時間大致相等，滿足設計要求。

利用MATLAB擬合工具箱將上述滿足設計要求的單向閥閥芯質量m與單柱塞泵進油口流量q的仿真數據進行曲線擬合，結果如圖6所示。

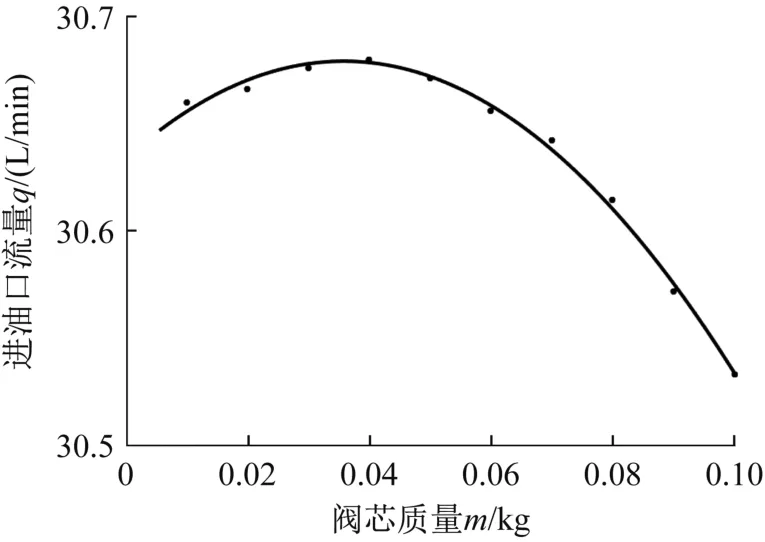
圖6 進油口流量與閥芯質量的關系曲線Fig.6 Relation curve between oil inlet flow and valve core mass

根據圖6所示擬合結果，進油口流量q與閥芯質量m的定量關系可表示為：

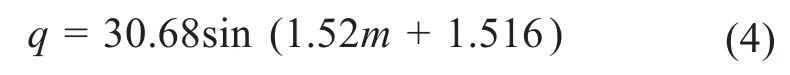
綜合上述仿真結果可知，單向閥的彈簧預緊力、彈簧剛度和閥芯質量共同影響了單柱塞泵進油口流量，但這3個參數彼此間存在相關性，故單純的動力學分析難以進行參數優化。

2 基于線性回歸的單向閥參數優化模型

由式(2)至式(4)可知，進油口流量q與F2.664、k-2.43、sin(1.52m+1.516)均呈線性關系。令a1=F2.664、a2=k-2.43、a3=sin(1.52m+1.516)，則q與a1、a2、a3均呈線性關系。忽略其他參數對單向閥性能的影響，采用主成分分析消除彈簧預緊力、彈簧剛度、閥芯質量之間的相關性，并基于線性回歸建立單向閥參數優化模型。

2.1 主成分分析

主成分分析是一種在高維歐氏空間中對給定數據集進行降維的方法[12]，通過降維可以消除原始數據的相關性。該方法通過構造一系列線性組合來形成一組新的互不相關的變量，且保證這些新變量盡可能多地反映原變量的信息。同時改變彈簧預緊力F、彈簧剛度k和閥芯質量m這3個參數，在AMESim軟件中對圖3所示的單柱塞泵系統進行仿真，觀察單向閥閥芯位移和速度的變化曲線，并記錄單柱塞泵的進油口流量。基于選取的3個參數的值，利用式(2)至式(4)計算a1、a2、a3；然后，采用主成分分析計算a1、a2、a3對應的特征值，分別為2.561 6，0.437 5和0.000 9，其對應的特征向量如下：

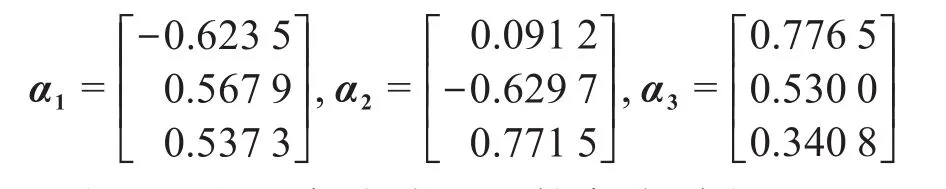
由此可得，各成分的貢獻率分別為85.386%，14.582%，0.032%。本文選取累計貢獻率達到90%以上的成分（即前2個成分）作為主成分，記為W1、W2。根據表1數據可得W1、W2與a1、a2、a3的關系：

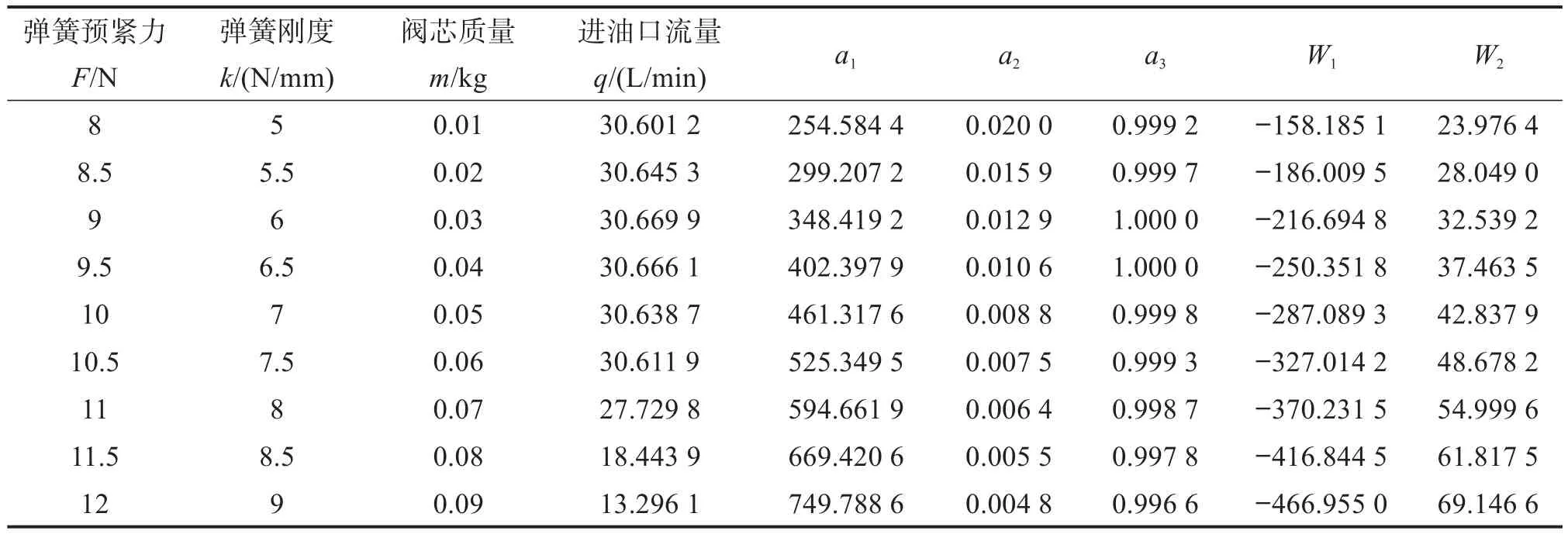
表1 單向閥參數的主成分分析結果Table 1 Principal component analysis results of check valve parameters

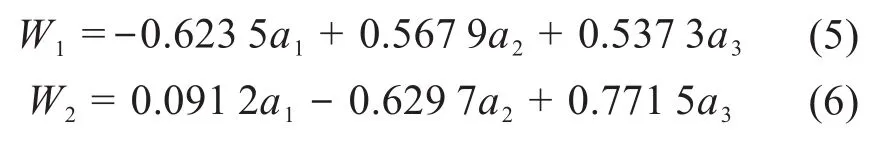
2.2 單向閥參數優化模型

若因變量同時受到n個自變量的影響，且這n個自變量皆與因變量呈線性關系并彼此不相關，則這n+1個變量就形成了n元線性回歸[13]。根據上文分析可知，進油口流量q與主成分W1、W2均呈線性關系，且W1、W2不相關。基于此構建線性回歸模型，即：

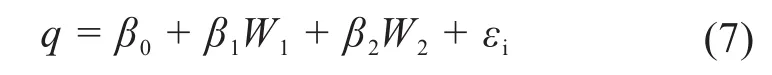
式中：β0為回歸截距；β1、β2為偏回歸系數；εi為誤差。

根據表1所示的q、W1、W2，在MATLAB擬合工具箱中對線性回歸方程(7)進行求解，得到進油口流量擬合值與實際值的對比結果，如圖7所示。根據擬合結果，得到所構建線性回歸模型中各參數的值分別為β0=-561.955 3，β1=104.280 4，β2=712.682 5。代入式(7)可得：

圖7 進油口流量實際值與擬合值對比Fig.7 Comparison between actual value and fitting value of oil inlet flow

線性回歸模型能否真實地反映因變量與自變量之間的相關關系，需要進行隨機誤差和顯著性的檢驗。隨機誤差可用相關系數r2來表示，顯著性水平用統計量T表示。通過MATLAB擬合工具箱求得所構建線性回歸模型的統計量：r2=0.979 6、T=123.072 4、P=0.000 0。根據計算結果可知，相關系數r2接近1，說明隨機誤差小，所構建線性回歸模型符合實際；統計量T較大，其對應的概率P＜0.05，說明所構建線性回歸模型顯著。

若相關變量超出合理范圍，則系統將失穩[14]。故將彈簧預緊力、彈簧剛度、閥芯質量的取值范圍作為約束條件，以進油口流量q為因變量，各參數為自變量，構建單向閥參數優化模型：

通過構建線性回歸模型，將單向閥的參數優化問題轉化為求解非線性函數的最大值問題。由于本文所構建的優化模型具有非線性特點，且不單求解一個參數，常規計算方法的難度較大。相對于一般的優化方法，利用遺傳算法解決多參數優化問題，可以避免陷入局部最優解，提高計算精度。

3 基于遺傳算法的單向閥參數優化求解及仿真分析

3.1 基于遺傳算法的單向閥參數優化求解

遺傳算法是一種借鑒生物界自然選擇和遺傳機制的隨機搜索算法，其在液壓伺服系統優化中得到了廣泛應用[15]。基于上文所構建的單向閥參數優化模型，利用遺傳算法進行優化求解，具體思路如下：將彈簧預緊力、彈簧剛度和閥芯質量的可能解看作群體中的染色體并采用實數編碼[16]，模擬自然界中的選擇、交叉、變異；然后按照進油口流量函數對每個個體的適應度進行評價，在全局內進行最優個體搜索。基于遺傳算法的參數優化求解技術路線如圖8所示。

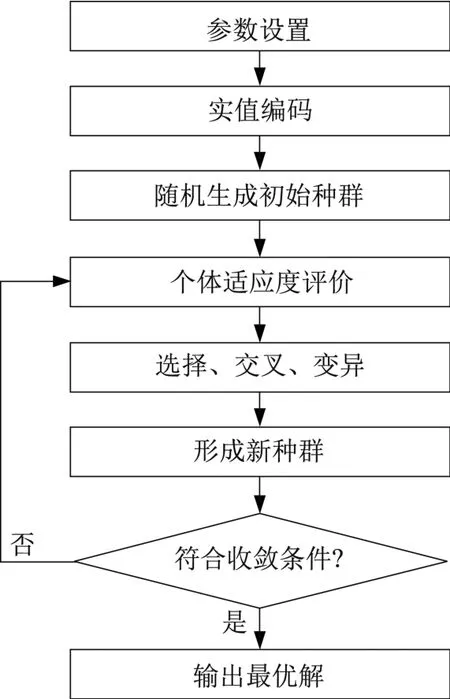
圖8 基于遺傳算法的參數優化求解技術路線Fig.8 Technical route of parameter optimization based on genetic algorithm

1）參數設定。

設種群大小N=50，交叉率Pc=1，變異率Pm=0.01。

2）編碼。

因涉及3個參數的優化求解，故每個染色體中含3種基因，采用實數對3種基因進行編碼。

3）初始種群生成。

由于遺傳的需要，必須提前設定初始種群。為了保證生物的多樣性和競爭的公平性，通過隨機方法生成。

4）個體適應度函數確定。

遺傳算法是在全局內尋找最小解，故適應度函數需要對目標函數q進行取反處理，即：

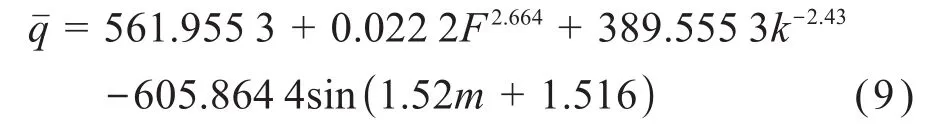
5）選擇、交叉、變異。

選擇運算采用賭輪盤方式，根據每個個體在種群中的適應度來確定個體是被保留還是淘汰；交叉運算采用中間重組算子；變異運算采用非均勻突變算子[17]。

6）收斂條件設置。

當種群中最優個體間的適應度誤差小于0.000 1時，迭代結束。

基于遺傳算法的進油口流量迭代曲線如圖9所示。由圖可知，當種群迭代111次后滿足收斂條件，此時最大的進油口流量為37.858 7 L/min，對應的單向閥參數為：F=8 N，k=16.99 N/mm，m=0.036 kg。

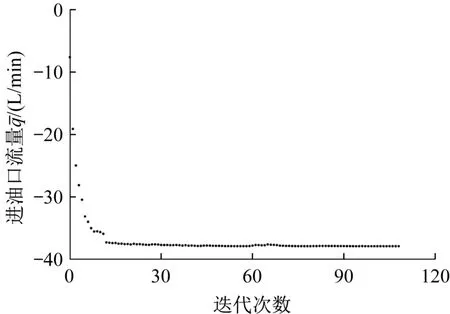
圖9 基于遺傳算法的進油口流量迭代曲線Fig.9 Iterative curve of oil inlet flow based on genetic algorithm

3.2 優化后單向閥仿真分析

為了驗證所提出單向閥參數優化方法的有效性，基于優化前最大進油口流量對應的參數F=9 N、k=6 N/mm、m=0.03 kg和優化后的參數F=8 N、k=16.99 N/mm、m=0.036 kg，分別搭建如圖3所示的單柱塞泵系統仿真模型。其中，單柱塞泵和進油、排油單向閥均采用HCD庫中的元件進行搭建，且2個單向閥的其余參數完全一樣；泵出口采用溢流閥進行負載模擬加載。

圖10所示為優化前后單柱塞泵進油口流量（瞬時流量）的變化曲線。由圖可知，優化后進油口流量為37.206 2 L/min，而優化前最大的進油口流量為30.669 9 L/min；對比優化前，優化后的進油口流量提升了21.3%。

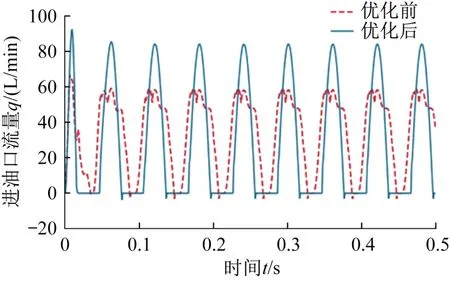
圖10 優化前后進油口流量對比Fig.10 Comparison of oil inlet flow before and after optimization

對比優化前，優化后單柱塞泵進油口的流量更大，吸油更充分；當流量曲線趨于穩定后，閥芯開啟時沒有脈動，整體更平滑，且曲線接近于正弦曲線的上半部分，滿足單柱塞泵配流的設計要求。

圖11所示為優化前后單向閥閥芯位移變化曲線。從圖中可以看出：優化前單向閥的彈簧剛度較小，導致單向閥以較大的速度快速到達最大位移處，且換向時對閥芯底座的沖擊力大；閥芯長時間處于開啟狀態，開啟時間遠大于關閉時間，不滿足單柱塞泵配流的設計要求。優化后單向閥緩慢地到達最大位移處，對閥芯底座的沖擊小；吸油時單向閥閥芯緩慢開啟至最大，隨后又緩慢關閉，基本符合正弦運動規律，且吸油和關閉的時間基本相同，滿足單柱塞泵配流的設計要求。

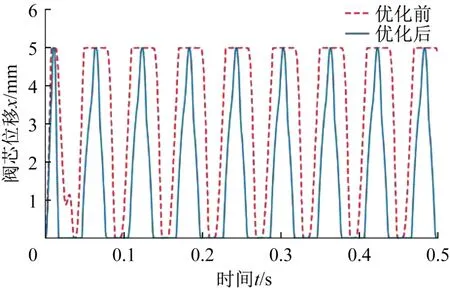
圖11 優化前后單向閥閥芯位移對比Fig.11 Comparison of check valve core displacement before and after optimization

結合圖10和圖11可以發現：優化前單向閥閥芯雖然開啟時間長，但在吸油時排油單向閥也處于開啟狀態，導致一部分油液直接從進油口流向了排油口，并沒有流入單柱塞泵。此外，由于優化前進、出油口單向閥同時開啟，雖然其閥芯位移可達到最大，但實際流量卻不再增加。

綜上所述，優化前單向閥彈簧剛度較小，導致單向閥并不能完全滿足單柱塞泵的配流要求。優化后單向閥基本滿足單柱塞泵的配流要求，且吸油更充分，運行更平穩。

4 實驗驗證

為了進一步驗證上述單向閥參數優化方法的有效性，以不同參數的RC型單向閥為研究對象，通過測量單柱塞泵進油口流量進行對比分析。搭建圖12所示的單柱塞泵系統實驗裝置，主要由伺服電機、轉速扭矩傳感器、單柱塞泵、單向閥和流量計組成。單柱塞泵的轉速由伺服電機提供，配置轉速扭矩傳感器測量泵的轉速和扭矩，配置流量計測量進油口流量，所選傳感器的參數如表2所示。優化前，選用的單向閥為RC14；優化后，選用的單向閥為RC32，2種單向閥的區別如表3所示。圖12中有4個單向閥，本實驗只用其中2個，另外2個用堵頭堵住；實驗所用的單向閥安裝在特殊加工的閥體中，不同型號的單向閥安裝尺寸不同，更換單向閥需要將整個閥體拆卸安裝。實驗溫度為(50±4)℃，運動黏度為42～74 mm2/s，單柱塞泵的轉速為1 000 r/min。

圖12 單柱塞泵系統實驗裝置Fig.12 Experimental device of single plunger pump system

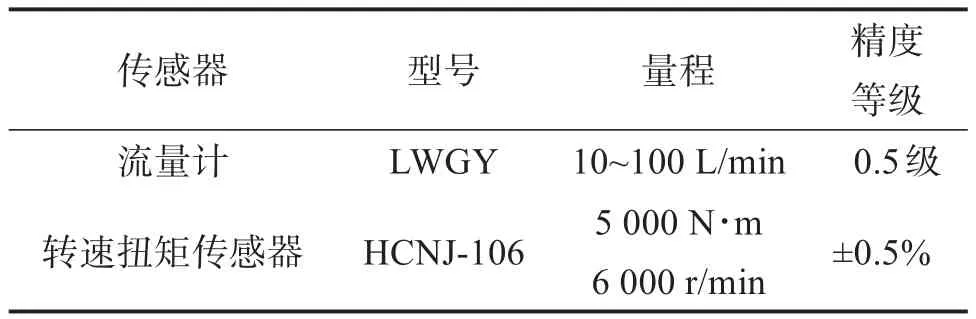
表2 實驗用傳感器參數Table 2 Parameters of sensor for experiment

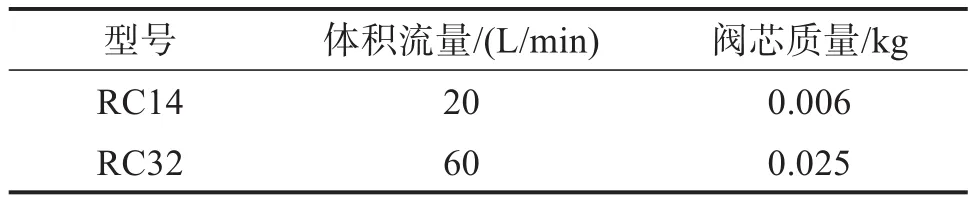
表3 不同型號單向閥的參數Table 3 Parameters of different types of check valves

利用所搭建的實驗裝置，測量優化前后單柱塞泵的進油口流量，結果如表4所示。從實驗結果可知，優化后進油口的實際流量比優化前提高了16.8%，單向閥吸油更充分，且效率更高。

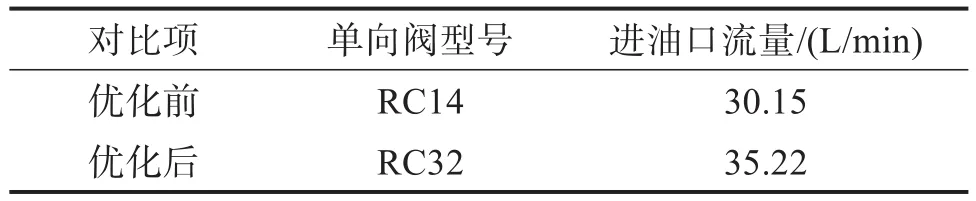
表4 優化前后進油口實際流量對比Table 4 Comparison of actual oil inlet flow before and after optimization

5 結 論

本文提出了一種基于線性回歸的單向閥參數優化方法。首先，利用AMESim軟件，通過仿真定量分析了單向閥彈簧預緊力、彈簧剛度、閥芯質量與進油口流量的關系；然后，利用主成分分析法消除了各參數之間的相關性，基于線性回歸構建單向閥參數優化模型并采用遺傳算法進行了優化求解；最后，根據優化前后的單向閥參數，通過仿真分析和實驗驗證了所提出方法的有效性。仿真和實驗結果表明：優化后進油口流量提高了15%以上，說明本文方法可為單柱塞泵系統中配流單向閥的參數優化提供理論依據。