基于GWO-SVR的深海采礦海試區海浪高度預測①
姚汭成,龔德文
(長沙礦冶研究院有限責任公司 深海礦產資源開發利用國家重點實驗室,湖南 長沙 410012)
對深海采礦海試來說,惡劣的海況可能導致試驗無法進行,甚至危及人員和設備的安全,海浪高度的準確預測對深海采礦工程具有重要意義。隨著對海浪高度預測方法的研究不斷深入,機器學習[1]及深度學習[2]中很多算法已在海浪高度預測中得到應用。
支持向量回歸[3](SVR)的原理基于支持向量機[4](SVM),是一種可靠且準確的機器學習算法。目前,使用SVR及SVM對海浪高度預測已有初步研究,但對于這兩種算法在此方面的特征構建及參數優化尚無確切方法[5-8]。
本文首次將灰狼優化(GWO)[9]和支持向量回歸算法(SVR)相結合應用于海浪高度預測。本文數據源為ERA5再分析數據[10],使用GWO算法優化SVR參數,并將GWO-SVR預測效果與傳統SVR預測效果對比,驗證GWO-SVR算法預測海浪高度的有效性;并進一步將GWO-SVR預測效果與基于粒子群算法(PSO)的PSO-SVR預測結果進行對比,驗證GWO-SVR算法預測的準確性。最后,據現有研究成果,建立了3種海浪高度預測數據模型構建算法輸入特征,并用GWO-SVR算法預測海浪高度。3種數據模型預測結果證實,使用較大空間范圍的海洋環境數據構建特征訓練算法可明顯減少預測誤差。
1 數據選擇及預測點
本文預測區域為某深海采礦海試區域,區域中心位置為115.5°E,預測點在18.5°N(見圖1),此處離海岸較遠,涌浪的影響不容忽視。本文數據源為ERA5再分析數據,其數據類型有:有效波高(SWH)、10 m風速U(U10)和V(V10)分量、2 m溫度(T2M)、海面氣壓(MSL)、實際云量(TCC);數據的時間分辨率為1 h、空間分辨率為0.5°×0.5°,時間區間從2020年1月1日至2020年12月31日。
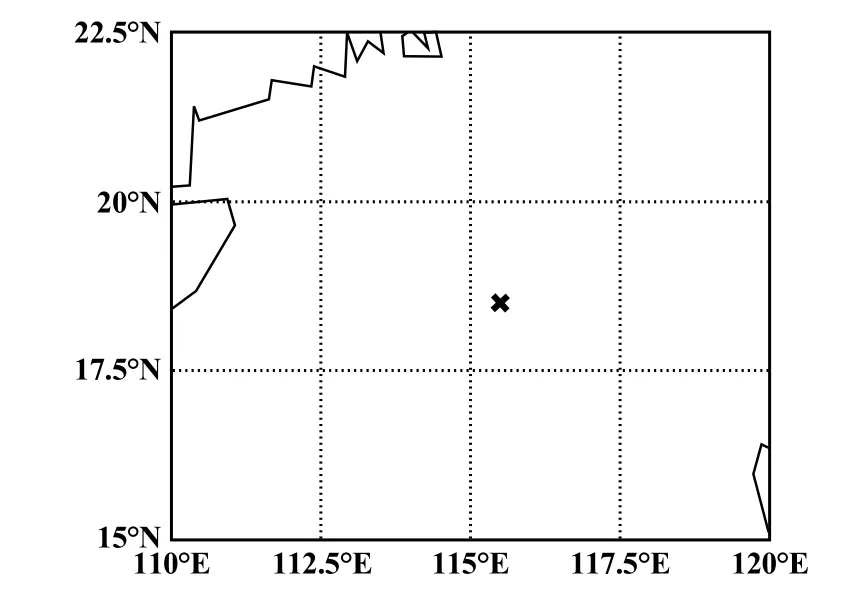
圖1 預測點選擇
2 GWO-SVR算法構建
灰狼優化算法的優化過程基于狼群的社會等級和捕食行為。如圖2所示,根據狼群社會等級關系,將每代適應度最好的3個個體分別標記為α、β、δ,剩下的個體標記為ω。其優化過程由每代適應度最好的3個解指導完成。而SVR的原理基于SVM,可使用核函數將線性SVR擴展為非線性SVR,使其可以進行非線性的回歸預測。
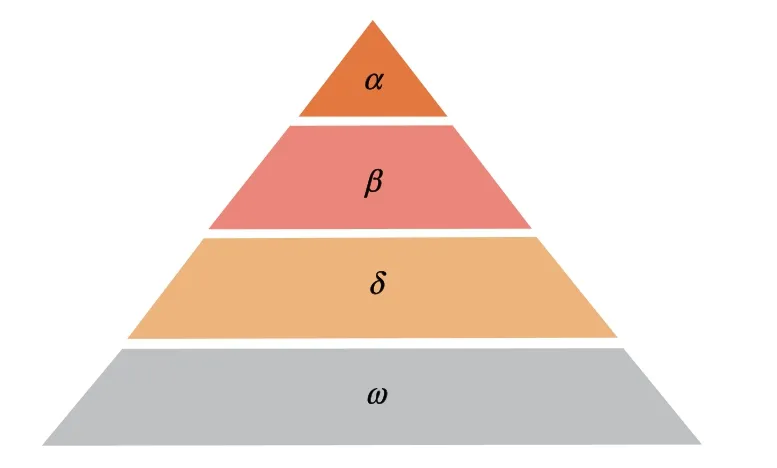
圖2 狼群社群等級關系
2.1 GWO-SVR算法
本文使用基于高斯核函數非線性SVR預測海浪高度,要確定的參數包括懲罰系數C、合理誤差ε和高斯核函數寬度參數γ,目前該算法參數尋優困難,本文使用GWO算法優化SVR參數。GWO-SVR算法實現步驟如下:
1)數據預處理:輸入數據歸一化,采用式(1)對輸入數據進行預處理:

式中xscaled為標準化后的輸入數據;x為原始輸入數據;x為輸入數據均值;xstd為輸入數據標準差;
2)分割數據集:將數據集按照1∶3的比例分為測試集和訓練集;
3)設置GWO-SVR參數:設置狼群數量Pack_size、迭代次數Iterations、參數上界max_values和下界min_values;
4)適應度定義:如式(2)所示,使用實際浪高和預測浪高的均方誤差MSE作為GWO-SVR算法適應度函數:
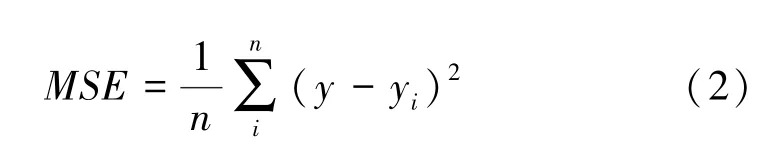
5)構建GWO-SVR算法:使用Python語言構建GWO算法,并通過scikit-learn工具包將C、ε和γ參數帶入SVR迭代訓練。
算法的執行流程如圖3所示。
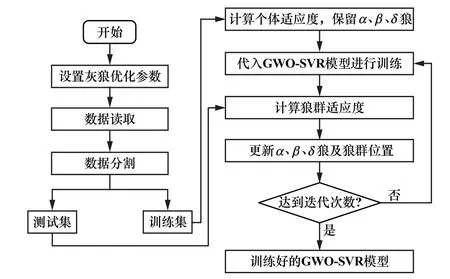
圖3 GWO-SVR算法流程
2.2 評估標準
本文使用均方根誤差RMSE、平均絕對誤差MAE和平均絕對百分比誤差MAPE作為算法預測效果評估標準,RMSE、MAE、MAPE值越小,算法預測效果就越好。
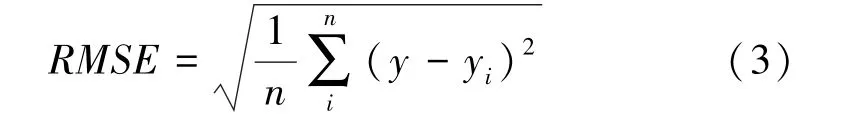
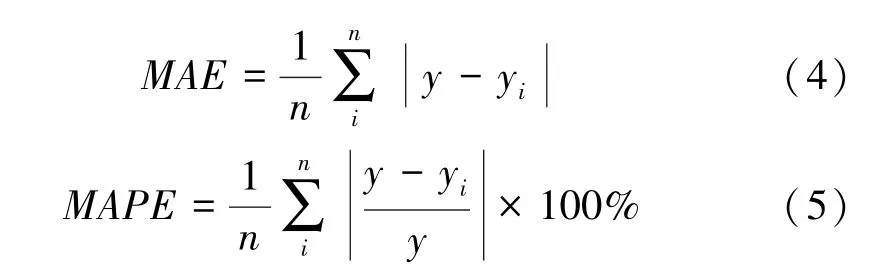
式(2)~(5)中y為實際有效波高;yi為預測有效波高。
3 基于GWO-SVR深海采礦海試區有效波高預測
3.1 算法輸入特征構建
基于Python 3.8的環境下完成GWO-SVR算法構建。海浪一般分為風浪和涌浪。風浪是受當地風影響的波浪。當波浪從其產生地傳播出去,或其相速度超過當地風速時,就被稱作涌浪。所以,在SVR特征構建時,不僅要考慮預測點受到風影響產生的風浪,還要考慮預測點受到環境因素產生涌浪的影響,更要考慮周圍各點海洋環境對預測點海浪高度的影響。因此,本文選擇有效波高(SWH)作為預測對象。
為進一步提高算法對海浪高度的預測能力,深入探究周圍環境及海浪狀態對預測點有效波高預測的影響,構建了M0、M1和M2共3種數據點空間分布模型構建算法輸入特征。M0數據點數據僅為預測點當前時刻的海洋環境參數;M1數據點數據為預測點當前時刻的海洋環境參數及距預測點經緯度0.5°×0.5°內各數據點的海洋環境參數;M1數據點數據為預測點當前時刻的海洋環境參數及距預測點經緯度1.0°×1.0°內各數據點的海洋環境參數。上述海洋環境參數包括:數據點當前有效波高、10 m風速U和V分量、2 m溫度、海面氣壓及實際云量。數據點分布如圖4所示。
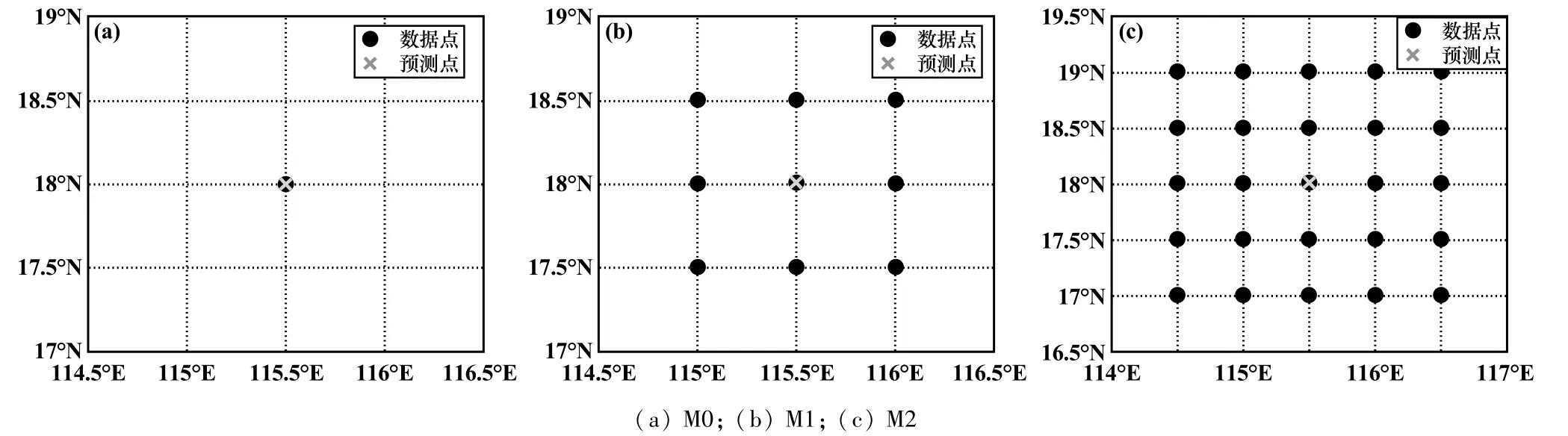
圖4 數據點分布模型
3.2 算法訓練及預測
通過大量預試驗調整GWO-SVR算法初始參數范圍,當GWO-SVR算法參數狼群個體數pack_size=10、最大迭代次數iterations=60、參數下界min_value=0.000 1、參數上界max_value=10 000.000 0時,預測效果較好。然后使用訓練集數據對傳統非線性SVR(C=1,GWO-SVR和PSO-SVR進行訓練,再使用測試集計算MSE、MAE、MAPE得到各算法的預測效果,如表1~3所示。
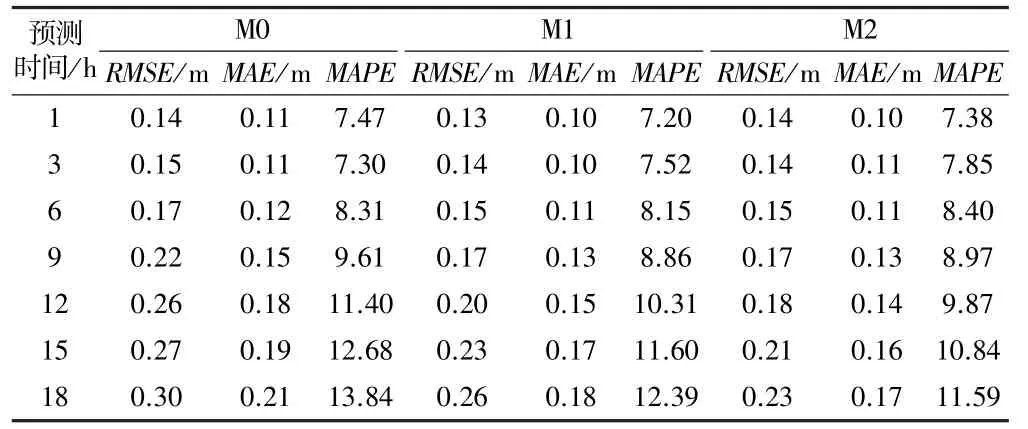
表1 傳統SVR算法預測效果
對比表1和表2數據可知:傳統SVR預測效果不佳,難以預測模型有效波高,預測誤差較大。取相同數據模型使用GWO-SVR進行預測時,其RMSE、MAE、MAPE值均小于傳統SVR方法。
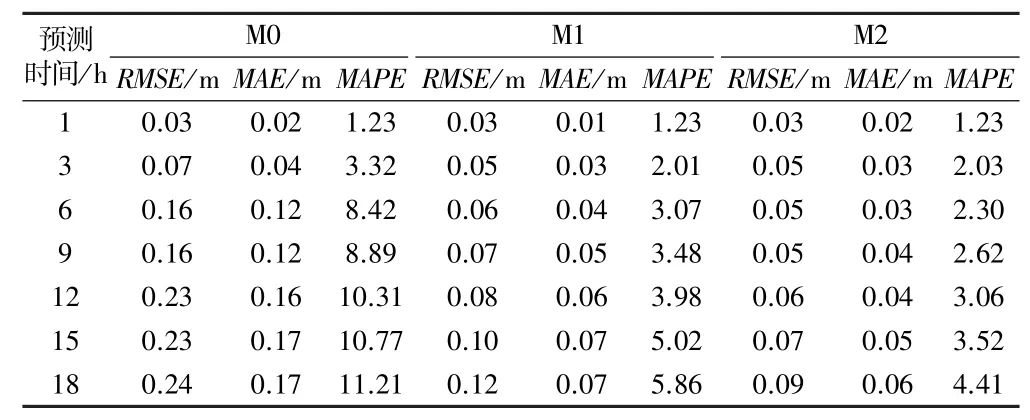
表2 GWO-SVR算法預測效果
對比表2和表3數據可知,GWO-SVR方法RMSE和MAE均比PSO-SVR方法小。如選擇數據模型M2預測時間12 h的試驗,GWO-SVR方法得到的RMSE約為PSO-SVR方法的85.7%,MAE值約為PSO-SVR方法的80%。所以GWO-SVR方法的誤差相比于PSO-SVR有一定減少。又如數據模型M2預測時間15 h以及數據模型M0預測時間1 h試驗,PSO算法在逐代優化SVR參數過程中易陷入局部最優,致使預測誤差較大。

表3 PSO-SVR算法預測效果
通過對表1~3研究及通過對GWO-SVR算法的預測結果比較可以看出,GWO-SVR算法的M0模型對有效波高預測能力較低,預測時間6 h時RMSE=0.16、MAE=0.12,失去6 h后有效波高預測能力;M1模型對有效波高的預測能力較強,預測時間12 h時RMSE升至0.16、MAE升至0.12,12 h后有效波高預測能力不佳;M2模型對有效波高預測能力強,預測時間15 h時RMSE升至0.16、MAE升至0.12,15 h后有效波高預測能力不佳。M2數據模型SVR參數優化結果如表4所示。

表4 GWO-SVR算法M2數據模型參數優化結果
根據表4優化后的C、ε、γ參數,使用訓練好的GWO-SVR算法對2021年1月該點的有效波高進行預測,未來3、6、9、12 h預測結果和實際有效波高的比對如圖5所示。
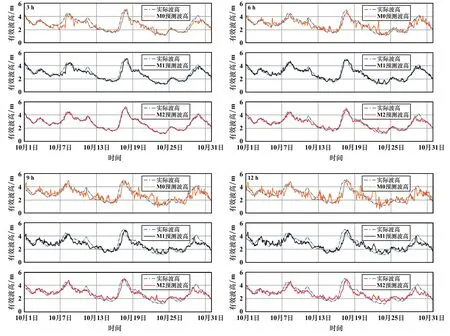
圖5 GWO-SVR有效波高預測結果
由圖5可知,未來3 h波高預測結果中,3種數據模型預測能力均表現較好,預測誤差較小;未來6 h波高預測結果中,M0數據模型預測結果誤差較大,M1、M2數據模型預測效果較好;未來9 h及12 h波高預測結果中,M0和M1數據模型預測結果與真實波高的趨勢基本一致,但誤差均較大,M2數據模型對于短時間的波高預測,其雖輸入的特征過多,增加了計算時間,但對未來12 h波高有一定預測能力,仍能較好反映出有效波高受環境影響的變化結果。
4 結 論
基于GWO-SVR方法,建立了3種預測數據模型展開有效波高預測試驗,結果表明,GWO-SVR能顯著提高有效波高預測精度;GWO-SVR算法和PSO-SVR算法有效波高預測結果表明,GWO-SVR算法預測結果的平均誤差低于PSO-SVR算法,且不易陷入局部最優;使用較大空間范圍的海洋環境數據構建特征訓練GWO-SVR算法并進行預測,可有效減少其預測誤差。

