基于MM-GGIW-PMBM 濾波的擴展目標跟蹤算法

吳孫勇, 周于松, 謝蕓, 蔡如華, 樊向婷

(1. 桂林電子科技大學 數學與計算科學學院, 桂林 541004; 2. 廣西精密導航技術與應用重點實驗室, 桂林 541004)

多目標跟蹤(multiple target tracking, MTT)的目的是從一系列有噪聲、帶有雜波的測量數據中檢測和跟蹤目標。 在大多數應用(如雷達)中,由于目標和傳感器之間的距離較遠或者傳感器分辨率過低,目標被看作是點目標,每個點目標在每個時間間隔內最多產生一個測量值。 然而,隨著傳感器的分辨率越來越高,目標將占據傳感器的多個分辨率單元,使得單個目標在每次掃描時會產生多個量測,從而點目標的模型假設就不再成立,此時則需要將目標模型建模為擴展目標。 區別于傳統意義上的點目標,擴展目標的演化是遞歸估計目標外形和運動狀態的過程,每個目標在每個時刻可能會產生多個量測,其詳細的概述在文獻[1]中給出。

在貝葉斯框架下,Mahler[2]將隨機有限集(random finite set, RFS)應用于MTT 問題之中,早期基于RFS 的MTT 算法通過逼近后驗多目標密度的一階矩來跟蹤目標,如概率假設密度(probability hypothesis density, PHD)濾波器[3-5]和勢概率假設密度(cardinality PHD,CPHD)[6-7]濾波器。 而近年來基于RFS 的共軛MTT 問題引起了廣泛的關注,MTT[8]中的共軛性意味著所有的先驗和后驗概率密度都具有相同的函數形式,即通過共軛先驗可以為目標概率密度提供閉式解,理論上保證了最優。

在文獻中可以找到2 種類型的多目標濾波滿足共軛先驗的性質:廣義標簽多伯努利濾波(generalized labeled multi-Bernoulli filtering, GLMB)[8-9]和泊松多伯努利混合濾波(Poisson multi-Bernoulli mixture filtering, PMBM)[10]。 相較于GLMB,PMBM的濾波精度更高且計算代價更小。 PMBM 濾波允許將擴展目標集合劃分成2 個不相交的子集:已檢測到的目標集合和還沒有被檢測到的目標集合。 文獻[10]提出了一種GGIW-PMBM 濾波算法,該算法假設目標狀態服從伽馬高斯逆威夏特(Gamma Gaussian inverse Wishart,GGIW)分布[11],通過單一的運動模型對擴展目標的演化進行建模,然而當該運動模型無法與目標運動相匹配時,就會導致跟蹤精度下降。

在Granstr?m 等[10]提出的GGIM-PMBM 多機動擴展目標跟蹤算法中,本文結合交互式多模型[12-14](interacting multiple model, IMM)算法的思想,提出了一種多模型的GGIM-PMBM (MMGGIW-PMBM) 算法。 首先,在預測階段利用IMM算法融合多種運動模型,實現對擴展目標的混合估計;然后,引入強跟蹤濾波器(strong tracking filter, STF)的漸消因子,使輸出殘差正交,增強算法對目標的跟蹤能力和估計精度,使得當擴展目標在做機動運動時,能夠快速地為目標匹配準確的運動模型;最后,在PMBM 更新階段利用似然函數完成模型概率的更新。 此外,本文采用廣義最優子模式[15](generalized optimal sub-pattern assignment, GOSPA)距離衡量算法的跟蹤性能,該方法將誤差分解成目標位置誤差、漏檢目標數量和誤檢目標數量3 部分,能夠直觀地展現擴展目標跟蹤算法的性能。

1 模型框架

假設在k時刻將擴展目標建模為

式中:Nx,k為k時刻目標的數量;為第i個目標的泊松分布量測比率;為第i個目標質心的運動學狀態,包含目標的位置、速度及轉彎率等參數;為第i個目標的外形狀態,包含目標的形狀和大小。 將擴展目標建模為RFS,根據RFS 的性質,目標的勢(Nx,k)為時變離散隨機變量,目標的狀態()為隨機變量。

利用線性高斯動態模型[16]為多運動模型下目標的質心建模,即

式 中:M為 轉 移 模 型 總 數 量;為 第r個 模 型的轉移概率;為第r個轉移模型對應的過程噪聲,其均值為0,協方差為;為第r個模型對應的轉移矩陣;Id為單位矩陣,d為目標外形的維度;“?”表示克羅內克積。

假設Zk=為k時刻的量測集,其同樣被假設為RFS,通過線性高斯模型建模,可表示為

量測集合Zk由雜波量測和目標產生量測的并集組成,表示為

式中:θ(z)為由目標產生的量測;k(z)為雜波量測,假設它們相互獨立。 雜波量測k(z) =λc(z),λ為雜波量測數量對應的泊松率,c(z)為雜波的空間概率分布函數。

設擴展目標的狀態ξ的檢測概率為pD(ξ),如果被檢測到,產生的量測數量服從泊松分布,密度為γφ(),γ為目標產生的量測數量對應的泊松率,φ(z|ξ)為依賴目標狀態的量測分布函數。 則對于非空量測集(＞0),其似然函數可表示為

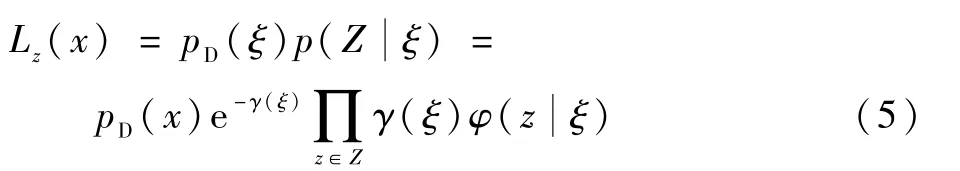
式中:p(ξ)為預測似然函數。 因為量測服從泊松分布,所以目標至少產生一個量測的概率為1 - e-γ(ξ),則 擴 展 目 標ξ的 有 效 檢 測 概 率 為pD(ξ)(1- e-γ(ξ)), 漏檢的概率可以表示為

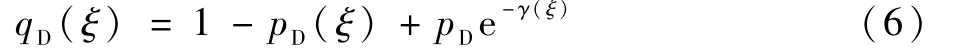
注意,qD(ξ)同樣也是量測集合為空集時的條件似然,即Lz=?(ξ) =qD(ξ),?為空集。

2 擴展目標狀態的概率密度分布

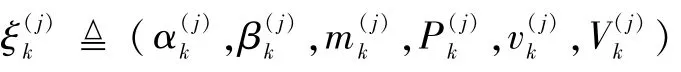
式中:Γ(·)為伽馬函數。

x～N(x;m,P)表示質心的運動學狀態分布,m為均值,P為協方差。

式中:etr(·) =exp(tr(·))表示矩陣跡的指數;Γd為多元伽馬函數。

根據式(7) ～式(9),擴展目標狀態數服從GGIW 分布,表示為

式中:ξ?(γ,x,X) 為擴展目標待估計狀態,ξ?(α,β,m,P,v,V)為GGIW 的分量參數。

3 泊松多伯努利混合濾波

3.1 泊松點過程

泊松點過程(Poisson point process, PPP)假設RFS 中目標數量服從泊松分布,且目標狀態之間獨立同分布。 PPP 可通過單目標狀態空間中的強度函數D(x)參數化,而強度函數D(x)可由未知目標數量對應的泊松率μ與擴展目標的分布函數f(x)的乘積表示,即D(x) =μf(x)。 此外,強度函數還具有一個重要的性質,即空間S中擴展目標的總數量可以由∫x∈SD(x)dx表示。 通過強度函數D(x),PPP 的密度可表示為

3.2 多伯努利混合過程

伯努利集合XB同樣為RFS,且集合XB中包含的變量最多只能有一個,其概率密度函數為

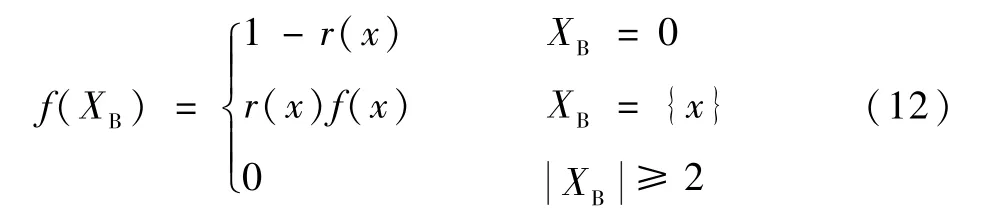
式中:r(x)為存活概率;f(x)為概率密度函數。在MTT,伯努利RFS 包含了單個目標存在情況的不確定性(通過r(x))和目標狀態x的不確定性(通過f(x))。

多伯努利(multi Bernoulli, MB)RFSXMB是固定數量的伯努利RFS(n∈Π,Π為索引集)的并集,可表示為

集合XMB概率密度函數為

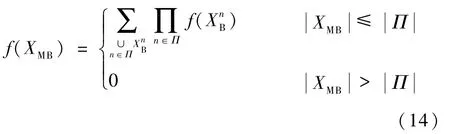
MB 的分布可通過其伯努利參數{r(x),f(x)}Π表示。

多伯努利混合(MB mixture, MBM)密度可以由一系列正則化且帶有權重的MB 的概率密度函數混合表示,即MBM 可以由{(ωs,{rs,n(x),fs,n(x)}n∈Πs)}s∈J定義,其中,J為MBM 中MB 的索引集合,Πs為第s個MB 中伯努利成分的索引集合,ωs為第s個MB 的權重。

3.3 PMBM 結構

PMBM 可以用2 個部分表示:一部分為PPP,用來估計多目標演化過程中存在但是并未被檢測到的目標,由符號Xu表示;另外一部分為MBM,用來估計多目標演化過程中已經被檢測到的目標的分布情況,由符號Xs表示。 因此,目標集合X可以劃分成2 個不相交的子集:

PMBM 密度函數可表示為

式中:fs,n(·)為第s個MB 中第n個伯努利的密度函數;設rs,n(·)為第s個MB 中第n個伯努利的存活概率,每個伯努利成分由GGIW 成分混合表示;為MBM 中MB 的數量;Πs為第s個MB 分量中伯努利的數量;Du為未知目標的強度函數。

則PMBM 可以通過參數表示為:Du,{(ωs,{rs,n(x),fs,n(x)}n∈Πs)}s∈J。

3.4 PMBM 濾波的遞歸算法

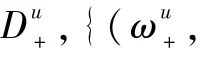
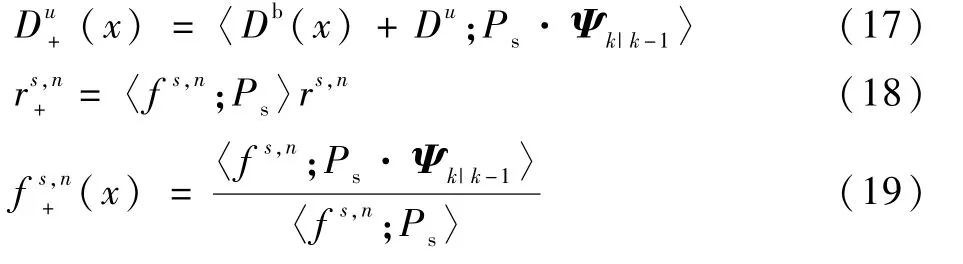
式中:Db(x)為新生分量強度函數;Ps為目標存活概率;Ψk|k-1為轉移矩陣的混合估計;=ωs。

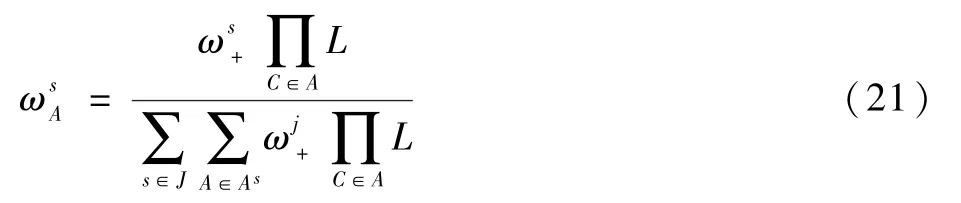
其中:L表示似然函數;A為伯努利成分的數據關聯;As為第s個MB 的數據關聯集合。

PPP 的密度Du為

4 MM-GGIW-PMBM 的遞歸

多模型PMBM 算法與單模型PMBM 算法的區別主要在預測階段。 因為擴展目標的概率密度函數可由式(10)表示,所以可以通過對參數α、β、m、P、v、V的預測來對GGIW 變量進行預測。 而多模型PMBM 算法在預測階段需要對參數α、β、m、P、v、V進行混合估計預測,且還要使用STF 修正預測之后的GGIW 的協方差,MM-GGIW-PMBM預測階段算法如下:

4.1 多模型GGIW 分量預測階段的混合估計

式中:M為運動模型的總數量;ηk-1,r為第r個模型下指數漸消因子;為k- 1 時 刻 第j個GGIW 分量對應第r個模型的概率;πir為模型i到模型r轉移概率;τk-1,r為擴展目標在第r個模型下的擴展靈敏度;T為采樣時間間隔;為第r個模型 對應 的 轉 移 矩 陣;為 第r個 模 型 對應的過程噪聲協方差。

4.2 強跟蹤濾波器修正

由于擴展目標跟蹤算法對轉移矩陣模型有非常嚴格的要求,當實際轉移模型參數發生變化時,會使濾波器的狀態估計出現較大偏差。 因此,通過引入一種STF,利用時變的漸消因子在線實時調整增益矩陣,從而自適應修正協方差,增強算法對機動目標的跟蹤能力。 第j個GGIW 分量的預測協方差的修正公式如下:

式中:Rk為量測噪聲協方差;Hk為量測矩陣;為第j個擴展目標的外形參數預測;λ0為弱化因子;為量測子集的數量。

4.3 GGIW 分量的更新

多模型PMBM 算法與單模型PMBM 算法在更新階段的區別在于多模型PMBM 算法需要對模型概率進行更新,MM-GGIW-PMBM 更新階段算法如下:

同時在更新階段完成模型概率的更新。 假設模型的總數量為M,則對于新生目標分量的模型概率為

未檢測到的目標分量和已檢測到的目標分量的模型概率更新方式相同,其模型概率為

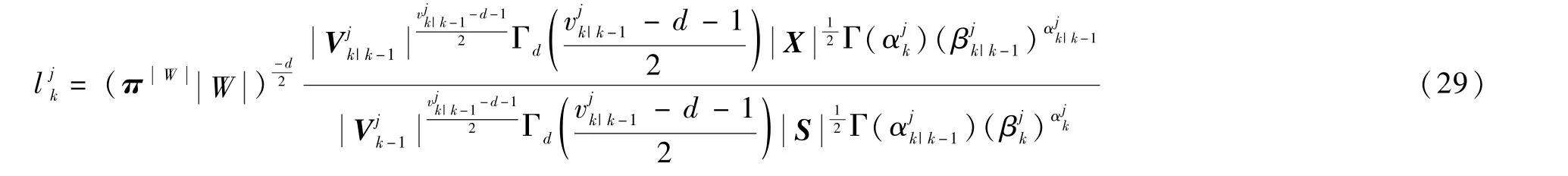
5 仿真實驗

5.1 性能評估

對于橢圓外形擴展目標估計的性能評價主要有6 種[17],其中,基于高斯Wassterstein 距離(Gaussian Wassterstein distance, GWD)[18]通常是最佳的選擇,而本文則是選擇文獻[15]中GOSPA多目標度量對所提算法進行評估,其定義為

5.2 仿真場景

在算法實驗場景中,假設目標的運動方式有2 種,分別為勻速直線(CV)轉彎(CT)運動,對應的模型轉移矩陣為

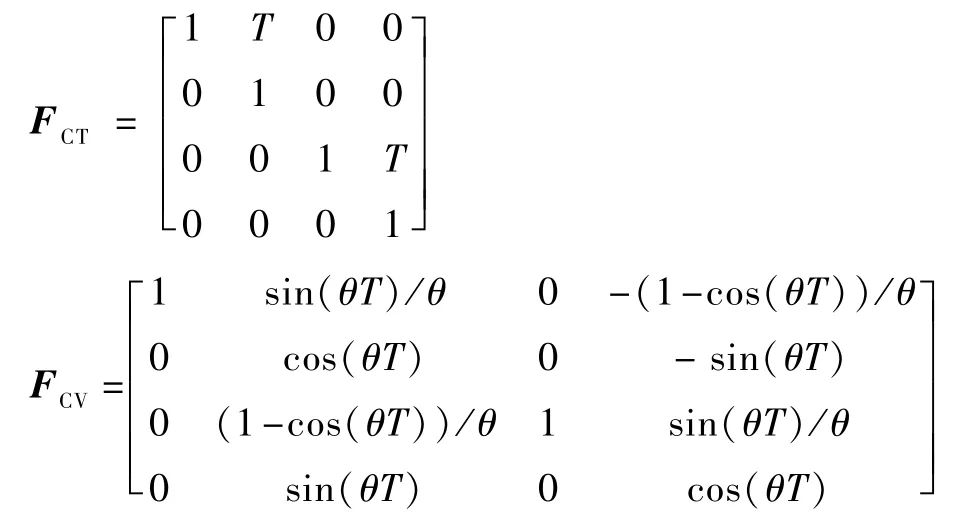
其對應的過程噪聲分別為

式中:T=1 s 為時間采樣間隔長度。 STF 的弱化因子λ0=1,擴展目標的檢測概率Pd =0.8,存活概率Ps =0.99,雜波服從均值為60 的泊松分布,模型i到模型r轉移概率矩陣為

5.3 算法性能對比

在圖1 和圖2 中,存在3 個擴展目標在設定的雜波環境中運動。 第1 個目標質心的初始運動信息為[ - 75 m; - 2 m/s; - 75 m;2 m/s],在1 ～5 s做勻速直線運動,在6 ～20 s 做角速度為-0.2 rad/s的轉彎運動,在21 ～30 s 做角速度為0.3 rad/s 的轉彎運動。 第2 個擴展目標質心的初始運動信息為[ -75 m; -2 m/s;75 m;2 m/s],在10 ～14 s 做勻速直線運動,在15 ～20 s 做角速度為-0.2 rad/s 的轉彎運動,在21 ～30 s 做角速度為0.3 rad/s 的轉彎運動。 第3 個擴展目標質心的初始運動信息為[75 m;2 m/s;75 m;2 m/s],在7 ～11 s 做勻速直線運動,在12 ～20 s做角速度為-0.2 rad/s 的轉彎運動,在21 ～30 s做角速度為0.3 rad/s 的轉彎運動。 3 個擴展目標的橢圓外形的長短軸相同,分別為0. 8 m 和1 m,初始概率分別為[1/3,1/3,1/3],各運動模型對應伽馬分布指數的漸消因子分別為2、2、3,而外形隨時間變化的靈敏度分別為τ=9、10、10,圖1 采用的是MM-GGIW-PMBM 算法,圖2 采用的是GGIW-PMBM 算法。 可以看出,相較于采用單個運動模型的GGIW-PMBM 算法,MM-GGIWPMBM 算法對擴展目標的估計更加精確穩定。

圖1 MM-GGIW-PMBM 算法下擴展目標運動軌跡及其估計軌跡Fig.1 Trajectory of extended target and its estimated trajectory by MM-GGIW-PMBM algorithm

圖2 GGIW-PMBM 算法下擴展目標運動軌跡及其估計軌跡Fig.2 Trajectory of extended target and its estimated trajectory by GGIW-PMBM algorithm

為了進一步驗證本文算法的精度及有效性,將MM-GGIW-PMBM 算法與相同條件下的MMGGIW-PHD 算法做對比,一共進行100 次蒙特卡羅實驗取估計誤差均值,且每一次實驗目標運行100 個時刻,共對27 個目標進行跟蹤,目標出生及消失的時刻各不相同,在第58 個時刻之前跟蹤的目標數量較少,第58 個時刻之后目標數量較多。

圖3 和圖4 分別為目標數量的估計及目標數量誤差的估計。 可以看出,在第58 個時刻之前,由于目標數量較少,MM-GGIW-PMBM 算法估計精度只是略高于MM-GGIW-PHD 算法,但在第58個時刻之后,目標數量增多,MM-GGIW-PHD 算法估計誤差出現大幅度波動,而MM-GGIW-PMBM算法估計誤差則保持穩定,這是因為PHD 濾波通過泊松分布近似目標的數量分布,但是由于泊松分布的均值與協方差相等這一特性,即目標數量過多時,其估計的誤差也會隨之增大。

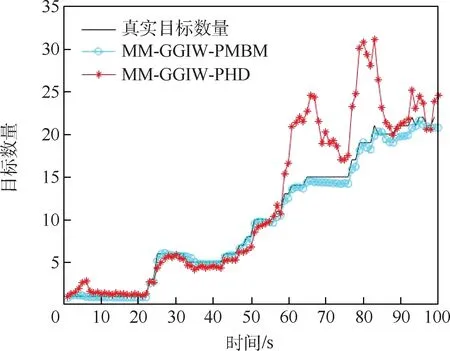
圖3 兩種算法對目標數量的估計對比Fig.3 Comparison of two algorithms for estimating target numbers

圖4 兩種算法對目標數量的估計誤差對比Fig.4 Comparison of two algorithms for estimating error of target numbers

由于GOSPA 算法的特殊性,可以將GOSPA誤差分為目標位置誤差、漏檢目標數量及誤檢目標數量3 部分。 其中,2 種算法GOSPA 距離估計的誤差如圖5 所示,即擴展目標位置誤差、漏檢目標數量及誤檢目標數量總體誤差對比;圖6 為2種算法對目標位置估計的誤差;圖7 為2 種算法對漏檢目標數量的估計;圖8 為2 種算法對誤檢目標數量的估計。 從圖5、圖7 和圖8 中可以看出,當目標數量較少時,相較于MM-GGIW-PHD算法,雖然MM-GGIW-PMBM 算法對擴展目標的GOSPA 距離誤差、漏檢目標數量及誤檢目標數量估計更加精確穩定,但這種優勢并不明顯,甚至對目標位置的估計(在圖6 給出)精度還要略低于MM-GGIW-PHD 算法。 而當目標的數量較多時,隨著量測信息的積累,MM-GGIW-PMBM 算法在GOSPA 距離誤差、漏檢目標數量及誤檢目標數量這3 方面的估計精度要遠強于MM-GGIW-PHD算法,其對目標位置的估計精度也強于MMGGIW-PHD 算法。

圖5 兩種算法GOSPA 距離估計誤差對比Fig.5 Comparison of GOSPA distance estimation errors between two algorithms

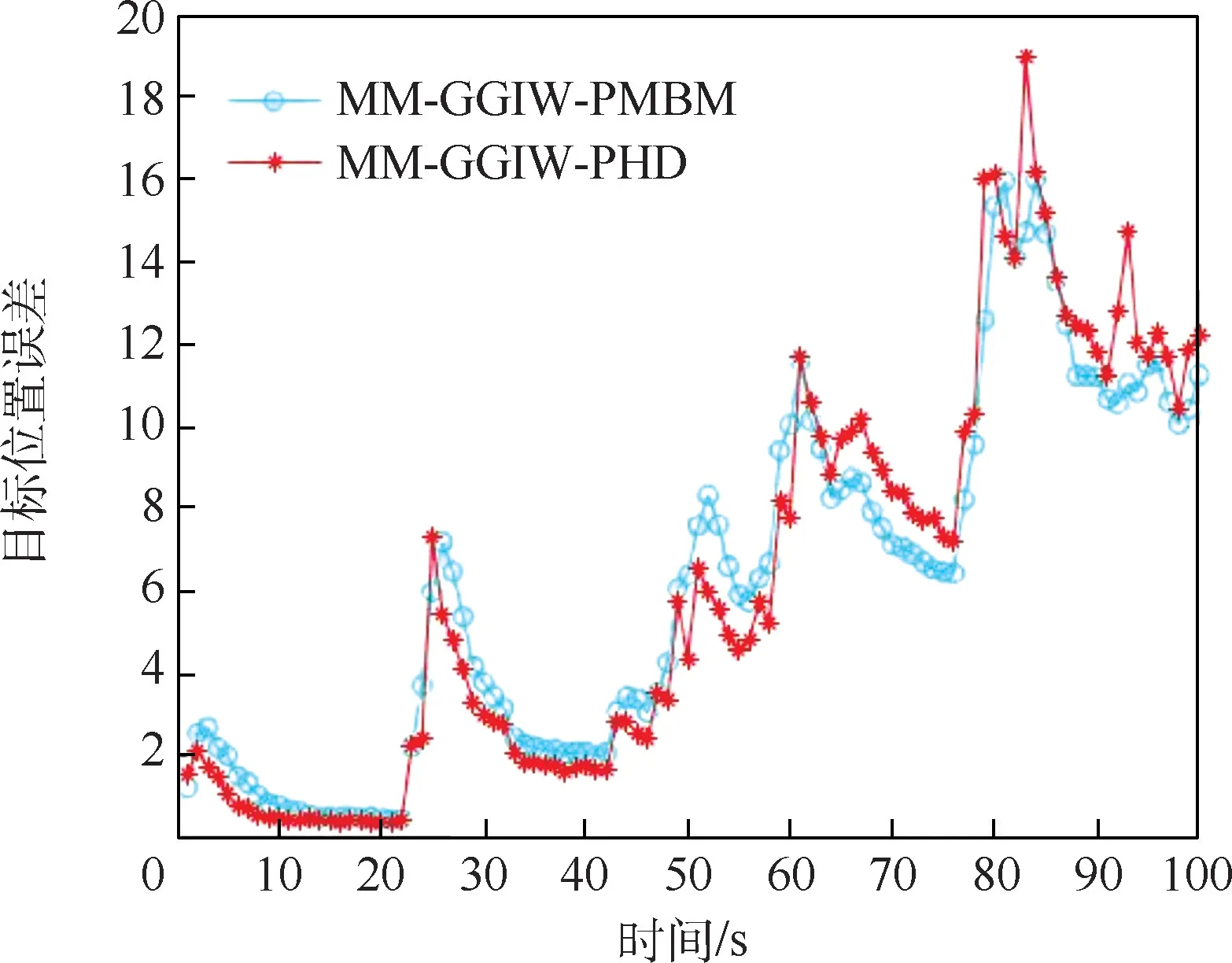
圖6 兩種算法目標位置估計誤差對比Fig.6 Comparison of target location estimation errors between two algorithms

圖7 兩種算法漏檢目標數量估計對比Fig.7 Comparison of estimating missed target numbers between two algorithms

圖8 兩種算法誤檢目標數量估計對比Fig.8 Comparison of estimating false detection target numbers between two algorithms

6 結 論

1) 針對擴展目標的機動問題,提出了一種MM-GGIW-PMBM 算法,利用隨機矩陣法將擴展外形建模成橢圓,再使用GGIW 分量描述擴展目標狀態。

2) 仿真結果表明在擴展目標的交互式算法中引入強濾波跟蹤的有效性,在相同條件下,當目標做機動運動時,傳統的單模型GGIW-PMBM 算法會逐漸跟丟目標,不能對多機動擴展目標進行有效的估計,而MM-GGIW-PMBM 算法在目標做機動運動時能夠快速做出調整。

3) 相較于MM-GGIW-PHD 算法,當目標數量較多時,MM-GGIW-PMBM 算法能夠更加穩定有效地對目標進行估計。