濕熱環(huán)境中含脫層復(fù)合材料層合板的界面裂紋擴(kuò)展

夏飛, 薛江紅, 何贊航, 金福松

(暨南大學(xué) 力學(xué)與建筑工程學(xué)院, 廣州 510632)

纖維增強(qiáng)復(fù)合材料是由高強(qiáng)度、高剛度的纖維作為增強(qiáng)材料,與基體材料進(jìn)行模壓、纏繞等方式形成宏觀上具有新性能的材料。 相對于傳統(tǒng)材料,纖維增強(qiáng)復(fù)合材料具有比強(qiáng)度高、耐腐蝕性好、可設(shè)計(jì)性好等優(yōu)點(diǎn),在機(jī)械化工、航空航天等眾多領(lǐng)域得到廣泛應(yīng)用。 對于復(fù)合材料層合結(jié)構(gòu),在加工使用過程中極易出現(xiàn)損傷,層間脫層是復(fù)合材料層合板殼結(jié)構(gòu)的一種常見缺陷或損傷形式,主要發(fā)生在層板的界面上。 層合板殼結(jié)構(gòu)發(fā)生脫層擴(kuò)展的根本原因是脫層前沿處的應(yīng)力累積,由于前沿處應(yīng)力場分布的奇異性,作為層間斷裂韌性表征量的臨界應(yīng)變能量釋放率得到廣泛應(yīng)用[1]。 同時(shí),環(huán)境中溫度和濕度的改變也會在復(fù)合材料層合板內(nèi)部產(chǎn)生濕熱應(yīng)力,削弱層合板的承載能力。 因此,分析濕熱環(huán)境中復(fù)合材料層合板結(jié)構(gòu)在壓縮荷載下的非線性后屈曲、脫層擴(kuò)展等力學(xué)行為,是一項(xiàng)極具工程意義的工作。

關(guān)于含脫層復(fù)合材料層合板殼的非線性力學(xué)研究,Chai 等[2]最先提出一維穿透脫層分析模型,研究脫層層合板的整體失穩(wěn)。 劉述倫等[3]討論了含有貫穿脫層復(fù)合材料層合板的力學(xué)性能與濕度和溫度之間的關(guān)系,并給出了屈曲問題的解答。 周宇等[4]考慮含纖維搭橋的影響,建立了用撓度和應(yīng)力函數(shù)表示的正交各向異性材料矩形脫層屈曲非線性方程組。 李萍等[5]考慮接觸效應(yīng),研究了單向鋪設(shè)的層合梁的非線性后屈曲路徑。K?llner 和V?llmecke[6-7]提出了一種分析模型,該模型僅用廣義坐標(biāo)就可模擬層合板的后屈曲行為和分層損傷。 文獻(xiàn)[2-7]都是基于經(jīng)典板殼理論,忽略板在橫向界面處由于剪力引起的橫向剪切變形,由于層合板/殼對橫向剪切變形很敏感[8],由此發(fā)展出適用于中厚板的剪切變形理論。 基于一階剪切變形理論(first order shear deformation theory, FSDT)及分層理論,Nikrad 等[9]研究了含集合缺陷的復(fù)合材料層合板的后屈曲行為,并與有限元結(jié)果進(jìn)行了對比驗(yàn)證。 同樣考慮FSDT,Wang等[10]研究了含橢圓分層的復(fù)合材料層合板的壓縮破壞,所建立的模型與實(shí)驗(yàn)結(jié)果一致。 Shabanijafroudi 和Ganesan[11]則給出了一種新的脫層模型數(shù)學(xué)建模方法,與有限元的算例驗(yàn)證中證明該方法可以降低求解的計(jì)算量。

復(fù)合材料層合板的脫層擴(kuò)展一般分為:Ⅰ型張開、Ⅱ型滑移和Ⅲ型撕裂。 Pereira 和Morais[12]建立梁模型計(jì)算能量釋放率,并結(jié)合實(shí)驗(yàn)和虛擬裂紋閉合技術(shù),分析了復(fù)合材料層合結(jié)構(gòu)的Ⅰ+Ⅱ混合型層間斷裂。 鄭偉玲和鄭龍席[13]發(fā)展了一種通過位移來計(jì)算3 點(diǎn)彎曲梁模型中裂紋能量釋放率的方法。 任雷和盛冬發(fā)[14]建立了二維有限元模型,分析了單向纖維增強(qiáng)復(fù)合材料板I 型裂紋的尖端應(yīng)力場。 Tay 等[15]綜合使用擴(kuò)展有限元(extended finite element method, XFEM)和內(nèi)聚力單元(cohesive element, CE),模擬了復(fù)合材料漸進(jìn)損傷過程3D 分層和基體開裂及兩者之間的相互作用。 鄧健等[16]基于經(jīng)典層合板理論及雙線性黏聚區(qū)本構(gòu)關(guān)系,提出一種I-II 混合型斷裂的裂紋擴(kuò)展理論模型。

文獻(xiàn)[12-16]關(guān)于界面裂紋的研究大多基于實(shí)驗(yàn)和有限元仿真,從模型受載和邊界的形式來看,研究主要集中于雙懸臂染(double cantilever beam, DCB)、端部切口彎曲(end notched flexture,ENF)、 混 合 模 式 彎 曲(mixed mode bending,MMB)層合試件,對于承受面內(nèi)荷載作用的含初始脫層層合板裂紋擴(kuò)展的理論研究還不多。 為了深入探討含脫層復(fù)合材料層合結(jié)構(gòu)的承載能力,Xue 等[17-19]開展了系列研究,詳細(xì)討論了接觸效應(yīng)與模態(tài)解的關(guān)系,并提出由于接觸的存在,含脫層層合板呈現(xiàn)的是整體一致的屈曲模態(tài)和后屈曲變形,在面內(nèi)壓縮荷載作用下,含脫層層合板發(fā)生Ⅱ型面內(nèi)滑移擴(kuò)展,研究表明,脫層界面發(fā)生擴(kuò)展的主要原因是層間剪應(yīng)力的累積,也與后屈曲階段橫向剪力和剪切變形的增加有關(guān)。 本文基于FSDT,分析了承受軸壓作用的復(fù)合材料層合板在脫層界面的裂紋擴(kuò)展行為。 建立含脫層復(fù)合材料層合板的四分區(qū)模型,考慮環(huán)境濕熱和脫層界面的接觸效應(yīng)的影響,推導(dǎo)脫層復(fù)合材料層合板在濕-熱-力載荷作用下的總勢能,并求解非線性后屈曲的控制方程。 結(jié)合斷裂力學(xué)中的斷裂準(zhǔn)則,給出脫層擴(kuò)展的能量釋放率表達(dá)式,并進(jìn)一步求得脫層界面發(fā)生擴(kuò)展時(shí)的臨界壓縮載荷。 通過開發(fā)MATLAB 程序代碼進(jìn)行數(shù)值計(jì)算,討論了脫層幾何尺寸和濕熱環(huán)境對復(fù)合材料層合板承載能力的影響。

1 基本理論

1.1 數(shù)學(xué)模型

考慮一含初始貫穿脫層的復(fù)合材料矩形中厚板,其長為a、寬為b、高為h,由厚度為h0的單層板以一定角度鋪設(shè)黏合而成。 邊界條件為四邊簡支,左右兩側(cè)受軸向壓縮荷載Nx的作用。 為便于分析,將脫層復(fù)合材料層合板模型簡化為可計(jì)算的四分區(qū)數(shù)學(xué)模型,如圖1 所示。 脫層長度為L2,與上表面的距離為h2,脫層左前沿與左邊界的距離為L1,由此將模型分為4 個層板,分別記為子層合板Ω(i),i=1,2,3,4。 隨著縱向壓縮載荷的增加,脫層前沿裂紋將擴(kuò)展δni,各子層合板的邊界及尺寸也隨之發(fā)生變化。

圖1 含脫層復(fù)合材料層合板的四分區(qū)模型Fig.1 Four region modeling of delaminated composite laminates

假設(shè)層合板在發(fā)生變形時(shí)y-z橫截面和x-z橫截面的轉(zhuǎn)動角度分別為和,則考慮FSDT的層合板的位移場u(i)、v(i)、w(i)為

式中:

在濕熱環(huán)境中,層合板的應(yīng)力場分布受到濕熱力和機(jī)械力的共同影響,用[N(i)]E(、、)E和[]E(、、)E分別表示層合板的總薄膜內(nèi)力和總彎矩,即

式中:[N(i)]和[M(i)]分別為機(jī)械內(nèi)力和內(nèi)力矩;[N(i)]T和[M(i)]T分別為熱內(nèi)力和熱力矩;[N(i)]H和[M(i)]H分別為濕內(nèi)力和濕力矩。

濕熱內(nèi)力和內(nèi)力矩為[20]

設(shè)[σ]為應(yīng)力分量,[ε]為應(yīng)變分量,則有

其中:θ為鋪設(shè)角;α1、α2為熱膨脹系數(shù),β1、β2為濕膨脹系數(shù),均由實(shí)驗(yàn)測得;單層板的折減剛度系數(shù)的各分量為

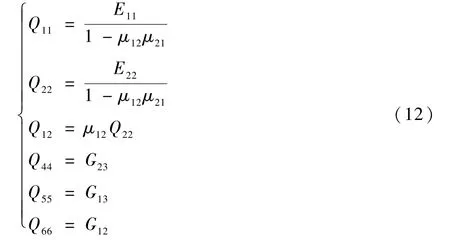
式中:E11、E22分別為材料在1、2 彈性主方向上的彈性模量;G12為材料在1-2 平面內(nèi)的剪切彈性模量;μ12和μ21為泊松比。

由式(2)和式(9),得到濕熱環(huán)境中正交對稱鋪設(shè)的層合板的本構(gòu)關(guān)系為

層合板在發(fā)生面外彎曲變形時(shí),脫層界面處的上子板Ω(2)和下子板Ω(3)之間受到一對相互作用的接觸力q*作用,導(dǎo)致上下子板Ω(2)和Ω(3)之間載荷的重新分配。 用線彈簧模型模擬層間接觸力與上下子板彎形w(2)和w(3)的關(guān)系[17]:

式中:接觸系數(shù)ke為

1.2 能量分析

靜力平衡狀態(tài)下,含脫層復(fù)合材料層合板所受的外力功為

式中:C(i)為子板Ω(i)的邊界;和分別為子板Ω(i)邊界上的廣義外力和廣義位移,可以表示為

在濕-熱-力載荷的共同作用下,含脫層復(fù)合材料層合板內(nèi)的彈性勢能為

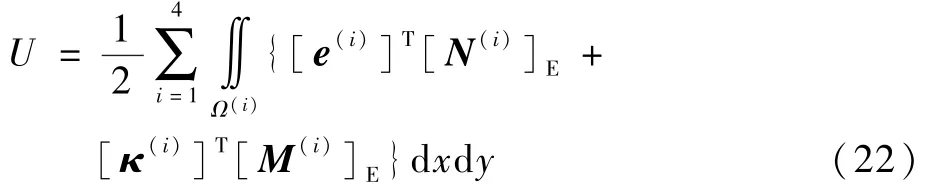
設(shè)脫層發(fā)生的虛擴(kuò)展為δni,系統(tǒng)內(nèi)總勢能改變量的變分形式δΠ為

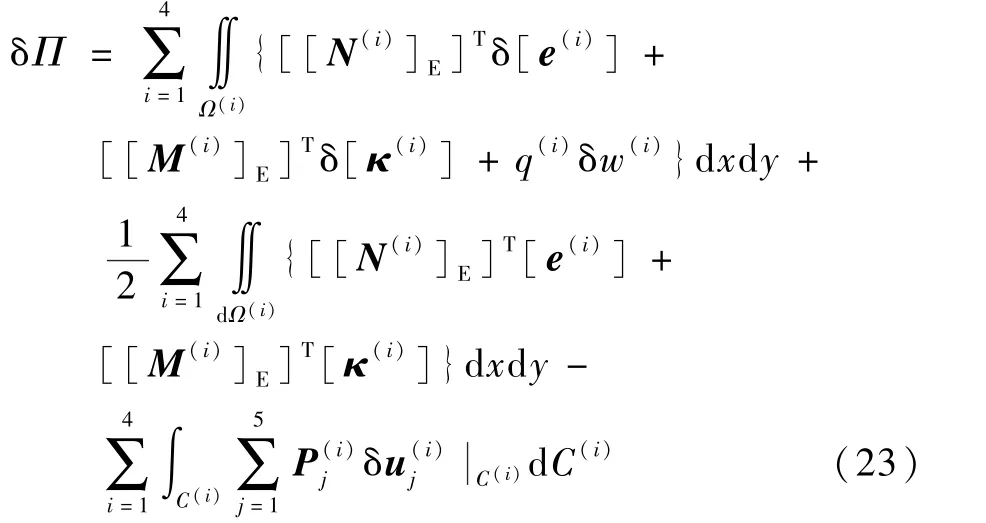
本文分析的是受軸向壓縮載荷作用的復(fù)合材料層合板,考慮到復(fù)合材料層合板較弱的層間屬性及初始脫層的存在,故假定裂紋的擴(kuò)展路徑是在脫層前沿處沿著層間方向發(fā)展。 根據(jù)可動邊界變分原理,在動邊界上的廣義位移(j= 1,2,…,5)的變分形式為

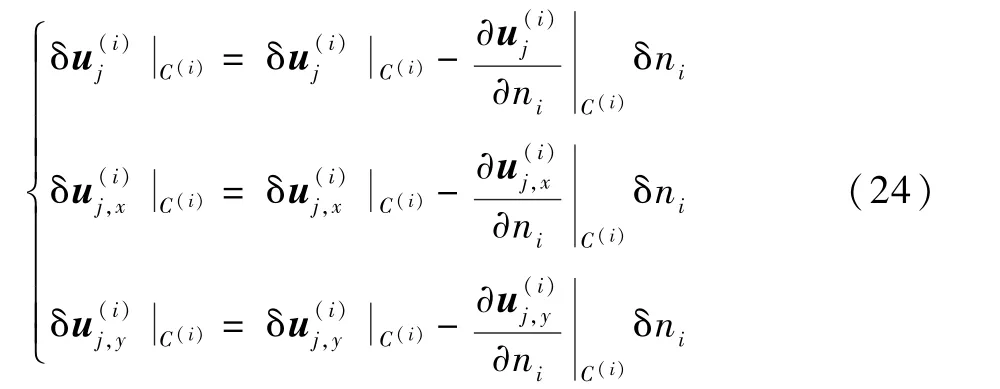
式中:δni為脫層擴(kuò)展的方向,用δn表示脫層前沿邊界發(fā)生正方向擴(kuò)展,則有

將式(24)和式(25)代入式(23)后,系統(tǒng)總勢能改變量的變分δΠ可拆分為2 部分:

式中:

式中:li和mi分別為子板Ω(i)的邊界法線在x軸和y軸上的方向余弦。 對于本文的模型,層間裂紋的擴(kuò)展方向只會沿著x軸,故mi應(yīng)取為0。 δΠ1是脫層邊界不變時(shí),脫層板系統(tǒng)的勢能改變量,根據(jù)虛功原理,系統(tǒng)保持靜態(tài)平衡的必要條件為

δΠ2為脫層板在動邊界上發(fā)生擴(kuò)展時(shí)的總能量變化量。 從圖1 中可以看出,由于模型的對稱性,層合板位移函數(shù)u、v和轉(zhuǎn)角函數(shù)φx是x坐標(biāo)的奇函數(shù),轉(zhuǎn)角函數(shù)φy是y坐標(biāo)的奇函數(shù),位移函數(shù)w是x、y坐標(biāo)的偶函數(shù);同時(shí)左右兩邊脫層前沿處的擴(kuò)展能量變化相同,故脫層板在發(fā)生擴(kuò)展時(shí)的總能量變化量δΠ可以簡化為

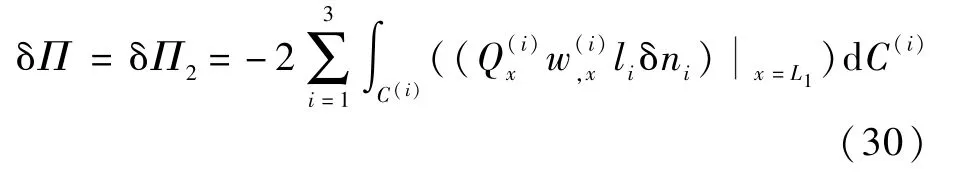
相對應(yīng)的,脫層板在發(fā)生擴(kuò)展時(shí)的總面積變化量為

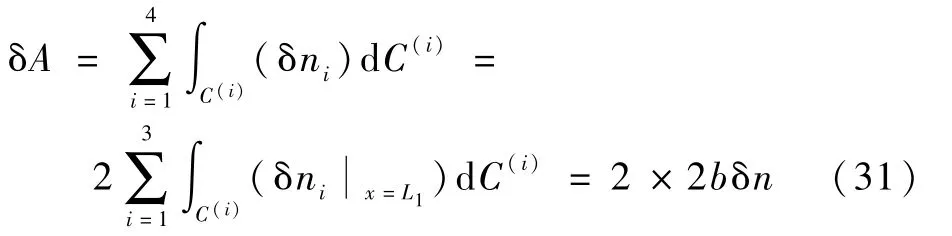
根據(jù)能量釋放率的定義,本文分析的受壓脫層板在脫層前沿處的能量釋放率為

1.3 靜態(tài)平衡方程及定解條件

對于承受壓縮荷載作用的含脫層層合板,式(27)和式(29)中給出了脫層板在靜態(tài)平衡下的基本控制方程和邊界連續(xù)性條件。 根據(jù)彈性力學(xué)知識,首先引入應(yīng)力函數(shù)Φ,有

將式(33)代入式(29),得到用位移函數(shù)w(i)和轉(zhuǎn)角函數(shù)和表示的脫層板的非線性控制方程組:

同時(shí),脫層板的邊界條件為四邊簡支。 結(jié)合板在脫層前沿處的連續(xù)性條件,求解上述靜態(tài)控制方程組的定解條件如下。

在y=0 處,

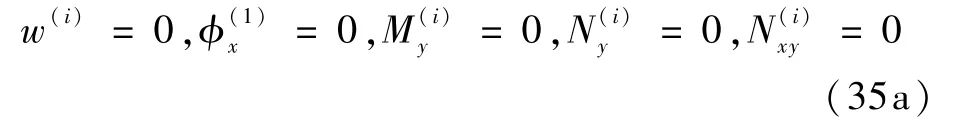
在y=b處,

在x=0 處,

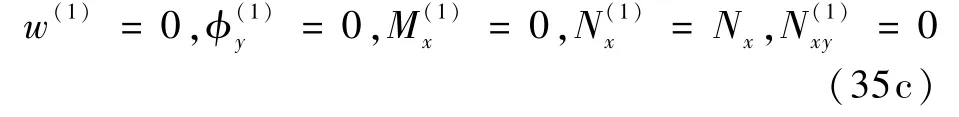
在x=a處,

在x=L1處(i=1)和x=L1+L2處(i=4),

2 攝動求解

求解非線性控制方程式(34)的精確解比較困難,本文提供一種數(shù)值解法——小參數(shù)攝動法進(jìn)行求解。 為方便攝動運(yùn)算,引入如下形式的無量綱參數(shù):

將式(37)代入式(34) ～式(36)中,得到無量綱形式的控制方程和定解條件。 選取ˉw0(ˉw0=

wmax/h)為攝動小參數(shù),對式(34)中所有變量進(jìn)行如下形式的攝動展開:

把攝動展開式(38)代入無量綱后的控制方程式(34)及定解條件式(35)和式(36)中,得到關(guān)于的多項(xiàng)式,根據(jù)的階次依次提取一階、二階和更高階的控制方程,并逐次進(jìn)行求解。 本文主要求解前兩階方程,對應(yīng)求得脫層板的屈曲解和后屈曲響應(yīng)。 將式(37)和式(38)代入式(34)中,按照ˉw0的階次合并同類項(xiàng),其中一階攝動方程為

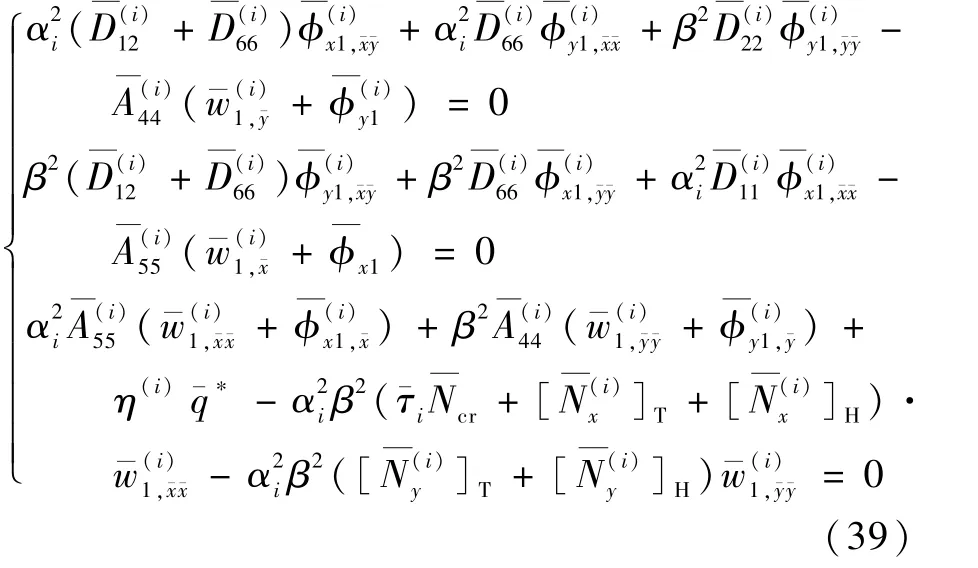
由于接觸力的存在,子板Ω(2)和子板Ω(3)的控制方程是耦合方程,需要一起求解。 將式(40)代入式(39),得到

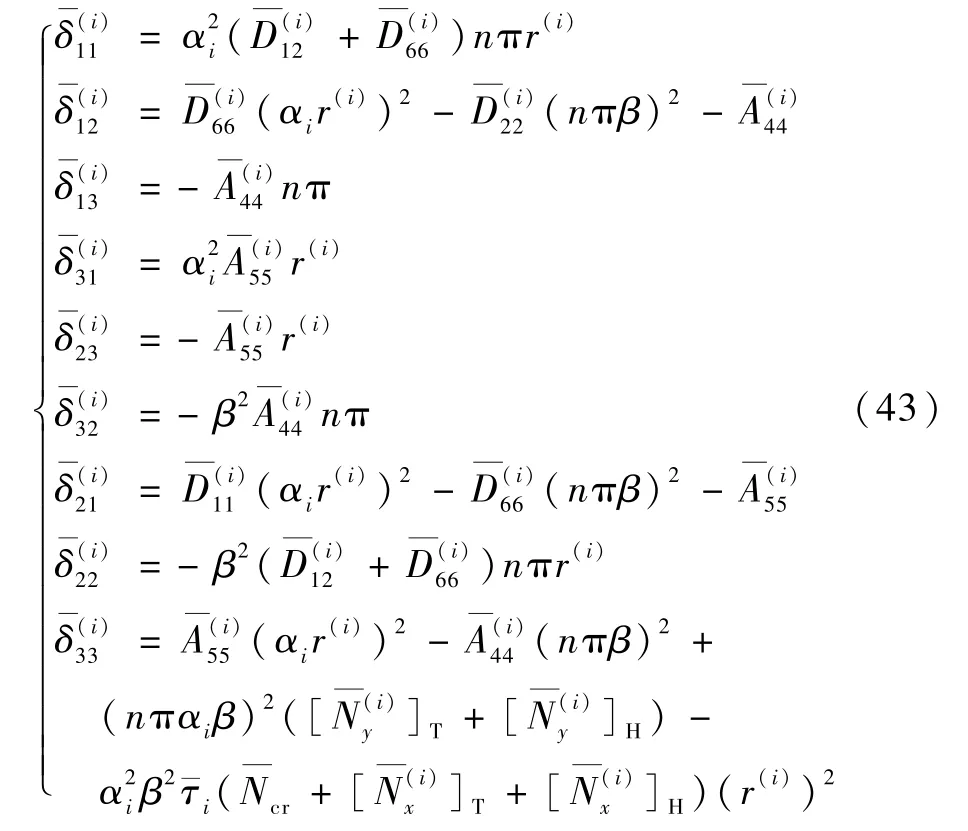
式(41)和式(42)成立的必要條件是其系數(shù)矩陣等于0,由此得到關(guān)于模態(tài)參數(shù)r(i)的特征方程:

用復(fù)數(shù)根的形式表示模態(tài)參數(shù)r(i)為

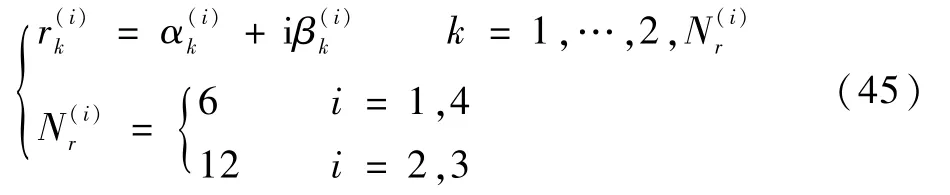
將式(46)代入式(39)的前兩式,即可確定其值:

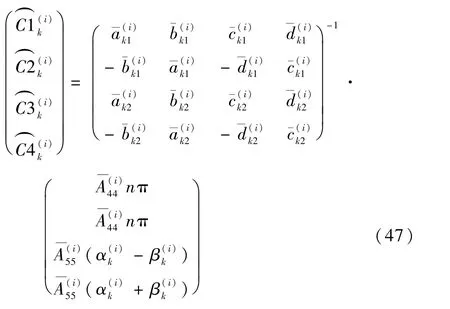
式中:

將式(46)代入無量綱后的定解條件式(35)和式(36)中,建立下面的齊次方程組:

式中: [R()] 為一個24 ×24 的系數(shù)矩陣。

式(49)成立的必要條件是系數(shù)矩陣等于0,即

(2)(1/2,1/2) =1,即可求得24 個待定系數(shù)[…,從而確定式(46)。 二階攝動方程為

假設(shè)二階攝動方程的形式解為

將式(46)代入式(51),并根據(jù)方程左右一一對應(yīng)關(guān)系可確定式(53),其中,為相關(guān)系數(shù)。通解需要用Galerkin 方程進(jìn)行求解:

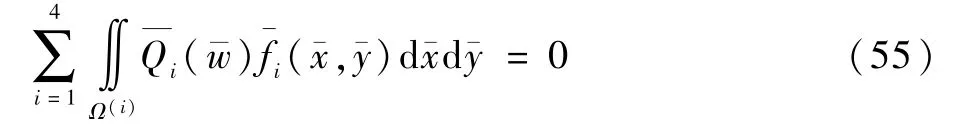
式中:

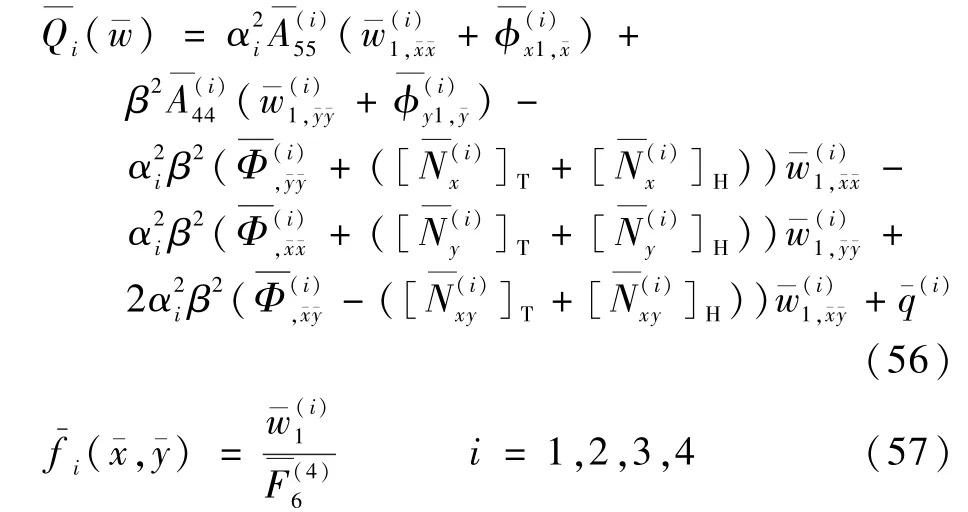
將式(56)和式(57)代入式(55)并進(jìn)行簡化得到后屈曲增量:

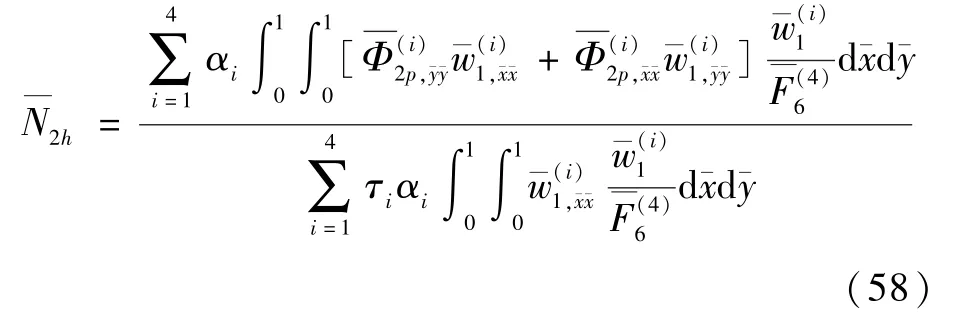
根據(jù)式(38)和式(58),可以確定脫層板在靜態(tài)壓縮時(shí)的后屈曲路徑為

將式(38)中位移函數(shù)和轉(zhuǎn)角函數(shù)的一階攝動展開式代入式(32),得到用一階攝動方程的解和表示的脫層板的能量釋放率:

根據(jù)斷裂力學(xué)的準(zhǔn)則,如果裂紋前沿處的能力釋放滿足G≥Gcr,則判定裂紋發(fā)生擴(kuò)展,其中Gcr為材料的斷裂韌性。 結(jié)合式(60),可以推導(dǎo)出脫層板發(fā)生脫層擴(kuò)展時(shí)的無量綱臨界擴(kuò)展載荷為

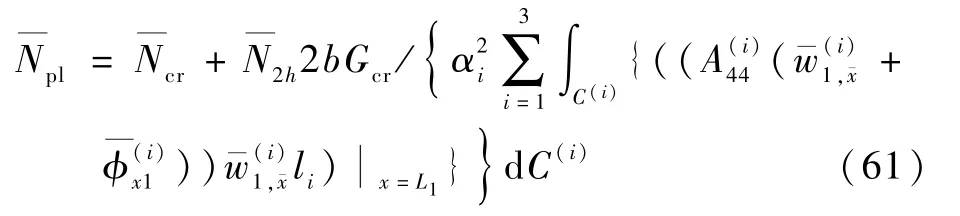
從式(32)和式(61)中可以看出,在幾何尺寸和材料參數(shù)確定的情況下,脫層界面發(fā)生裂紋擴(kuò)展時(shí)的能量改變δΠ主要由脫層前沿處的剪力項(xiàng)與橫向撓度有關(guān)項(xiàng)決定,承受軸向壓縮荷載的脫層板的Ⅱ型擴(kuò)展主要發(fā)生于板的后屈曲階段。 求解過程如圖2 所示。

圖2 求解流程Fig.2 Flow chart of solving process

3 算例分析

本文的研究對象主要為四邊簡支的含脫層復(fù)合材料層合板,本節(jié)對第2 節(jié)的理論推導(dǎo)進(jìn)行了驗(yàn)證和討論。 其中,算例分析中選用的材料參數(shù)[15]:E11=147 GPa,E22=10.3 GPa,G12=G13=7.0 GPa,G23=3.7 GPa,μ12=0.3,GIIC=547 N/m,α1= -0.3 ×10-6/℃,α2=28. 1 ×10-6/℃,β1=0,β2= 0. 44。 層合板的幾何參數(shù):a= 2 m,b=2 m,層合板的鋪設(shè)情況,按0°、90°、0°鋪設(shè),總共60 層[0°/90°/0°]20,h0=0.002 m。

3.1 有限元分析

為了驗(yàn)證理論解的正確性,開發(fā)ABAQUS 有限元軟件對含脫層復(fù)合材料層合板的屈曲行為進(jìn)行了數(shù)值模擬。 同樣采用四分區(qū)模型,在軟件中使用三維空間內(nèi)的可變形殼單元創(chuàng)建4 個層合板部件,保證板模型可以發(fā)生面外變形;然后通過裝配組合及在脫層前沿連接位置設(shè)置綁定約束,使得有限元模型與理論模型一致。 在脫層上下2 個部件的接觸面之間設(shè)置法向的硬接觸,以防止其發(fā)生互相貫穿。 在模擬溫度變化ΔT對層合板屈曲載荷的影響時(shí),首先在靜態(tài)通用分析步中計(jì)算溫度改變引起的熱應(yīng)力分布,然后把得到的結(jié)果設(shè)置為線性攝動屈曲分析步中的初始狀態(tài),進(jìn)而得出對應(yīng)溫度下的屈曲載荷。 整個有限元模型被劃分為13 000 個S4R 單元以滿足計(jì)算的精度,網(wǎng)格劃分情況如圖3 所示。

圖3 有限元網(wǎng)格劃分Fig.3 Diagram of finite element mesh partition

圖4 為考慮熱膨脹(ΔT=25 ℃,h2/h=0.1,L2/a=0.3)時(shí)的脫層板屈曲模態(tài)。 其中圖4(a)中考慮了接觸,從圖4(a)中可以看出脫層板的屈曲模態(tài)是整體一致的變形模態(tài),接觸效應(yīng)不可忽略,否則就會出現(xiàn)圖4(b)中上下層板相互貫穿這樣不合理的現(xiàn)象。 表1 列出了相對脫層深度一定(h2/h=0.2),不同相對脫層長度L2/a和溫度變化ΔT情況下,有限元屈曲結(jié)果(FEM)與當(dāng)前理論(FSDT)的比較,有限元模擬的屈曲結(jié)果同樣進(jìn)行式(37)中的無量綱處理。 從表1 中可以看出,有限元結(jié)果和理論結(jié)果較為吻合,2 種方法的差值比(Diff.)在5%之內(nèi),驗(yàn)證了理論推導(dǎo)的正確性。

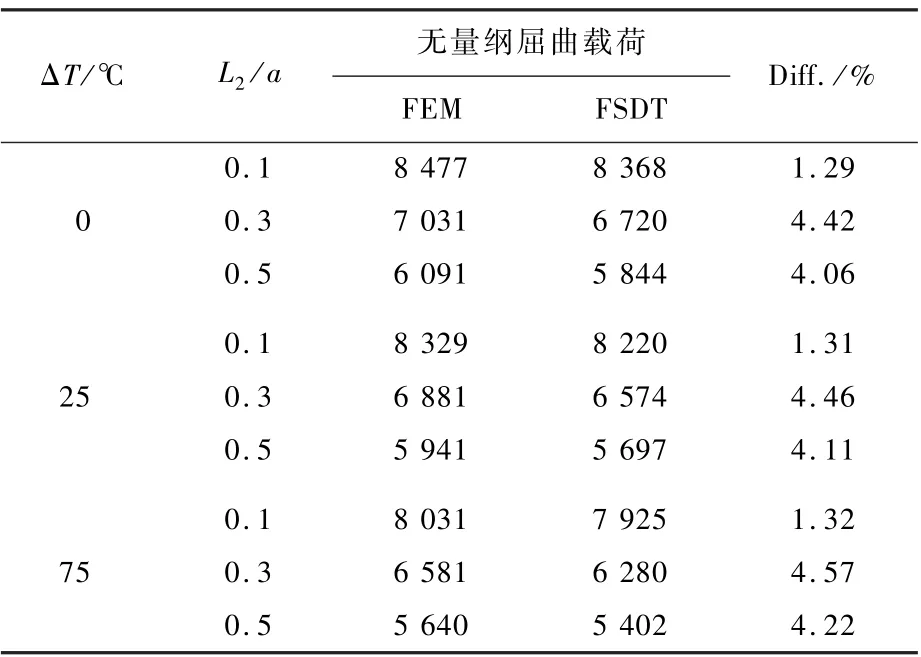
表1 含脫層復(fù)合材料層合板的有限元方法與理論方法的無量綱屈曲載荷比較Table 1 Compassion of non-dimensional buckling load between FEM and present method of delaminated composite laminates

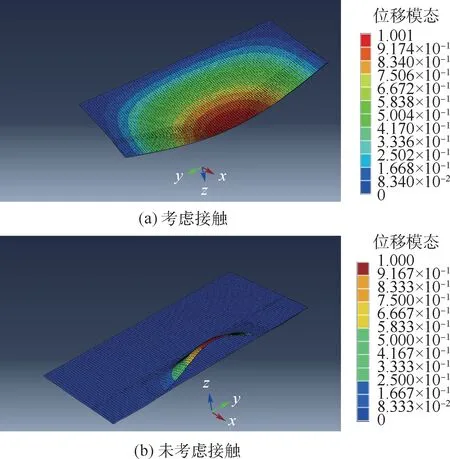
圖4 含脫層復(fù)合材料層合板屈曲模態(tài)Fig.4 Buckling mode of delaminated composite laminates

3.2 文獻(xiàn)對比

為了進(jìn)一步驗(yàn)證理論推導(dǎo)結(jié)果的有效性,將本文的結(jié)果與經(jīng)典層合板理論(CLPT)的解[18]進(jìn)行了比較。 表2 為在不同相對脫層深度h2/h和相對脫層長度L2/a情況下,在CLPT 和FSDT 下的無量綱屈曲荷載和無量綱臨界擴(kuò)展荷載的對比。 可以看出,盡管脫層深度和脫層長度不同,2 種方法得到的結(jié)果的差值比均不超過7%。同時(shí),CLPT 解總大于考慮FSDT 的解,這是由于CLPT 忽略橫向剪切變形,高估了層合板的剛度和承載能力。

表2 含脫層復(fù)合材料層合板的經(jīng)典層合板理論和剪切理論無量綱屈曲載荷和無量綱臨界擴(kuò)展載荷比較Table 2 Compassion of non-dimensional buckling load and non-dimensional threshold between CLPT and present method of delaminated composite laminates

3.3 脫層情況對臨界載荷的影響

圖5 為脫層深度(L2/a= 0. 3)和濕熱環(huán)境(ΔT=25 ℃, ΔC=0.1%)一定時(shí),脫層板的無量綱臨界荷載(屈曲載荷和臨界擴(kuò)展載荷)隨相對脫層深度(h2/h)的變化情況。 如圖5 所示,隨著脫層深度的增加,屈曲載荷呈現(xiàn)先減小后增大的趨勢,在脫層位于層合板中部h2/h=0. 5時(shí),屈曲載荷達(dá)到最小值。 臨界擴(kuò)展載荷也有同樣的變化趨勢,且總大于屈曲載荷。 在壓縮載荷作用下,脫層位置越靠近中間越容易發(fā)生脫層擴(kuò)展。

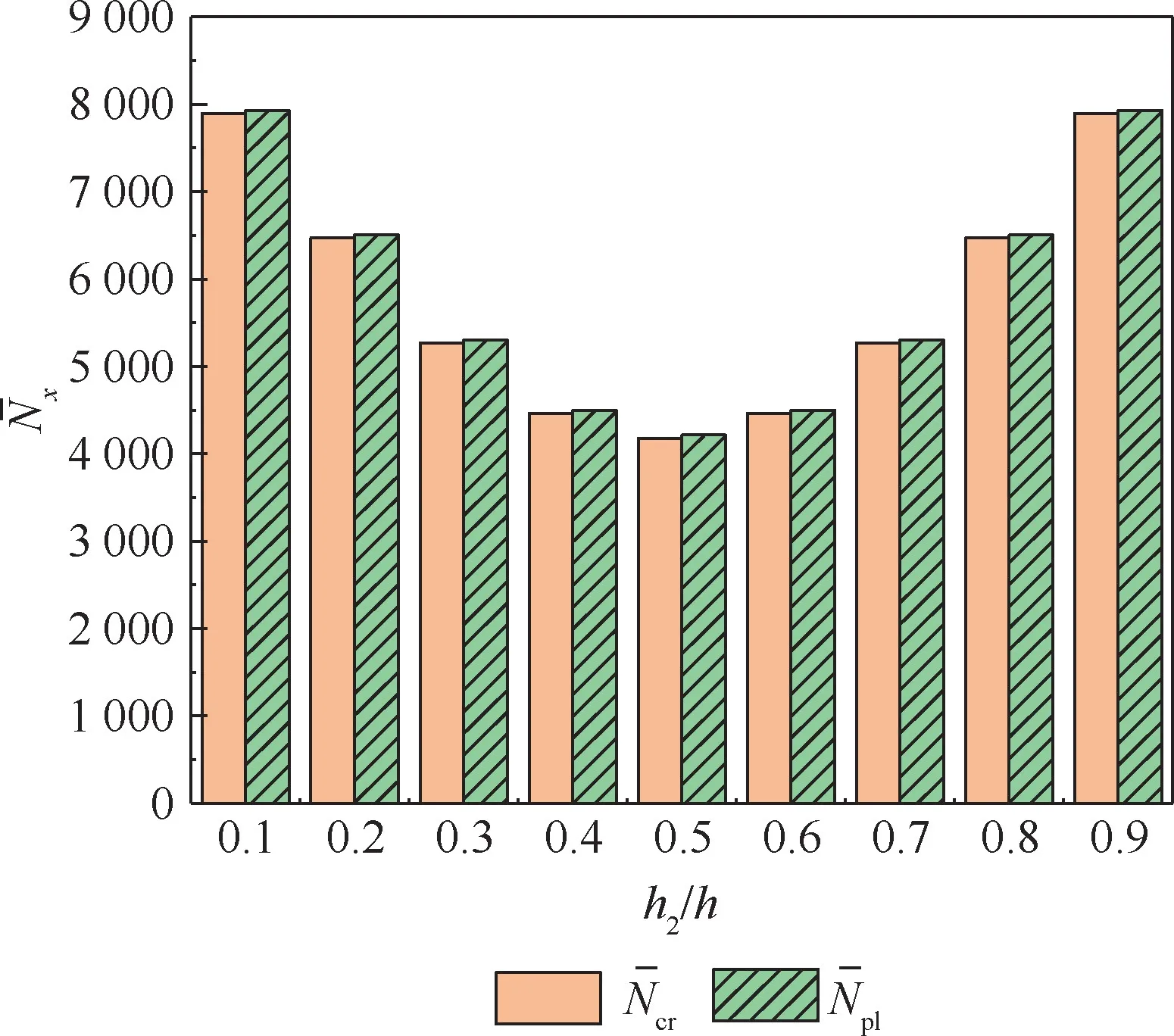
圖5 相對脫層深度對無量綱臨界載荷和的影響Fig.5 Effect of relative delamination depth on non-dimensional critical load and

圖6 為脫層深度(h2/h= 0. 3)和濕熱環(huán)境(ΔT=25 ℃, ΔC=0.1%)一定時(shí),脫層板的無量綱臨界荷載(臨界屈曲荷載和臨界擴(kuò)展荷載)隨相對脫層長度(L2/a)的變化情況。 由于數(shù)量級的關(guān)系,將相對脫層長度化分為3 個部分:圖6(a)為L2/a=0 ～0.02,圖6(b)為L2/a=0.02 ～0.2,圖6(c)為L2/a=0.2 ～1。 從圖6 中可以看出,屈曲載荷和臨界擴(kuò)展載荷均隨著相對脫層長度的增加而減小。 圖6(a)和圖6(b)顯示當(dāng)脫層長度趨近于0(無脫層)時(shí),擴(kuò)展載荷急劇增加且遠(yuǎn)遠(yuǎn)大于屈曲載荷;圖6(c)則相反,屈曲載荷和擴(kuò)展載荷同時(shí)變化且很接近,說明脫層長度越大,脫層越容易發(fā)生擴(kuò)展。 圖6 的曲線趨勢同時(shí)也表明脫層擴(kuò)展是一個持續(xù)的過程,當(dāng)靜態(tài)壓縮載荷達(dá)到或超過脫層板的擴(kuò)展載荷時(shí),就會導(dǎo)致脫層長度的增加,進(jìn)而導(dǎo)致脫層板的承載力下降,誘發(fā)脫層發(fā)生進(jìn)一步擴(kuò)展,直到層合板的完全破壞。

圖6 相對脫層長度對無量綱臨界載荷和的影響Fig.6 Effect of relative delamination length on non-dimensional critical load and

3.4 濕熱環(huán)境對臨界載荷的影響

圖7 和圖8 給出了脫層情況一定(h2/h=0.5,L2/a=0.05)時(shí),不同溫度改變量ΔT(ΔC=0%)和濕度改變量ΔC(ΔT=0 ℃)下,脫層板的承載后屈曲路徑,其中ˉw為無量綱撓度。 根據(jù)上面的分析,受壓脫層板一旦發(fā)生擴(kuò)展,會在原載荷下迅速擴(kuò)展至破壞,因此圖7 和圖8 中各算例的后屈曲路徑曲線終止于對應(yīng)參數(shù)下的擴(kuò)展載荷值。 圖7 和圖8 標(biāo)注出了各種濕熱情況下的無量綱屈曲載荷值和無量綱擴(kuò)展載荷值,可以發(fā)現(xiàn),溫度和濕度的增加會極大影響脫層板的承載能力,較大的濕熱變形會明顯的降低脫層板的屈曲載荷、后屈曲強(qiáng)化載荷和臨界擴(kuò)展載荷。 同時(shí),不管處于何種濕熱場,脫層板都表現(xiàn)出后屈曲強(qiáng)化的特性;且隨著載荷增加,脫層板在屈曲后產(chǎn)生的面外變形不斷增加,導(dǎo)致層間剪力的不斷累積而發(fā)生Ⅱ型脫層擴(kuò)展。

圖7 溫度改變對無量綱臨界載荷和及后屈曲路徑的影響Fig.7 Effect of change of temperature on non-dimensional critical load and and post-buckling equilibrium path

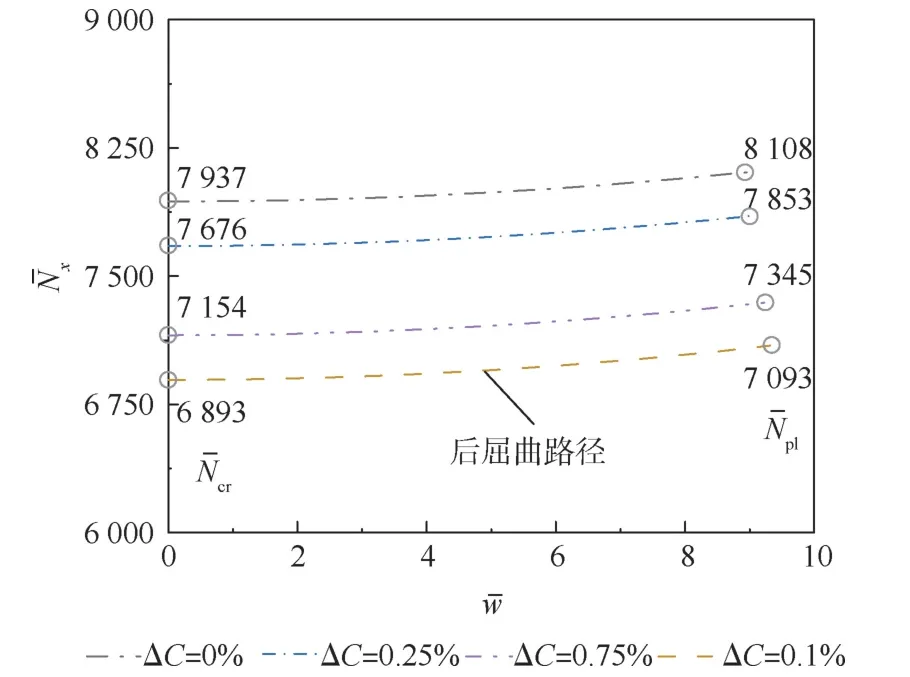
圖8 濕度改變對無量綱臨界載荷和及后屈曲路徑的影響Fig.8 Effect of change of hygroscopic concentration on non-dimensional critical load and and post-buckling equilibrium path

4 結(jié) 論

1) 經(jīng)典層合板理論由于忽略橫向剪切變形,高估了層合板的承載能力,計(jì)算的屈曲載荷和擴(kuò)展載荷均高于剪切理論的解。

2) 在同一濕熱場中,當(dāng)脫層深度越靠近層合板的中間位置或脫層長度越大時(shí),脫層越容易發(fā)生擴(kuò)展。 脫層擴(kuò)展是一個持續(xù)的過程,脫層擴(kuò)展導(dǎo)致脫層長度增加,脫層板的承載力隨之下降,脫層在原壓縮載荷下會繼續(xù)擴(kuò)展,直到層合板的完全破壞。

3) 濕熱變形會顯著降低脫層板的屈曲載荷、后屈曲載荷及擴(kuò)展載荷。 在不同濕熱場中,層合板都表現(xiàn)后屈曲強(qiáng)化的特性。