Tanabe 模型和Smith 熱調節模型結合預測皮溫效果分析

王濤, 張萬欣,*, 李猛, 卜雪琴, 張宸, 王海亮

(1. 中國航天員科研訓練中心人因工程重點實驗室, 北京 100094; 2. 北京航空航天大學 航空科學與工程學院, 北京 100191)

熱調節模型是人體內外傳熱的數學描述[1],其可對核心溫度和皮膚溫度等生理參數進行預測,為熱感覺和熱舒適評價模型提供輸入條件,因此,熱調節模型是熱感覺和熱舒適評價方法的組成部分[2]。 日常生活中人們經常處于各類室內環境中,了解人體對環境的熱感覺,評價環境的熱舒適程度是建筑暖通設計和節能的需要,由此促進了人體熱模型的發展。

人體熱調節模型始創于20 世紀初期,文獻[3]指出,1911 年提出了一個經驗模型把人體描述成一個節點與外環境傳熱。 1934 年Burton[4]創建了人體傳熱數學模型,模型中包括人體解剖結構和熱調節控制方程。 這些發展初期的人體熱模型無論是精度還是適用性都較差。 20 世紀60 ～90 年代,一些具有里程碑意義的模型相繼出現,如Gagge 兩節點模型[5]、文獻[6]所提模型和Smith 多元模型[7]等,2000 年后模型的發展多是在以上經典模型的思路框架下對模型中受控系統和熱調節系統進行的改進、完善和創新,并加快了模型應用研究。 2001 年Fiala 等[8]創建多節點模型,其受控系統模型把人體劃分為15 個節段,共187 個節點,描述了人體與外界對流、輻射、汗液蒸發等多種傳熱形式,考慮了衣物熱阻的影響,其在生理熱調節模型的建立上是通過試驗數據的回歸分析獲得的生理熱調控模型,該模型可以預測穩態和瞬態下人體整體和局部的生理熱響應。2001 年UC Berkeley 多節點模型[9-10]是以Stolwijk模型為基礎建立起來的,其受控系統模型可以把人體劃分為任意個節段,并考慮了身高、體重、肥胖和性別等個體生理和衣物穿著差異,模型將以上人因參數變量融合到人體生成器中,可以研究不同生理特征對人體熱響應的影響,其在生理熱調節模型的建立上主要用與設定點溫度進行比較,完成反饋和控制,該模型可以預測瞬態和非均勻下人體整體和局部的生理熱響應。 2002 年Tanabe 等[11]建立的多節點模型也是以文獻[6]所提模型為基礎,其受控系統模型把人體劃分為16 個節段,每個節段分為4 層共64 個節點,第65 個節點定義為中心血液,其與64 個節點進行對流傳熱,人體與外界通過對流、輻射、汗液蒸發等形式進行熱交換,在生理熱調節模型的建立上主要用與設定點溫度進行比較,完成反饋和控制,該模型可以預測瞬態和非均勻下人體整體和局部的生理熱響應。 2016 年Lai 和Chen[12]建立的多節點模型允許在不同節段上設置衣物熱阻,并在相鄰節段間增設了血液傳熱模擬;2018 年Davoodi等[13]在Gagge 兩節點模型上考慮體重、身高、性別、年齡和基礎代謝等個體因素發展出了個體化熱調節模型;2019 年Kang 等[14]創建的多節點模型在相鄰節段間模擬了導熱傳熱;2020 年范路[15]通過對大量文獻研究指出每種人體熱模型都有其適用范圍,需要根據實際應用加以修正,今后模型的改進將集中在血液模型、服裝模型、個體差異和特定環境模型的改進上。 人體熱模型的應用主要體現在熱舒適[16-19]、暖通[20]、醫療[21]、特種服裝[22]和暖體假人[23-24]等領域。

從經驗模型到兩節點模型,再到多元模型是一個由簡單到復雜的發展過程。 模型越復雜對人體劃分得越細致,越適合描述非均勻環境下的人體熱響應,但同時模型使用難度也越大,對計算機的運算和存儲能力要求也越高。 隨著計算機技術的普及應用,近30 年來人體熱模型得到快速發展。Tanabe[11]模型、Fiala[8]模型和Berkeley 模型[9-10]等都是較為成功的模型。 盡管如此,目前用于生理參數預測的人體熱模型還不能應用在熱舒適評價的國際標準中。 這是因為模型沒有統一公認的驗證規范,研究文獻中提供的試驗驗證方法和數據針對性強,無普適性。 這種狀況使得模型預測精度和可靠性受到質疑[25]。 因此,現階段人體熱模型距離成熟應用仍有較大距離,還需要進一步的理論創新研究來夯實基礎和試驗研究積累數據。

本文創建的人體熱調節模型在受控系統上采納了Tanabe[11]模型,按生理自然節段把人體分為65 個傳熱節點,每個節點的傳熱采用Pennes 生物熱方程,從傳熱學角度看Tanabe 模型對人體受控系統的劃分更直觀、簡便、合理,抓住了人體內部傳熱的主要特征。 但其在熱調節控制系統模型上采用與設定點溫度進行比較反饋控制,該方法簡單,個體差異對設定點溫度值影響大,反映到模型預測上就是可靠性不高,相比之下,Smith 多元模型中的生理熱調節模型是建立在大量人體解剖和生理數據基礎上,熱調節模型中的各類參數有其實際物理意義,更具客觀性,更能描述人體生理熱調節的客觀規律。 因此,采用這2 種模型的組合可以有助于提高人體熱調節模型的預測水平和可靠性,在學術和應用2 個方面體現出一定價值。2 種模型的組合在本文設定工況下對人體皮膚溫度的預測和試驗結果吻合度較高。

1 人體熱調節模型

人體熱調節模型可以分為受控系統模型和熱調節控制系統模型2 部分。 受控系統模型是描述各層肌體組織、血液循環系統、呼吸系統和皮膚層與外界的傳熱;熱調節控制系統模型用于描述人體應對外環境變化時肌體產生的熱調節生理功能,包含血液系統輸血量控制,皮膚血管舒縮引起的血流量變化控制,汗液分泌變化引起的蒸發散熱控制,寒顫引起的肌肉層代謝產熱控制。

1.1 受控系統模型

模型中的受控系統是從傳熱學角度對復雜人體組織的簡化劃分[11]。 依據人體結構特點將人體劃分為頭、胸、背、腹、上臂、下臂、手、大腿、小腿、足共16 個節段(下文用字母i∈[1,16]來指代身體各節段),每個節段沿徑向分成4 層:核心層、肌肉層、脂肪層和皮膚層(下文用字母j∈[1,4]來指代各組織層),外加一個中心血池,這樣人體就由65 節點構成。 如圖1 所示,各層組織間通過導熱形式傳遞熱量,組織層與血液循環系統發生的傳熱被簡化成與中心血池的傳熱,皮膚層與外環境間通過對流、輻射、蒸發和呼吸進行熱交換,其中呼吸傳熱僅限頭部和胸部。

圖1 人體受控系統傳熱原理Fig.1 Heat transfer schematic diagram of human passive system

利用Pennes 生物熱方程對4 個組織層和中心血池建立能量平衡方程:

式中:C為人體組織比熱容[11],(Wh)/℃;T為人體各層溫度,℃;τ為時間,s;Q為代謝產熱,W;B為血流傳熱,W;D為組織層間的導熱,W;RES 為呼吸傳熱,W;QT為皮膚層與外界的顯熱傳熱,W;E為皮膚層與外界的潛熱傳熱,W。1.1.1 代謝產熱計算

代謝產熱Q(i,j)計算如下:

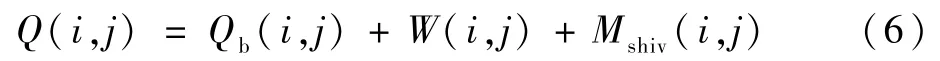
式中:Qb(i,j)為各組織層節點的基礎代謝率[11];W(i,j)為對外做功產熱;Mshiv(i,j)為寒顫產熱。做功產熱和寒顫產熱只發生在肌肉層(即j=2),其他層為0。

人體對外做功計算如下:

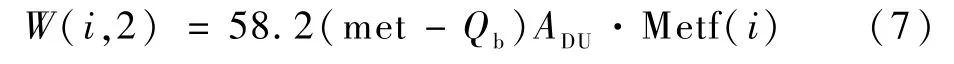
式中: met 為代謝當量( metabolic equivalent,MET),是一種表示運動強度的重要指標,1 met 定義為一個健康成年人靜坐保持舒適狀態時的新陳代謝率,約為58.15 W/m2;Qb為基礎代謝率,是人體節段各組織層節點基礎代謝的總和,約為0.778 met;Metf(i)[11]為對外做功引起的人體肌肉層產熱在每個節段上的分配系數;ADU為人體表面積,由Du Bois 公式計算,表示為

式中:W為人體體重,kg;H為人體身高,m。

1.1.2 血流傳熱計算

血流傳熱B(i,j)是中心血池與各組織層間的熱交換,其計算式如下:

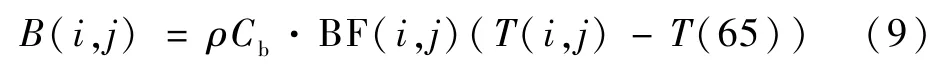
式中:ρCb為血液的體積比熱[11],ρ為密度,Cb為比熱;T(65)為中心血池溫度;BF(i,j)為血流量,核心層、肌肉層和脂肪層血流量,其計算式為

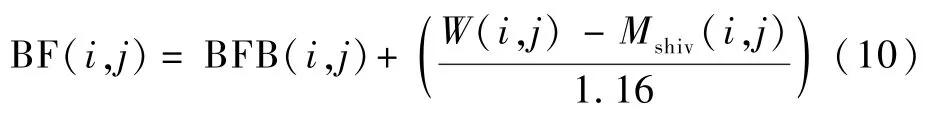
其中:BFB(i,j)為基礎血流;式(10)等號右邊第2項為代謝產熱引起的血流增加量[11]。

1.1.3 組織導熱計算

相鄰組織層間的導熱傳熱計算如下:

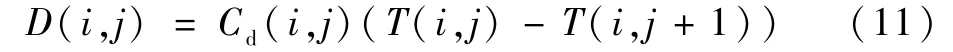
式中:Cd(i,j)為不同節段組織層的導熱系數[11]。1.1.4 呼吸散熱計算

人體的呼吸散熱發生在頭、胸部的核心層,即節點(1,1)和(2,1)處,RES(i,j)可表示為

式中:Ta為環境溫度,℃;Pa(1)為水蒸氣壓力,kPa。1.1.5 皮膚層與外界傳熱計算

皮膚層與外界散熱有兩部分組成:顯熱散熱QT(i,4)和蒸發散熱E(i,4),計算如下:

式中:λ為水的蒸發潛熱,取33 ℃對應值2 422 kJ/kg;ADU(i)為節段i的體表面積[11];Ta為環境溫度;P(i,4)和Pa分別為皮膚表面和環境水蒸氣分壓力,Pa;Rt,fab和Re,fab分別為衣物的熱阻和濕阻,單位 分 別 為(m2K)/W 和(m2Pa)/W;RTa和Rea分 別為皮膚外表面空氣層的熱阻和水汽阻力,單位分別為(m2K)/W 和(m2Pa)/W,計算式為[26]

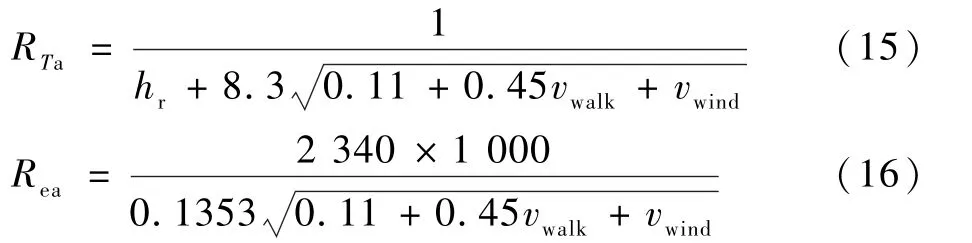
其中:hr為輻射傳熱系數,取5.0 W/(m2K);vwalk和vwind分別為步行速度和環境風速,m/s。

1.1.6 初始與邊界條件

邊界條件有環境溫度、環境水蒸氣分壓力、風速、衣物熱阻和濕阻等,均可通過試驗測量。 核心層、肌肉層、脂肪層的初始溫度參考文獻[21]中熱中性狀態下的設定值,皮膚層的初始溫度由試驗值給出。

皮膚層水蒸氣分壓力P(i,4)和人體出汗率相關。 根據Umeno[27]的建議,人體皮膚表面汗液的聚集量不會超過35 g/m2的極限值,如有超出部分將會從皮膚上滴落或被內層衣物吸濕帶走。在皮膚上的汗液聚集小于35 g/m2時,汗液聚集量等于出汗率加無感出汗減去汗液蒸發量,如下[28]:

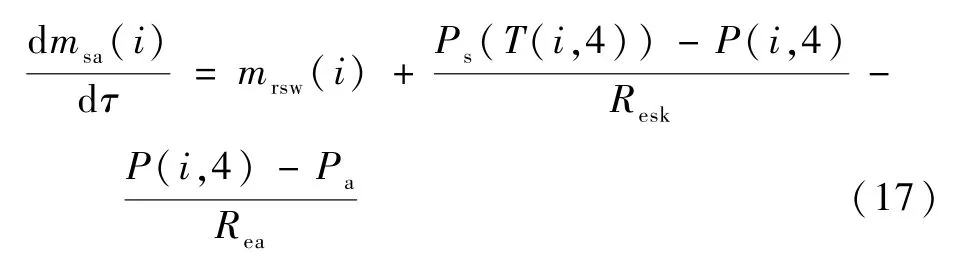
式中:msa(i)為第i節段皮膚層汗液聚集量,kg/m2;mrsw(i)為第i節段的出汗率,kg/(m2s);Resk為皮膚水蒸氣阻力,(m2Pas)/kg;Ps(T)為環境溫度Ta下的皮膚層飽和水蒸氣分氣壓,Pa,計算式為

人體皮膚上出現汗液聚集時,皮膚表層的水氣壓力P(i,4)等于溫度T(i,4)下的飽和水蒸氣壓力,在沒有汗液聚集時,可由式(17)推導計算。由此P(i,4)計算如下:

1.2 熱調節控制系統模型

熱調節控制系統[7]原理如圖2 所示。 人體皮膚層的溫度感受器反饋信號與體溫基準輸入信號的偏差作為體溫調節中樞的控制信號,控制調節肌肉寒顫、汗液分泌、血管舒縮或運動代謝來消除身體的冷熱應激,維持人體核心體溫和平均皮膚溫度處于正常工作范圍。

圖2 人體熱調節控制系統原理Fig.2 Schematic diagram of human thermoregulatory control system

人體熱調節控制方程涵蓋血管舒縮引起熱量輸送控制、汗液散熱控制和肌肉代謝產熱控制,反映了人體隨環境改變的自適應調節功能特點,是人體熱模型的重要組成部分。 本文采用Smith[7]基于試驗數據提出的熱調節控制系統模型。 模型中的控制變量為核心溫度Tcore和平均皮膚溫度Tskin,核心溫度取中心血池溫度T(65),平均皮膚溫度計算如下:

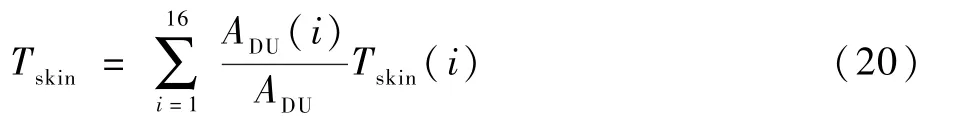
1.2.1 皮膚層血流量控制

皮膚層血管收縮時的血流量控制BFsk,con(i)計算如下:

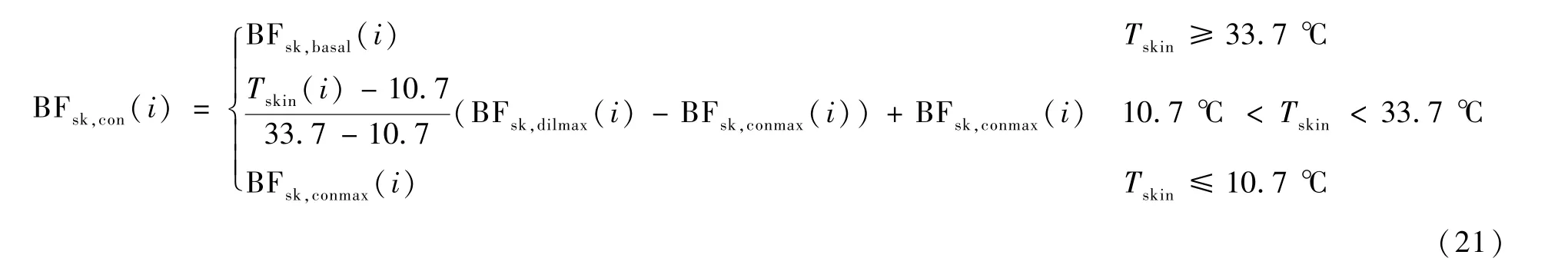
式中:BFsk,basal(i)為i節段皮膚層基礎血流量[7];BFsk,conmax(i)為i節段皮膚血管最大收縮狀態下的血流量[7]。

皮膚層血管舒張時的血流量控制BFsk,dil(i)為

式中:BFsk,dilmax(i)為i節段皮膚血管最大舒張狀態下的血流量[7]。

人體各節段皮膚層血流量計算如下:

式中:等號右邊第1 部分為人體耗氧量與熱中性狀態下耗氧量的比值,這說明血流量與人體運動耗氧成比例;VO2和VO2,basal分別為實時耗氧量體積和熱中性狀態下耗氧量體積,計算式為

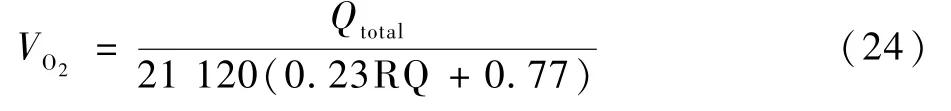
其中:Qtotal為總代謝率;RQ 為呼吸熵,定義為人體呼出二氧化碳體積流率與吸入氧氣體積流率的比值,熱中性狀態下其值約為0.77。1.2.2 出汗率控制

核心溫度Tcore超過了出汗閾值或37.1 ℃,人體會發生出汗現象。 出汗閾值Tsweat為平均皮膚溫度Tskin的函數,計算如下:

人體出汗率最大值不超過0. 193 3 g/s。 整個人體出汗率msw,計算如下:

人體各節段的出汗率mrsw(i) (單位為kg/(s·m2)),計算如下:

式中:Sweat(i)為每個節段出汗率的權重系數,是身體節段的汗腺數量與整個身體汗腺數量的比值[11]。

1.2.3 寒顫代謝產熱控制

平均皮膚溫度低于寒顫閾值Tshiv,則身體會發生寒顫現象,但當核心溫度Tcore等于或高于37.1 ℃時,無論平均皮膚溫度是多少,身體都不會發生寒顫。 人體發生寒顫的平均皮膚溫度閾值Tshiv計算如下:

寒顫代謝率Mshiv計算如下:

式中:Mshiv,max為寒顫引起的肌肉層最大代謝產熱率,是核心溫度的函數,計算式為

人體各節段肌肉層寒顫代謝產熱率Mshiv(i,2)的計算需要引入寒顫加權系數Shiv(i)[11],該系數是將寒顫代謝Mshiv分配到身體每一節段的肌肉層中。 各節段肌肉層寒顫代謝產熱計算如下:

2 試驗設計

考慮到在空調環境中的室內運動日益成為人們快節奏生活的選擇,試驗設計對此種情況設置了環境參數、運動工況,并對試驗誤差進行分析。

2.1 環境參數設置

根據常規室內空調環境,試驗設定的環境溫度、濕度、風速如表1 所示。 室內運動時穿著連體內衣,衣物整體熱阻和濕阻的測定值如表1所示。

表1 環境參數匯總Table 1 Environmental parameters

為保障環境參數的一致性,受試者進入恒溫艙完成上肢運動代謝流程,在此過程中采集人體皮膚溫度等參數,試驗現場照片如圖3 所示。

圖3 試驗現場受試者做功照片Fig.3 Photo of a subject working at test site

2.2 運動工況設置

運動工況依據代謝量大小涵蓋低強度活動量、中等強度活動量和高強度活動量。 低強度活動量下受試者做簡單的上肢運動,中等和高強度活動量下受試者操作上肢功率計對外做功。 做功代謝量級、做功時間和間歇期的設定值依據GB/T 18048—2008[29]。 運動設置對應人體代謝產熱量水平和運動工況信息如表2 所示。

表2 運動工況設置Table 2 Motion settings

2.3 誤差分析

試驗測量的物理量有溫度、濕度、流量、風速、質量和代謝量,相應的測量設備及精度信息如表3所示。肺功能儀用于實時采集人體吸入氧氣和呼出二氧化碳的體積流量,以此計算人體代謝產熱。計算方法如下:根據式(32)中的獨立測量參數:氧氣體積流量、二氧化碳體積流量、人體質量和人體身高,可以得到人體代謝產熱測量誤差,計算如下:

表3 試驗設備信息匯總Table 3 Experimental equipment

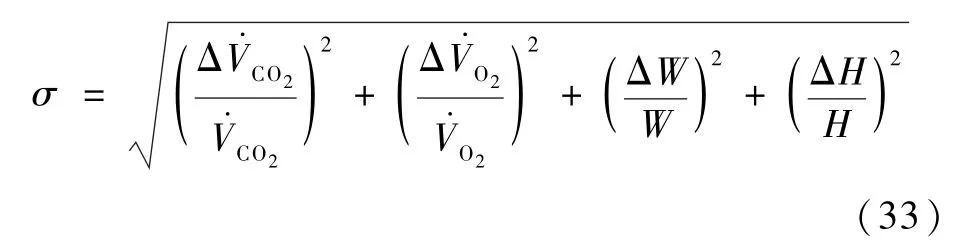
3 結果與分析

3.1 工況設置

受試者4 名,個人詳細信息如表4 所示。

表4 受試者信息Table 4 Profile of subjects

試驗中,受試者皮膚上貼附溫濕度傳感器,按規定著裝后進入恒溫室靜坐1 h,恒溫室溫度設置為25 ℃,濕度為50%,風速為0(按0. 2 m/s 取值),在此過程中采集熱中性狀態下皮膚溫度等生理參數,而后受試者如圖4 所示,依次進行靜立、肩運動、肘運動和操作上肢功率計對外20,30,40,60 W 做功。 受試者完成每一項運動用時4 min 左右,而后站立靜息7 min,運動全程記錄人體皮膚溫度和外環境參數,試驗中環境溫度為25.6 ℃,大氣相對濕度為54%。 人體周圍風速為0.7 m/s,大氣壓強為98.6 kPa。

圖4 人體運動做功流程Fig.4 Flow diagram of work by body movement

3.2 試驗結果

圖5 ～圖8 為4 名受試者運動過程中各節段皮膚溫度模擬計算值與試驗值的對比分析。

圖5(a)和圖5(b)分別為受試者1 和2 與受試者3 和4 平均皮膚溫度曲線和代謝產熱曲線。隨著對外做功負荷的增加,代謝產熱隨之升高,平均皮膚溫度逐漸上升。 受試者1 ～4 的平均皮膚溫度分別約為33.3 ℃、33 ℃、33.5 ℃和32.7 ℃。代謝產熱曲線顯示運動時人體產熱增加,休息時下降。 在做功60 W 時,受試者1 和2 達到代謝產熱約為6 met,受試者3 和4 達到代謝產熱約為3 met,代謝產熱的差別可能與年齡因素有關。4 名受試者平均皮溫的仿真值與試驗值最大誤差小于0.7 ℃。 圖6 為頭部皮膚溫度變化曲線。 曲線顯示整個運動過程中,頭部皮膚溫度無明顯變化,只在對外做功60 W 時略有增加。 這是因為頭部不參與做功,其上汗腺分布密集,汗液的潛熱散熱可及時將熱量散發到環境中。 4 名受試者頭部皮膚溫度仿真值與試驗值最大誤差均小于0.5 ℃。

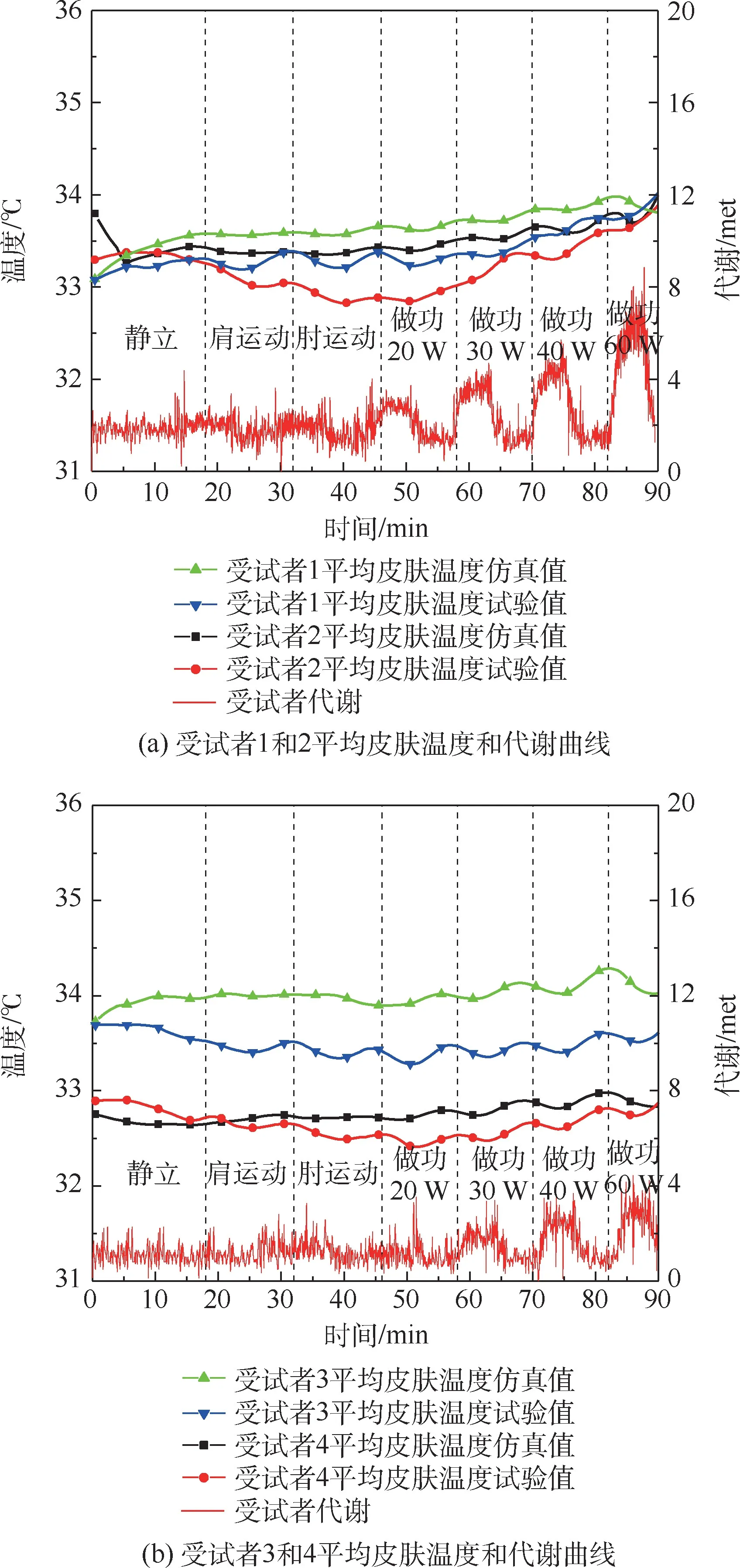
圖5 平均皮膚溫度曲線Fig.5 Mean skin temperature curves of bodies

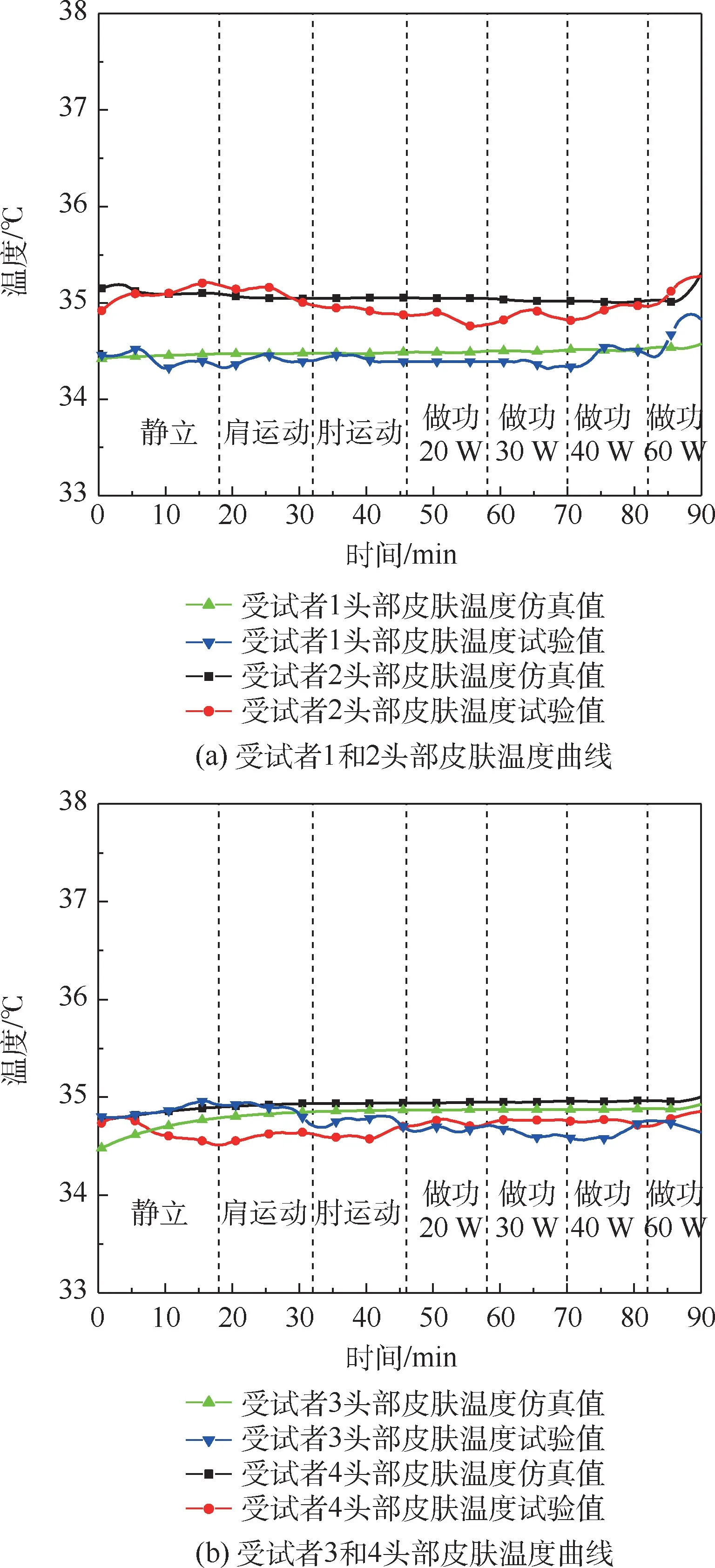
圖6 頭部皮膚溫度曲線Fig.6 Skin temperature curves of heads

圖7 為背部皮膚溫度曲線。 背部皮膚溫度隨上肢做功增加呈現上升趨勢,這是因為背部肌肉群對外做功,引起背部皮膚溫度升高。 在對外做功40 W 和60 W 的休息期間,受試者1 ～3 溫度迅速上升形成波峰說明背部肌肉群中的代謝產熱在做功完成后休息期間才傳遞到皮膚層,這揭示了人體組織傳熱具有滯后性。 受試者4 溫度較為平緩,是因為出汗降低了皮膚溫度。 4 名受試者背部皮膚溫度仿真值與試驗值最大誤差小于0.6 ℃。

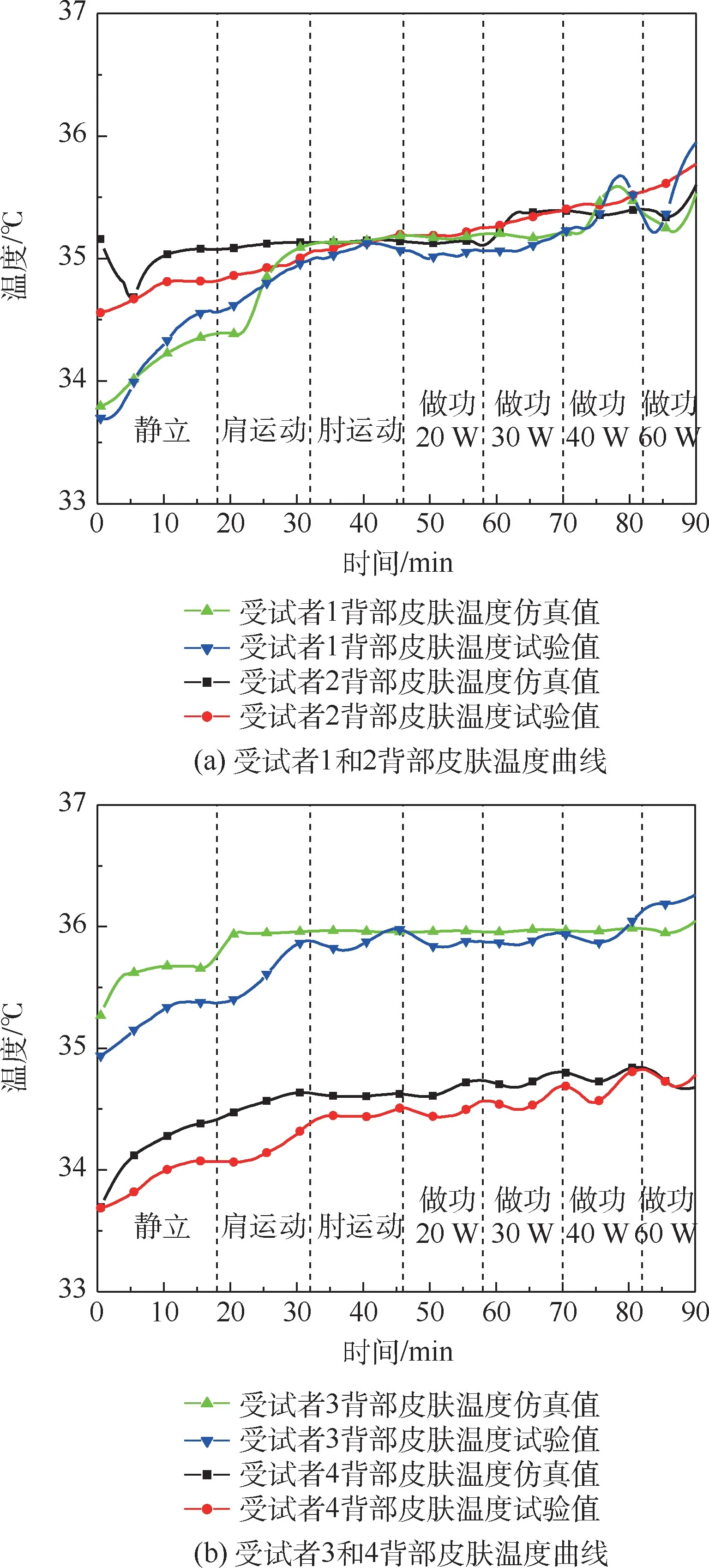
圖7 背部皮膚溫度曲線Fig.7 Skin temperature curves of backs

圖8 為胸部皮膚溫度曲線。 胸部皮膚溫度曲線隨著做功量增加呈現緩慢上升趨勢,說明胸部肌肉層代謝產熱與皮膚層對外散熱基本保持了平衡。 但在60 W 做功休息期間溫度有較明顯上升,是由于60 W 做功時胸部肌肉層代謝產熱速率顯著大于皮膚層散熱速率,又因為人體組織傳熱的滯后性使得皮溫的迅速增加出現在60 W 做功后。 4 名受試者胸部皮膚溫度仿真值與試驗值最大誤差小于0.7 ℃。

圖8 胸部皮膚溫度曲線Fig.8 Skin temperature curves of chests

圖9 為上臂溫度曲線。 上臂肌肉做功大,皮膚溫度上升顯著。 上臂皮膚溫度曲線有明顯的周期性波動—即在每個做功周期內,皮膚溫度先下降后升高(運動時下降,休息時升高),這是做功和停歇的周期性活動引起代謝和對流散熱變化而導致皮溫的周期性改變:運動時上臂與空氣間有較大的相對運動,空氣的對流傳熱大,皮溫下降;休息時對流散熱小,同時因人體傳熱的滯后性使得做功的代謝產熱休息期間釋放到皮膚表面引起皮溫增加。 4 名受試者1 號和2 號上臂皮膚溫度仿真值與試驗值最大誤差均小于0.8 ℃。

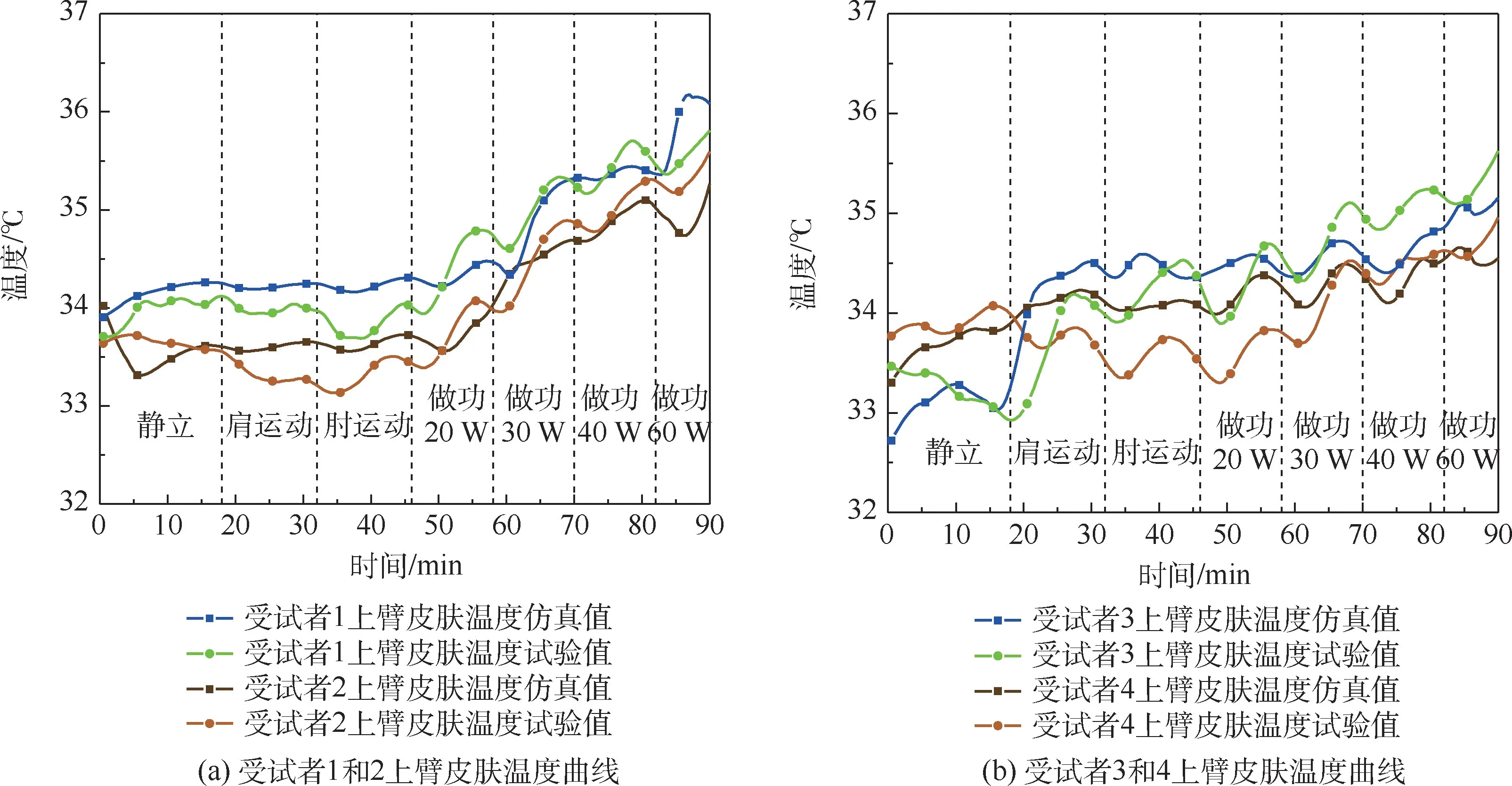
圖9 上臂皮膚溫度曲線Fig.9 Skin temperature curves of uper arms

圖10 為手部皮膚溫度曲線。 手部肌肉做功小,運動速度快,對流傳熱強,皮膚溫度上升趨勢弱。 手部皮膚溫度曲線有明顯的周期性波動—即在每個做功周期內,皮膚溫度先下降后升高(運動時下降,休息時升高),這是做功和停歇的周期性活動引起代謝和對流散熱變化而導致皮溫的周期性改變:運動時手部與空氣間有較大的相對運動,空氣的對流傳熱大,皮溫下降;休息時對流散熱小,同時因人體傳熱的滯后性使得做功的代謝產熱休息期間釋放到皮膚表面引起皮溫增加。 4 名受試者手部皮膚溫度仿真值與試驗值最大誤差均小于0.8 ℃。

圖10 手部皮膚溫度曲線Fig.10 Skin temperature curves of hands

圖11 為腿部皮膚溫度曲線。 腿部皮膚溫度曲線隨做功增加,呈現略微上升趨勢。 這是因為腿部離人體軀干近,做功產熱通過血液循環系統容易將熱量傳輸給腿部。 圖11 中溫度曲線在每個做功周期內表現出先下降后上升的波動性,也反應了人體代謝產熱在人體中傳遞滯后的特點。4 名受試者腿部溫度仿真值與試驗值最大誤差均小于0.5 ℃。

圖11 腿部皮膚溫度曲線Fig.11 Skin temperature curves of thighs

圖12 為腳部皮膚溫度曲線。 腳部代謝產熱小,離身體核心部位遠,其皮溫受外環境影響大,因此4 名受試者腳部皮膚溫度變化趨勢有不同。圖12 中30 W 以上對外做功周期內腳部皮膚溫度有較為明顯波動,說明上肢中高強度周期性做功(30 W 以上)產熱通過血液系統對腳部皮溫會產生一定影響。 4 名受試者腳部溫度仿真值與試驗值最大誤差小于0.5 ℃。

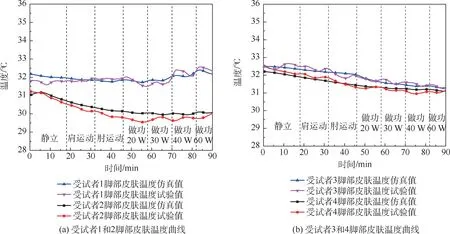
圖12 腳部皮膚溫度曲線Fig.12 Skin temperature curves of feet

圖7 背部和圖8 胸部皮膚溫度曲線在起始段仿真與試驗相比有較大偏差,隨著時間變化偏差量逐漸減小,是由于各層組織初始仿真溫度的設定與試驗值存在偏差,隨著計算迭代次數的增加,各層溫度的仿真值與試驗值逐步趨近。

4 結 論

1) 人體上肢運動代謝產熱主要在上肢、背部和胸部相關肌肉群產生。 肌肉層中的代謝產熱在人體中的傳遞表現出滯后性。

2) 上肢運動代謝產熱對人體上部軀體產生的影響作用大于下部軀體。 頭部、背部和胸部皮膚溫度在中低負荷運動下變化不明顯,與這些部位汗腺分布密集散熱能力強有關。

3) 上肢運動代謝產熱通過血液系統傳遞到遠端肢體手和足的份額小,對手和足皮膚溫度影響弱。

4) 模型對各部位皮膚溫度的仿真值與試驗值吻合度較高,最大偏差量小于0.8 ℃。 誤差主要來源有以下5 個方面:①人體核心層、肌肉層和脂肪層溫度的初始值無法測量,其值引用了相關文獻數據,與真實值存在偏差;②人體模型中皮膚層節點溫度代表一個部位整個皮膚層溫度,而試驗中的皮膚測點溫度只是局部皮膚點溫度,二者實質物理含義不同,只是作為近似處理;③溫度傳感器與皮膚間有接觸熱阻,而且運動時會產生相對滑動,并伴有氣流影響,所以測試值與真實值存在偏差;④人體熱模型發展不完備,模型中內置的各類物性參數和控制參數對真實物理過程的反映有一定誤差;⑤模型對衣物在人體向外環境散熱中的作用進行了簡化處理,即用恒定的衣物熱阻和濕阻的測量值來描述衣物在散熱環節的阻力作用。 這樣的簡化雖然對吸濕性小的纖維制做的服裝是合理的,但簡化處理將不可避免的引入誤差。

綜上所述,本文中將Tanabe 模型與Smith 模型中基于試驗獲取的人體熱調節控制經驗方程相結合,再通過合理簡化衣物熱模型,設置各類物性參數、控制參數和邊界初始條件,進而抓住了人-服-環境系統熱質傳遞的主要特征和機理。 模型對試驗設置的常溫環境下中高強度運動中人體皮膚溫度的熱響應具有一定的預測能力。