面向控制的仿鴿撲翼機(jī)縱向動力學(xué)建模與分析

彭程, 孫立國, 王衍洋, 譚文倩, 肖峰

(北京航空航天大學(xué) 航空科學(xué)與工程學(xué)院, 北京 100191)

與一般的固定翼飛機(jī)相比,基于撲翼飛行生物仿生學(xué)設(shè)計(jì)的撲翼飛行器具有結(jié)構(gòu)簡單、質(zhì)量輕、飛行機(jī)動性和靈活性強(qiáng)及氣動效率高等優(yōu)勢,因此,仿生撲翼飛行器的研究已成為世界各國研究的熱點(diǎn)[1]。 根據(jù)尺寸大小、翅膀撲動的頻率及升力產(chǎn)生機(jī)理的不同,撲翼飛行器包括仿昆蟲型和仿鳥型2 種類型撲翼機(jī)。 本文研究的仿鴿撲翼機(jī)屬于仿鳥型撲翼機(jī)[2]。 仿鳥型撲翼飛行器尺寸較大,范圍從厘米級到米級不等,其機(jī)翼撲動頻率不高,小型鳥類一般不超過20 Hz,大型鳥類可能只有1 ～2 Hz,且其機(jī)翼相對于整個飛行器的質(zhì)量占比較大。 仿鳥型撲翼機(jī)主要以平飛運(yùn)動為主,其升力來源于機(jī)翼的撲動與空氣的相對運(yùn)動,此外,其機(jī)翼撲動在產(chǎn)生升力的同時還為其提供飛行的推動力[3-4]。

撲翼飛行器具有復(fù)雜的氣動特性[3],想要建立精確的動力學(xué)模型非常困難。 面向控制問題建模時雖對精度要求有所降低,但仍具有較高難度,目前仍缺少一個通用模型,在能反映機(jī)翼運(yùn)動產(chǎn)生的慣性力和力矩影響的同時,還能用于控制器設(shè)計(jì)的驗(yàn)證。 目前,撲翼飛行器的建模主要有2類方法。 一類是較為常用的采用了單剛體假設(shè)的牛頓-歐拉法[5-10]。 這種方法將撲翼飛行器視為質(zhì)量分布均勻的單剛體模型,不考慮機(jī)翼撲扭運(yùn)動產(chǎn)生的慣性力和慣性力矩。 另一類建模方法是將撲翼飛行器視為一個相對運(yùn)動約束下的多剛體模型[11-13],考慮機(jī)翼運(yùn)動時產(chǎn)生的慣性力和慣性力矩。 Orlowski 和Girard[12]的研究結(jié)果顯示,當(dāng)機(jī)翼相對于整個飛行器的質(zhì)量占比達(dá)到5. 7%時,撲翼機(jī)的單剛體近似模型與非線性多剛體模型的慣性位置、俯仰角和俯仰角速率的仿真結(jié)果差別較大,此時多剛體模型更精確。 此外,要建立能用于控制器設(shè)計(jì)的動力學(xué)模型,還需要獲取相關(guān)的氣動系數(shù)、氣動導(dǎo)數(shù)和操縱導(dǎo)數(shù)。 Dietl 和Garcia[8]利用Andersen 等[14]使用氣動數(shù)據(jù)計(jì)算得到的氣動導(dǎo)數(shù)和操縱導(dǎo)數(shù),建立了撲翼飛行器面向控制的縱向動力學(xué)模型。 Kajak 等[9]利用最小二乘法估計(jì)得到了相關(guān)的氣動系數(shù)和操縱導(dǎo)數(shù),建立了無尾撲翼飛行器面向控制的縱向動力學(xué)模型。 Jiang 等[10]進(jìn)一步考慮了尾翼的影響,利用Sun 等[15]給出的氣動系數(shù)和氣動導(dǎo)數(shù)及Armanini等[16]給出的操縱導(dǎo)數(shù)建立了撲翼飛行器面向控制的縱向動力學(xué)模型。 在撲翼飛行器建模的研究中[5-13],Kajak[9]和Jiang[10]等建立的模型屬于仿昆蟲型撲翼機(jī),Dietl 和Garcia[8]建立的撲翼機(jī)尺寸雖然較仿昆蟲型撲翼機(jī)大,但是其使用氣動模型的雷諾數(shù)較低,適用于仿昆蟲型撲翼機(jī)。對于仿鳥型撲翼機(jī),目前還缺少相關(guān)的氣動導(dǎo)數(shù)和操縱導(dǎo)數(shù)數(shù)據(jù)。 因此,在考慮機(jī)翼運(yùn)動慣性力和慣性力矩影響的基礎(chǔ)上,如何建立仿鳥型撲翼機(jī)面向控制的縱向動力學(xué)模型仍然是一個需要解決的問題。

為給仿鳥型撲翼機(jī)控制算法的研究提供設(shè)計(jì)驗(yàn)證平臺,仍有待于從自然界鳥類的操縱機(jī)理來對仿鳥型撲翼機(jī)的動力學(xué)模型進(jìn)行拓展。 結(jié)合撲翼飛行生物和微型飛行器的飛行特點(diǎn),撲翼飛行器往往需要能夠改變俯仰力矩的操縱機(jī)構(gòu)來維持或改變俯仰姿態(tài)。 例如,李智[6]、Dietl 和Garcia[8]、Jiang 等[10]、年鵬等[17]采用升降舵的偏轉(zhuǎn)角作為輸入來改變俯仰力矩,Kajak 等[9]采用壓力中心的水平位置來改變俯仰力矩。 此外,撲翼飛行器還需要以機(jī)翼的撲動速度作為輸入來改變飛行時的推力,其中機(jī)翼在一個撲動周期內(nèi)的平均撲動速度可以通過控制機(jī)翼的撲動角振幅[6,8]、撲動角位移[17]、撲動頻率[6,9,18]等來改變。 然而,自然界中的鳥類在飛行中除了通過偏轉(zhuǎn)尾翼來維持縱向姿態(tài)平衡及改變翅膀的撲動振幅或頻率來改變飛行推力外,還會扭轉(zhuǎn)翅膀來配合翅膀的撲動,以調(diào)節(jié)翅膀產(chǎn)生的升力方向。 但是,目前針對包含機(jī)翼扭轉(zhuǎn)角振幅的面向控制的三輸入仿鳥型撲翼飛行器縱向動力學(xué)模型仍有待于研究。

綜上所述,為給仿鳥型撲翼機(jī)控制律設(shè)計(jì)提供通用驗(yàn)證平臺,本文建立了三輸入定撲動周期的仿鴿撲翼機(jī)線性時變周期系統(tǒng)模型,并進(jìn)行了動穩(wěn)定性分析和開閉環(huán)時域仿真分析等多角度的驗(yàn)證。 首先,考慮機(jī)翼運(yùn)動產(chǎn)生的慣性力和慣性力矩的影響,利用Kane 方程建立了仿鴿撲翼機(jī)的多剛體非線性模型;其次,選擇升降舵偏轉(zhuǎn)角、機(jī)翼撲動角振幅和機(jī)翼扭轉(zhuǎn)角振幅作為控制輸入,結(jié)合已有氣動數(shù)據(jù)及計(jì)算模型[19-22]工程估算了撲翼機(jī)的氣動導(dǎo)數(shù)系數(shù)和操縱導(dǎo)數(shù)系數(shù),建立了面向控制的仿鴿撲翼機(jī)縱向多余度線性時變周期系統(tǒng)模型;然后,基于Floquet 理論對該線性時變周期系統(tǒng)模型進(jìn)行了動穩(wěn)定性分析;最后,在設(shè)計(jì)基礎(chǔ)控制器和控制分配方法的前提下,進(jìn)行了開環(huán)和閉環(huán)仿真分析驗(yàn)證,闡釋了模型的可信性及機(jī)翼扭轉(zhuǎn)角振幅的引入對飛行操控能力的改善效果。

1 仿鴿撲翼機(jī)線性時變周期系統(tǒng)模型的建立

1.1 仿鴿撲翼機(jī)的多剛體模型

仿鴿撲翼機(jī)模型包含機(jī)身、一對對稱的機(jī)翼和尾翼。 機(jī)翼通過鉸鏈與機(jī)身相連接,繞xb軸上下?lián)鋭?同時繞機(jī)翼中心線扭轉(zhuǎn)運(yùn)動,撲動角為φ,扭轉(zhuǎn)角為η,如圖1 所示。

圖1 仿鴿撲翼機(jī)概念示意圖Fig.1 Diagram of a pigeon-like flapping-wing aircraft

仿鴿撲翼機(jī)穩(wěn)定飛行時,機(jī)翼的撲動和扭轉(zhuǎn)運(yùn)動是周期性的,為了方便表示機(jī)翼的運(yùn)動規(guī)律,參照Dietl 和Garcia[7]的方法將機(jī)翼撲動和扭轉(zhuǎn)分別簡化為頻率為f1和f2的正弦運(yùn)動:

式中:A為機(jī)翼撲動角振幅;R為機(jī)翼扭轉(zhuǎn)角振幅;t為時間;φ1和φ2分別為撲動和扭轉(zhuǎn)的相位角。

由于自然界中鴿子身體、翅膀的形狀極不規(guī)則且在飛行中不斷變化,要獲取其精確的外形幾何數(shù)據(jù)非常困難,為了方便分析,參照Orlowski 和Girard[12]的簡化方法,考慮機(jī)翼撲動產(chǎn)生的附加慣性力和慣性力矩的影響,將撲翼機(jī)簡化為圖2所示的多剛體模型。 機(jī)身簡化為一個質(zhì)量均勻的圓柱體,長度為l,半徑為r;左右機(jī)翼的形狀簡化為矩形,機(jī)翼展長為l1,單機(jī)翼質(zhì)心到機(jī)身尾翼組合體質(zhì)心距離為l2,單機(jī)翼弦長為l3;尾翼簡化為矩形薄板,單個尾翼長、寬分別為l4、l5,左右兩邊尾翼作為仿鴿撲翼機(jī)的升降舵,由聯(lián)動機(jī)構(gòu)連接,同時偏轉(zhuǎn)相同角度;機(jī)身尾翼組合體、左側(cè)機(jī)翼、右側(cè)機(jī)翼的質(zhì)量分別為m1、m2、m3,其中m2=m3,機(jī)翼質(zhì)心位于機(jī)翼幾何中心,機(jī)身質(zhì)心到機(jī)翼前緣的距離為xg,全機(jī)總質(zhì)量為m,其中m1、m2和m3前“*”表示重心位置。 需要說明的是,由于在較低的飛行速度下鳥類飛行的升力和推動力主要由翅膀撲動產(chǎn)生,為了方便分析,主要考慮仿鴿撲翼機(jī)機(jī)翼撲動產(chǎn)生的氣動力而忽略機(jī)身的氣動力,因此,由機(jī)身形狀的不同而產(chǎn)生的對全機(jī)氣動力的影響可以忽略。

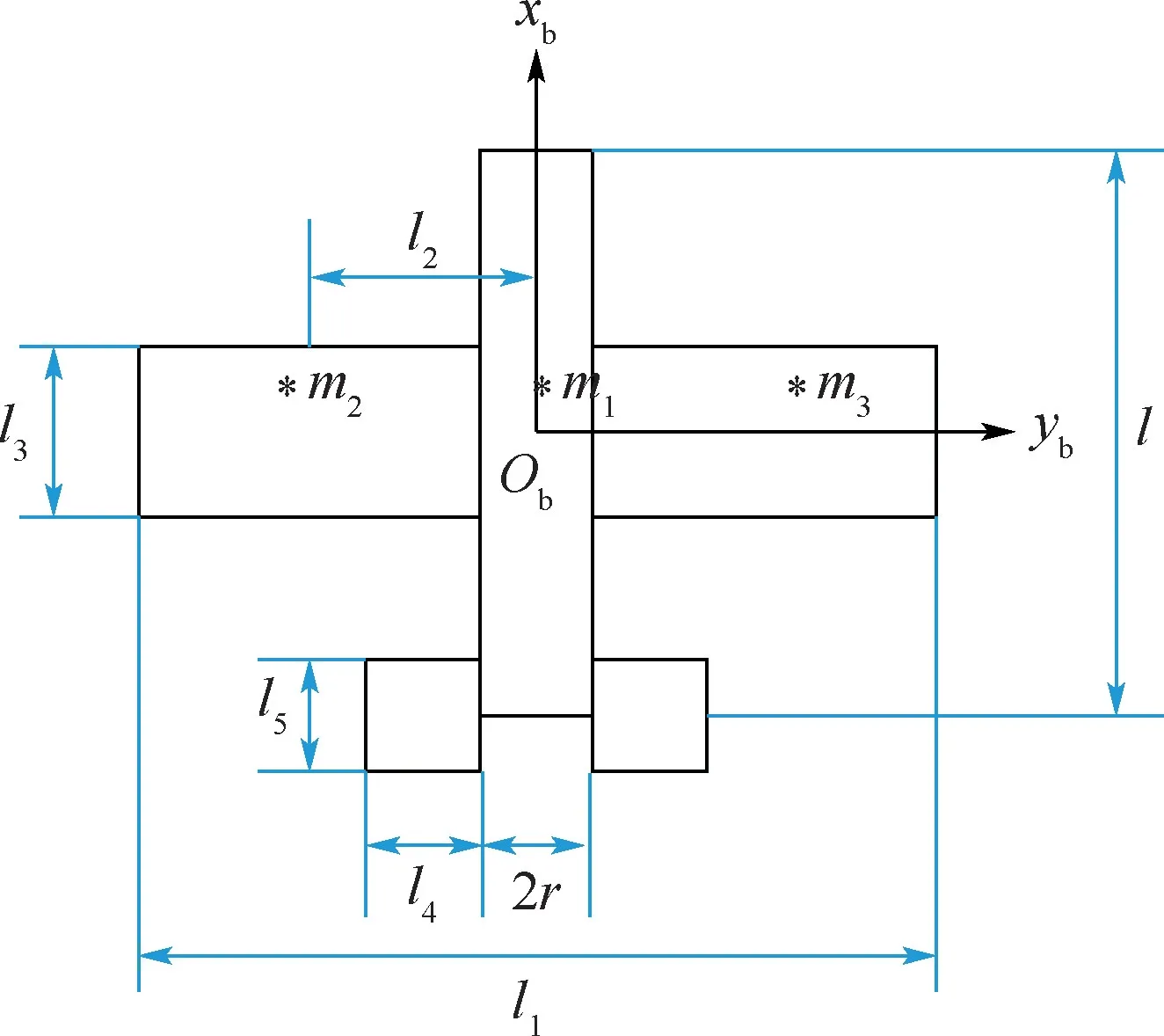
圖2 仿鴿撲翼機(jī)簡化模型Fig.2 Simplified model of pigeon-like flapping-wing aircraft

由于采用Kane 方程可以避免方程中出現(xiàn)對靜矩的求導(dǎo)項(xiàng),容易將動力學(xué)方程化為標(biāo)準(zhǔn)形式,便于編程計(jì)算[23],采用Kane 方程建立如式(3)所示的仿鴿撲翼機(jī)縱向多剛體動力學(xué)模型:

式中:u、w分別為撲翼機(jī)相對于地面參考系的速度在機(jī)體軸xb、zb方向的分量;q為撲翼機(jī)相對于地面參考系的俯仰角速度在機(jī)體軸上的分量,˙q、¨q分別為導(dǎo)數(shù)和二階導(dǎo)數(shù);θ為撲翼機(jī)相對于地面坐標(biāo)系的俯仰角;α為撲翼機(jī)飛行迎角;L、D、My分別為撲翼機(jī)所受的升力、阻力、俯仰力矩,其與撲翼機(jī)飛行速度V、雷諾數(shù)、撲翼機(jī)飛行迎角α及機(jī)翼撲動時的平均迎角αw有關(guān);I1y為機(jī)身在yb軸上的慣性矩,I2y為機(jī)翼在yb軸上的慣性矩。

該撲翼機(jī)模型的幾何參數(shù)和機(jī)翼運(yùn)動參數(shù)如表1 所示。

表1 仿鴿撲翼機(jī)幾何參數(shù)Table 1 Geometry parameters of pigeon-like flapping-wings aircraft

當(dāng)撲 翼 固 定 時,φ=η===== 0,式(3)為傳統(tǒng)的固定翼飛機(jī)的縱向動力學(xué)方程,與其相比較,式(3)中包含和的項(xiàng)為機(jī)翼撲動引起的慣性力或力矩,包含¨η的項(xiàng)為機(jī)翼扭轉(zhuǎn)引起的慣性力矩,多出來的其他項(xiàng)為機(jī)身運(yùn)動引起的機(jī)翼產(chǎn)生的慣性力或力矩。

1.2 仿鴿撲翼機(jī)操縱機(jī)制

為闡明仿鴿撲翼機(jī)的操縱機(jī)制及設(shè)計(jì)依據(jù),一方面,選取常規(guī)的升降舵偏轉(zhuǎn)角作為操縱輸入;另一方面,為了方便工程實(shí)踐和系統(tǒng)建模分析,在定周期條件下選取機(jī)翼撲動角振幅和扭轉(zhuǎn)角振幅作為操縱輸入。 其中,升降舵偏轉(zhuǎn)的變化可以通過伺服舵機(jī)電壓的變化來工程實(shí)現(xiàn);定周期下的機(jī)翼撲動角和扭轉(zhuǎn)角振幅的實(shí)時變化可以通過無刷電動機(jī)、伺服舵機(jī)和無級調(diào)幅撲翼驅(qū)動機(jī)構(gòu)[24]來工程實(shí)現(xiàn)。

本節(jié)以機(jī)翼撲動角為例,闡釋仿真中定周期、變振幅的機(jī)翼撲動角在各離散采樣時刻的實(shí)時變化情況。 在各個離散的采樣時刻,機(jī)翼撲動角的變化如下:

即在t=tk時刻,機(jī)翼撲動角位于振幅為(A0+ΔAk)的正弦軌跡線上。 以撲動頻率10 Hz,撲動基準(zhǔn)角振幅A0,仿真步長0.005 s,初始相位φ1=0 為例,機(jī)翼撲動角在一個周期為20 個離散采樣點(diǎn)的變化曲線如圖3 所示。

圖3 中,機(jī)翼撲動角在一個周期T內(nèi)的各采樣時刻點(diǎn)的值如下:

圖3 分時段變振幅撲動序列示意圖Fig.3 Diagram of flapping sequence of time-varying amplitude

1.3 面向控制的線性時變周期系統(tǒng)模型的建立

為了方便后續(xù)線性時變周期系統(tǒng)的分析及控制系統(tǒng)的設(shè)計(jì),本文對撲翼機(jī)非線性運(yùn)動方程(3)解耦并進(jìn)行小擾動線性化。 選擇仿鴿撲翼機(jī)升降舵的偏轉(zhuǎn)角變化量Δδe、機(jī)翼撲動角振幅相對于基準(zhǔn)值的變化量ΔA及機(jī)翼扭轉(zhuǎn)角振幅相對于基準(zhǔn)值的變化量ΔR來作為被控對象的控制輸入,即控制輸入為v= [ΔδeΔAΔR]T;撲翼機(jī)縱向狀態(tài)量相對于配平值的偏差為x=[uwqθ]T;選定速度為10 m/s、高度為20 m表示基準(zhǔn)飛行狀態(tài),在基準(zhǔn)飛行狀態(tài)下的配平值如表2所示。

表2 配平值Table 2 Trimming values

最終得到撲翼機(jī)的線性狀態(tài)方程:

式中:

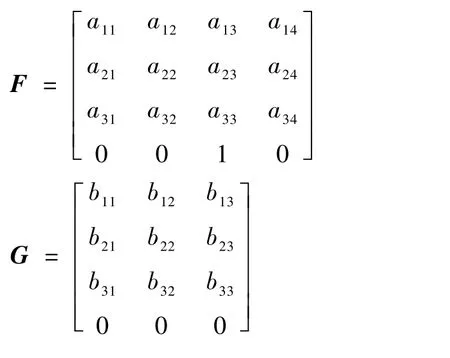
F中各元素由氣動系數(shù)和氣動導(dǎo)數(shù)構(gòu)成,在氣動系數(shù)方面F中各元素與升力系數(shù)CL、阻力系數(shù)CD和俯仰力矩系數(shù)Cm有關(guān),在氣動導(dǎo)數(shù)方面,a11、a21、a31與升力、阻力、俯仰力矩對速度u的導(dǎo)數(shù)Lu、Du、Mu有關(guān),a12、a22、a32與升力、阻力、俯仰力矩對速度w的導(dǎo)數(shù)Lw、Dw、Mw有關(guān),a13、a23、a33與升力、阻力、俯仰力矩對角速度q的導(dǎo)數(shù)Lq、Dq、Mq有關(guān)。G中各元素由操縱導(dǎo)數(shù)構(gòu)成,其中b11、b21、b31與升力、阻力、俯仰力矩對升降舵偏轉(zhuǎn)角δe的導(dǎo)數(shù)Lδe、Dδe、Mδe有關(guān),b12、b22、b32與升力、阻力、俯仰力矩對機(jī)翼撲動角振幅A的導(dǎo)數(shù)LA、DA、MA有關(guān),b13、b23、b33與升力、阻力、俯仰力矩對機(jī)翼扭轉(zhuǎn)角振幅R的導(dǎo)數(shù)LR、DR、MR有關(guān)。F和G中各元素的具體表達(dá)式可以通過小擾動線性化推導(dǎo)得到。 為獲取F和G隨機(jī)翼運(yùn)動的周期變化情況,本節(jié)將對仿鴿撲翼機(jī)的氣動系數(shù)、氣動導(dǎo)數(shù)系數(shù)及操縱導(dǎo)數(shù)系數(shù)進(jìn)行計(jì)算。

1.3.1 總氣動系數(shù)計(jì)算

特定撲翼翼型下的CL、CD、Cm大小與雷諾數(shù)Re、撲翼機(jī)飛行迎角α、機(jī)翼撲動時的平均迎角αw有關(guān),而αw又與α、A、f1、R、f2、機(jī)翼尺寸大小及撲動扭轉(zhuǎn)相位有關(guān)。 因此,CL、CD、Cm的大小由Re、α、A、R、f1、f2、t及機(jī)翼尺寸大小等元素共同確定。 由于仿鴿撲翼機(jī)的尺寸大小、飛行速度、Re與DOVE 撲翼機(jī)[25]基本相似,采用與DOVE 撲翼機(jī)相同的NACA4408 撲翼翼型,并結(jié)合其在Re為70 000 時CL、CD、Cm隨迎角的變換規(guī)律[20]和夏風(fēng)[19]給出的計(jì)算模型,計(jì)算得到各個采樣時刻機(jī)翼運(yùn)動產(chǎn)生的CL、CD、Cm大小。 在表2 中選定的基準(zhǔn)飛行狀態(tài)及表3 設(shè)定的基準(zhǔn)機(jī)翼運(yùn)動參數(shù)下,即Re、α、f1、f2均已設(shè)為定值,此時可以獲得在不同的A和R下,撲翼機(jī)的CL、CD、Cm在撲動周期內(nèi)的變化,其變化情況如圖4 和圖5 所示。

圖4 不同機(jī)翼撲動角振幅下氣動系數(shù)的變化Fig.4 Variation of aerodynamic coefficients with different amplitudes of flapping-wing angle

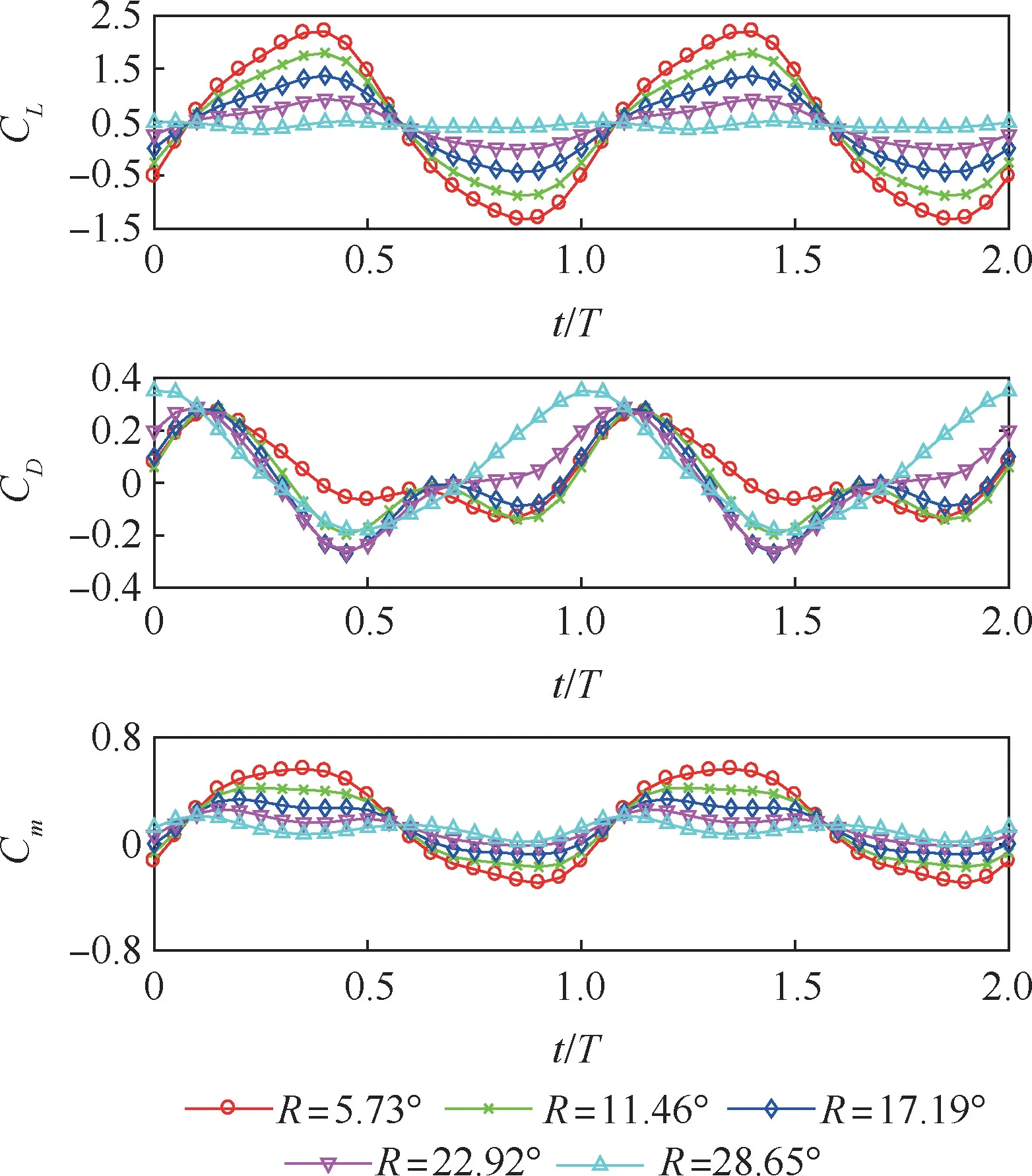
圖5 不同機(jī)翼扭轉(zhuǎn)角振幅下氣動系數(shù)的變化Fig.5 Variation of aerodynamic coefficients with different amplitudes of wing torsional angle

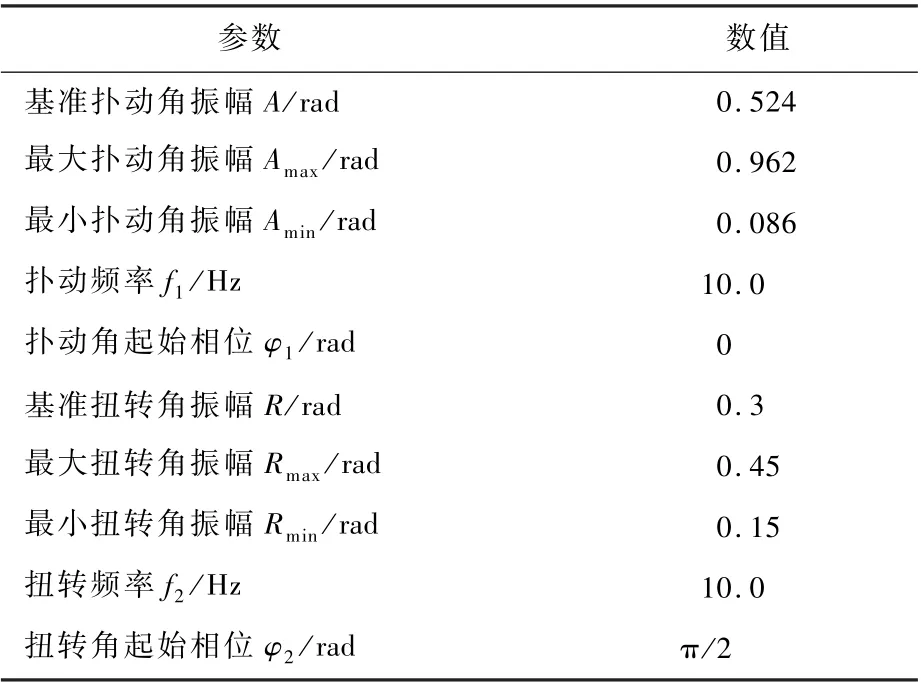
表3 機(jī)翼運(yùn)動參數(shù)Table 3 Motion parameters of wings

由圖4 可以看出隨著A的增大,撲翼機(jī)的CL、CD、Cm的振幅增大,CD的平均值減小,即推力的平均值增大,這與自然界中鳥類的飛行特點(diǎn)相符合。 此外,在A=15°時CL、CD、Cm變化較為平緩,且CL的變化趨勢與其他3 個不同角振幅下的變化趨勢相反,這是因?yàn)榻钦穹^小時機(jī)翼的撲動速度減慢,此時機(jī)翼的迎角主要受到扭轉(zhuǎn)的影響。 另外如圖5 所示,當(dāng)R增大時,CL的振幅減小,Cm的振幅也減小。 因此,可以期望通過調(diào)節(jié)R來減緩撲翼機(jī)飛行中由于CL和Cm的變化引起的θ的振蕩和最大的法向過載。 此外,R不能無限增大。 當(dāng)R過大時,會造成機(jī)翼撲動時迎角方向反向,從而造成升力反向,使飛行不穩(wěn)定。 由圖5可以看出R=28.65°時CL已經(jīng)開始出現(xiàn)反向,因此A=30.03°時,R不宜超過28.65°。 圖4和圖5 中T為周期,1T=0.1 s。

1.3.2 氣動導(dǎo)數(shù)系數(shù)和操縱導(dǎo)數(shù)系數(shù)估算

由于仿鴿撲翼機(jī)的平尾布局和作用與常規(guī)布局飛機(jī)類似,可以采用常規(guī)布局飛機(jī)的飛行動力學(xué)[21]對其進(jìn)行估算。 其中,平尾尾容比Aht、平尾力臂lht及平尾升力線斜率CLα,t等參數(shù)將直接影響氣動導(dǎo)數(shù)系數(shù)和操縱導(dǎo)數(shù)系數(shù)的大小,因此,選取合適的Aht、lht/ˉc(ˉc為平均氣動弦長)及CLα,t至關(guān)重要。

本文中的仿鴿撲翼機(jī)取Aht= 0. 37,lht/ˉc=1.67,對比表4 的撲翼機(jī)平尾容量系數(shù)典型值可以知道其Aht和lht/ˉc的大小均在合理范圍內(nèi)。 平尾翼型參考熊超[22]使用的尾翼翼型,其CLα,t=2.92,效率系數(shù)ηe=0.85。 基于Aht和lht/ˉc的數(shù)值大小及平尾的翼型和形狀,可以估算得到仿鴿撲翼機(jī)的氣動導(dǎo)數(shù)系數(shù)和升降舵的操縱導(dǎo)數(shù)系數(shù)。 此外,分別由圖4 和圖5 中的曲線插值可以得到A和R的操縱導(dǎo)數(shù)系數(shù)。 本節(jié)給出了氣動導(dǎo)數(shù)系數(shù)和操縱導(dǎo)數(shù)系數(shù)的估算方法及重要參數(shù)的選取依據(jù),進(jìn)而可以得到氣動導(dǎo)數(shù)系數(shù)和操縱導(dǎo)數(shù)系數(shù)的具體數(shù)值。

表4 撲翼機(jī)尾容量系數(shù)典型值[22]Table 4 Typical values of tail capacity coefficient of flapping-wing aircraft[22]

至此,獲得了仿鴿撲翼機(jī)線性模型中所需的氣動系數(shù)、氣動導(dǎo)數(shù)系數(shù)及操縱導(dǎo)數(shù)系數(shù),構(gòu)建了一個完整的面向控制的線性時變周期系統(tǒng)模型。

1.3.3 狀態(tài)矩陣特征值分析

在如式(6)所示的仿鴿撲翼機(jī)線性時變周期系統(tǒng)中,狀態(tài)矩陣F的特征值變化及短周期阻尼比和自振頻率變化情況如圖6 所示,其中,T為周期,1T=0.1 s。

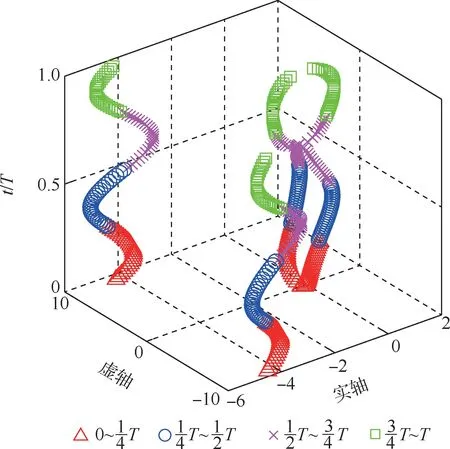
圖6 F 的特征值變化Fig.6 Eigenvalues of F

可以看到,機(jī)翼的周期性撲動使得線性時變周期系統(tǒng)F中的模態(tài)極點(diǎn)周期性變化。 其中,2 個離虛軸較遠(yuǎn)的短周期模態(tài)極點(diǎn)的周期性變化表明系統(tǒng)短周期的阻尼比和自振頻率周期性變化,短周期平均阻尼比為0.399 9,短周期平均自振頻率為10.371 2 rad/s。 雖然短周期模態(tài)周期性變化,但其是穩(wěn)定的,這是合理地選擇平尾尾容比和平尾力臂等參數(shù)的結(jié)果。 此外還可以看到,2 個離虛軸較近的特征值在復(fù)平面的左右兩邊來回運(yùn)動,這意味著該系統(tǒng)存在靜不穩(wěn)定的模態(tài)。因此,撲翼機(jī)是否周期穩(wěn)定并不能由F直接確定,必須通過Floquet 動穩(wěn)定性分析確定。

1.4 控制輸入各通道操縱效率分析

本節(jié)在基準(zhǔn)飛行狀態(tài)下,以估算得到的操縱導(dǎo)數(shù)系數(shù)為原始數(shù)據(jù),用G中各元素的表達(dá)式,計(jì)算得到仿鴿撲翼機(jī)的各輸入通道的操縱效能,并對其進(jìn)行分析,以明確各輸入的操縱作用,從而為控制器的設(shè)計(jì)提供依據(jù)。

在2 個撲動周期內(nèi),撲翼機(jī)升降舵偏轉(zhuǎn)的操縱效能、機(jī)翼撲動角振幅的操縱效能及機(jī)翼扭轉(zhuǎn)角振幅的操縱效能如圖7 所示,其中T為周期,1T=0.1 s。

如圖7 所示,升降舵的偏轉(zhuǎn)主要使q的平均值發(fā)生變化,從而改變撲翼機(jī)的俯仰姿態(tài)和平衡撲翼機(jī)的俯仰力矩。

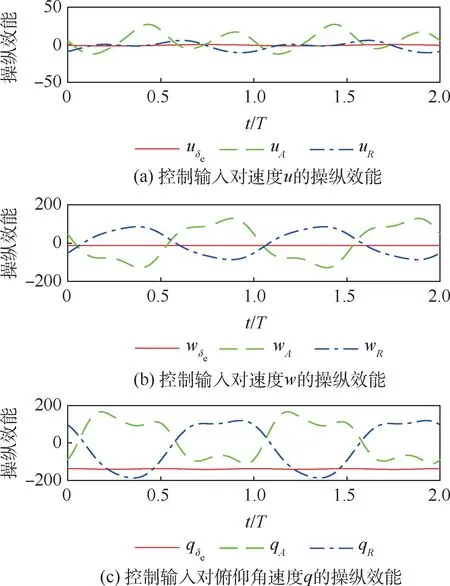
圖7 控制輸入的操縱效能Fig.7 Control efficiency of inputs

此外,uA、wA及qA隨機(jī)翼的周期撲動而周期變化且其振幅都特別大,這是因?yàn)閾湟頇C(jī)的升力和推力主要是由機(jī)翼的撲動產(chǎn)生,而撲翼的升力和推力中心線不是一直通過撲翼機(jī)重心,而是隨著機(jī)翼的撲動不斷地變化。 在一個周期內(nèi),uA、wA和qA的平均值分別為5. 066 6 m/(s·rad)、0.676 7 m/(s·rad)和19.752 4 s-1。 可以看到,A增大可以使u增大,這與增大A來增大撲翼機(jī)推力的操縱機(jī)制相符合。 另外,由于qA的平均值較大且振幅較大,A的改變必將引起q的改變。因此,對撲翼機(jī)縱向俯仰姿態(tài)的控制需要升降舵和機(jī)翼撲動角振幅共同配合來完成。

由圖7 可知,R增大對u、w和q的平均值影響很小,且對q的平均值影響可以通過升降舵來調(diào)節(jié)。 另外,在一個撲動周期內(nèi),wR的振動方向與wA相反,qR的振動方向與qA相反,uR的最大值相對于uA較小。 因此,在增大A的同時調(diào)節(jié)R的大小可以減緩撲翼機(jī)飛行時q和θ的振動及法向過載nz的振動。

2 基于Floquet 理論的線性時變周期系統(tǒng)的動穩(wěn)定性分析

考慮到Floquet 理論具有較高的準(zhǔn)確性[26],本節(jié)采用該理論對機(jī)翼質(zhì)量占比為6.67% 的仿鴿撲翼機(jī)線性時變周期系統(tǒng)進(jìn)行動穩(wěn)定性分析。

當(dāng)存在小擾動量時,線性時變周期系統(tǒng)的微分方程為

式中:F(t)∈Rn×n且F(t+T) =F(t),x(t)∈Rn×1。式(7)的基解矩陣為非奇異矩陣ψ(t)∈Rn×n。

存在非奇異常值矩陣C∈Rn×n滿足:

矩陣C的特征值ρ1,ρ2,…,ρn即為式(7)的特征乘子。 根據(jù)Floquet 理論,可以獲得以下關(guān)系:

式中:k∈N。 此時擾動狀態(tài)量xj隨時間的變化與矩陣C的特征值大小有關(guān)。 當(dāng)矩陣C所有的特征值都在單位圓內(nèi)時,擾動量將隨時間的增加而逐漸消失,系統(tǒng)穩(wěn)定;否則系統(tǒng)不穩(wěn)定。

在基準(zhǔn)飛行狀態(tài)下,C的特征值為

矩陣C特征值模的最大值大于1,在單位圓外,系統(tǒng)動不穩(wěn)定。

3 仿真分析

3.1 開環(huán)仿真結(jié)果

在基準(zhǔn)飛行狀態(tài)下,給升降舵一個脈沖信號,仿鴿撲翼機(jī)的開環(huán)響應(yīng)如圖8 所示。

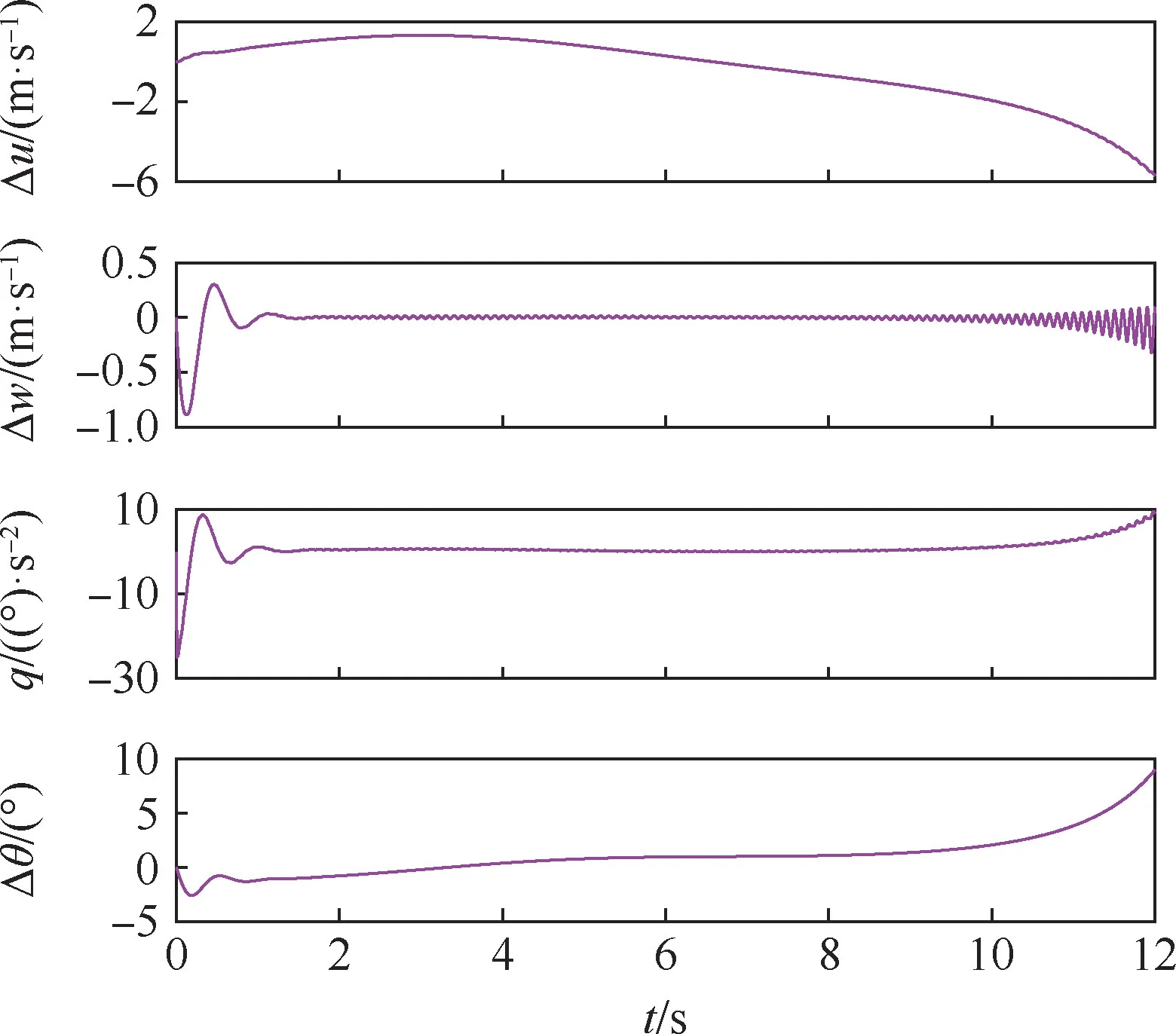
圖8 升降舵脈沖信號下的開環(huán)仿真響應(yīng)Fig.8 Open-loop simulation response under elevator pulse signal

如圖8 所示,在給升降舵一個脈沖激勵信號后,在短時間范圍內(nèi),w和q較快地穩(wěn)定下來,仿鴿撲翼機(jī)具有穩(wěn)定的短周期模態(tài),與1.3.3節(jié)分析結(jié)果一致。 在長時間范圍內(nèi),u發(fā)散,而其他3 個狀態(tài)量先是穩(wěn)定在一個值上,最終隨著u的發(fā)散而發(fā)散,這與第2 節(jié)的分析結(jié)果一致。

3.2 經(jīng)典控制器設(shè)計(jì)

利用串級PID 經(jīng)典控制算法設(shè)計(jì)了圖9 所示的縱向軌跡跟蹤控制器,以Δδe、ΔA和ΔR作為控制輸入,高度h和u作為輸出。 此外,針對操縱輸入的冗余問題,考慮到有效集方法具有計(jì)算方便、步驟簡單、實(shí)時性好等優(yōu)點(diǎn),采用有效集方法[27],進(jìn)行控制分配器的設(shè)計(jì),實(shí)現(xiàn)了升降舵和機(jī)翼扭轉(zhuǎn)角振幅對俯仰姿態(tài)角回路的聯(lián)合控制,其中ucmd為需要跟蹤的u的指令信號,hcmd為需要跟蹤的h指令信號,符號上方“ -”表示負(fù)反饋。

圖9 縱向雙通道閉環(huán)控制器結(jié)構(gòu)Fig.9 Structure of longitudinal dual channel closed-loop controller

3.3 閉環(huán)仿真分析

在基準(zhǔn)飛行狀態(tài)下,給定一組周期為40 s、振幅為5 m 的正弦高度指令信號,對閉環(huán)系統(tǒng)進(jìn)行仿真。 為了驗(yàn)證將ΔR作為控制輸入的效果,將采用帶控制分配的Δδe、ΔA和ΔR的三輸入閉環(huán)仿真結(jié)果與只采用Δδe和ΔA二輸入的閉環(huán)仿真結(jié)果進(jìn)行對比。 最終的狀態(tài)量響應(yīng)和操縱響應(yīng)分別如圖10 和圖11 所示。

由圖11(a)可以看出,撲翼機(jī)要跟蹤h指令時,首先要偏轉(zhuǎn)Δδe來改變q,從而改變θ來實(shí)現(xiàn)h的變化,同時,由圖11(b)可以看出,為了避免h變化引發(fā)的u變化,要改變ΔA來改變機(jī)翼撲動的速度。 此外,由圖10(a)、圖11(a) 和圖11(b)可以看到,撲翼機(jī)并不是完全依靠Δδe來改變俯仰姿態(tài),如在30 ～40 s 撲翼機(jī)上升時,Δδe處于上偏狀態(tài),這是因?yàn)榇藭rA增大,其在產(chǎn)生推力的同時也會產(chǎn)生俯仰力矩從而對q產(chǎn)生影響,這一點(diǎn)也與圖7 中qA的平均值19.752 4 s-1相符合。因此,對撲翼機(jī)俯仰姿態(tài)的操控是通過Δδe和ΔA的變化共同來完成。

圖11 閉環(huán)系統(tǒng)操縱響應(yīng)Fig.11 Control response of closed-loop system

此外,從圖10(c) ～圖10(f)可以看出三輸入模型的θ、q的振幅及˙q和nz的最大絕對值要明顯小于二輸入模型。 其原因在于:引入ΔR控制輸入后,通過機(jī)翼在撲動過程中的扭轉(zhuǎn)實(shí)時地調(diào)整機(jī)翼迎角,從而達(dá)到調(diào)整機(jī)翼產(chǎn)生的升力、阻力的大小和方向的目的,進(jìn)而使得在撲動過程中全機(jī)的CL和Cm的振幅更小,最終達(dá)到減緩θ、q的振幅及˙q和nz的最大絕對值的效果。

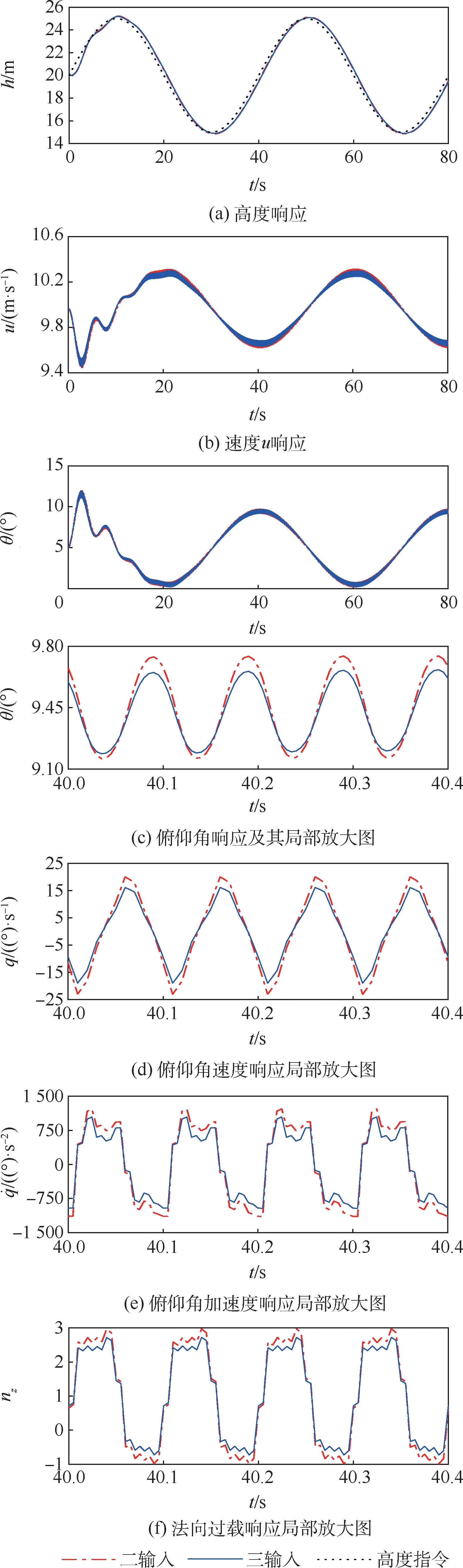
圖10 閉環(huán)狀態(tài)量響應(yīng)Fig.10 States response of closed-loop system

為對引入ΔR后的控制效果進(jìn)行更有效評價(jià),探索了評價(jià)指標(biāo)的構(gòu)建問題。 撲翼機(jī)飛行時的實(shí)際情況表明,θ振動過大會對空中投彈、偵查拍攝等任務(wù)造成不利影響,˙q和nz過大會使機(jī)體結(jié)構(gòu)承受過大的彎矩和慣性力,從而造成結(jié)構(gòu)疲勞。 因此,為了更清晰地表達(dá)減緩效果,提出式(10)所示的狀態(tài)平緩度指標(biāo):

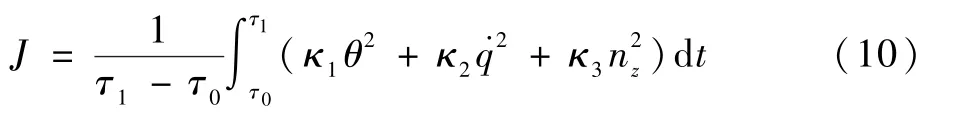
式中:κ1、κ2、κ3為歸一化系數(shù),取值分別為0.373 4、4.152 5 ×10-5、9.809 7;nz為法向過載。 仿真結(jié)果顯示,二輸入模型的狀態(tài)平緩度指標(biāo)為100.501 9,而三輸入模型為83.450 7,減緩了17.05。

4 結(jié) 論

1) 鴿子飛行時常采用變頻率和振幅模式來調(diào)控翅膀撲動、扭轉(zhuǎn)以達(dá)到高效飛行的目的。 研究發(fā)現(xiàn),定周期等振幅撲動翅膀條件下,僅靠尾巴偏轉(zhuǎn)不能既實(shí)現(xiàn)高度的控制又實(shí)現(xiàn)速度的保持和控制,因此,需要引入機(jī)翼撲動角振幅作為控制輸入來實(shí)現(xiàn)速度的保持,同時也有必要引入機(jī)翼扭轉(zhuǎn)角振幅作為控制輸入以進(jìn)一步提升軌跡跟蹤飛行的平穩(wěn)性和高效性。

2) 基于Floquet 理論對仿鴿撲翼機(jī)線性時變周期系統(tǒng)模型展開了動穩(wěn)定性分析,與開環(huán)時域仿真結(jié)果一致,表明了仿鴿撲翼機(jī)具有緩慢發(fā)散模態(tài),從而指明了設(shè)計(jì)增穩(wěn)和控制器的必要性。

3) 閉環(huán)仿真結(jié)果表明機(jī)翼扭轉(zhuǎn)角振幅這一輸入量的引入能顯著提升軌跡跟蹤過程的平滑性,使?fàn)顟B(tài)平緩度指標(biāo)降低了17.05,驗(yàn)證了所建模型的有效性及模型輸入維度增加帶來的模型適應(yīng)性。