顧及似大地水準面趨勢變化的高程異常擬合方法
趙保成 李國忠 徐 堅 徐 健 肖 瀟
(1. 長江科學院 空間信息技術應用研究所, 湖北 武漢 430010; 2. 武漢市智慧流域工程技術研究中心, 湖北 武漢 430010)
0 引言
2020年北斗3號全球組網成功,國際上基本形成了以美國全球定位系統(global positioning system,GPS)、俄羅斯格洛納斯、歐盟伽利略、中國北斗為主的四大全球衛星導航定位系統。伴隨著各星座系統導航衛星數目的增加以及迭代更新,全球導航定位系統(global navigation satellite system,GNSS)在各行各業的應用也將越來越廣泛,尤其對于測繪地理信息行業。GNSS測量具備全天時、全天候、累積誤差小、測站不受通視條件影響的優點,它的出現極大提升了測繪作業效率[1-3]。但是GNSS接收機直接獲取的測點高程信息是基于參考橢球面的大地高,而在實際工程應用中,我國使用的卻是基于似大地水準面的正常高,在不考慮垂線偏差影響的情況下,二者之間存在一個非固定差值即高程異常,因此,如何求取測點高程異常值成為GNSS高程數據成果直接應用于實際工程中需首要解決的關鍵問題。
針對上述關鍵問題,眾多行業學者做出了諸多的嘗試。文獻[4]利用基于穩健估計的總體最小二乘算法較好地解決了高程異常曲面擬合過程中已知點平面坐標與高程異常值中均含有誤差的問題;文獻[5]提出了一種基于多面函數和移動曲面法的綜合高程異常擬合模型,在一定程度上提高了高程異常擬合精度;文獻[6]將多種常見高程異常曲面擬合模型進行加權組合,對不同地形的適應性進行了分析;文獻[7]利用全球超高階地球重力場模型(Earth gravitationational model 2008,EGM2008)去除高程異常中的長波項,進而使用加權組合模型對高程異常的剩余項擬合,擬合效率得到了一定的提升;文獻[8]提出了蟻群—遺傳算法結合多面函數擬合的改進曲面擬合方法,在很大程度上提高了擬合模型的精度;文獻[9]基于二次曲面和EGM2008全球重力場模型,構建了多種移去—恢復型函數擬合模型,探究了各種模型的適用性;文獻[10]利用礦區水準觀測數據及重力場模型,綜合物理和幾何方法建立了礦區似大地水準面模型;文獻[11]構建了二次曲面—徑向基函數(radial basis function,RBF)神經網絡組合的GPS高程轉換模型,提高了單一模型的擬合精度。
綜上所述,現有的高程異常擬合研究多是從擬合函數模型角度自身出發,或是模型的改進,或是多種模型的加權組合,缺少了對參與高程異常曲面擬合的特征點的選取方法的研究,特征點若選取不當,將導致擬合曲面關鍵信息丟失,影響最終的擬合效果。
本文在總結了多位行業學者研究成果的基礎上,提出了一種顧及似大地水準面趨勢變化的高程異常擬合方法,首先利用SGG-UGM-2全球重力場模型預先獲取測區似大地水準面趨勢面特征點,后對特征點進行GNSS水準聯測,最后結合移去恢復法及二次多項式曲面進行高程異常擬合。經過實例驗證,本文提出的高程異常擬合方法,參與高程異常曲面擬合的特征點選取更加合理,關鍵信息損失少,擬合精度能夠達到厘米級,完全滿足絕大多數大比例尺地形圖測量要求。
1 高程系統
我國常用的高程系統有3種,大地高、正高和正常高。大地高H為測點沿法線至參考橢球面的距離,可由GNSS接收機測得;正高h為測點沿鉛垂線至大地水準面的距離,此值為理論值,一般不可直接測得;正常高hr為測點沿鉛垂線至似大地水準面的距離,一般通過水準測量方法確定[12]。三者的幾何關系如圖1所示,數學關系見式(1)與式(2)。我國法定使用的1985國家高程基準使用的高程系統即是正常高系統。式(1)中ζ表示高程異常,式(2)中N表示大地水準面差距。

圖1 高程系統關系圖
2 原理與方法
2.1 利用SGG-UGM-2全球重力場模型求解高程異常中長波項
SGG-UGM-2全球重力場模型是由我國梁偉等學者于2020年采用球諧分析方法構建并發布的一個最新的2 190階2 159次全球重力場模型,模型分辨率為5′,構建此模型使用的數據包括全球衛星重力觀測數據、衛星測高數據和EGM2008全球重力場模型的重力異常數據[13],在我國,此模型精度優于其他全球重力場模型(如SGG-UGM-1、EGM2008等)。以SGG-UGM-2全球重力場模型為基礎,利用Bruns公式[14]求解地球上任意點的高程異常中長波項ζGM,公式如下:
(3)

2.2 二次多項式曲面擬合
曲面擬合常用的方法有二次多項式曲面擬合、多面函數法、曲面樣條函數法、移動曲面法等。在實際工程應用中,為方便計算,大多采用二次多項式曲面函數擬合高程異常短波項,其數學表達如式(4)所示。
(4)
式中,ζ短波為特征點的高程異常短波項;(xi,yi)為特征點在某參考系統內的平面直角坐標;(a0,a1,a2,a3,a4,a5)為曲面模型待定系數。
根據列立方程組可知,共有6個未知數,因此為求解模型系數,至少需要列立6個方程。當已知點個數大于6時,其表達如式(5)所示。
(5)
將式(5)變換為誤差方程形式,如式(6)所示,其中,ε為模型的擬合殘差。
(6)
根據最小二乘法原理,令模型擬合殘差平方和最小(i≥6),在此條件下,可以求得二次多項式曲面模型待定系數X,見式(7),其中式(8)中的P為權矩陣。
2.3 方法總體流程
根據物理大地測量學理論,任意測點高程異常可由為中長波項與短波項構成,中長波分量變化較小,趨勢相對平緩,短波分量主要由地形起伏引起,變化相對較大[15-16],其數學關系如式(9)所示。
(9)
移去恢復法是高程異常擬合的經典方法,該方法能夠有效地去除無關變量對擬合最終結果的影響,移去恢復法思想為:首先將高程異常中變化較小的中長波分量移除,然后對短波項進行曲面擬合并通過插值計算出待求點上的短波項,進而在待定點上恢復中長波分量,最終獲取待求點上的高程異常。本文提出的顧及似大地水準面趨勢變化的高程異常擬合方法對經典的移去恢復法做了相應的改進,其具體操作流程如圖2所示。

圖2 移去恢復流程圖
第一步:確定測區范圍并將其格網化,采用SGG-UGM-2全球重力場模型計算測區格網點的高程異常值(真實高程異常中的中長波項),構建基于高程異常中長波項的似大地水準面模型并將其圖形化顯示。
第二步:利用ArcMap軟件中的空間分析模塊對上一步得到的似大地水準面曲面模型進行地形表面分析,計算其高程異常極大值、極小值、坡向、坡度、曲率等參數,合理選擇似大地水準面趨勢變化較大的特征點作為GNSS水準聯測點,通過GNSS水準方法求出特征點的真實高程異常值。
第三步:特征點的真實高程異常值減去第一步中計算得到的中長波分量,剩余高程異常短波項。以特征點的平面坐標作為輸入值,高程異常短波項作為輸出值,構建二次多項式曲面擬合模型,根據模型曲面方程求解特征點覆蓋范圍內的任意待求點的高程異常短波項。
第四步:利用SGG-UGM-2全球重力場模型計算出待求點的中長波分量,再加上擬合步驟中該點高程異常短波項,最終得到待求點的高程異常值。
3 實驗驗證
3.1 實驗區概況
實驗區位于長江中游城市—武漢市,該區域屬于江漢平原,相對高差較小。實驗區沿武漢市某河流岸線布置,長度約70 km,寬度約0.3 km,實驗區具有狹長條形特點。實驗區內均勻地設置有若干等精度GNSS水準聯測點,點位平面按照《全球定位系統(GPS)測量規范》中D級點要求施測,點位高程按照《國家三、四等水準測量規范》中的三等點要求聯測。
3.2 實驗區似大地水準面趨勢分析
由于實驗區呈線狀分布,因此選擇將實驗區內GNSS水準聯測點自河流上游至下游串聯起來,利用式(1)計算GNSS水準聯測點的高程異常值真值,同時利用SGG-UGM-2全球重力場模型計算GNSS水準聯測點高程異常中長波分量,兩者對比結果如圖3所示。 GNSS水準聯測點的高程異常值中的中長波分量與高程異常的真值變化趨勢基本一致,基本反映了實驗區內似大地水準面趨勢變化情況;實驗區內高程異常值均為負值,說明實驗區似大地水準面整體位于橢球面(2000國家大地坐標系橢球)之下,高程異常的最小值為-15.821 m,最大值為-14.254 m,相差1.567 m,沿河流上游至下游,自西向東,高程異常值的絕對值逐漸變小;實驗區河流中上游段高程異常值變化近似呈線性規律,下游段高程異常值變化劇烈,整體呈現非線性變化特征。
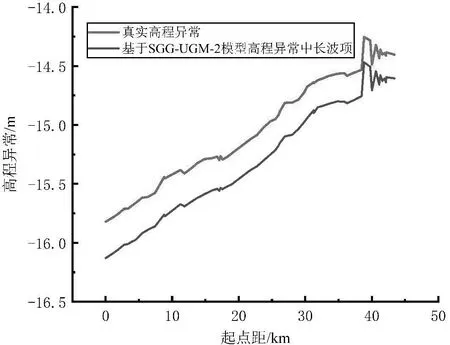
圖3 實驗區似大地水準面趨勢
對于本實驗區的高程異常擬合特征點選取工作:①需保證GNSS水準聯測點覆蓋整個測區;②設置GNSS水準聯測點的點數需確保高程異常擬合曲面方程有解;③根據似大地水準面的地形分析結果,GNSS水準聯測點需在似大地水準面變化大的區域(實驗區下游區)盡量多選點。
3.3 實驗方案設計
為驗證本文提出的高程異常擬合方法的優越性,采用二次多項式曲面擬合法、移去恢復型二次多項式曲面擬合法、顧及似大地水準面趨勢變化的二次多項式曲面擬合法、顧及似大地水準面趨勢變化的移去恢復型二次多項式曲面擬合法4種擬合方案進行高程異常擬合效果對比實驗,將4種實驗方案分別編號為方案1#、方案2#、方案3#、方案4#,如表1所示。

表1 擬合實驗方案表
為減少無關變量對實驗對比結果的影響,4種方案選擇GNSS水準聯測點數量均為8個(最少點數為6),檢核點均為6個,特征點采用黑色圓形表示,檢核點采用三角形表示,各方案的點位選擇空間分布如圖4所示。

(a)方案1#選點方案

(b)方案2#選點方案

(c)方案3#選點方案
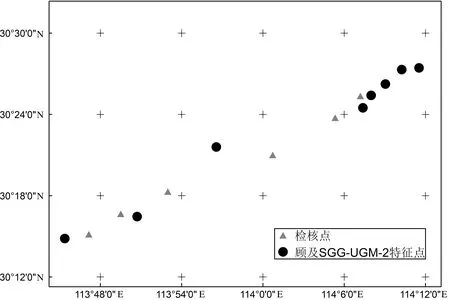
(d)方案4#選點方案圖4 各實驗選點方案
3.4 精度評定
中誤差對一組測量值中的異常值非常敏感,能較好地反映測量結果波動大小,因此本次實驗使用中誤差評定高程異常擬合精度,計算中誤差的表達見式(10)。
(10)
其中,mζ為高程異常擬合中誤差;Δ為在檢核點上曲面擬合模型插值計算的高程異常值與GNSS水準計算得出的高程異常值(真值)的差值;n為檢核點的個數。
3.5 實驗對比分析
對比4種方案的擬合效果,由圖5和表2的結果可得:

圖5 擬合殘差圖

表2 精度評定表 單位:m
(1)不考慮似大地水準面趨勢變化選擇擬合特征點且不使用移動恢復法的方案1#的高程異常擬合效果最差,最大殘差值為0.033 m,最小殘差值為0.012 m,中誤差為±0.025 m;選擇似大地水準面趨勢面特征點參與曲面擬合且使用移去恢復法的方案4#擬合效果最好,最大殘差值為0.027 m,最小殘差值為0.000 m,中誤差為±0.014 m。
(2)對比方案1#與方案3#,二者均未采用移去恢復法,擬合中誤差均為±0.025 m,總體擬合效果相當;方案3#考慮了似大地水準面趨勢變化,相比方案1#的擬合殘差的極大值和極小值都小,在未采用移去恢復法的情況下,考慮似大地水準面趨勢變化有助于提高高程異常擬合精度,但是總體擬合效果并不明顯。
(3)對比方案2#與方案4#,二者均采用了移去恢復法,方案4#考慮了似大地水準面趨勢變化,其擬合中誤差為±0.014 m,方案2#擬合中誤差為±0.017 m,方案4#比方案2#總體擬合精度提升了17.65%。因此,在采用移去恢復法情況下,考慮似大地水準面趨勢變化的選點方案能夠顯著地提升高程異常擬合精度。
(4)由方案1#與方案2#、方案3#與方案4#實驗結果對比表明:移去恢復法能夠有效地提升高程異常曲面擬合精度,其中方案2#比方案1#擬合精度提升32.00%,方案4#比方案3#擬合精度提升44.00%。
4 結束語
基于SGG-UGM-2全球重力場模型,結合移去恢復擬合法,本文提出了一種顧及似大地水準面趨勢變化的高程異常擬合方法。在對陌生測區無任何高程先驗知識的情況下,此方法能夠相對準確地判斷出測區高程異常曲面擬合中關鍵已知點信息,從而減小曲面擬合過程中的精度損失。通過實例驗證,本文提出的高程異常曲面擬合方法最大殘差值為0.027 m,最小殘差值為0.000 m,中誤差為±0.014 m,其完全能夠使實驗區的GNSS高程測量替代四等水準方法。

