多尺度點云濾波去噪方法
劉翔宇 宋 羽
(1. 山東科技大學 測繪與空間信息學院, 山東 青島 266590; 2. 濟南市勘察測繪研究院, 山東 濟南 250013)
0 引言
由三維激光掃描儀直接獲得的點云數據在實際應用之前往往需要進行一系列的優化處理,低質量的點云數據會對其應用、分析造成巨大的影響[1]。在點云濾波去噪領域,中值濾波與高斯濾波最早被應用于噪聲的濾除[2],其中,中值濾波通過對當前采樣點與其鄰域點進行均值計算,將計算出來的均值點作為當前點的位置,原理相對簡單,但易產生新的噪聲且濾波效果不佳。由于改變了點云位置,無法保持點云細節特征;高斯濾波通過對點云及其鄰域點距離進行加權處理,按距離大小分配權重,根據其大小判斷噪聲,其方法在細節特征上有所保留,但濾波效果不佳,特別是密集型噪聲難以去除。Yagou等[3]采用網格濾波的方式,對網格法線應用均值濾波和中值濾波,然后更新網格頂點位置,以使網格適應修改后的法線,該方法雖然對噪聲有明顯的濾除效果,但易發生形變。Desbrun等[4]針對拉普拉斯濾波算法的弊端做相關研究,提出了基于平均曲率流的方法,在濾波過程中使頂點的移動沿著法方向進行,有效地避免了頂點漂移。但是這種方法會導致尖銳點部分點云特征無法得到很好地保持。為避免上述情況的發生,Clarenz等[5]通過求解離散的各向異性擴散方程,實現了點云濾波。梁新合等[6]結合點云實際特征,利用三邊濾波算法做到了研究區域自適應的濾波降噪。葉珉呂等[7]將最小二乘擬合的點云模型與點云進行距離探測,通過設定閾值判定噪聲,但局限性較大,且難以保持精度。Fleishman等[8]提出了一種快速的、基于二維雙邊濾波圖像去噪原理的各向異性三維點云濾波去噪算法,通過使用局部鄰域在法線方向過濾網格頂點的方式,對傳統濾波算法邊緣特征難以保留的缺陷進行了改進,但復雜度較高,對于復雜噪聲的處理情況并不理想;王麗輝等[9]將聚類算法與雙邊濾波算法相結合,提出了通過模糊C均值(FCM)聚類算法實現大尺度噪聲去除并通過雙邊濾波方法進行精細化去噪的點云濾波方法;曹爽等[10]通過對點云網格化,采用基于特征選擇的方式將點云分為特征點與非特征點,采用不同的濾波參數進行去噪,雖然可以進一步保證點云邊緣特征,但操作復雜,魯棒性不強;袁華、李明磊[11-12]等先后在雙邊濾波算法的基礎上進行改進,并在自己的研究領域取得了不錯的成果;韓浩宇等[13]給出了一個結合雙張量投票和多尺度法矢量統計的點云濾波算法,該方法在有效剔除噪聲點的同時保留了點云模型的尖銳特征。
針對上述問題,本文在結合現有去噪算法的基礎上,研究一種多尺度點云去噪算法,期望解決傳統點云濾波算法會丟失物體細節特征的問題,為后續點云配準與點云重建提供基礎。
1 理論方法
1.1 基于統計分析的大尺度遠離群點去噪方法
大尺度噪聲主要指位于主體點云附近的離散稀疏點云或距離較遠的小型密集點云,從點云整體看,主體點云多而集中,噪聲點云小而分散[14],本文基于統計分析的去噪方法就是利用主體點云點與鄰域點間的距離小、離散點云到鄰域點間的距離大的特點來實現對于離散點的判別。即通過計算采樣點到鄰域點集的距離進行統計分析進而進行離群點的判別,去除無用噪聲。
基于統計分析的點云去噪方法的具體流程如下:
(1)設定采樣點集P={pi∈R3|i=1,2,…,n},其中,對任一點pi的鄰域內有k個臨近點,即其K鄰域,記為Pij={pi1,pi2,…|j=1,2,…,k}。
(2)設定K鄰域的大小,計算采樣點pi到其K鄰域的平均距離ui,如式(1)所示。
(1)
(3)重復計算所有采樣點,得到每個采樣點到設定K鄰域的平均距離,通過計算得到全局平均距離un與標準差σ,如式(2)與式(3)所示。
(4)設定標準差倍數閾值std,得到距離閾值un±σ·std,對每一個采樣點pi到K鄰域的距離ui與全局平均距離un進行判定,對ui>un的點進行去除,反之保留為主體點云。
1.2 基于小尺度的近離群點去噪方法
本文基于引導濾波原理將其從二維像素擴展到三維點云,實現點云的近離群點去噪。兩種方式都具備一致的思想:在梯度變化較大的地方實現保留,盡量不平滑;而在梯度比較小的地方,進行平滑濾波。在三維空間中,根據引導濾波的基于局部特征的原理,將二維圖像中通過梯度變化識別邊緣區域改進為通過判定點云鄰域協方差矩陣大小進行判定邊緣區域,具體原理如下:
(1)通過KD-tree數據結構來構造點云,通過K鄰近分類(K-nearest neighbors,KNN)確定其鄰域N(pi)。
(4)
式中,|N(pi)|為N(pi)的基數。
(4)由協方差矩陣∑i與參數,計算線性因子根據協方差矩陣反應點云形態變化程度:當處于平坦區域時, ∑i?,則ai≈0,做均值濾波,處于邊緣區域時,∑i?,ai≈1,bi≈0,基本保留點云邊緣特征。最終實現自適應濾除平緩區域點云,保留點云邊緣特征。
(5)通過對每個點計算與其鄰域進行線性變換求取pi在自身鄰域N(pi)中的濾波點,進行局部濾波去噪。
1.3 多尺度點云濾波方法
通過將離群點劃分為遠距離的大尺度噪聲與近距離的小尺度噪聲,利用統計分析原理高效的特點,初步、快速去除較遠位置的點云,降低其干擾,進而進行局部濾波,將圖像引導濾波算法拓展到三維點云中,去除近離群點點云,通過點云及其鄰域的協方差矩陣大小,反應點云局部形態變化,最大限度上降低濾波對于原始點云數據的影響,保證后續點云應用的精度。具體流程如圖1所示。
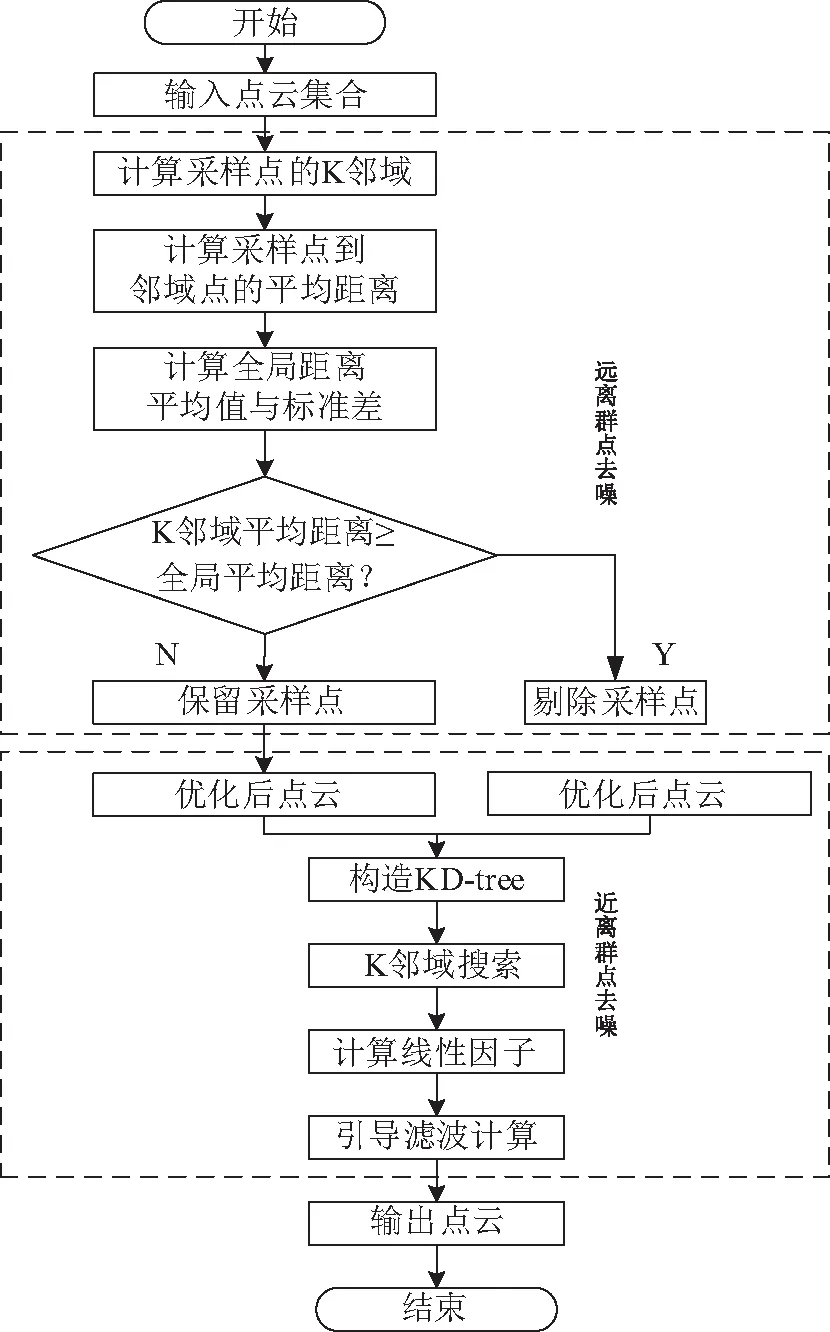
圖1 算法流程
2 實驗驗證
為驗證本文算法,選取斯坦福大學的標準Chair點云模型數據和某實測土坡數據,并對標準點云數據進行加噪處理,如圖2所示,在點云附近0~5 mm、50~55 mm以及更遠區域分別添加一定量的噪聲,模擬遠近不同距離的離群點。

(a)加噪Chair數據

(b)坡體整體數據圖2 實驗數據
針對兩種點云數據分別使用統計濾波、半徑濾波。雙邊濾波和本文算算法進行去噪處理,具體如圖3、圖4所示。
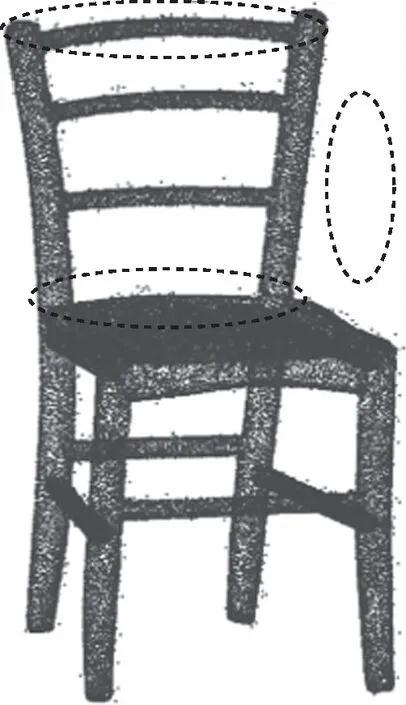
(a)統計濾波

(b)半徑濾波
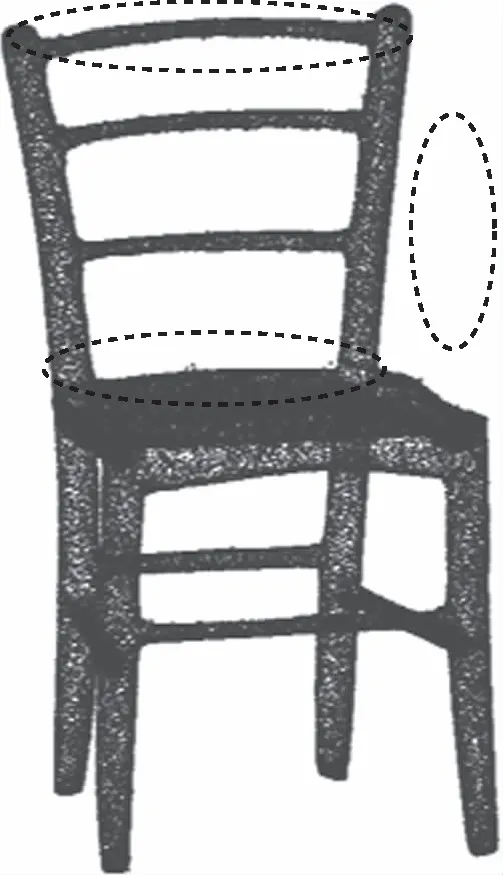
(c)雙邊濾波

(d)本文算法圖3 Chair點云濾波效果對比

(a)統計濾波

(b)半徑濾波

(c)雙邊濾波
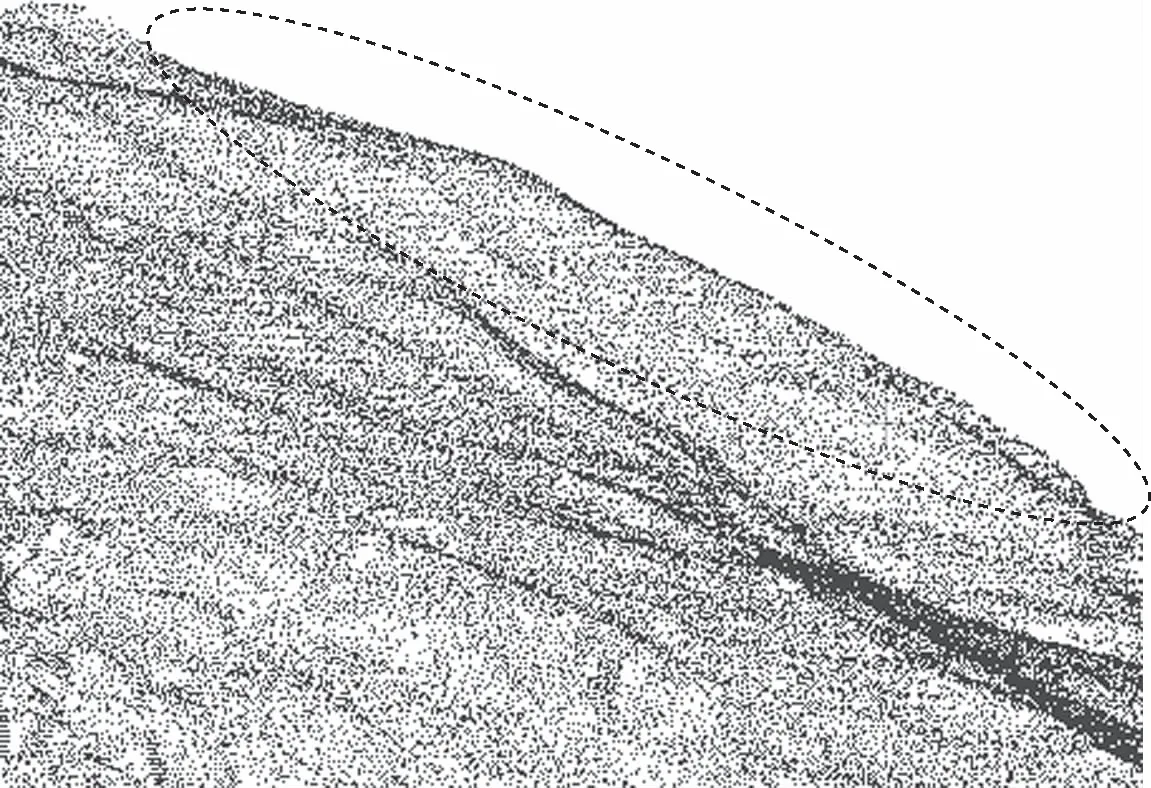
(d)本文算法圖4 坡體點云濾波效果對比
從圖3(a)和圖4(a)可以看出統計濾波對較遠位置的離群點可以有效地去除,但是對于分布在主體點云附近的近距離離群點去除效果較差。分析圖3、圖4中的(b)(c),采用半徑濾波根據檢索半徑和判定半徑區域內臨近點的個數是否符合閾值來進行離群點的判定,雖然可以有效地去除噪聲,但由于近離群點距離主體過近,會產生錯誤的判斷,造成主體點云缺失,嚴重影響精度。雙邊濾波雖然在近離群點處效果較好,也能夠一定程度上保持邊緣特征,但存在局部區域過渡平滑、精度喪失的現象。通過分析圖3、圖4中的(d)可以看出本文算法可以有效去除近離群點噪聲,同時最大限度上完整保留點云的邊緣信息,降低噪聲對精度的影響。
3 結束語
本文針對在使用傳統濾波方法進行去噪時,不能兼顧濾波效果與保留細節特征,會造成精度丟失的問題。采用基于統計分析的點云去噪方法去除大尺度噪聲,結合圖像引導濾波原理去除小尺度噪聲。最后選用標準Chair數據和實測某土坡數據進行實驗驗證,實驗結果表明本文算法在保留特征、去除遠近離群點上效果較為明顯,對實測點云數據具備較好的適應性。

