基于城軌電客車軸箱振動加速度的軌道短波不平順識別方法

王凱峰，李明航，李玉路，吳宗臻，王小鎖

（1.石家莊市軌道交通集團有限責任公司，河北石家莊 050000；2.中國鐵道科學研究院集團有限公司城市軌道交通中心，北京 100081）

1 研究背景

軌道不平順是軌道狀態的重要評價指標，按照波長可以分為長波、中波及短波不平順，是影響列車運行的安全性以及旅客舒適性的關鍵因素。軌道幾何檢測系統通常能識別2～150 m 內的中長波不平順，但較難識別判斷波長1 m 以下的短波不平順。軌道短波不平順往往由鋼軌接頭不平順、焊縫、鋼軌表面波浪磨耗等因素造成。列車的長期運行會導致相應部件疲勞損傷，軌道服役狀態惡化，甚至會引發局部軌道結構破壞進而危及行車安全，危害較大。因此，鋼軌短波不平順的特征識別與治理一直是城市軌道交通領域關注的重點課題。圖1為部分典型短波不平順造成軌道服役狀態惡化狀態。

圖1 短波不平順造成軌道服役狀態惡化

近年來，智能化運維已逐漸成為城市軌道交通（以下簡稱“城軌”）的發展趨勢，《中國城市軌道交通智慧城軌發展綱要》明確提出，2025年城軌智能車輛占有率要達到95%以上，并且要實現車載各系統數據的采集、預警、遠程監視及診斷分析，為車輛智能運維系統提供數據支撐，提高列車日常檢修效率，降低列車運維成本。因此，有必要研究通過城軌電客車進行數據采集，精準識別短波不平順關鍵特征，科學合理地評判鋼軌狀態，并根據狀態情況進行維修。

由于軌道短波不平順會導致列車運行時軸箱產生劇烈的高頻振動，因此許多學者探索采用軸箱振動加速度來識別軌道短波不平順的技術方法。劉金朝等提出采用軌道沖擊指數評判軌道的短波不平順狀態的方法。牛留斌等在文獻[2]基礎上建立輪軌接觸有限元模型，研究了特定軌道條件下鋼軌波磨指數變化規律及其與軌道短波不平順幅值之間的定量關系，給出相應的鋼軌波磨指數限值；通過文獻[4]詳細總結了軸箱振動加速度的常用分析方法。徐曉迪等通過軸箱振動加速度數據獲得了鋼軌波磨典型波長，并基于快速傅里葉變換和頻域積分的方法計算了波磨幅值。

既有研究表明，依據軸箱振動加速度數據計算的鋼軌波磨指數可反映波磨的嚴重程度，但研究的絕大部分是針對速度高且較為均勻的高速鐵路檢測。對于城軌電客車運行速度較低、頻繁加減速等運行特征，既有方法的適用性值得關注且需進行進一步研究。本文基于電客車軸箱振動加速度的實測數據，對文獻[2]提出的波磨指數進行改進，使其能更準確地識別城軌中的短波不平順，并結合時頻分析技術分析得到波磨區段的典型波長。

2 利用軸箱垂向振動加速度評判軌道短波不平順狀態的方法

2.1 波磨指數概念及計算方法

軸箱振動加速度信號具有明顯的隨機性，從能量的統計指標出發，采用軸箱垂向振動加速度的運行有效值（Running RMS）可有效評判軌道的短波不平順狀態。同時，對分析結果的均值做歸一化處理，可有效判別短波不平順的閾值。根據參考文獻[2]，軸箱垂向振動加速度有效值的快速計算方法：

式（1）中，S為軸箱垂向加速度有效值，m/s2；N為軸箱垂向加速度采樣點數；i為軸箱垂向振動加速度的樣本數，i= 1，2，…，N；a為帶通濾波（10～1 000 Hz）后的軸箱垂向加速度，m/s2；K為移動計算有效值的窗長。

波磨指數為軸箱垂向振動加速度移動有效值與其平均值的比值，即：

式（2）中，TⅡ為波磨指數；Sr為測點r處軸箱垂向振動加速度的移動有效值，m/s2；為軸箱垂向振動加速度移動有效值的平均值，m/s2。

2.2 改進后的波磨指數計算方法

車輛通過鋼軌波磨區段時，輪軌間產生高頻的激勵振動，激勵頻率f為：

式（3）中，f為激勵頻率，Hz；v為車輛通過速度，mm/s；λ為鋼軌波磨區段軌道不平順的波長，mm。

文獻[2]的計算方法是面向運行速度較為均勻的軌道檢測列車開發的，其速度固定條件下，通過帶通濾波頻段，即可獲得較為穩定的某一特征波長段的振動響應，并由式（3）計算出所關心的頻段。

然而，對于城軌電客車的實際測試條件，列車運行過程中頻繁加減速且運行速度較低，難以采用統一的速度提取振動響應穩定的特征頻率，并計算特征波長；另一方面，通過對短波不平順的分波長統計分析，有利于初步判斷不同測試區段的短波不平順空間分布特征。因此，本文考慮了速度時變特性，將固定頻率的檢測指標改進為分波長控制，在文獻[2]的研究基礎上提出了改進的波磨指數。圖2為改進波磨指數的計算示意圖。

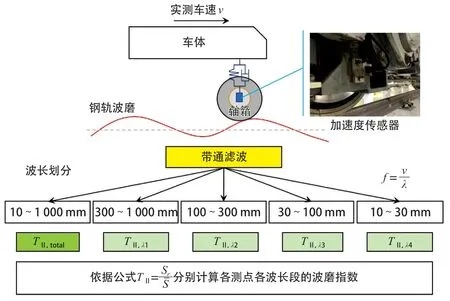
圖2 改進的波磨指數計算示意圖

首先給出2 個定義：將0.01～1 m 波長段對應的波磨指數定義為TⅡ，total；參考BS EN 13231-3 : 2012 規定的分析指標，將短波不平順波長劃分為0.3～1 m，0.1～0.3 m，0.03～0.1 m，0.01～0.03 m，將這4 段波長區間對應的波磨指數分別定義為TⅡ，λ1，TⅡ，λ2，TⅡ，λ3，TⅡ，λ4。

改進后的波磨指數計算過程如下：

（1）劃分測試數據，選取分析窗長為1 s，并設置合適的重疊系數（本文選定為19/20）；

（2）將短波不平順波長劃分為0.3～1 m，0.1～0.3 m，0.03～0.1 m，0.01～0.03 m 4 段，依據不同分析窗的實時的1 s 內平均速度，計算各波長所對應的頻段；

（3）依據上述計算到的頻段，對實測的各測點處軸箱垂向振動加速度進行帶通濾波截取；

（4）計算濾波后各測點處各波段軸箱垂向振動加速度的移動有效值Sr，λi；

（5）計算全部測點處軸箱垂向振動加速度的移動有效值的平均值，即為標定參數 ；

（6）計算各測點的總的波磨指數TⅡ，total及分波長波磨指數TⅡ，λi。

3 計算結果對比分析

3.1 波磨指數分析結果

利用原有的頻率控制方法和本文改進的波長控制方法對城軌電客車的軸箱垂向振動加速度進行分析，以診斷軌道的短波不平順狀態，并對2 種方法的分析效果進行對比。

實測列車通過某城軌區段內軸箱垂向振動加速度原始波形及計算得到的波磨指數如圖3所示。參考波磨指數的計算公式（2），理想狀態下，全分析區段的波磨指數應趨近于1。由圖3可以看出，原有的通過關心頻率（10～1 000 Hz）控制方法計算的波磨指數在勻速階段（35～60 s）能準確的定位鋼軌波磨區段，在變速階段（80～100 s），軸箱振動加速度明顯放大，但傳統波磨指數并未發生顯著的突變。本文提出的改進后的波磨指數更能凸顯該區段的鋼軌粗糙狀態變化。此外，在25～30 s 及108～115 s 范圍內的分析結果顯示，改進的鋼軌波磨指數可有效抑制鋼軌接頭等引起的瞬時振動響應的統計結果。

圖3 波磨指數分析結果對比

圖4給出了分波長波磨指數統計結果。顯然，分波長波磨指數可以更明確地分析波磨區段的顯著波長。35～60 s 內的波磨區段主要為300～1 000 mm、10～100 mm 波長的波磨，100～300 mm 波長的波磨指數在全時段接近1。80～100 s 內的波磨區段特征波長則主要分布在10～100 mm 范圍。10～30 mm 段的波磨指數波動趨勢與30～100 mm 的相似，這是由于鋼軌波磨會激勵起典型波長控制頻率的倍頻響應，該波長段的振動響應是對應20～60 mm 波長引起的。

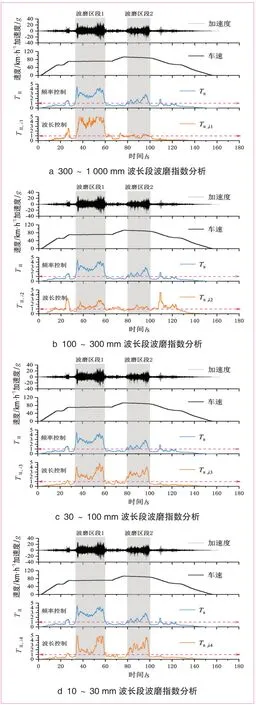
圖4 不同波長段波磨指數分析結果

3.2 特征波長提取

通過改進后的波磨指數可以有效定位發生鋼軌波磨的區段，時頻分析方法則可以提供時間域與頻率域的聯合分布信息。通過時頻分析技術，可將非平穩信號表示為時間和頻率的二維函數，能更加直觀地描述信號頻率隨時間變化的關系。常見的時頻分析方法有短時傅里葉變換（STFT）、小波變換（WT）以及希爾伯特黃變換（HHT）等。

截取35～60 s 及80～100 s 2 個發生鋼軌波磨區段的振動響應進行時頻分析，得到實測振動響應的時頻分布特征，如圖5所示。參考圖5拾取不同時刻的特征頻率，綜合考慮提取得到的特征頻率及實測車速，由式（3）可計算典型波長。

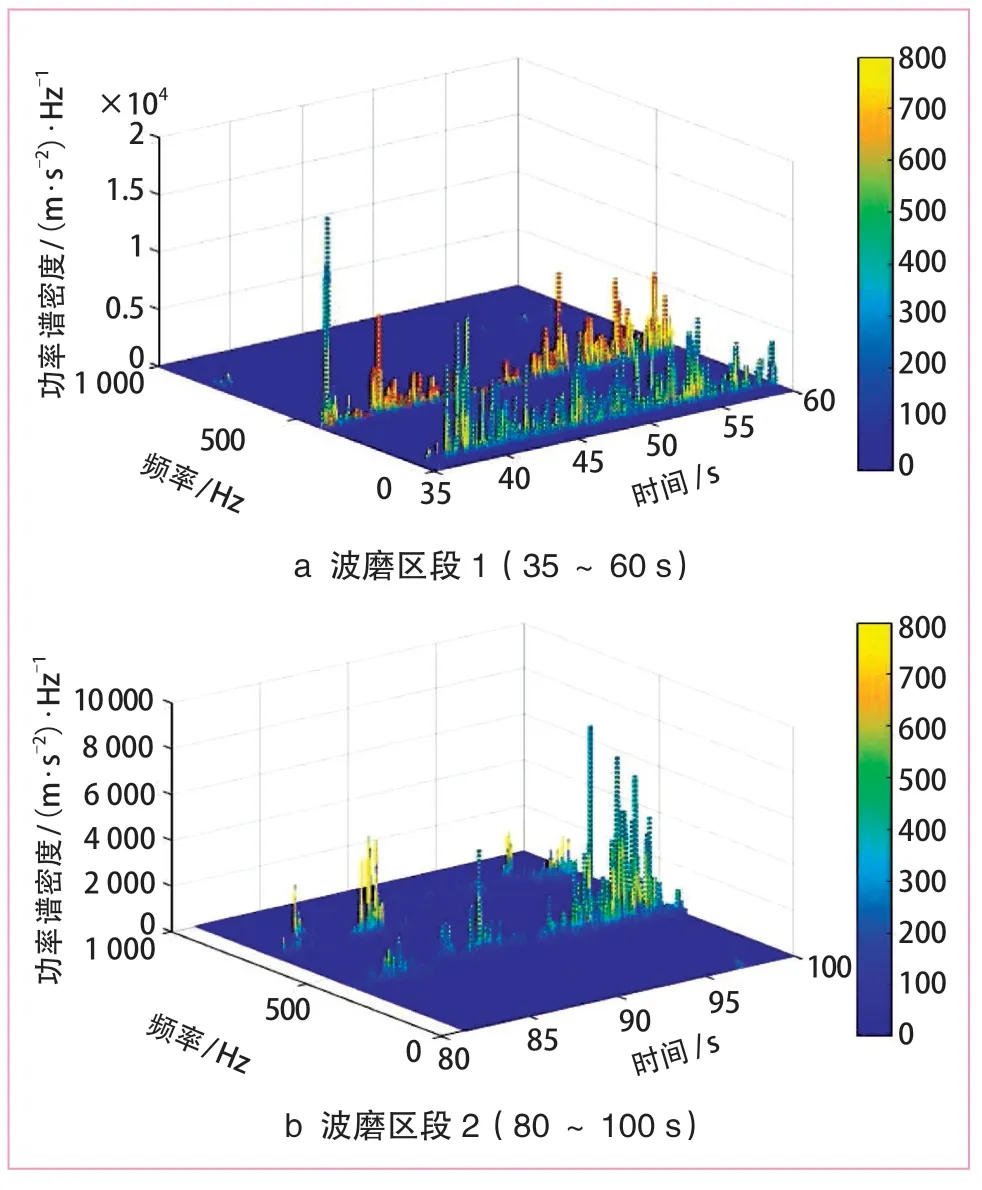
圖5 時頻分析得到的三維譜陣

圖6a 及6b 分別為35～60 s，80～100 s 的區段內特征頻率和典型波長的分析結果。從圖6可以看出，在35～60 s 內有2 個特征頻率為50 Hz 和400 Hz 左右，對應2 個典型波長為370 mm 和50 mm 左右；在80～100 s 區段內特征頻率為400 Hz 左右，對應典型波長為60 mm 左右。

圖7及圖8分別給出了區段2 的鋼軌波磨情況的現場調研結果，其1/3 倍頻程波長中心波長為63 mm，與圖6b 給出的分析結基本一致。因此，本文提出的計算分析方法對城軌電客車頻繁加減速、運行速度較低的特點具有較好的適用性，在有效提取波磨病害發生區段的同時，結合時頻分析技術可準確提取特征波長。

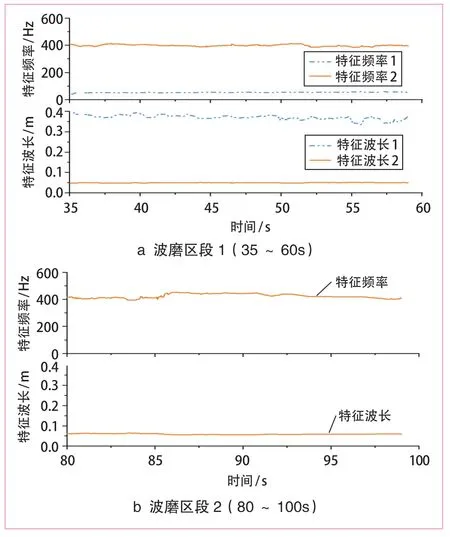
圖6 特征頻率和特征波長拾取結果

圖7 現場鋼軌波磨照片（區段2）

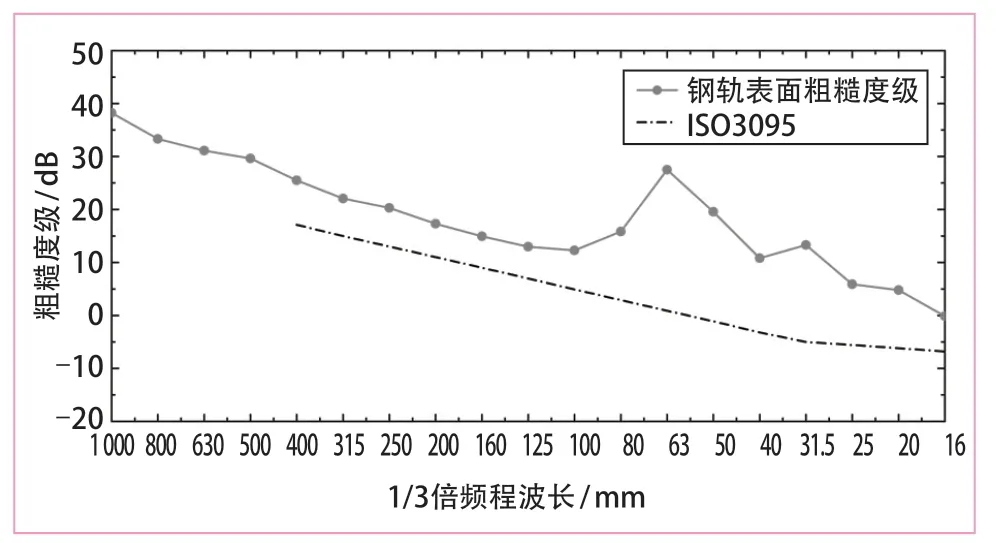
圖8 實測鋼軌表面粗糙度級（區段2）

4 結論

為提升城軌鋼軌波磨病害的檢測效率，本文基于電客車軸箱振動加速度的實測數據，提出了改進后的波磨指數計算方法。該方法能夠反映波磨發生區段的鋼軌粗糙狀態，并且可以有效抑制鋼軌接頭等引起的瞬時沖擊對檢測結果的影響；以分波長段波磨指數作為初步判斷依據，結合時頻分析技術，可準確提取鋼軌波磨的特征波長信息。針對城軌電客車運行速度較低、頻繁啟停的運行特征，本文的方法具備良好的適用性。