基于時空地理加權回歸模型的中國肺結核發病情況及影響因素研究

趙明揚，周乾宇，王榮榮，王宗熹，何雯倩，張文森，張恒榛，田卓旸，吳柯，王碧瑤，孫長青，*

肺結核是由結核分枝桿菌引起的具有強烈傳染性的慢性呼吸系統傳染病，是危害人體健康的重大傳染病之一［1］。肺結核患者在排菌期，即痰菌陽性時具有傳染性，1例未經治療的排菌期活動性肺結核患者1年內可感染15～20名接觸者。2019年全球結核報告顯示，全世界每年約有1 000萬人感染結核病，潛伏性結核感染人數占世界人口總數的1/4左右；中國新發結核病病例833 000例，發病率為58/10萬，位居世界第三，是結核病高負擔國家，肺結核防控形勢依舊嚴峻［2］。

隨著地理信息技術的發展和完善，大量基于空間計量學的空間統計分析方法被提出，地理信息系統和空間統計學在各領域得到廣泛應用。英國學者Fotheringham提出的研究空間關系和空間相關關系的地理加權回歸（geographical weighted regression，GWR）模型可以直觀地探測空間關系的非平穩性［3］，并在多學科領域得到廣泛應用［4-6］。但GWR模型只將數據的空間特性納入模型，而忽略了時間特性對其的影響，在處理某些時間特性和空間特性均突出的數據資料時存在一定局限性。因此，香港大學黃波教授在GWR模型的基礎上提出了時空地理加權回歸（geographically and temporally weighted regression，GTWR）模型［7］。此模型能夠更好地對數據的時空分布及特性進行評估，有效解決了回歸模型的時空非平穩性，一經提出便得到廣泛關注，并在眾多學者的應用過程中不斷完善［8-10］。

近年來，國內外學者對肺結核的時空分布進行大量研究表明，肺結核具有較強的時間特性和空間特性［11-13］。但現有研究更多的是對肺結核發病的影響因素進行獨立的時間或空間回歸分析，研究結果存在局限性，例如使用差分整合滑動平均自回歸模型（autoregressive integrated moving average model，ARIMA）對肺結核數據進行時間序列分析時，忽略了其對應的空間因素的影響［14-15］；在使用空間聚類和地理加權回歸時，肺結核數據所具有的時間特性便無法體現［16］。因此，將時間因素和空間因素同時進行回歸分析，采用GTWR模型對影響肺結核發病的影響因素進行擬合分析是十分必要的。

綜上所述，本文將使用GTWR模型探索中國肺結核分布的時間和空間異質性，并分析肺結核發病情況與氣象和空氣質量因素在時間和空間上的相關關系，為制訂相應結核病防控措施提供科學參考。

1 材料與方法

1.1 數據來源 本研究使用的肺結核發病情況相關數據來源于公共衛生科學數據中心（https://www.phsciencedata.cn/Share/）中的2016—2018年全國分地區（除香港、澳門、臺灣外的31個省份）肺結核分月統計數據，選取的指標為發病率（每10萬人中病例數）。氣象資料數據（包括月平均氣溫、濕度、風速等）來源于天氣后報網（http://www.tianqihoubao.com/）。空氣質量指數數據（包括PM2.5、PM10、SO2、NO2、CO、O3等的月平均濃度）來源于空氣質量指數歷史數據網站（https://www.aqistudy.cn/historydata/）。本研究所使用地理信息資料來源于國家基礎地理信息中心（http://www.ngcc.cn/），文中涉及的中國地圖均基于自然資源部標準地圖服務網站 （http://bzdt.ch.mnr.gov.cn/）下載的審圖號為GS（2019）1823號的標準地圖制作。

本研究使用數據均來源于公共數據庫，不適用倫理審查。

1.2 研究方法

1.2.1 多重共線性 多重共線性是指線性回歸模型中的解釋變量之間由于存在精確相關關系或高度相關關系而使模型估計失真或難以估計準確。因此，為保證回歸模型的合理性，應在構建模型前對備選自變量的共線性進行分析。方差膨脹因子（VIF）是常用的檢測自變量之間多重共線性的指標［17］。本研究將采用VIF對肺結核發病情況與影響因素之間的關系進行共線性檢驗，以避免由于影響因素之間的高度共線性而影響回歸分析結果，其計算公式如下：

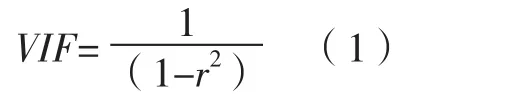
其中，r為線性回歸中的決定系數，反映了回歸方程解釋因變量變化的百分比。VIF越大，說明解釋變量之間存在共線性的可能性越大，若VIF均在0～10，則影響因素之間不存在高度共線性，可直接進行回歸分析［18］。

1.2.2 空間自相關 使用空間計量學方法的前提是樣本數據之間存在空間異質性，因此在構建GWR和GTWR模型前需對自變量進行空間自相關分析。通常使用莫蘭指數（Moran'sⅠ）進行全局空間自相關分析，以確定所研究樣本點的某一屬性值與領域內其他樣本點相同屬性值在空間上是否關聯。本研究將通過計算全局Moran'sⅠ以確定肺結核發病情況的空間自相關性，其計算公式如下：

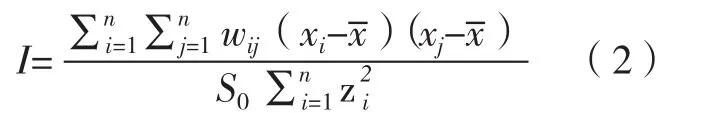
其中，S0為所有樣本點之間空間權重的總和，zi為樣本點i的某一屬性值與其平均值的偏差。Moran'sⅠ的取值在-1～1，若指數為正值則表示樣本的某一屬性值在空間上呈現聚集狀態，且指數越趨近1則聚集程度越強；若指數為負值則表示樣本屬性值呈離散分布；指數為0則表示樣本屬性值呈隨機分布，無顯著特征。

1.2.3 回歸模型構建 本研究分別構建最小二乘法（OLS）模型、GWR模型和GTWR模型對肺結核發病情況進行實證分析，并比較模型優度以確定GTWR模型是否為處理肺結核數據的最佳模型。

OLS模型是常用的傳統線性回歸模型，該模型僅對參數進行了平均或全局意義上的估計，但無法體現各參數在空間上的非平穩性。模型計算公式為：

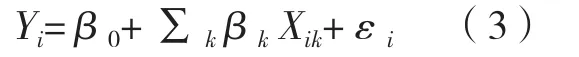
其中，Yi表示第i個樣本點的因變量，β0表示線性回歸方程的截距，βk表示第k個自變量的回歸系數，Xik表示第i個樣本點的第k個自變量，εi表示隨機誤差。

GWR模型是基于傳統線性回歸模型改進后的模型，其主要優勢是能夠將空間權重矩陣運用在線性回歸模型之中，可以更好的展現結果的空間結構分異。模型計算公式為：

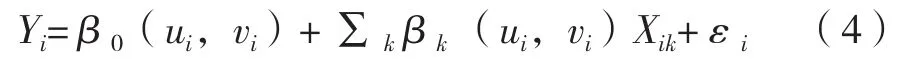
其中，Yi表示第i個樣本點的因變量，ui表示第i個樣本點的經度坐標，vi表示第i個樣本點的緯度坐標，（ui，vi）表示第i個樣本點的空間經緯度坐標，β0（ui，vi）表示第i個樣本點的常數項，βk（ui，vi）表示第k個自變量在第i個樣本點的回歸系數，Xik表示第i個樣本點的第k個自變量，εi表示隨機誤差。

GTWR模型是在GWR模型的基礎上將時間賦值到局部樣本點數據集上，求解局部樣本點i的參數，充分利用樣本數據的時間特性，提高參數估計的準確性。模型計算公式為：

其中，Yi表示第i個樣本點的因變量，ui表示第i個樣本點的經度坐標，vi表示第i個樣本點的緯度坐標，ti表示第i個樣本點的時間坐標，（ui，vi，ti）表示第i個樣本點的時空維度坐標，β0（ui，vi，ti）表示第i個樣本點的常數項，βk（ui，vi，ti）表示第k個解釋變量在第i個樣本點的回歸系數，Xik表示第i個樣本點的第k個自變量，εi表示隨機誤差。

GWR與GTWR模型的參數方法如下：

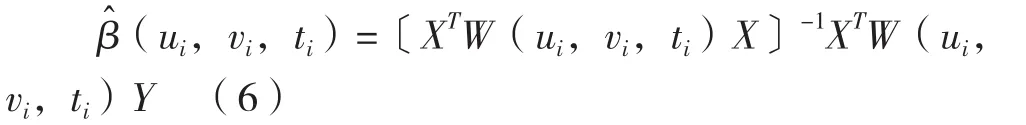
其中，空間權重矩陣W是由空間帶寬、核函數、距離計算公式共同決定。根據既往文獻［7］，本研究將基于最小交叉驗證（CV）值、高斯（Gaussian）核函數和歐式距離（Euclidean distance）來共同構建模型。模型優度通過比較修正后的赤池信息量（AICc）與R2值來評估，R2值越大，AICc值越小，說明自變量對因變量的解釋度越強。

1.2.4 統計分析 使用均數、最小值、最大值、四分位數間距來描述GTWR模型的擬合系數。基于GTWR模型的擬合系數，分別繪制各個變量的核密度圖和時空分布圖。使用自然斷裂點法對相似度較高的數據進行分組，同時強行將“0”設置為區間值，以區分正系數和負系數，當擬合系數為正值時，表示自變量對因變量具有促進作用；當擬合系數為負值時，表示自變量對因變量具有抑制作用，且擬合系數的絕對值越大，作用程度越大。

本研究使用R 4.1.3軟件進行統計描述，使用Arc GIS 10.7軟件進行模型參數估計和模型構建。

2 結果

2.1 肺結核發病情況的時空分布 2016—2018年全國肺結核發病率的空間分布見圖1：我國肺結核總發病率在逐年下降，且空間分布較為集中。肺結核發病率較高的地區主要集中在新疆、四川、西藏、青海、貴州、廣西等。其中，新疆的肺結核發病率連續3年處于最高水平；四川的肺結核發病率在2016年處于較高水平，但隨后2年發病率大幅下降；西藏、青海的肺結核發病率在2016年處于較低水平，但隨后2年發病率大幅增加。肺結核發病率較低的地區主要集中在寧夏、天津、上海、北京、海南等。

圖1 全國肺結核發病率空間分布圖Figure 1 Spatial distribution of pulmonary tuberculosis incidence in China during 2016—2018

2.2 模型對比結果 經過多重共線性和空間自相關檢驗（全局Moran's I= 0.376），剔除氣溫這一具有強共線性的變量（VIFTmax=48.01，VIFTmin=48.34）后，分別建立OLS、GWR和GTWR模型，評估并比較模型優度，結果如表1所示。GTWR模型的R2值與AdjustedR2值均比OLS和GWR模型要高，同時GTWR模型的AICc值均比OLS和GWR模型要小，表明GTWR模型能更好地解釋自變量對肺結核發病情況的影響，更能解釋具有時空特征的數據。

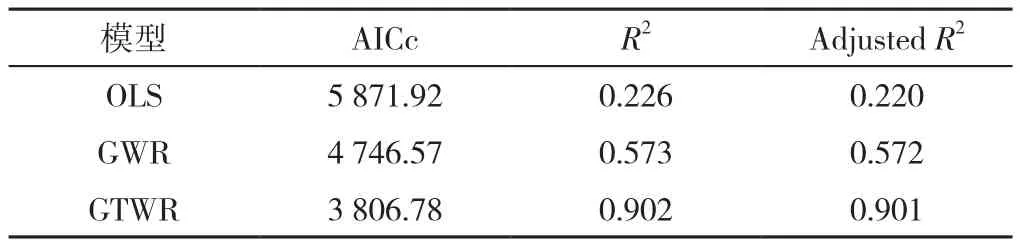
表1 OLS、GWR、GTWR模型比較的結果Table 1 Values of AICc，R2 and adjusted R2 of OLS，GWR and GTWR models

2.3 擬合系數的時空特性 使用均數、最小值、最大值、四分位數間距來描述GTWR模型的擬合系數，結果如表2所示。基于GTWR模型的擬合系數結果繪制每個變量的核密度圖，結果如圖2所示。擬合系數的核密度圖結果顯示：自變量風速呈現多峰分布，主峰約為-0.5；自變量濕度呈現多峰分布，主峰約為0.01，且各峰系數均大于0；自變量PM2.5呈現左偏峰分布，主峰約為-0.01；自變量PM10呈現單峰分布，主峰約為0.005；自變量SO2呈現多峰分布，主峰約為0；自變量NO2呈現多峰分布，主峰約為-0.03；自變量CO呈現右偏峰分布，主峰約為-0.5；自變量O3呈現多峰分布，主峰約為0。

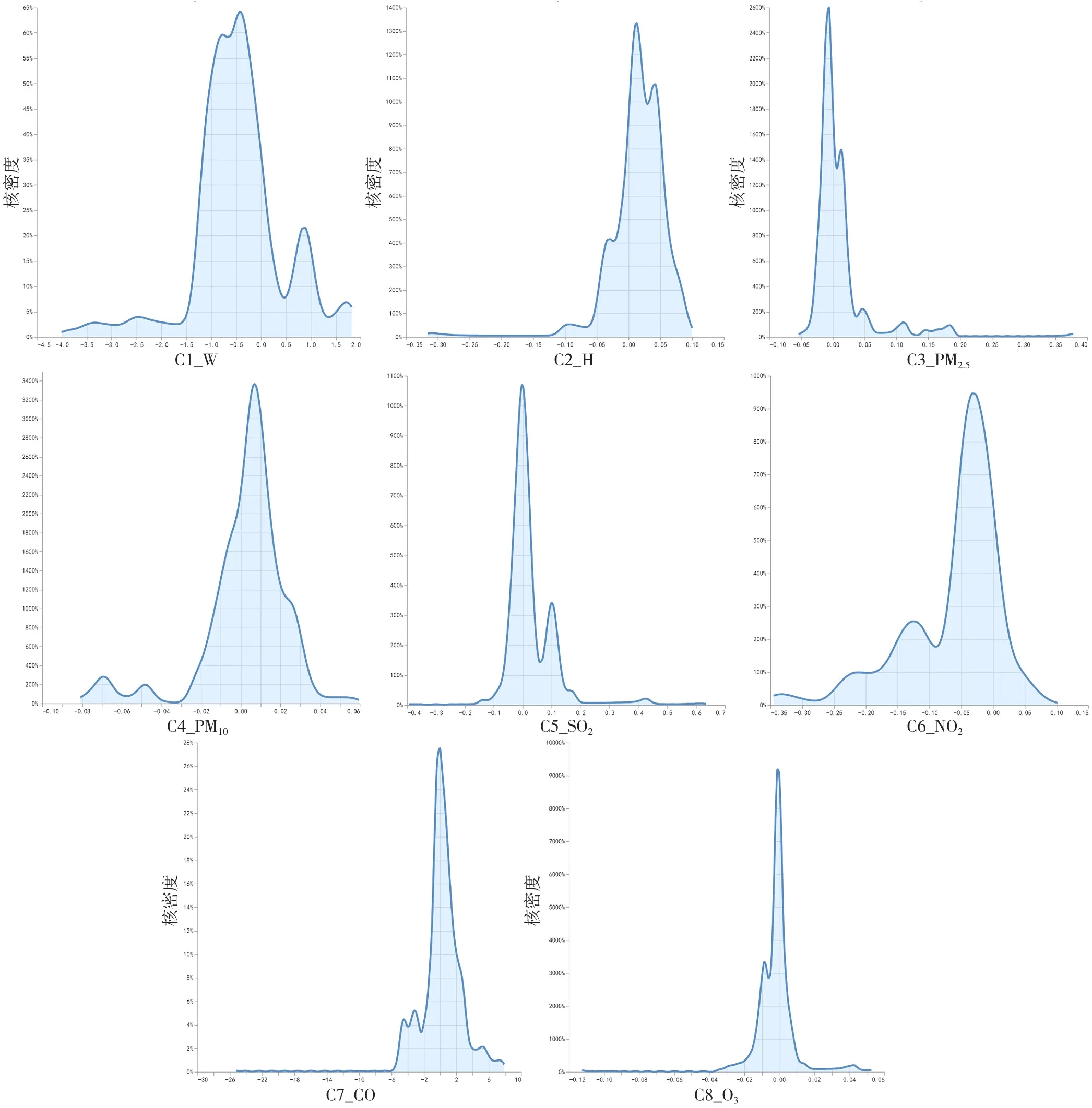
圖2 各變量擬合系數的核密度分布圖Figure 2 Kernel density estimation of fitting coefficients of each variable

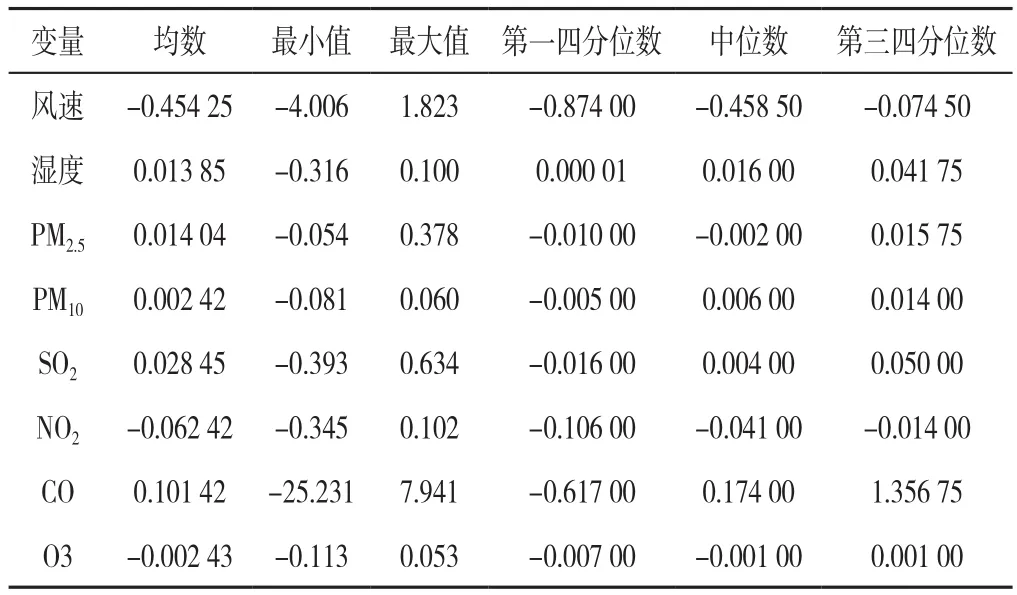
表2 GTWR模型的擬合系數Table 2 Fitting coefficients of meteorological and air quality factors included in GTWR model

基于GTWR模型的擬合系數，分別繪制各個變量的時空分布圖（圖3）。擬合系數的時空分布圖結果顯示：自變量風速呈現中部和東南部的擬合系數較低、東北和西部的擬合系數較高的分布格局，其中風速對青海、甘肅、湖南、江西等地區的肺結核發病率具有顯著的抑制作用，對西藏、新疆、黑龍江等地區的肺結核發病率具有顯著的促進作用；自變量濕度呈現西部和北部的擬合系數較低、東南和南部的擬合系數較高的分布格局，其中濕度對海南、廣東、廣西等地區的肺結核發病率具有顯著的促進作用；自變量PM2.5呈現東北部和中東部的擬合系數較低、西南部和西部的擬合系數較高的分布格局，其中PM2.5對廣西、云南、新疆、西藏等地區的肺結核發病率具有顯著的促進作用；自變量PM10呈現中部和西部的擬合系數較低、東南部和中東部的擬合系數較高的分布格局，其中PM10對浙江、上海、福建等地區的肺結核發病率具有顯著的促進作用；自變量SO2呈現中部和北部的擬合系數較低、西部和南部的擬合系數較高的分布格局，其中SO2對西藏、廣東、新疆等地區的肺結核發病率具有顯著的促進作用；自變量NO2呈現西北部和西南部的擬合系數較低，東北部、中部的擬合系數較高的分布格局，其中NO2對黑龍江、吉林等地區的肺結核發病率具有顯著的促進作用；自變量CO呈現西部和西南部的擬合系數較低、東南部和中西部的擬合系數較高的分布格局，其中CO對福建、青海、甘肅等地區的肺結核發病率具有顯著的促進作用；自變量O3呈現西北部和南部的擬合系數較低、東北部和西南部的擬合系數較高的分布格局，其中O3對新疆、浙江、福建等地區的肺結核發病率具有顯著的促進作用。

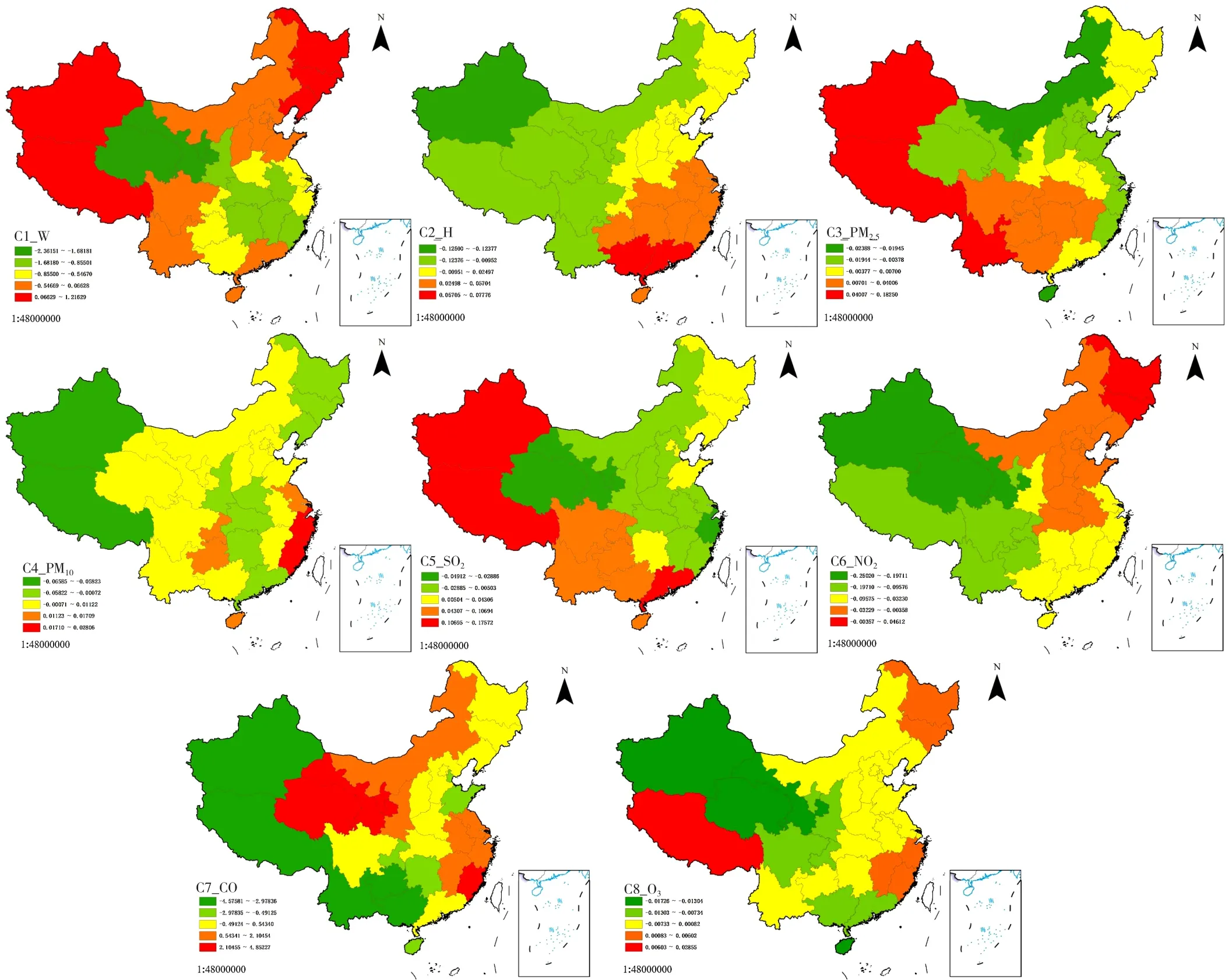
圖3 各變量擬合系數的時空分布圖Figure 3 Spatial and temporal distribution of fitting coefficients of each variable

3 討論

本研究構建模型前預先進行了多重共線性檢驗，結果顯示，自變量氣溫具有強共線性。既往研究也表明氣溫與其他呼吸系統疾病危險因素具有交叉協同效應。馬盼等［19］研究顯示，高溫、高濕共同作用下將對兒童的呼吸系統健康造成更嚴重的后果，而低溫、低濕共同作用下將增加老年人的呼吸系統疾病患病風險。一項基于醫院門診數據的時間序列分析結果顯示，氣溫和各種污染物濃度之間存在明顯的交互作用，尤其是低溫與高濃度污染物共同作用下，對呼吸系統門診就診人數的影響最大［20］。由于多重共線性數據可能會影響GTWR模型分析的精度，本研究未將氣溫這一具有強共線性的變量納入模型。

3.1 各變量擬合系數的核密度分布圖分析 各變量擬合系數的核密度圖結果顯示：自變量風速的主峰系數為負值，且各峰系數有正有負，表明自變量的增加對大多數地區的肺結核發病情況呈現顯著的保護作用，但在部分地區仍具有顯著的促進作用；自變量濕度、SO2的主峰系數為正值，且各峰系數均＞0，表明自變量的增加將顯著促進肺結核發病率的增加；自變量PM2.5、NO2、CO、O3呈現多峰分布，且各峰系數有正有負，表明自變量的增加對大多數地區的肺結核發病率的增加呈現顯著的促進作用；自變量PM10呈現單峰分布，主峰系數為正值，表明自變量的增加將顯著促進大多數地區肺結核發病率的增加。

3.2 各變量擬合系數的時空分布圖分析 GTWR模型的顯著優勢是其擬合系數可以反映自變量對因變量影響的時空變異特征。本研究分別繪制了各變量擬合系數的時空分布圖，結果顯示：自變量風速對青海、甘肅、湖南、江西等城市的肺結核發病率的增加具有顯著的抑制作用，對西藏、新疆、黑龍江等地區的肺結核發病率的增加具有顯著的促進作用。既往研究表明，風速對肺結核發病存在促進作用［21］，較大的風速可降低氣溫，從而間接增加肺結核發病風險。針對本研究的雙向作用，可能存在的原因是：西藏、新疆屬于高海拔地區，東三省的平均氣溫本就偏低，這些地區更易受到風速的影響導致氣溫下降，從而使肺結核發病風險增加，因此這類地區應在大風天氣注意保暖以預防疾病。而湖南、江西等地的平均溫度較高，溫度不易受風速影響，較大風速還會降低其空氣污染物濃度［22］，進而使肺結核發病風險降低。

自變量濕度對海南、廣東、廣西等地區的肺結核發病率增加具有顯著的促進作用。這與既往研究中較高濕度能增加肺結核發病風險的結論相符合［18，21］。可能存在的原因是：在一定范圍內，較高的濕度將增加結核桿菌在空氣中停留存活的時間，從而增加了人群感染結核桿菌的風險。因此，針對這類地區應注意對家具或生活用品的勤加晾曬，盡量保持生活環境的干燥。

自變量PM10對浙江、上海、福建等地區的肺結核發病率具有顯著的促進作用。這與既往研究中PM10暴露濃度增加將導致肺結核發病風險增加的結論相符［23］。可能存在的原因是：PM10等可吸入顆粒物能夠伴隨呼吸進入人體，并在肺部沉積，可能會損傷肺泡及黏膜，導致肺部組織慢性纖維化等情況發生，降低肺部抵抗力；此外，PM10等空氣污染物還可以與空氣微生物結合［24］，明顯增加結核病菌侵入人體的概率。因此，針對這類地區應注意在空氣污染程度較高時避免戶外活動。

既往研究表明空氣污染物（PM2.5、SO2、NO2、CO、O3）的濃度增加會顯著增加肺結核的發病風險［23，25-26］，本研究的大部分結果也能夠與該結論相互驗證。但上述幾類空氣污染物作為自變量也存在部分擬合系數為負數的現象，這部分結果與既往研究結論相悖。造成這一現象的原因可能是：由上述結論可知，擬合系數為負數的城市主要為江蘇、上海、廣東等沿海地區和西藏、新疆、青海等高海拔地區，此類地區的空氣質量較好，空氣污染物濃度較低，因此空氣污染物對于此類地區肺結核發病情況的促進作用不顯著。但模型構建過程中，在與其他地區、其他變量共同分析時，尤其是與空氣質量較差地區做對比，且存在其他保護因素時，此類自變量在承擔部分結果解釋的功能后，最終導致過低濃度的空氣污染物呈現負擬合系數的現象。針對大部分城市的空氣污染物對肺結核發病人數的促進作用，應采取積極措施改善空氣質量，降低空氣污染物濃度；在空氣污染物濃度較高的時候盡量避免外出，在室內即時關窗，以減少接觸空氣污染物，從而降低肺結核發病風險。

本研究存在一定的局限性。第一，為避免新型冠狀病毒肺炎造成的影響，尤其是疫情防控間接導致其他呼吸系統疾病發病率的減少［27］，本研究選取2016—2018年的數據進行分析，所反映的結果可能與當前疫情形勢下的實際情況有所偏差。第二，由于本研究數據存在較強的共線性，可能會導致模型結果存在一定偏差，研究組計劃后續使用更多數據集去驗證模型及研究結果。第三，既往研究顯示，氣象因素與空氣質量因素不僅對當天肺結核發病情況有顯著影響外，還存在3～5 d的滯后效應［23，28］，但本研究因數據局限并未能對其進行驗證。第四，影響肺結核發病情況的因素還包括生活方式、教育水平、經濟狀況等，但由于相關數據缺乏可及性，本研究并未將其納入。因此，研究組計劃后續引入更新、更全面的數據集來提高模型的適用性和穩健性。

本研究基于2016—2018年全國數據構建的GTWR模型很好地展示了中國肺結核發病情況的時空分布，并詳細闡述了氣象因素和空氣質量因素與肺結核發病情況的顯著相關關系及其時空特異性。在實際疾病預防工作中，應結合不同地區的不同影響因素，針對性的制定疾病預防措施。例如：高海拔地區大風天氣注意保暖；濕度較高地區應注意除濕；空氣質量較差地區應積極采取措施改善空氣質量，并注意避免高空氣污染物濃度時的戶外活動。

作者貢獻：趙明揚負責提出概念、數據管理、形式分析、原稿寫作等工作；周乾宇負責方法學、監督審查和編輯寫作等工作；王榮榮、王宗熹、何雯倩、張文森、張恒榛、田卓旸、吳柯、王碧瑤負責數據管理工作；孫長青負責資金支持、項目管理、監督、審查和編輯寫作等工作。

本文無利益沖突。