基于Maple的三鉸斜拱力學分析及矢跨比優化

毛星波，盛冬發，朱 軍

（西南林業大學土木工程學院，昆明 650224）

0 引言

中國作為基建大國，橋梁建設在促進國民經濟發展和提高國民整體生活水平方面發揮了重大作用，拱橋作為一種歷史悠久的橋梁結構在其中扮演著重要的角色。拱橋按受力體系可分為三鉸拱、兩鉸拱和無鉸拱，其中三鉸拱因其良好的適用性與受力性能，在地勢險峻偏遠的地方得到廣泛運用［1］。三鉸拱實用理論的研究主要有力學分析與優化設計兩個方面。在力學分析方面，李彤等［2-3］利用計算機編程求解三鉸拱內力及其影響線，提高了三鉸拱力學分析的精度與效率。夏健明［4］提出利用Excel數據計算及成圖功能繪制三鉸拱內力圖，為三鉸拱內力計算提供了一種新思路。也有學者對三鉸拱的內力計算方法進行了研究［5-6］，或以現代流行語言為三鉸拱內力計算編制相應程序［7-8］。在優化方面，任治章等［9-10］在合理拱軸線的基礎上，推導出均布荷載作用下的三鉸拱最優矢跨比理論解。鄧小康等［11］基于拱圈自重建立微分平衡方程，解得了等截面空腹式三鉸拱合理拱軸線。

上述研究的具體對象皆為三鉸平拱，即兩拱腳處于同一水平高度的三鉸拱，對斜拱方面的研究則甚少。本文對三鉸斜拱一些受力及優化的問題進行分析研究。首先，對豎向均布荷載下三鉸斜拱的合理拱軸線分析求解，并對三鉸斜拱約束反力及內力影響線函數進行推導；其次，建立以內力為目標函數的三鉸斜拱矢跨比優化模型；最后，為便于本文理論在實際工程中的應用，使用Maple符號計算軟件編制相應的計算程序，并通過案例驗證文中理論推導的正確性及優化模型的優化效果。

1 三鉸斜拱合理拱軸線分析求解

以拱的任一截面左邊（或右邊）所有外力的合力（包括數量、方向和作用點）作出合力多邊形，該合力多邊形稱為拱的壓力線。當拱的壓力線與拱的軸線重合時，各截面的彎矩為零，拱處于無彎矩狀態，這時各截面只受軸力作用。此時，使拱處于無彎矩狀態的這一軸線稱為合理拱軸線［12］。由此可知，擁有合理拱軸線的拱橋截面上應力均勻，能充分利用材料強度和圬工材料良好的抗壓性能。

根據合理拱軸線定義，若使三鉸斜拱的截面彎矩方程恒等于零，便有可能解出合理拱軸線函數。設三鉸斜拱在均布荷載作用下截面彎矩恒等于零，其具體受力情況如圖1 所示。

圖1 三鉸斜拱合理拱軸線推導簡圖

故有其任意截面的彎矩方程式

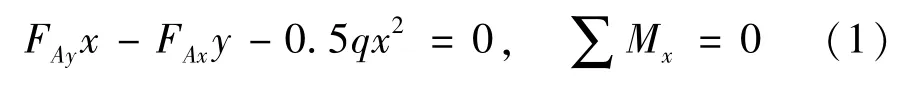
根據圖1，建立B、C鉸點的彎矩平衡方程組，以此解得A鉸點支座水平反力FAx和A鉸點支座垂直反力FAy。將FAx與FAy代回式（1），得其合理拱軸線式

將A、B鉸點拱腳高差h＝0、左右半拱跨長差L1＝0 代入式（2）得：

為三鉸平拱在均布荷載作用下的合理拱軸線表達式［13-14］，表明式（2）對三鉸平拱同樣適用。

2 三鉸斜拱影響線函數推導及內力計算

當一個指向不變的單位集中荷載（通常是豎直向下的）沿結構移動時，表示結構某一指定量值變化規律的圖形，稱為該量值的影響線［15］。在拱橋設計時，利用影響線確定拱橋關鍵截面上某量值的最不利荷載作用位置，并據此求出該量值在設計荷載作用下產生的最大值，以此作為關鍵截面尺寸和形狀設計的依據。因此影響線的確定對拱橋設計至關重要。設三鉸斜拱在單位豎向移動載荷FP作用如圖2 所示，可分別推導支座垂直反力FAy、FBy，支座水平反力FAx、FBx，彎矩MK、剪力QK和軸力NK的影響線函數。

圖2 三鉸斜拱受力計算簡圖

2.1 支座反力影響線的推導

三鉸斜拱與雙鉸拱、無鉸拱具有明顯不同的特征。雙鉸拱、無鉸拱由于多余約束的存在為超靜定結構，而三鉸斜拱解除了多余約束，為靜定結構。鑒于此，使用平衡方程可求解三鉸斜拱支座反力影響線函數。另考慮到單位荷載的移動性，將支座約束反力影響線的求解分為單位荷載在左半拱時和右半拱時兩種情況。依據圖2 建立B、C鉸點彎矩平衡方程組，求解出三鉸斜拱A鉸點支座反力影響線函數如下：

同理，建立A、C鉸點彎矩平衡方程組，可求解出三鉸斜拱B鉸點支座反力FBy、FBx影響線函數。

2.2 內力影響線的推導

拱軸截面內力影響線可用截面法求得。左半拱截面的內力影響線計算簡圖見圖3。圖中：xK、yK為擬求解影響線的截面的形心坐標；φK為該截面處拱軸線傾角，可由拱軸線方程求導得出，其在右半拱時取值為負。另外，圖3 中內力MK、QK、NK所示方向皆設定為正方向。根據圖3，利用截面法對擬求解截面xK位于左半拱時的內力影響線函數進行推導，得內力MK、QK、NK影響線函數如下：

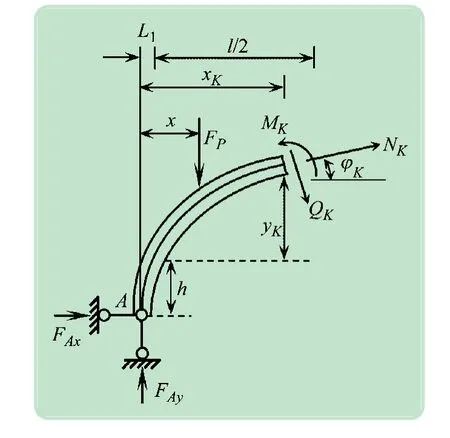
圖3 左半拱內力影響線計算簡圖

同理，通過已知具體表達式的FBx、FBy影響線，可建立起擬求解截面xK位于右半拱時的內力影響線函數表達式。

2.3 三鉸斜拱內力計算

因影響線描述了單位移動載荷作用下某量值的變化規律，故當荷載為集中荷載組或分布荷載組時，這些量值可以根據疊加原理利用影響線求得。考慮利用影響線計算三鉸斜拱相關截面內力，其計算公式為

式中：Z為三鉸斜拱因荷載作用所產生的量值大小，文中為指定截面彎矩MK、剪力QK、軸力NK的大小；FPi為若干豎向集中荷載；yi為與集中荷載相對應的影響線縱標；qx為分布荷載函數；yx為分布荷載相對應的影響線函數。

3 三鉸斜拱矢跨比優化

雖然具有合理拱軸線形的拱橋截面應力均勻，能充分利用材料強度，但實際上拱橋不可能僅受均布載荷作用。此時，式（2）的合理拱軸線函數將變得不再那么“合理”，拱橋截面上也不再只有軸力。為使這種情況下的三鉸斜拱受力更合理，考慮以拱軸各控制點內力平方和為目標函數對其進行矢跨比優化。所建立的矢跨比優化模型如下：

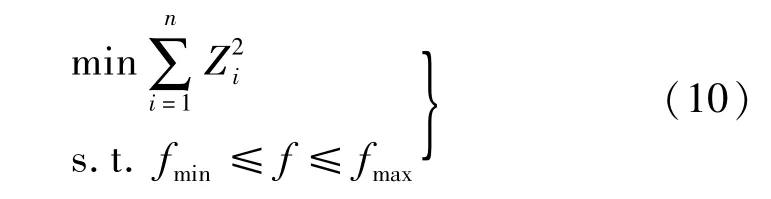
式中：設計變量f為矢高，其上下限值分別為fmax與fmin；Zi為各拱軸控制點處彎矩或軸力，其值大小用含矢高f的函數表示，具體表達式也可通過三鉸斜拱Maple程序快速求得。各拱軸控制點的選取依據以下原則：若以彎矩為目標函數，則以集中力作用點、均布力作用范圍起始點、均布力作用范圍結束點、拱跨等分點為各控制點優先選擇，其盡可能在拱軸線上均勻分布；若以軸力為目標函數，則優先將拱腳、拱頂選作為控制點，然后參考以彎矩為目標函數的選擇方法選擇其他控制點。得到優化模型具體表達式后，可利用數學計算軟件對設計變量進行尋優，得到最優矢高。

4 三鉸斜拱影響線繪制及內力計算的Maple編程

為便于工程實際應用，考慮將文中理論與方法編制成Maple程序，Maple軟件提供的如符號計算、數值處理、二維與三維作圖等廣泛的數學計算功能得到了大量工程師及學者的青睞與使用［16］，故其也是目前世界上最為通用的數學和工程計算軟件之一。Maple 程序編制的流程如圖4 所示（具體代碼可聯系作者獲知）。圖中，拱形已知條件為三鉸斜拱矢高f、跨長L、兩拱腳高差h、左右半拱跨度差L1及擬求解影響線函數的截面的橫坐標，荷載已知條件對于集中荷載，為其載荷作用點橫坐標及載荷大小，對于分布荷載，為其載荷作用范圍起始點、終止點及載荷函數。以上兩已知條件皆由使用者根據工程實際情況輸入。

圖4 Maple程序運行流程

5 計算案例與驗證

通過下面案例驗證本文三鉸斜拱力學推導的正確性及優化模型的優化效果。現已知有三鉸斜拱如圖5所示，其中拱腳高差h＝2 m、f＝4 m、L1＝2 m、l＝12 m。拱圈自重為均布荷載q＝58 kN／m，拱上車輛集中荷載FP1＝70 kN、FP2＝100 kN、FP3＝30 kN，其作用點橫坐標分別為：x＝2 m，x＝6 m，x＝10 m。另外，該三鉸斜拱設計矢高上下限為3.5～4.5 m，且x＝6 m 截面處為關鍵控制截面K截面。

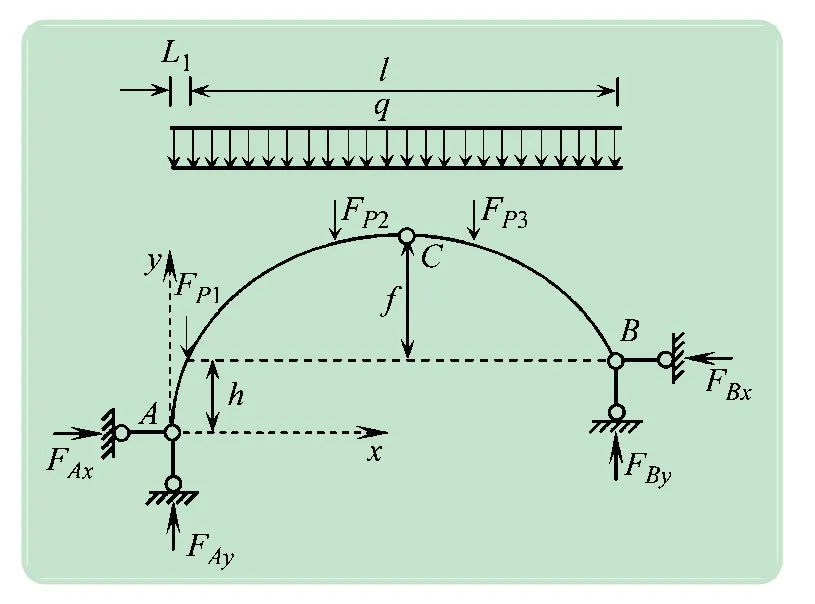
圖5 三鉸斜拱案例

將案例拱形已知條件及拱圈自重荷載代入Maple程序，得到該三鉸斜拱均布自重作用下的各截面內力。將上述內力數據與SAP2000 有限元內力分析結果進行對比，得到圖6。從圖6（a）、（b）知，SAP2000 和Maple對截面剪力及彎矩的分析結果都趨近于0。由此推斷，本文給出的三鉸斜拱合理拱軸線函數是正確的。另外，從圖6（c）可以看出兩者對于軸力的計算結果基本吻合，表明本文Maple 程序對案例截面內力的計算有較好的精度。

圖6 均布自重作用下SAP2000和Maple求解內力對比

使用Maple程序與SAP2000 軟件分別對該案例A鉸點支座反力及K截面影響線進行分析及繪制，得到圖7、8。圖7 中，折線圖為Maple 程序分析所得結果，其下方為SAP2000 軟件分析結果。圖8 布置與圖7 相同，需注意的是，Maple 分析時設定的剪力正方向與SAP2000 軟件相反。觀察兩圖，圖中兩種方法所得的影響線的變化趨勢及極值點特征基本一致。由此可推斷，本文對三鉸斜拱支座反力及內力影響線函數方程的推導也是正確的。

圖7 A鉸點支座反力影響線

圖8 K截面內力影響線

對案例進行矢跨比優化。選取x＝0、2、6、8、10、14 m處截面作控制點，結合所給矢高約束條件，建立以軸力為目標的矢跨比優化模型。通過Maple程序得到優化模型具體表達式，并經數學計算軟件尋優，得到優化矢高f為4.5 m，故其最佳矢跨比為9／28。優化前后的案例截面軸力對比見圖9。由圖9 知，優化后各截面軸力均有所減小，減小最大位置x＝6.5 m 處，減小了9.05%。以上結果說明，本文所提出的矢跨比優化模型取得了較好的優化效果。

圖9 案例軸力N優化前后對比

6 結論

本文根據三鉸斜拱受力特點，對其處于均布荷載下的合理拱軸線及相關影響線函數進行了推導，并以拱軸各控制點內力平方和為目標函數提出了一種矢跨比優化模型，最后編制了與文中理論相對應的Maple程序，得到的主要結論如下：

（1）推導得到了三鉸斜拱合理拱軸線、支座反力及內力影響線函數表達式，對三鉸斜拱的設計與建設有一定指導意義。其函數對于三鉸平拱同樣適用，統一了三鉸拱受力計算公式。

（2）通過案例證明了文中矢跨比優化模型有較好優化效果，為三鉸斜拱的矢跨比優化提供了明確且可行的理論支持。

（3）編制的Maple 程序為三鉸斜拱支座反力、彎矩、剪力、軸力影響線的繪制及截面內力的計算提供了便利。同時，因程序中使用的函數對三鉸平拱同樣適用，故該程序也可用于三鉸平拱相應問題的計算。