《多云的宇宙:物理學未解的七朵“烏云”》

[ 日] 小谷太郎

物理學博士，畢業于東京大學物理學專業，研究領域為宇宙物理學和宇宙探測裝置開發。曾先后在日本理化學研究所、美國宇航局戈達德太空飛行中心、東京工業大學、早稻田大學任職。

《多云的宇宙 :物理學未解的七朵“烏云”》

[日]小谷太郎 著 范丹 譯

北京時代華文書局/2020.3/48.00元

黑洞這種奇妙的“存在”被認為是憑借強大的引力吸入一切的宇宙洞穴。

黑洞來源于阿爾伯特·愛因斯坦（1879—1955）的相對論，但由于過于奇妙，一開始被當作不切實際的空談。劍橋大學教授斯蒂芬·霍金（1942—2018）針對黑洞提出了爆炸性的新說法，即本應該能吸入一切的黑洞會逐漸壓縮，最后發生爆炸。

這是真的嗎？研究者就像發現蜜糖的螞蟻一樣圍繞著新學說展開了激烈的討論，并提出了深刻的問題。如果黑洞會爆炸，那么黑洞內信息丟失的同時，熵也會消失。

熵是什么？為什么它的消失會帶來麻煩？黑洞最終真的會爆炸嗎？

愛因斯坦在各領域都名留青史，但最有名的還是相對論。他于1905 年發表了狹義相對論，又在10 年后發表了廣義相對論，兩者被合稱為相對論，也就是現在最正確的記述時間、空間與引力的物理學理論（不過，判定它不夠全面也是本書的主題之一）。

相對論本身就是奇妙的理論，它所述的黑洞則是其中最不可思議的東西。相對論很快就被人接受了，但相對論所預言的黑洞被研究者們厭惡和否定，直到有相關證據之后才勉為其難地認可了它。

愛因斯坦認為，我們生活中的時間與空間（合稱為“時空”）是時而伸展、時而收縮，具有延展性的東西。

也許你會認為具有延展性的時間與空間前所未見，但時空的伸縮其實很簡單，只要有質量，它就能扭曲周圍的時間，拉伸空間。

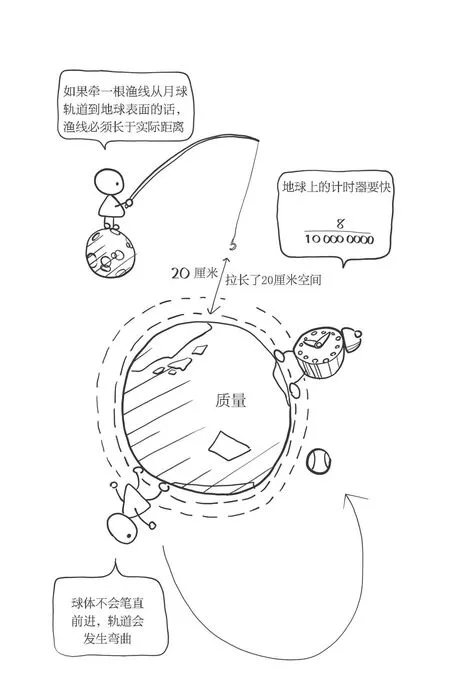
圖1

比如，地球就擁有巨大的質量。時空的伸縮雖然很難用畫來表現，但一定要表現出來的話則如圖1。由于質量附近的時間會緩慢加速，如果在地球表面放置計時器的話，經過計算會發現，與質量的影響為零的情況相比，時間加速了一億分之八左右。也就是放在不受地球影響的遠處的計時器前進一秒，放在地球表面的計時器將前進一秒加一億分之八秒左右。并且，由于地球周圍的空間也會延伸，因此如果牽一根長長的漁線從月球軌道到地球表面的話，除了月球與地球之間本身的長度之外，還需要額外增加約20厘米的漁線。

如果有物體橫穿過具有伸縮性的時空，那么原本筆直的軌道會出現歪斜。月球是以彎曲的軌道繞著地球飛行，蘋果或球體的軌道也是以拋物線落向地面。這就是所謂的引力，也就是愛因斯坦的主張。

換句話說，物體受引力吸引就是在質量的影響下，處于伸縮時空中的物體的前進道路出現了扭曲。相對論被用于計算太陽附近的水星軌道等，并驗證了其正確性。類似太陽附近那樣引力極強的地方，牛頓的萬有引力法不再有效，需要應用相對論。相對論是正確記述宇宙的理論，也是要運用高等數學的難解理論，但一經發表后立刻讓全世界的智者都為之瘋狂。

其中之一就是德國天文學家卡爾·史瓦西（1873—1916），他發現了滿足相對論方程式的一個解法，被稱作史瓦西解，是表示具有質量的“質點”對其周圍的空間制造引力的方程式。在廣闊的宇宙中，地球和太陽也不過是渺小的點狀存在，所以史瓦西解對于計算地球和太陽所產生的引力大有幫助（地球表面計時器和從月球到地球的漁線長度都是利用了史瓦西解來計算的）。

愛因斯坦的廣義相對論發表時正處于第一次世界大戰時期。當時，史瓦西作為軍官奔赴俄羅斯戰場，在戰場上想出了史瓦西解并寫信告訴了愛因斯坦。但不久后，史瓦西因皮膚病惡化而去世。他所留下的解法很久以后也被稱之為黑洞。如果史瓦西能活得更久一點，毫無疑問會對黑洞研究做出不凡的貢獻，他也是被戰爭所摧毀的珍貴天才之一。

史瓦西解和研究質點自轉的“克爾解”等相對論，是闡述引力場中心及質點周圍的時空極度扭曲的解法。

處于極度扭曲時空中的物體的動態只能用不可思議來形容。做墜落運動的物體越是接近質點，通過時間越是扭曲，并且空間延伸。因此，當物體落到距離質點的某個位置時，墜落將會停止。

也許你會認為“怎么可能”，當時的研究者在聽聞這一結論時的反應也和你一樣。

墜落停止的位置被稱為“史瓦西半徑”或“現象的地平線”，它能產生各種超出常識的狀況。比如，位于史瓦西半徑時“逃逸速度”會達到光速。

所謂逃逸速度，是指以該速度拋出球體后擺脫引力飛向無限遠方的速度。根據投球的具體情況能測出該場所的引力，地球表面的逃逸速度約為11 千米/秒，低于該速度的球體很快會因為地球引力落回地面，而超過11 千米/秒的話，球體將飛向宇宙的另一端。

當位于史瓦西半徑內側時，逃逸速度將超過光速。由于超光速的物體不存在于這個世界，所以無論以多大的力道在史瓦西半徑內側投球，最終都只會劃出一道弧線飛向質點附近。由于光也會被折返，所以從外側觀測的話，質點就是半徑等于史瓦西半徑的漆黑圓球（至少當時是如此認為）。

觀測地球和太陽附近并不會發現物體停止落下或光折返的異常現象，是因為地球或太陽比出現奇怪現象的史瓦西半徑大得多。