彎扭作用下橢圓鋼管混凝土構件有限元分析

董 帥，范秀瑛，劉志偉

（中國礦業大學（北京）力學與建筑工程學院，北京 100080）

由于ETFC具有良好的力學性能和流暢的外觀，其在實際工程中得到了廣泛的運用。目前對其研究主要集中在單一受力的狀態，例如：軸壓、偏壓、受彎等情況。但是在實際結構中構件不可能只承受單一的荷載，大部分情況下處于復合受力狀態，目前對于ETFC在復合受力狀態下的研究相對較少，僅文獻［1-3］對其進行研究。其中彎扭作用作為復合受力的一種情況，由于其受力情況比較復雜并且在實際結構中出現的情況較少，少有研究者對其進行研究。但是對彎扭作用進行研究能夠為更為復雜的壓彎扭研究提供理論基礎，并且當ETFC構件作為基礎樁和輸電桿時，其在彎扭作用下的力學性能也是十分重要的，因此對其進行深入的研究十分有必要。

本文通過有限元軟件ABAQUS建立橢圓鋼管混凝土構件在彎扭作用下的數值模型，研究不同加載路徑對其荷載-位移曲線以及相關曲線的影響，對其受力過程進行總結，研究不同參數對其力學性能及相關曲線的影響。

1 有限元模型

1.1 材料模型

橢圓鋼管混凝土構件有限元模型主要由鋼管、混凝土、墊板三者構成。根據文獻［4］的研究選用二次塑流模型作為鋼管的本構，如圖1，式（1）所示。

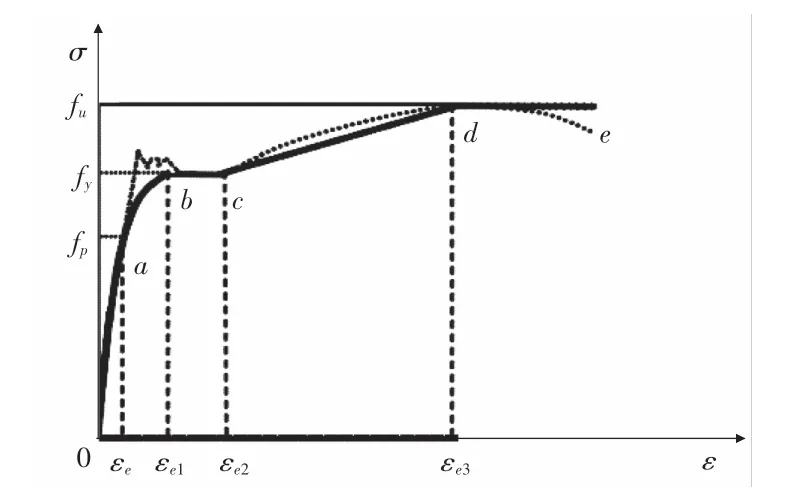
圖1 鋼材的應力-應變曲線

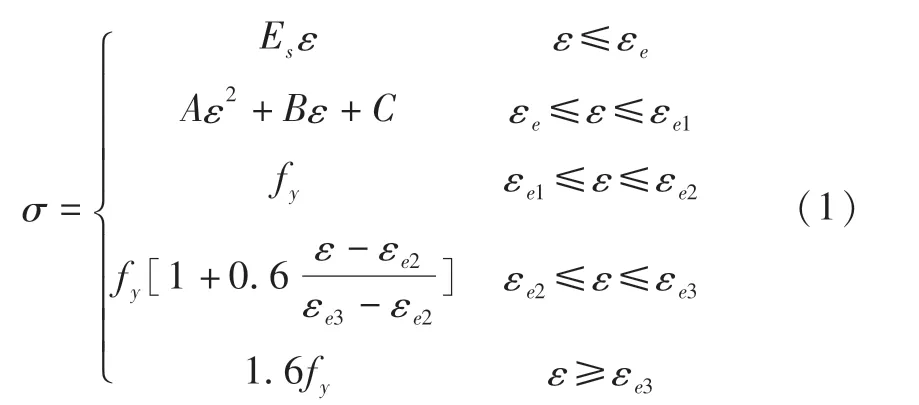
其中，A=0.2fy/（εe1-εe）2；B=2Aεel；C=0.8fy+Aε2e-Bεe；Es為鋼材的彈性模量；fy為鋼材屈曲強度；εe為鋼材比例極限對應的應變，εe=0.8fy/Es；εe1，εe2均為塑性段對應的應變；εe3為強化段對應的應變，其中εe1=1.5εe，εe2=15εe，εe3=150εe。

由于目前缺乏ETFC構件的混凝土本構關系研究，僅文獻［1］和文獻［6］提出等效半徑公式。采取文獻［1］基于摩爾-庫侖模型提出的等效半徑，如式（2）所示，將橢圓混凝土等效為圓形混凝土和矩形混凝土。文獻［1-3］利用此等效半徑取得了較好的模擬效果。

劉威［5］在總結以往研究者成果的基礎上，通過大量算例的計算分析，修正素混凝土單軸應力-應變關系曲線峰值應變和下降段，考慮約束效應ξ和混凝土強度f′c的影響，提出適用于有限元分析的核心混凝土單軸應力-應變關系，如式（3）所示。

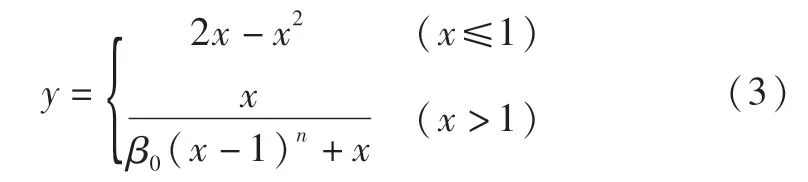
其中，εc=（1 300+12.5f′c）×10-6，x=ε/ε0，y=σ/σ0，σ0=f′c，ω=2，β0=（2.36×10-5）［0.25+（ξ-0.5）7］×（f′c）×0.5≥0.12，ε0=εc+800ξ0.2×10-6。

1.2 有限元分析模型

構件主要由端板、鋼管和核心混凝土組成，如圖2所示。其中端板采用剛體Discrete Rigid模擬，橢圓鋼管采用S4R單元模擬，核心混凝土采用C3D8R模擬。

圖2 彎扭作用下有限元分析模型

鋼管和混凝土之間的相互作用采用表面與表面接觸，法向方向定義為 “硬接觸” ，切向方向定義為罰函數，根據文獻［6］的研究，摩擦系數設置為0.3。端板與鋼管、混凝土采用TIE接觸。底部約束所有方向的位移，頂部是自由端。

2 試驗檢驗

由于缺乏彎扭作用下橢圓鋼管混凝土構件的試驗數據，采用文獻［7-8］提供的ETFC構件在軸壓作用下的試驗數據檢驗模型的準確性，表1給出試件的幾何參數和材料參數，試驗數據和數值模擬結果的對比發現其吻合度較好，說明ETFC構件的數值模型的合理性比較好。

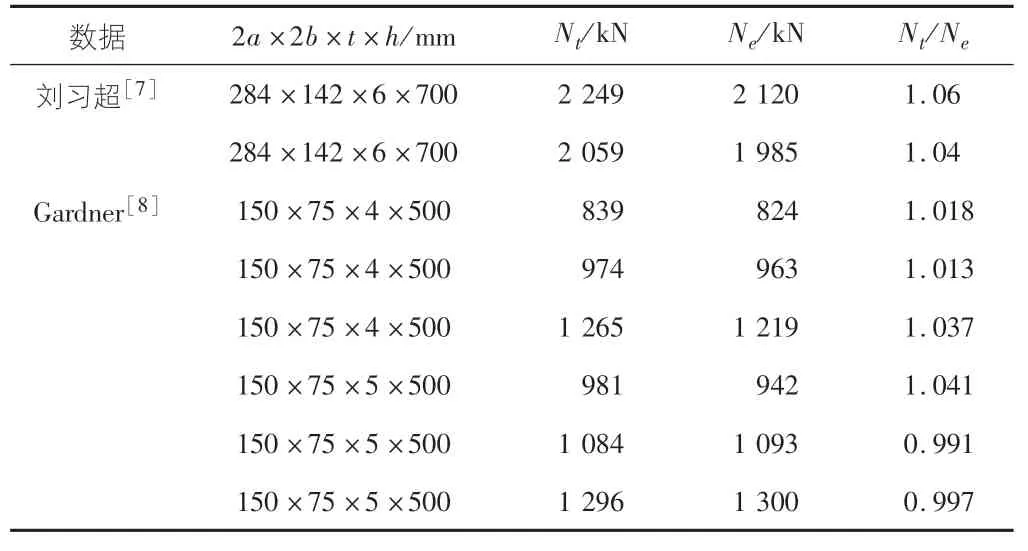
表1 ETFC在軸壓作用下試驗結果和數值模擬比較

3 加載路徑的影響

文獻［9］給出彎扭作用下三種加載路徑，如圖3所示。加載路徑Ⅰ是先施加彎矩M，保持M的大小和方向不變，再不斷施加扭矩T。加載路徑Ⅱ是按照一定彎扭比施加M和T。加載路徑Ⅲ先施加扭矩T，保持T的大小和方向不變，再不斷施加M。

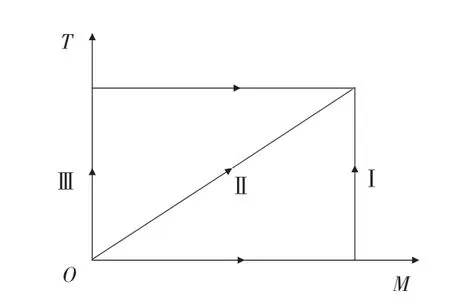
圖3 彎扭作用下加載路徑

標準構件混凝土強度為C40，采用2a×2b×t×h=180 mm×150 mm×3 mm×500 mm，鋼材強度Q345。

3.1 加載路徑Ⅰ

加載路徑Ⅰ是先施加彎矩M，保持其大小和方向不變，再逐步施加扭矩T。根據文獻［9］的研究，構件表現出純扭的破壞特征，因此可按純扭構件的抗扭強度指標確定彎扭構件的極限承載力。

根據圖4，表2可以看出彎扭作用在長、短軸的荷載-位移曲線的變化趨勢基本相似，彎矩變化對彈性階段剛度影響程度較小，但對ETFC抗扭承載力影響較大。隨著M/Mu的增大，ETFC的抗扭承載力下降明顯。當M/Mu較大時，構件承受彎矩較大，因此承受的扭矩會變小，曲線出現下降段，但由于構件塑性較好，所以下降程度較小。

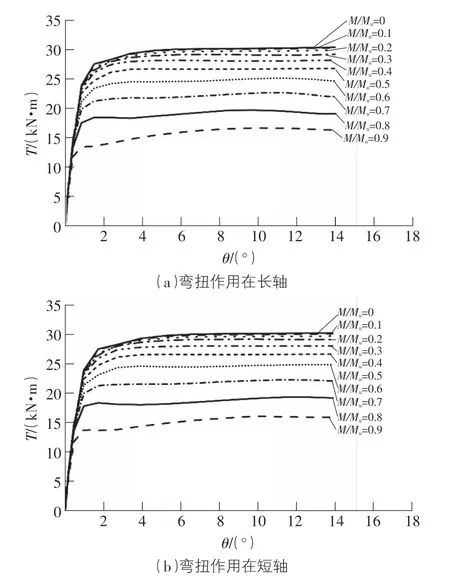
圖4 加載路徑I下T-θ曲線

表2 加載方式Ⅰ彎扭作用下長、短軸承載力比值

ETFC在彎扭作用下的荷載-位移曲線可以分為三個階段：彈性階段、彈塑性階段、塑性階段，如圖5所示。

圖5 加載路徑I彎扭作用下T-θ曲線

1）彈性階段。

在不同彎矩的作用下，構件在彈性階段的彈性剛度基本保持一致，到達A點時，鋼管達到比例極限。此時，受壓區鋼管和混凝土相互作用較小，鋼管和混凝土均為單向受壓，雙向受剪；由于受到混凝土的限制，受拉區鋼管產生拉應力。

2）彈塑性階段。

隨著彎矩增加，核心混凝土承受的應力繼續增加，但由于混凝土的存在，鋼管不會出現局部變形，當到達B點表示鋼管在應力最大處發生屈服。

3）塑性階段。

過B點之后，受壓區的鋼管發生屈服，受壓區混凝土在縱向應力作用下，橫向變形不斷增加，當混凝土橫向變形超過鋼管橫向變形時，則兩者之間產生相互作用力。

3.2 加載路徑Ⅱ

加載路徑Ⅱ是按照一定的彎扭比施加彎矩和扭矩。這是接近真實情況的一種加載方式。根據文獻［9］，加載路徑Ⅱ要根據彎扭比的大小來確定構件是扭轉變形還是彎曲變形，當彎扭比較大時，以截面纖維最大剪應變接近10 000με對應的荷載作為承載力指標，當彎扭比較小時，以截面纖維最大拉應變接近10 000με對應的荷載作為承載力指標。

根據圖6，表3可知，隨著M/T的增加，構件的極限承載力不斷降低，彎扭比對彈性階段線彈性剛度的影響較小。彎扭作用在長、短軸的T-θ曲線的趨勢是相似的，相較于長軸，在M/T相同的情況下，作用在短軸時，抗扭承載力較小。和加載路徑Ⅰ相比，加載路徑Ⅱ的T-θ曲線可以分為三個階段：彈性階段、彈塑性階段和塑性階段。各階段的工作性能與加載路徑Ⅰ相似。

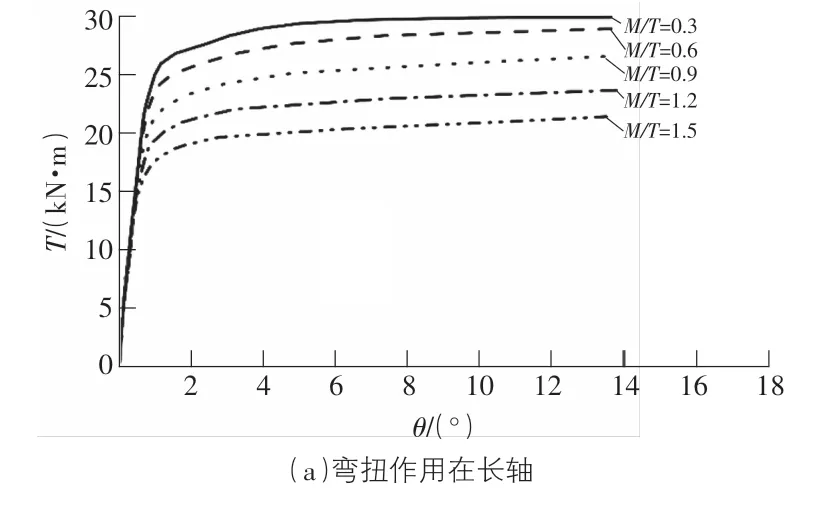
圖6 加載路徑Ⅱ下T-θ曲線

表3 加載路徑Ⅱ彎扭作用下長、短軸承載力比值

3.3 加載路徑Ⅲ

加載路徑Ⅲ是先施加扭矩T，保持T大小和方向不變，再施加彎矩M。對于加載路徑Ⅲ，構件表現為純彎構件的破壞特征，此時選取截面纖維最大拉應變10 000με對應的荷載為承載力指標。

通過圖7，表4可以看出，加載路徑Ⅲ作用下，彎扭作用在長、短軸的M-θ曲線其趨勢基本相似，T/Tu的變化對于其彈性階段的剛度影響較小，但是隨著T/Tu的增大，其抗彎極限承載力不斷減少。在扭轉比相同的情況下，作用在長軸產生的抗彎承載力大于作用在短軸產生的抗彎承載力。

表4 加載路徑Ⅲ彎扭作用下長、短軸承載力比值

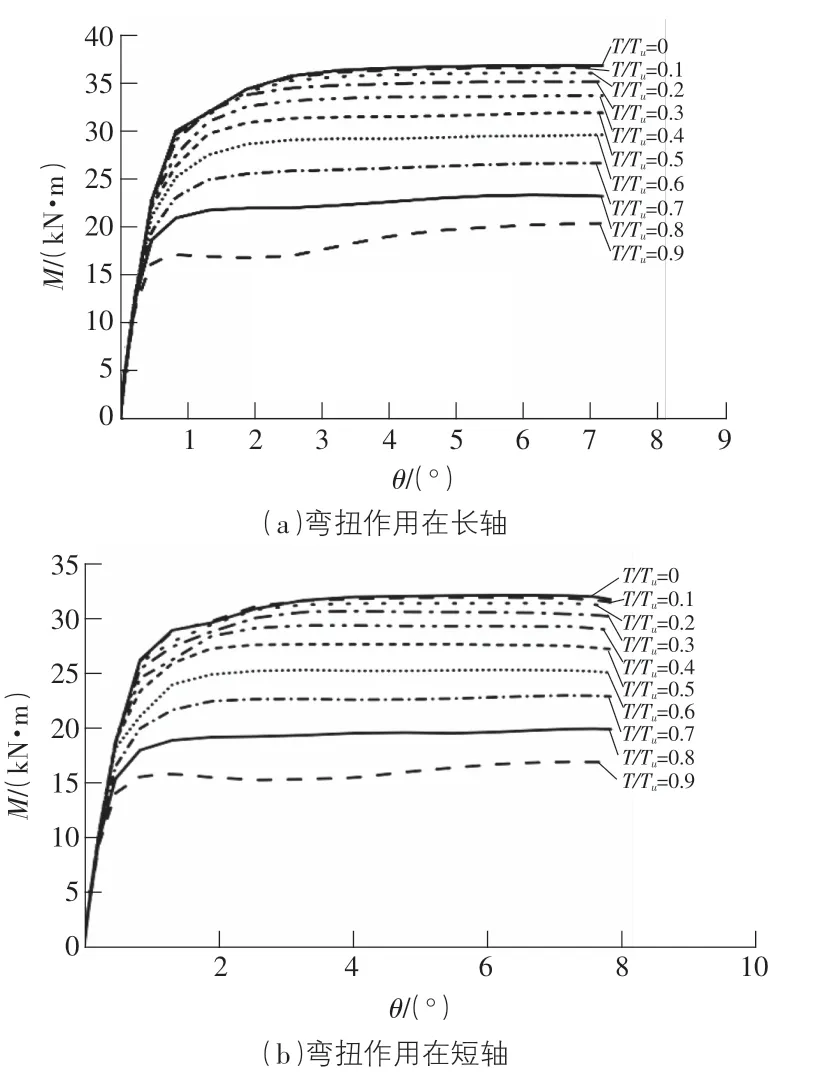
圖7 加載路徑Ⅲ下M-θ曲線

根據圖8研究發現，三種加載路徑對于彎扭構件的M/Mu-T/Tu的相關曲線影響不大，三條曲線的重合度較好，隨著M/Mu的增大，T/Tu也隨之減少，說明加載路徑對構件承載力的影響較小。

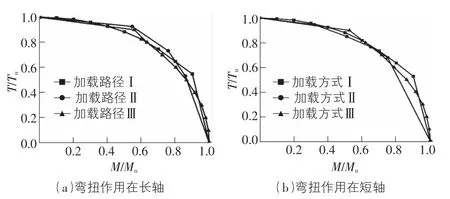
圖8 三種加載路徑彎扭構件M/Mu-T/Tu相關曲線

4 參數分析

根據第3節的結論發現加載路徑對于ETFC構件的荷載-位移曲線的影響程度較小，因此選用加載路徑Ⅲ對ETFC構件在彎扭作用下的力學性能進行參數分析。標準試件選用2a×2b×t×h=180 mm×150 mm×3 mm×500 mm，鋼管強度為Q345，混凝土強度為C40，表5給出橢圓鋼管混凝土構件在彎扭作用下參數分析的具體取值。

表5 橢圓鋼管混凝土構件在彎扭作用下試件尺寸

4.1 鋼管強度

根據表6，表7可知，隨著鋼管強度的增加，抗彎承載力不斷增加。作用在長軸時，Q420的抗彎承載力相較于Q235的抗彎承載力提高了63%左右。作用在短軸時，Q420的抗彎承載力相較于Q235的抗彎承載力提高65%左右。這是因為在混凝土強度不變的前提下，鋼管強度的提高導致其對于混凝土的緊箍力增強，因此構件的抗彎能力增強。根據圖9發現對于不同鋼管強度的相關曲線其趨勢相似，鋼管強度的變化對于曲線趨勢的影響較小，整體曲線隨著T/Tu的增大而減少。

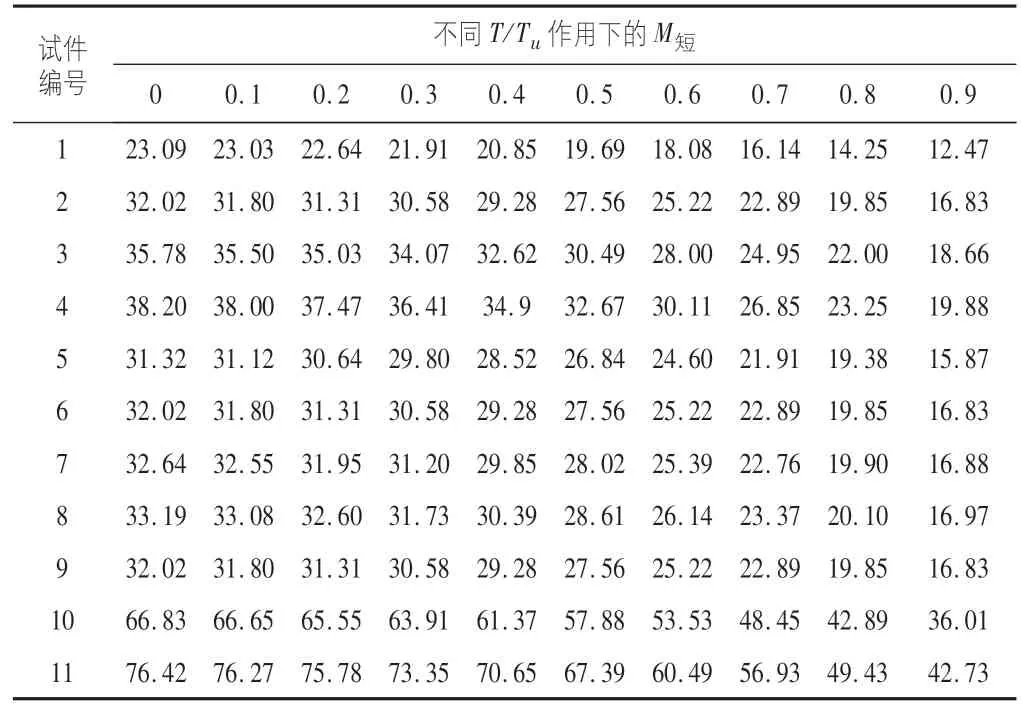
表6 彎扭作用在短軸不同參數構件極限承載力值

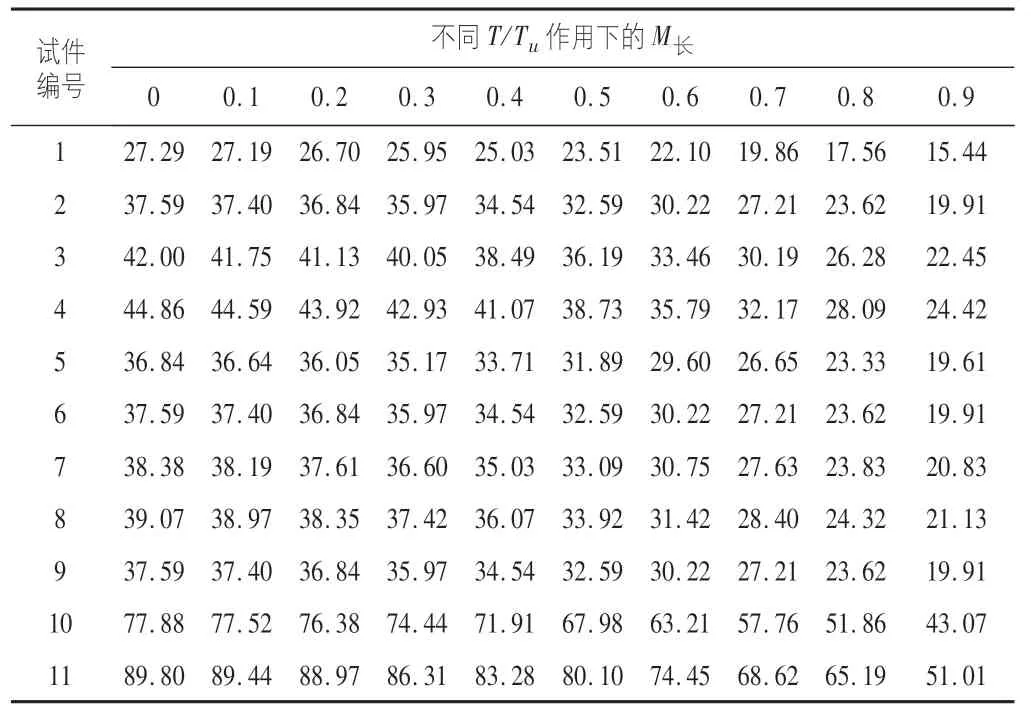
表7 彎扭作用在長軸不同參數構件極限承載力值

圖9 不同鋼管強度下T/Tu-M/Mu相關曲線

4.2 混凝土強度

根據表6，表7發現，隨著混凝土強度的提高，相同T/Tu下，構件抗彎承載力有所增強。對于作用在長、短軸的構件，C60構件的抗彎承載力相較于C30的抗彎承載力提升幅度相對較小。因此可以看出混凝土強度的提升對于相同扭轉比作用下的抗彎承載力的提升程度有限。根據圖10可以發現不同混凝土強度下的T/Tu-M/Mu相關曲線的趨勢相似，混凝土強度增強對于T/Tu-M/Mu曲線的影響較小。隨著扭轉比的增大，構件彎矩比減小。

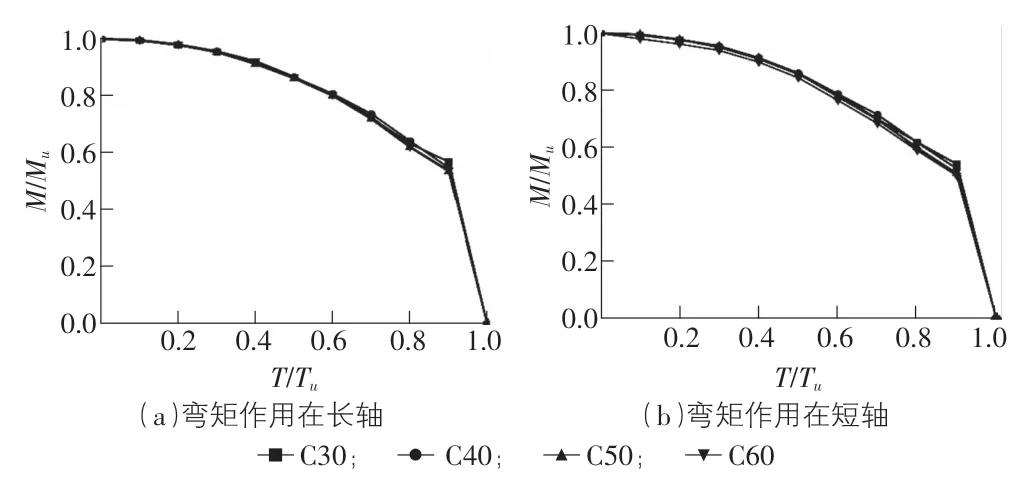
圖10 不同混凝土強度下T/Tu-M/Mu相關曲線

4.3 鋼管厚度

根據表6，表7發現，隨著不同鋼管厚度增大其極限承載力也在不斷增大。對于長、短軸而言，厚度為9 mm的構件相較于厚度為3 mm的構件其極限承載力大大提升。說明鋼管厚度的增大對于ETFC構件在彎扭作用下的極限承載力提高具有顯著作用。根據圖11可知，鋼管厚度的增大對于T/Tu-M/Mu相關曲線的影響程度較小，隨著T/Tu的提高，M/Mu不斷減少。

圖11 不同鋼管厚度下T/Tu-M/Mu曲線

5 結論

1）不同加載路徑對橢圓鋼管混凝土構件在彎扭作用下受力情況影響程度較小，對構件彈性階段的彈性剛度影響較小，隨著施加荷載的增加，其承載力不斷減少。長軸的承載力大于短軸的承載力。2）根據研究發現，不同加載路徑的受力階段大致可分為三個階段：彈性階段、彈塑性階段、塑性階段。3）對加載路徑Ⅲ進行參數分析發現，隨著鋼管強度、混凝土強度、鋼管厚度的增加，其承載力在不斷的提高，鋼管強度、厚度的增加對其承載力的影響較大，混凝土強度對其承載力的影響較小，并且不同參數變化對T/Tu-M/Mu相關曲線影響程度較小。