基于長程設計的小學數學起點型核心知識凸顯式教學*

黃紅成

數學核心知識是具有較強解釋能力、生長能力和遷移能力的數學知識，通常表現為數學概念、運算規律及其蘊含的數學思想方法等，其中扮演知識框架承重點、發散點、發生點和連接點等角色的即為數學起點型核心知識。由于這些核心知識是高度概括、合理簡化和科學遴選的結果，所以教師教學時需要著眼總體進行長程設計，采用凸顯式的教學方法來挖掘其內涵，以顯現其地位和價值。

一、長程設計、凸顯式教學與數學起點型核心知識

長程設計也可以稱為整體設計、總體設計等，可以看作各個階段設計的集中和不同過程設計的整合。對數學起點型核心知識來說，長程設計是指依據知識之間存在的內在邏輯關系和學生的階段認知特征設計的長線教學過程。長程設計關注落實過程中知識教學目標達成的階段性，也注重知識教學前后或整體的一致性，是教學目標階段性和一致性的統一。

凸顯即清楚地顯露。凸顯式教學是一種將知識的表征、內涵等予以直觀呈現，以突出知識的本質和內涵，并能讓學生掌握和領悟的教學方式。凸顯式教學的表現形式多樣，聚焦核心問題、放大教學環節、拉長教學過程等是其主要形式。數學起點型核心知識多表現為抽象、濃縮或簡化后的知識、概念、思想、方法等，在數學知識序列中發揮著貫通前后、承上啟下等作用，通常需要以文字、圖形、符號、式子等形式將其凸顯出來，以引起學生的重視。

概言之，數學起點型核心知識的教學，不僅需要長程設計、整體設計和階段設計、過程設計，也需要在起始階段或獨立教學中通過拉長教學過程、增設教學環節、凸顯知識本質等，著力于起始階段教學目標的設置和達成，講求起始教學的階段性和整體設計的一致性，為促進學生的知識生長、能力孕育、思維進階等提供可能和支撐。

二、基于長程設計的小學數學各領域起點型核心知識的凸顯式教學

1.在圖形教學的概念分析中開展凸顯式教學

數學概念是數學起點型核心知識的主要表現形式之一，也是圖形教學中最常見的內容，是學生判斷和解決問題的重要依據，對學生后續學習中的數學認知和數學理解具有一定的支撐作用。在數學概念教學中采用凸顯式的教學方式，是提高數學起點型核心知識教學實效的一條重要路徑。

以“高”這一概念的教學為例。學生通常認為“高”是垂直方向點（或面）到點（或面）之間的距離，這與圖形中的“高”可以看作一條特殊位置的線段（即“兩個特定點之間的距離”）有一定差異。蘇教版教材首次揭示“高”的概念是在四下《認識三角形》這節課中，借助人字梁讓學生結合已有知識經驗判斷和認識“高”。學生根據人字梁中高的“樣子”概括出高的定義——“從三角形的一個頂點到對邊的垂直線段是三角形的高”。如此操作，學生對高的理解仍然不夠深入。教師教學時可以增設以下類似環節：（1）動態演示。先將人字梁抽象成三角形并引出高（保留高），然后將三角形旋轉，在旋轉過程中采用定格的方式讓學生積累“頂點和底邊發生變化，高的位置也會發生變化”等認識。（2）對應“點”“邊”。讓學生找出對應的頂點和高，依次出示圖1和圖2，讓學生知道“每個頂點都有固定的底邊，每條底邊也有對應的頂點”。（3）變式教學。只改變底邊的長度或只移動頂點的位置，讓學生知道“底邊位置確定了，頂點的位置不同，高往往不同”“底邊的長度不同，但是頂點的位置不變，高可能相同”等。

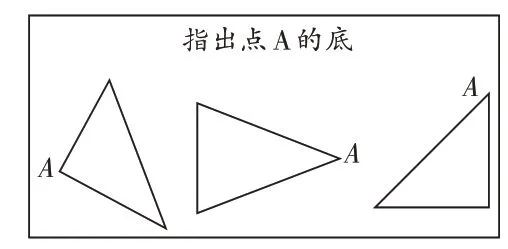
（圖1）

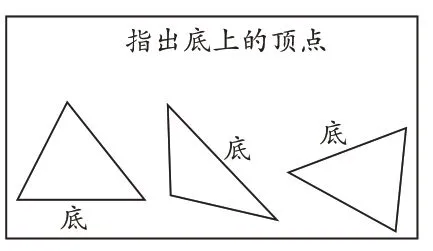
（圖2）

上述教學中的每個環節都針對高的內涵而設計，前兩個環節是讓學生學會判斷高，不僅為學生畫高打下了堅實的認知基礎，也為他們后續學習立體圖形中的高作好了鋪墊；第三個環節有助于強化高的表象，豐富學生對高的外延的認知。這樣，既能凸顯高的本質（兩個特定點之間的距離），也為學生在后續學習中自覺運用已有知識來同化或順應其他圖形中“高”的意義打下了基礎，實現了數學起點型核心知識的內涵和本質在長程學習中的一致性。

2.在運算教學的意義認知中開展凸顯式教學

運算的意義是數學起點型核心知識的重要組成部分，是運算教學的核心內容，教師教學時需要讓學生準確把握運算意義的內涵，展現數學起點型核心知識的順應、同化、遷移等作用，凸顯式教學有利于上述諸多教學目標的達成。

以“除法的意義”的教學為例。長線審視，小學層面關于除法的教學與應用大致可分為三個階段——除法意義的教學和整數范圍內除法的應用、小數除法的意義及應用、分數（百分數）除法的意義及應用。其中，真正有助于學生建立除法意義的是整數階段的教學，后面兩個階段多為引導學生借助對乘法和除法之間的關系以及問題解決經驗的認識來學習除法問題。在教學中，學生在整數范圍內關于除法意義的認識比較清晰，當教學對象擴展到小數和分數領域，他們對除法的理解和應用經常出現困難，在解決類似“1.5千克小麥可以磨1.2千克面粉，照這樣計算，磨1千克面粉需要多少千克小麥？”的問題時，往往會顯現出對除法意義認知的混亂。為此，教師教學“平均分”之后，可以結合教材編擬的“6個小朋友坐纜車，每車坐2人，要坐（ ）車”等問題，讓學生用小棒代替小朋友來表示題意，再根據題意理解除法算式的意義，然后進行如下即時練習：一是根據前面“平均分”的學習素材和問題，思考“6÷2”可以表示怎樣的問題并舉例說明，讓學生將內化的除法意義進行外顯，豐富他們關于除法意義的數學表象和認知，為其運用除法意義進行判斷或解決問題建立認識支撐；二是比一比平均分的對象的個數和平均分的份數、每份的個數，讓學生在學習的起始階段認識到“平均分的對象的個數不少于平均分的份數或每份的個數”，關注除法各部分之間的大小關系，從不同維度感受和認識除法算式，強化其對除法意義的認識。

3.在統計教學的引入環節開展凸顯式教學

統計教學是數學教學的重要組成部分，學生數據意識的形成與發展是統計教學的核心問題，需要教師精心創設凸顯數據分析的教學情境，促進學生理解統計知識的作用。

以“分段整理”的引入為例。“分段整理”是在學生學習了簡單數據或對象的整理和統計方法之后，對數據區間較大的統計對象進行的分析和整理，通常置于復式統計圖的教學之前，因而這節課可以看成數據意識培養的起始課題。如果依照教材按部就班地出示原始數據后直接進行統計方法的教學，學生雖然可以掌握整理的方法，但對于“為什么要分段整理？”“為什么這樣分段？”等問題往往會一頭霧水，難以感受到分段整理的意義，也難以形成數據意識。教師教學時不妨設置如下兩個問題——（1）出示學校鼓號隊員集體照，提問：學校準備給24名鼓號隊員購買服裝，需要考慮哪些問題？依據什么來購買服裝？交流時，基于學生的回答明確“根據隊員的身高來購買比較合適”和“根據隊員的身高來確定服裝的型號”；（2）出示鼓號隊員的身高數據，追問：鼓號隊有24名隊員，他們的身高有高有矮，是不是需要給每個隊員確定一種型號呢？由于問題不切實際，所以學生紛紛回答“不可能”。“既然不能一個身高定一種型號，那么該怎樣來確定型號呢？”學生能夠根據生活實際想出“將130幾厘米、140幾厘米、150幾厘米等分別定為一種型號”的方法，然后再進行數據整理。上述情境中，學生在考慮購買服裝的相關因素時，需要結合生活實際進行分析，認識到不同的身高需要購買不同型號的服裝，并且“不可能有一種身高就來確定一種型號”，進而產生對原始數據進行“分類和整理”的需要，使得分段整理的出現顯得順理成章。可以說，上述凸顯式教學既啟發了學生的數學思維，培養了學生的問題解決能力，又有助于學生數據意識的發展。

4.在“綜合與實踐”教學中就推理能力培養開展凸顯式教學

“綜合與實踐”領域涵蓋的數學起點型核心知識較多，涉及各種思維方式、思想方法等的教學和運用。分析現行的數學教材，數學核心知識的運用顯得單一而突出，每個課題都可以看作教學數學核心知識的起點課題，因而在“綜合與實踐”教學中，需要格外重視數學起點型核心知識的凸顯與教學。

以推理為例，其廣泛應用于問題解決和規律探索的教學環節。在“綜合與實踐”領域，著力培養學生推理能力的課題，首屬蘇教版四下的《一億有多大》。教材的編排突出了推理的思維和方法，讓學生通過說一說、數一數、量一量、稱一稱等四個不同類型的實踐活動，根據數100本練習本的時間、10枚1元硬幣摞在一起的高度、100粒大米的質量來推測“一億的大小”。可謂素材豐富、類型多樣，可以讓學生對“一億”的認知豐富而立體，但正因為多樣，分別從時間、長度和質量等維度來幫助學生建立“一億”的大小概念，三者之間沒有交叉與聯系，也使得學生對這些知識的掌握顯得過于獨立，難有深度的認知和多維的建構。因此，教師教學時可以合理挑選一個活動環節來培養學生的推理能力。譬如，根據10枚1元硬幣摞在一起大約高2厘米，讓學生依次推算100枚、1000枚、10000枚、100000枚……100000000枚1元硬幣摞在一起的高度，然后給予學生充足的時間來思考、交流200枚、3000枚、40000枚、500000枚等數量的1元硬幣摞在一起的高度。而后隱去一些數量的高度，突出教材中這些數量的1元硬幣摞在一起的高度（如圖3），最后將這樣的推理經驗付諸其他活動的學習或問題的解決上。不難看出，這種補充教學環節的凸顯式教學，在數量依次乘10或翻倍的過程中，學生可以根據數量變化準確地推算出高度的變化，減輕了推算的難度，積累了推理經驗。在聯系實際判斷問題時，學生需要根據推算結果進行正確的判斷，大大豐富了學生解決問題的方法。簡化數量的過程，其實也是凸顯核心數據的過程，是提升學生推理能力的過程。

（圖3）

總之，數學起點型核心知識的教學應該著力于學生的知識生長、數學理解甚至素養形成而展開。教師通過采用凸顯式教學方式來開放教學時空、增設教學環節、拉長教學過程等，有助于學生在掌握起點型核心知識的基礎上，真正實現知識生長、思維進階、能力發展和素養提升。