某礦山的充填配合比及流變特性研究

周山山,姚秋萍,虞云林,楊八九

(1.云錫股份有限公司大屯錫礦, 云南 個舊市 661000;2.攀鋼礦業公司礦業設計研究院, 四川 攀枝花市 617000;3.云南亞融礦業科技有限公司, 云南 昆明 650093)

膏體充填是國內近幾年發展較為迅速的一種充填技術,因其具有良好的穩定性、流動性、可泵性和節能環保等眾多優點而備受關注[1]。一般情況下,膏體是以選廠尾砂為惰性骨料,摻和膠凝材料,再加上其他一些粗骨料,按照一定的配比混合,攪拌而成的一種膏狀漿體。本文主要利用流變儀確定充填料漿的流變學參數,確定適合的充填料漿質量濃度范圍,分析充填料漿的管道輸送沿程阻力損失[2],為礦山的充填料漿制備及輸送工藝的后續工作提供基礎數據,同時也為類似礦山的尾砂充填工藝流程提供借鑒。

1 礦山概況

某礦山為多金屬復合露天礦,區域上地勢屬西高東低,相對高差922～2122 m,屬深切割的高中山地貌。采礦方案采用露天與地下聯合開采的方式,初期為單一露天開采,露天開采末期建成坑采系統,露采結束后為單一地下開采。為保證礦山生產能力,地下開采需要多中段同時開采,此外為保證露天邊坡穩定,采空區必須充填。結合礦體開采技術條件,確定地下開采的采礦方法為上向進路式分層充填法,分兩步驟間隔回采:第一步驟采用膠結充填;第二步驟回采用非膠結充填,膠結料鋪面[3]。

2 工藝流程

通過現場調研,結合管道長度、陽光照射時長、場地大小、人員施工及挖掘機施工便利情況等因素,綜合考慮選定礦區內一處空曠場地作為取樣場地,其施工步驟如下。

(1)確定場地面積及施工。基于試驗所需的干尾砂、各種損失率以及試驗可能出現的失敗率,得出大概需要的干尾砂量,按尾砂與水的大概比重推算出需要挖的蓄砂坑(見圖1)。

圖1 施工坑底

(2)接管以及放漿。管口的一端綁在泵送機的接口處,另一端放進鋪好塑料布的坑底。

(3)鋪漿和翻曬。待到漿液靜置24 h后,用桶把坑底的砂漿盛到在鋪好的塑料上(見圖2)。

圖2 翻曬

(4)搬運和碾碎。經過翻曬,將干結成塊的砂漿碾壓成粉。

(5)裝袋及裝車。尾砂塊碾壓完成之后開始裝袋,運輸途中需防止尾砂遺漏。

(6)收尾工作。裝車結束后,進行清掃工作。

(7)混合均勻及烘干處理。試樣運回后經重新翻曬及人工混合均勻后,運至實驗室用烘箱分批烘干后重新裝袋。

3 尾砂粒度分析

為使試驗數據更加準確,本次試驗分兩次做,每次分成3組,最后求其所占比例平均值。第一次試驗取烘干試樣200 g,150 g,150 g,第二次烘干試樣每組分別取55 g。試驗步驟為:將500目篩放入盆中讓水浸泡,然后用小勺向200目篩中加入尾砂樣品,振動篩子讓水流沖洗尾砂,當第一個盆中砂樣濃度較高時,換至第二個盆中繼續沖洗,依次直至盆中水色清澈為止。試驗數據見表1。由表1可知,-100目(149 μm以下)尾砂的平均占比達96.57%,-200目(74μm以下)尾砂的平均占比達86.8%,-500目(30μm以下)尾砂的平均占比達55.62%。可知該礦尾砂相對較細,會對全尾砂的濃密脫水及充填體強度帶來一定的影響。

表1 水洗法試驗數據

4 充填料漿流變參數測試

4.1 測試所用流變模型

大量研究證明,全尾砂充填漿體的流變特性復雜,在層流狀態下,它是一種典型的非牛頓體,一般為屈服偽塑性體,具有屈服應力。用于漿體的動態流變模型有兩參數的Bingham模型、Casson模型、Power Law模型和3參數的Herschel-Bulkley模型等[4]。通常在充填料漿流變學參數研究中采用Bingham模型進行分析時較為貼近實際。

Herschel-Bulkley模型通式如下:

式中,τ為剪切應力,Pa;μ為表觀黏度,Pa·s;τ0為動態屈服應力,Pa;K為稠度系數,Pa·s;n為流態性能指數,n＜1。γ為剪切速率,s-1。當τ0=0,n=1為牛頓流體模型;τ0=0,n＜1為冪律體;當τ0＞0,n＜1時為屈服偽塑性體;當τ0＞0,n=1時為賓漢塑性體[5]。

4.2 充填料漿最佳濃度范圍分析

采用適用于對懸浮體和剛性膏體測量的RST Rheometer儀器通過流變學參數分析,結合尾砂粒級分析結果,初步確定充填料漿質量濃度試驗值分別為64%、66%、68%、70%、72%。由于分析數據較多,在此僅展示料漿質量濃度64%～72%的流變曲線,如圖3所示。從圖3可以看出,隨著質量濃度的增大,料漿在不同剪切速率下的剪切應力也隨之增大,當質量濃度超過68%時,剪切應力增幅較大。

圖3 不同質量濃度時充填料漿流變曲線

分別對上述5種料漿質量濃度的全尾砂料漿流變模型進行了擬合分析。通過回歸分析得到料漿質量濃度分別為64%、66%、68%、70%、72%時的屈服應力分別為3.74 Pa,12.35 Pa,28.44 Pa,57.41 Pa,130.24 Pa。回歸復相關系數達到0.9以上,說明采用3參數的H-B模型擬合得到的數據較為準確,料漿質量濃度與料漿屈服應力變化關系如圖4所示。

圖4 料漿質量濃度與料漿屈服應力變化關系

由圖4可以看出,隨著質量濃度的增大全尾砂料漿的屈服應力也相應增加。由圖4可知,該礦山全尾砂漿的屈服應力變化臨界范圍在68%～70%。因此,在未添加水泥的情況下,在68%～70%范圍內的充填料漿質量濃度可確保充填強度,保證順利輸送。

4.3 膠結充填料漿流變參數分析

考慮到充填過程中需要添加水泥,添加水泥后充填料漿屈服應力會相應增大。故,在試驗中主要分析了質量濃度分別為66%、67%、68%,灰砂比分別為1∶4,1∶8,1∶12時的流變參數。根據試驗數據回歸出相應的流變方程,并結合輸送管徑及流速對不同配比時的沿程阻力、管壁切應力進行分析[6]。流變模型回歸分析結果見表2。

從回歸結果來看:隨著料漿質量濃度增加,料漿屈服應力增大;在同等質量濃度條件下,隨著灰砂比增大料漿屈服應力增大,其中料漿質量濃度為66%、灰砂比為1∶12時的充填料漿屈服應力最小,為14.48 Pa,料漿質量濃度為68%、灰砂比為1∶4時的充填料漿屈服應力最大,為48.5 Pa。

4.4 沿程阻力損失計算分析

輸送管道的沿程阻力損失是指單位長度管道的壓力差,其大小反映了管道輸送的難易程度。此外,沿程阻力損失的確定對評價輸送系統的優劣性具有重要作用[7]。以賓漢塑性體模型的流變參數計算公式為原型,在基于表2得到的流變試驗結果基礎上,計算了充填料漿在不同工況輸送時沿程阻力情況。合理的充填料漿配比選取了7組,料漿質量濃度分別為66%、67%、68%,灰砂比分別為1∶4,1∶8,1∶12。計算時分別考慮了管徑為100 mm,150 mm,200 mm,流速分別為0.6 m/s,0.8 m/s,1.0 m/s,1.2 m/s,2.0 m/s時充填料漿輸送情況。

計算得出:隨著管徑的增大,沿程阻力不斷減小;隨著流速的增大,沿程阻力不斷增大。充填料漿質量濃度為68%、灰砂比1∶4時沿程阻力最大,在管徑為100 mm,流速分別為0.6 m/s,0.8 m/s,1.0 m/s,1.2 m/s,2.0 m/s時對應的沿程阻力分別為2952.35 Pa/m,3074.24 Pa/m,3196.14 Pa/m,3318.03 Pa/m,3805.61 Pa/m。充填料漿質量濃度為66%、灰砂比1∶12時沿程阻力在試驗范圍內最小,在管徑為200 mm,流速分別為0.6 m/s,0.8 m/s,1.0 m/s,1.2 m/s,2.0 m/s時對應的沿程阻力分別為484.62 Pa/m,517.45 Pa/m,550.28 Pa/m,583.11 Pa/m,714.42 Pa/m。

阻力損失分析時,賓漢塑性體模型的流變參數計算公式如下:

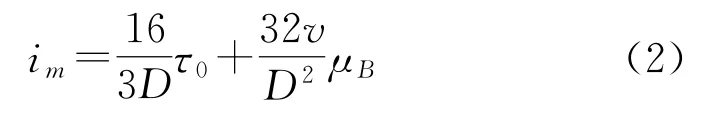
式中,i m為沿程阻力損失,Pa/m;τ0為漿體屈服應力,Pa;v為流速,m/s;D為管徑,m;μB為漿體塑性黏度,Pa·s。

4.5 管壁切應力計算分析

管壁切應力的大小反映了管道磨損率的大小,管壁切應力過大會導致管道磨損程度加大[8]。在基于表3得到的流變試驗結果的基礎上,以賓漢塑性體模型為原型,計算了充填料漿在不同工況輸送時管壁切應力情況。充填料漿配比為7組,料漿質量濃度分別為66%、67%、68%,灰砂比分別為1∶4,1∶8,1∶12。計算時分別考慮了管徑為100 mm,150 mm,200 mm,流速分別為0.6 m/s,0.8 m/s,1.0 m/s,1.2 m/s,2.0 m/s料漿輸送情況。

表3 不同配比流變擬合回歸試驗結果(賓漢塑性流體)

計算得出:隨著管徑的增大,管壁切應力不斷減小;隨著流速的增大,管壁切應力不斷增大。這與沿程阻力得到的變化規律一致[9]。充填料漿質量濃度為68%、灰砂比1∶4時管壁切應力最大,在管徑為100 mm,流速分別為0.6 m/s,0.8 m/s,1.0 m/s,1.2 m/s,2.0 m/s時對應的管壁切應力分別為73.81 Pa,76.86 Pa,79.90 Pa,82.95 Pa,95.14 Pa。

充填料漿質量濃度為66%、灰砂比1∶12時管壁切應力在試驗范圍內最小,在管徑為200 mm,流速分別為0.6 m/s,0.8 m/s,1.0 m/s,1.2 m/s,2.0 m/s時對應的管壁切應力分別為24.23 Pa,25.87 Pa,27.51 Pa,29.16 Pa,35.72 Pa。

切應力分析時,賓漢塑性體模型的流變參數計算公式如下:

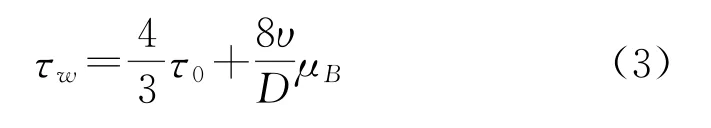
式中,τw為管壁處切應力,Pa;υ為漿體的平均流速,m/s。

5 結論

(1)通過水洗試驗得出,該礦山礦尾砂相對較細,會對全尾砂的濃密脫水及充填體強度帶來一定的影響。

(2)在全尾砂料漿(未添加水泥)情況下,隨著料漿質量濃度的增大全尾砂料漿的屈服應力也相應增加,全尾砂漿的屈服應力變化臨界范圍為68%～70%,未添加水泥時,建議充填料漿質量濃度位于此區間范圍。

(3)開展了料漿質量濃度66%、67%、68%,灰砂比1∶4,1∶8,1∶12充填料流變參數試驗,得到不同配合比料漿的流變模型、屈服應力,計算出沿程阻力損失、管壁切應力等參數。