基于事件觸發機制的分布時滯離散切換LPV系統H∞濾波器和控制器同步設計

李艷輝,張國旭, 毛 帥

( 1.東北石油大學 環渤海能源研究院，河北 秦皇島 066004; 2.東北石油大學 電氣信息工程學院，黑龍江 大慶 163318 )

0 引言

切換線性參數變化(LPV)系統是描述一類多模態切換、多非線性和時變特性的復雜實際系統，如飛行器控制系統[1]和工業生產設備控制系統等[2]。關于切換LPV系統研究方面，黃金杰等[3]提出一種基于平穩切換策略的LPV系統狀態反饋控制器設計方案，抑制子系統切換產生的瞬態響應。HE X等[4]研究一類離散切換LPV系統，得到滿足魯棒穩定性和H∞性能的充分條件。關于濾波器和控制器設計方面，ZHAO P等[5]研究平均駐留時間(ADT)切換下的狀態反饋控制器設計；WANG H等[6]研究干擾頻率受系統參數影響的切換LPV系統的濾波器設計。在實際控制系統中存在不可測的狀態變量，可能對系統的性能造成影響，因此將濾波器和控制器同步設計具有重要意義。

隨工業生產過程中網絡控制系統的應用，出現時滯問題[7]。ZHU K等[8]采用一種時滯無關的Lyapunov泛函，研究無時滯切換LPV系統，給出濾波器的求解方法。在實際工業控制系統中，時滯現象對系統性能造成嚴重影響[9]，數據在網絡傳輸過程中也存在傳輸時延等現象[10]。對于時滯切換LPV系統，DONG Y L等[11]構造時滯依賴的Lyapunov函數方法，研究非線性時滯切換系統的鎮定問題。基于模態依賴切換策略，LI Y H等[12-13]研究時滯切換LPV系統的H∞濾波問題，分析切換線性變參數系統的定階濾波問題，建立切換LPV系統的時延相關性能準則。分布時滯普遍存在于壓力進料和反應堆燃燒過程等系統[14]，可以準確反映事物本質特點[15]。因此，有必要研究具有分布時滯的切換LPV系統。

隨復雜系統的出現，包括油氣藏等行業技術和方法創新[16-17]，提高網絡資源利用率、保證系統穩定成為研究重點。傳統時間觸發機制將采樣信號全部傳輸至網絡，容易造成大量冗余信號[18]。采用事件觸發機制的網絡數據傳輸方式，可以有效利用網絡資源。為減少網絡帶寬使用，GU Y等[19]研究事件觸發機制下有限頻率規格的離散利普希茨非線性系統，設計故障檢測濾波器。ZHU C等[20]提出一種與觸發閾值系數相關的事件觸發狀態估計器，通過調整閾值平衡傳輸速率和估計器性能之間關系，有效減弱噪聲相關性和數據包丟失的影響。對于事件觸發機制下的切換LPV系統，QI J等[21]研究異步切換LPV系統的濾波問題，構造采樣時延相關參數化濾波誤差切換系統，設計有效濾波器。ZHU K W等[22]提出依賴于狀態和參數的兩種事件觸發方案，在滿足系統指數穩定的前提下，給出控制器的參數化求解方法，將控制器應用于航空發動機的切換LPV模型，取得較好的控制效果。

網絡控制系統存在網絡傳輸帶寬有限、系統狀態不可測及時延的現象。對于具有分布時滯的離散切換LPV系統，采用ADT方法，結合參數依賴切換律，提出H∞濾波器和依賴于濾波器狀態的控制器同步設計方案，引入兩個相互獨立的事件觸發條件，選擇在不同切換模態下傳輸信號，在切換律和控制器作用下，解決離散切換LPV系統的H∞濾波問題，采用LMI方法和凸優化算法求解濾波器和控制器參數。結合實例數值模擬，驗證事件觸發機制下濾波器和控制器同步設計方案有效且節約網絡資源。

1 問題描述

考慮分布時滯的離散切換LPV系統[23]：

(1)

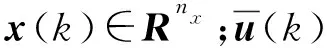
設計濾波器和依賴于濾波器狀態的控制器：

(2)

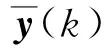
為了節約網絡資源，引入事件觸發策略，設定兩個相互獨立的事件觸發條件：

(3)

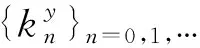
注1為了節約網絡資源，提高網絡傳輸的效率，對于濾波器和控制器分別設計兩個相互獨立的事件觸發條件，事件觸發閾值δ1和δ2分別決定測量輸出信號和控制輸入信號在網絡中的傳輸效率，閾值越大，傳輸的數據越少。

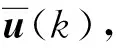
(4)

注2在實際網絡環境下，系統的測量輸出信號在數據傳輸過程中存在時延的現象，濾波器實際輸入為式(4)。由于控制器設計依賴于濾波器狀態，因此不考慮網絡時延對控制器的影響。

(5)

式中：

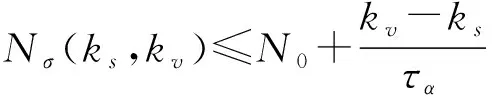
引理1[25]存在任意正實矩陣Mi和常數μm≥0(m=1,2,…)，滿足不等式

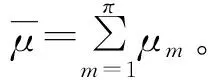
設計式(2)的濾波器和控制器，使增廣閉環系統式(5)指數穩定且滿足H∞性能，即在零初始條件下，對于任意非零ω(k)∈L2[0,∞)，存在常數γ1>0，γ2>0，滿足

2 切換LPV系統H∞性能分析

選取時滯依賴的Lyapunov泛函，給出增廣閉環系統指數穩定且滿足H∞性能指標的充分條件。

定理1給定標量μ≥1和0<θ<1，若存在常數γ1>0，γ2>0，則正定對稱矩陣Pi(ρk)>0，Qi>0和Mi>0，結合事件觸發閾值δ1、δ2，對于任意的i>j>0，不等式成立：

(6)

Pi(ρk)≤μPj(ρk),Qi≤μQj,Mi≤μMj。

(7)

切換信號的平均駐留時間滿足

(8)

證明選取Lyapunov函數

(9)

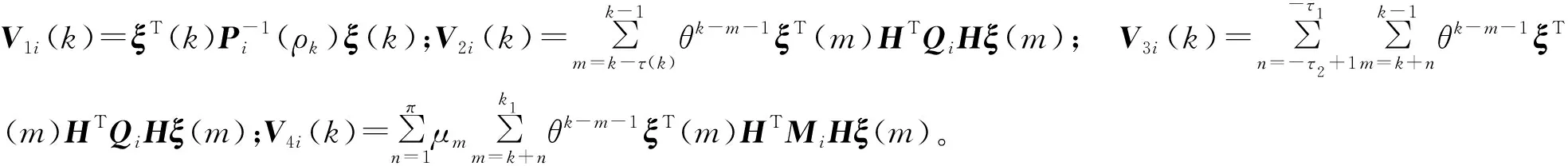
根據系統狀態求差分ΔVi(k)=Vi(k+1)-θVi(k)，可得：

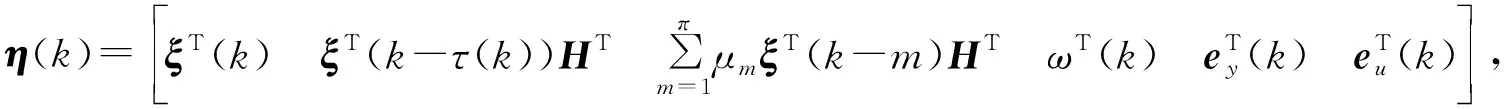
δ1yT(k)y(k)+δ2uT(k)u(k)=ηT(k)Φ1η(k)。

由Schur補引理有

(10)

由式(7)和式(9)可得Vi(k)≤μVj(k)，即Vσks(k)≤μVσks-1(k)。若式(6)成立，則式(10)成立，在[k0,k]上迭代得

(11)

根據定義1和式(8)、式(11)可得

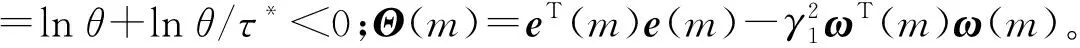
當ω(k)=0時，aσks>0，bσk0>0，aσks‖ξ(k)‖2≤Vσks(k)，Vσk0(k0)≤bσk0‖ξ(k0)‖2，則‖ξ(k)‖≤

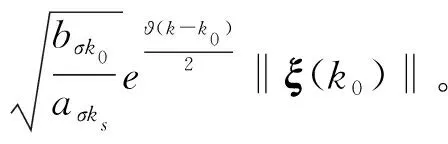
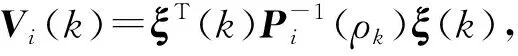
3 H∞濾波器和控制器設計

基于定理1，利用全等變換和變量替換，給出濾波器和控制器參數的求解方法。

(12)

(13)

Qi≤μQj,Mi≤μMj。

(14)

式(12-14)中：

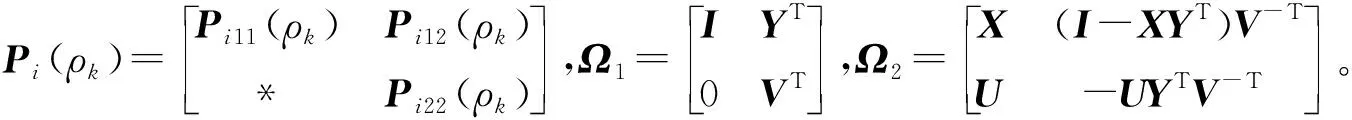
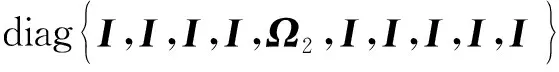
4 實例數值模擬

利用航空發動機的切換LPV模型驗證事件觸發機制下H∞濾波器和控制器同步設計方案的有效性。采用文獻[8]的建模方法，可得航空發動機控制系統的切換LPV模型：

控制系統模型參數及系統狀態變量的物理意義見表1。

表1 航空發動機控制系統模型參數及物理意義Table 1 The physical significance of model parameters and system state variables of aeroengine control system

應用曲線擬合方法[8]，將連續時間系統進行離散化處理，可得離散切換LPV模型：

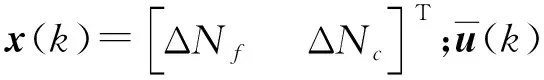
對于具有分布時滯的離散切換LPV系統式(1)，列出系統參數矩陣：

子系統1

子系統2

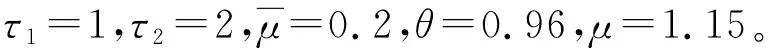
濾波器和控制器性能指標分別為γ1=1.164 0，γ2=1.399 0。兩個事件觸發閾值分別為δ1=0.094 4，δ2=0.500 0。

為了驗證選取的時滯相關Lyapunov泛函是否使系統具有更低的保守性，對比兩種不同Lyapunov函數方法下求解的最優H∞干擾抑制水平：采用時滯相關Lyapunov函數方法時，γ1為1.164 0，γ2為1.399 0；采用時滯無關Lyapunov函數方法時，γ1為1.320 2，γ2為1.542 5。由此可知，時滯相關Lyapunov函數方法在一定程度上降低系統的保守性。

根據濾波器參數矩陣和控制器增益矩陣進行數值模擬，驗證離散切換LPV系統H∞濾波器和控制器同步設計方案的有效性。控制器和濾波器作用下，分布時滯離散切換LPV系統狀態及估計誤差見圖1-2。由圖1-2可以看出，設計的控制器能起鎮定原系統狀態的作用，濾波器也能較好估計原系統狀態。

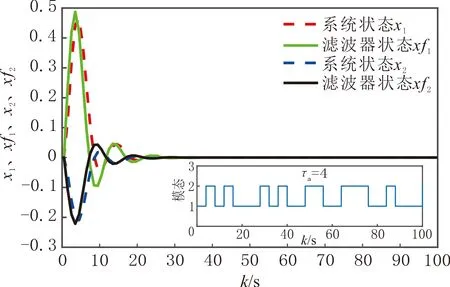
圖1 閉環控制系統狀態和濾波器狀態Fig.1 Closed-loop control system status and filter status

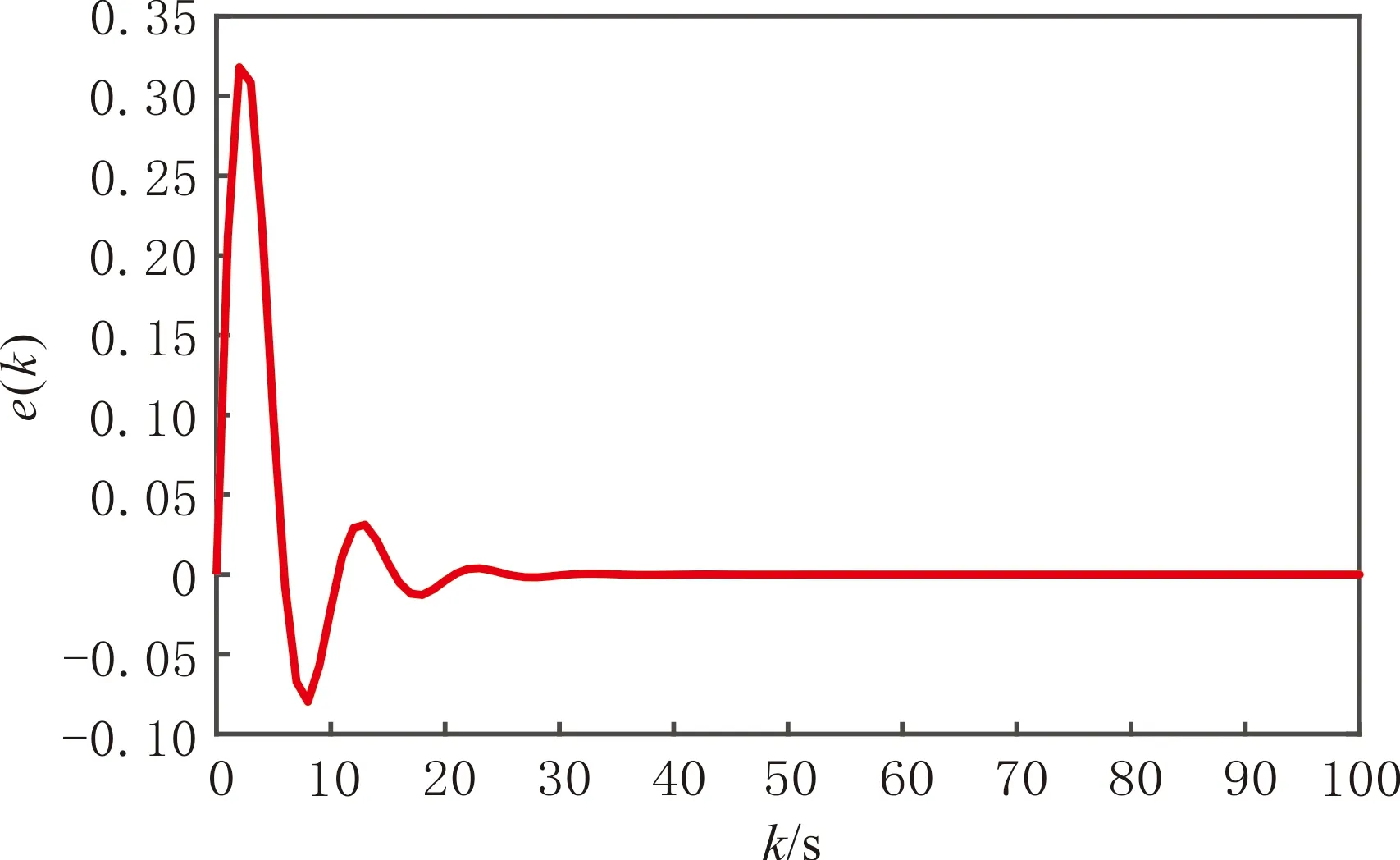
圖2 閉環控制系統估計誤差Fig.2 Closed-loop control system systematic estimation errors

事件觸發機制下測量輸出數據傳輸時刻和傳輸間隔見圖3。由圖3可知，數值模擬時間為100 s，事件觸發機制下只有70個數據被成功發送，傳輸率為70%，而傳統的時間觸發機制需要將采樣數據全部發送給濾波器。事件觸發機制下控制數據傳輸時刻和傳輸間隔見圖4。由圖4可知，在事件觸發機制下只有41個數據被成功發送，傳輸率為41%，相較于傳統的時間觸發機制，節約大量通信資源。事件觸發機制下離散切換LPV系統濾波器和控制器同步設計方案，既節省網絡資源，又保證性能指標。

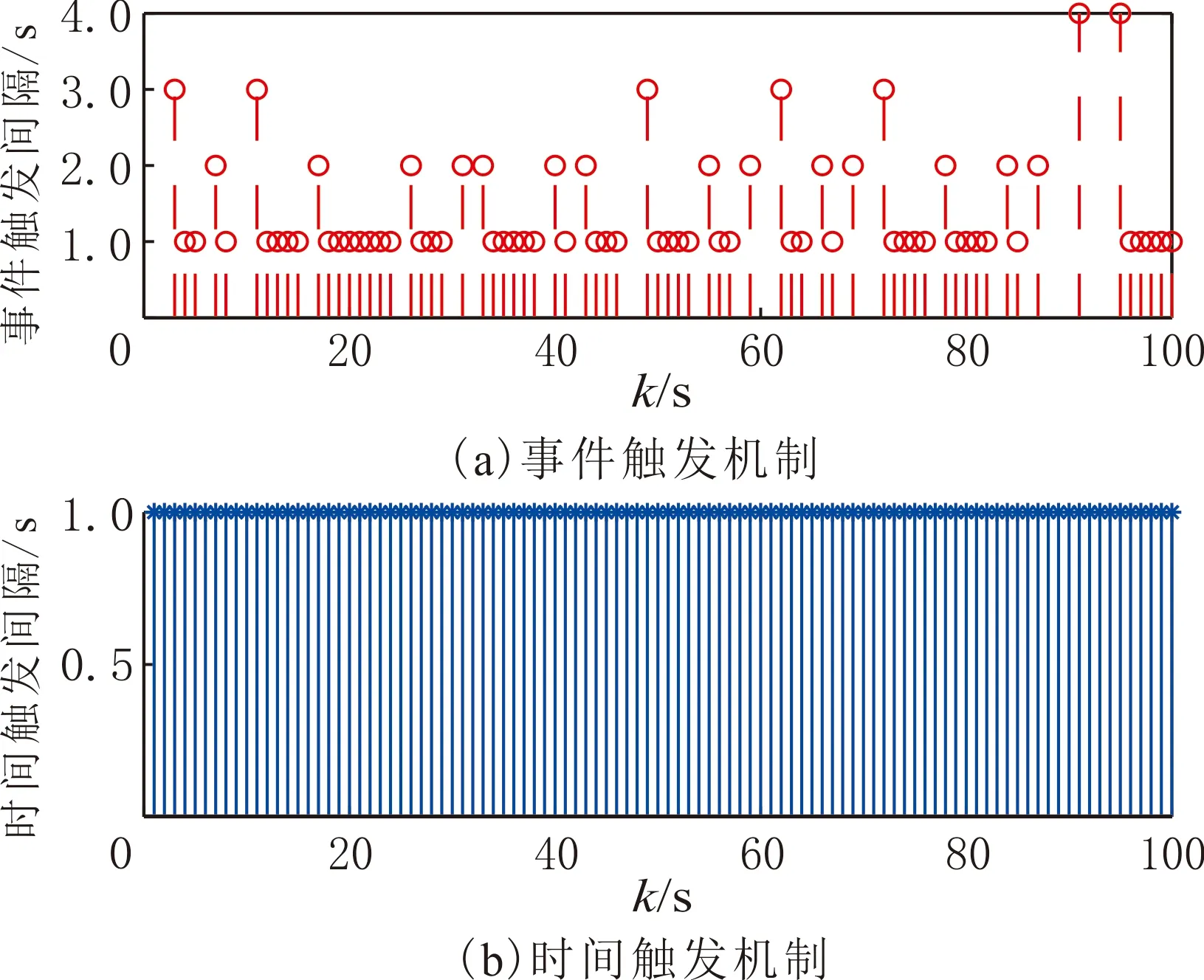
圖3 事件觸發機制下測量輸出數據傳輸時間和間隔Fig.3 Time and interval of measurement data transmission under event-triggered mechanism

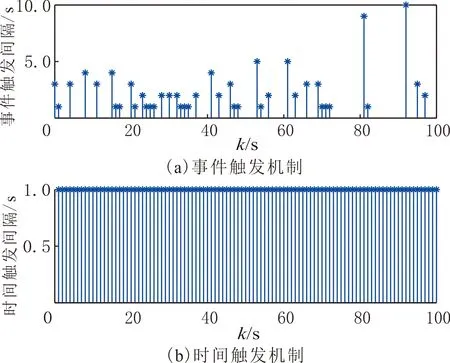
圖4 事件觸發機制下控制器輸出數據傳輸時間和間隔Fig.4 Time and interval of controller output data transmission under event-triggered mechanism

5 結論

(1)對于事件觸發機制下具有分布時滯的離散切換LPV系統，提出一種H∞濾波器和控制器同步設計方案，可以滿足H∞性能指標，使控制器在系統狀態不完全可測的情況下，能夠鎮定原系統狀態，提升系統性能。

(2)設計兩個相互獨立的事件觸發條件，有效減少網絡帶寬占用，節約網絡資源，時滯相關Lyapunov泛函可以降低系統的保守性，實例數值模擬驗證設計方案的有效性。