等離子體中渦旋光束自聚焦與成絲現象的模擬研究*

范海玲 郭志堅 李明強 卓紅斌

(深圳技術大學工程物理學院,深圳 518118)

渦旋光束在低密度等離子體傳輸過程中出現的非線性物理效應與光子攜帶的軌道角動量 (拓撲荷) 存在密切關聯.基于亥姆霍茲方程理論獲得描述渦旋光束傳輸的旁軸近似方程,解析求出渦旋光束在低密度等離子體中傳輸的自聚焦臨界功率表達式.利用分步傅里葉數值方法,針對不同參數條件下渦旋光束的自聚焦和成絲現象進行了模擬分析.研究結果表明,渦旋光束的拓撲荷數決定了自聚焦臨界功率大小.渦旋光束發生成絲不穩定性現象的功率閾值和最大成絲數目與拓撲荷數存在密切關聯.

1 引 言

強激光自聚焦以及成絲不穩定性現象是激光等離子體物理研究的重要內容[1].在間接驅動激光核聚變點火實驗中,多路激光束在黑腔等離子體中傳輸,極易觸發自聚焦和成絲不穩定現象[2].該現象直接破壞激光束強度分布的均勻性,進而影響激光-X 射線轉化效率和X 射線輻照均勻性;同時還可能觸發各類參量不穩定性,導致超熱電子的產生,間接影響內爆靶丸的壓縮效率.在相對論強場物理范疇,自聚焦效應能夠導致局部光強大幅增強,產生傳輸通道電子排空以及形成穩定的激光傳輸通道[3].伴隨著激光自聚焦和成絲過程,還可能出現自生磁場產生以及高能電子加速等復雜物理現象.激光自聚焦以及成絲不穩定性現象的大量研究工作主要集中在理想高斯光束的參數條件下.近期,渦旋光束作為一種光強分布為環狀,波前相位為螺旋狀的光束,其在傳統介質中傳輸發生的非線性效應與光子攜帶的軌道角動量(拓撲荷)存在密切關聯,引起了研究人員的廣泛關注.Kruglov 等[4]研究發現渦旋光束自聚焦臨界功率與拓撲荷數呈正相關關系,Feit 和Fleck[5]通過數值模擬發現攜帶軌道角動量的渦旋光束能穩定傳輸更長的距離,同時渦旋光束在自聚焦后會出現成絲和光束破裂現象.Vuong 等[6]通過實驗和數值分析表明渦旋光束拓撲荷數以及初始功率的增大都會使光束成絲數目變多.近期,利用渦旋激光束開展激光粒子加速[7]、高次諧波產生[8]、以及利用受激拉曼放大實現高功率渦旋激光束[9]等相關研究成為激光等離子體物理研究的熱點方向.

本文針對高功率渦旋光束在低密度等離子體傳輸過程中的自聚焦和成絲過程開展理論分析和數值計算研究.基于亥姆霍茲方程,理論推導出描述渦旋光束傳輸的旁軸近似方程,解析獲得渦旋光束的自聚焦臨界功率表達式.在此基礎上,利用分步傅里葉數值方法求解波動方程,并對不同參數條件下渦旋光束在低密度等離子體中傳輸特性進行了分析計算.模擬結果顯示,渦旋光束的拓撲荷數越大,對應的自聚焦臨界功率越大.當激光初始功率足夠大時,渦旋光在自聚焦過程中會出現環狀結構破裂成絲的現象,其成絲數目與拓撲荷數呈現整數倍關系.隨著成絲不穩定性現象的不斷發展,渦旋光束成絲過程的后期能夠激勵產生更高階的調制不穩定性模式.在多重調制不穩定性模式共同作用下,渦旋光束會出現成絲結構強度分布的角向調制現象.

2 理論分析

考慮一束線極化渦旋激光束沿z方向在均勻等離子體中傳輸的物理過程.近似忽略各類激光散射等離子體不穩定過程,并假定激光場有質動力與等離子體空間電荷分離場達到熱平衡狀態,則描述激光電場傳播的標量亥姆霍茲方程形式如下[10,11]:

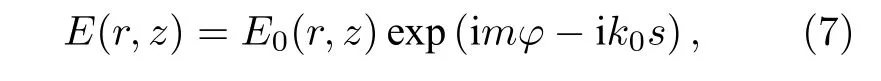
(10)式和(11)式具體描述了光束半徑縮放因子f和相位差ψ隨激光傳輸距離z的變化情況.這里,令f=1 且 d /dz=d2/dz2=0,表示光束半徑和振幅在傳輸過程中維持不變,由(10)式和(11)式即可得到光束傳輸的穩態解:

其中,λv為激光的真空波長.依據上述理論結果,對于給定的初始渦旋光束等離子體參數條件,如果入射功率大于臨界功率值Pc,則激光傳輸過程中光束半徑會逐漸減小,即發生自聚焦現象.當入射功率小于臨界功率值Pc,則激光傳輸過程中光束半徑會逐漸增大,即發生散焦現象.圖1 給出了n=0.05nc,0.1nc,0.15nc,0.2nc四組初始等離子體密度下自聚焦臨界功率隨拓撲荷數m變化的關系曲線,等離子體溫度設定為Te+Ti=3.5 keV.如圖1 所示,自聚焦臨界功率大小與拓撲荷數呈現正相關關系.同時,自聚焦臨界功率與初始等離子體密度呈反相關.初始等離子體密度越大,有質動力的作用下等離子體密度區域不均勻性會越強,從而導致局部區域內的折射率增大,進而使得激光更容易發生聚焦效應,自聚焦臨界功率值更小.

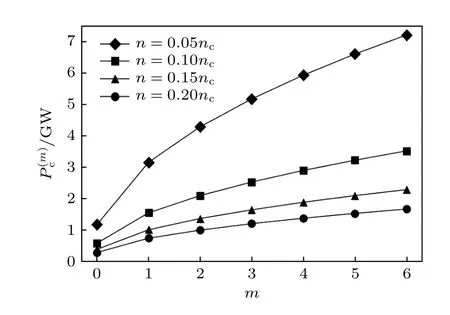
圖1 不同等離子體密度下的自聚焦臨界功率 與拓撲荷數m 的關系曲線Fig.1.The relationship between the critical power for selffocusing and the topological charge m at different plasma densities.

3 數值模擬方法

上述解析理論能夠較好地描述整體渦旋光束的傳輸和自聚焦行為,然而對于渦旋光束發生強自聚焦現象并可能導致成絲不穩定性的物理過程,必須借助數值模擬方法來精確求解亥姆霍茲方程.根據Feit 和Fleck[5,19]提出的數值模型,將(1)式改寫為如下形式:

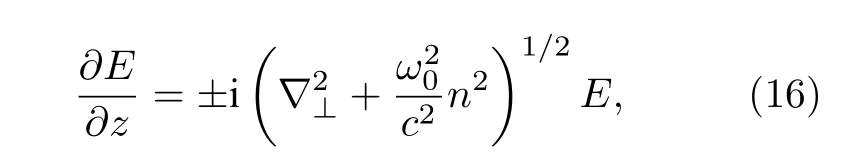
式中,

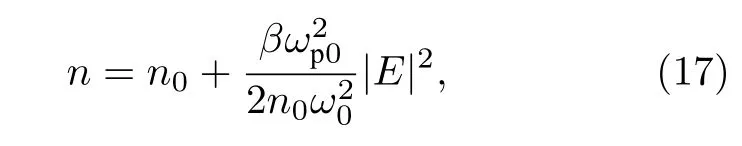
為非線性等離子體折射率[20],由線性折射率n0=和激光有質動力項 |E|2導致的非線性變化量組成.假定光束空間傳輸距離 Δz足夠小,且Δz內折射率變化可忽略,則(16)式解的形式可以表示為

代入(18)式,最終可以得到傅里葉電場振幅項的數值求解形式:

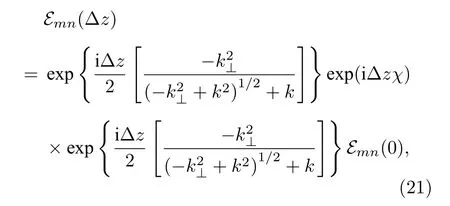
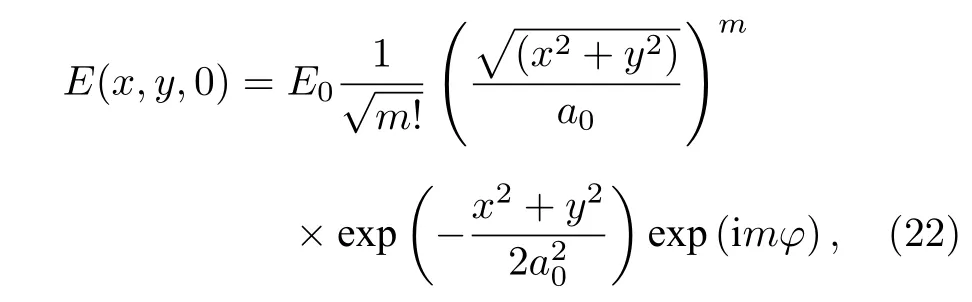
其中,E0是電場振幅,a0為初始光斑大小.由于渦旋光束存在相位奇點,用a0來描述渦旋光的光斑半徑是不合適的,這里采用橫向電場振幅最大值處的圓周半徑來描述渦旋光束的光斑尺寸.當m=0 時,上式退化為標準的高斯光束表達形式.

4 模擬結果分析與討論

依據(16)—(22)式,編寫完成三維激光傳輸模擬程序,并利用該程序模擬研究渦旋光束在低密度等離子體傳輸過程中的自聚焦和成絲現象.選擇模式作為入射渦旋光束,激光功率在—范圍內取值.具體模擬參數設定如下: 激光波長為λv=1 μm ,入射焦斑半徑為rm=20 μm,初始等離子體密度為 0.1nc,nc為等離子體電子臨界密度,等離子體溫度為Te+Ti=3.5 KeV,橫向空間網格劃分為 5 12×512,橫向網格大小為Δx=Δy=0.4λ,縱向傳輸步長為 Δz=4λ.模擬結果顯示,當入射激光功率遠小于時,渦旋光束的傳輸行為呈現散焦的狀態.當入射激光功率大于或等于時,渦旋光束傳輸出現自聚焦現象.

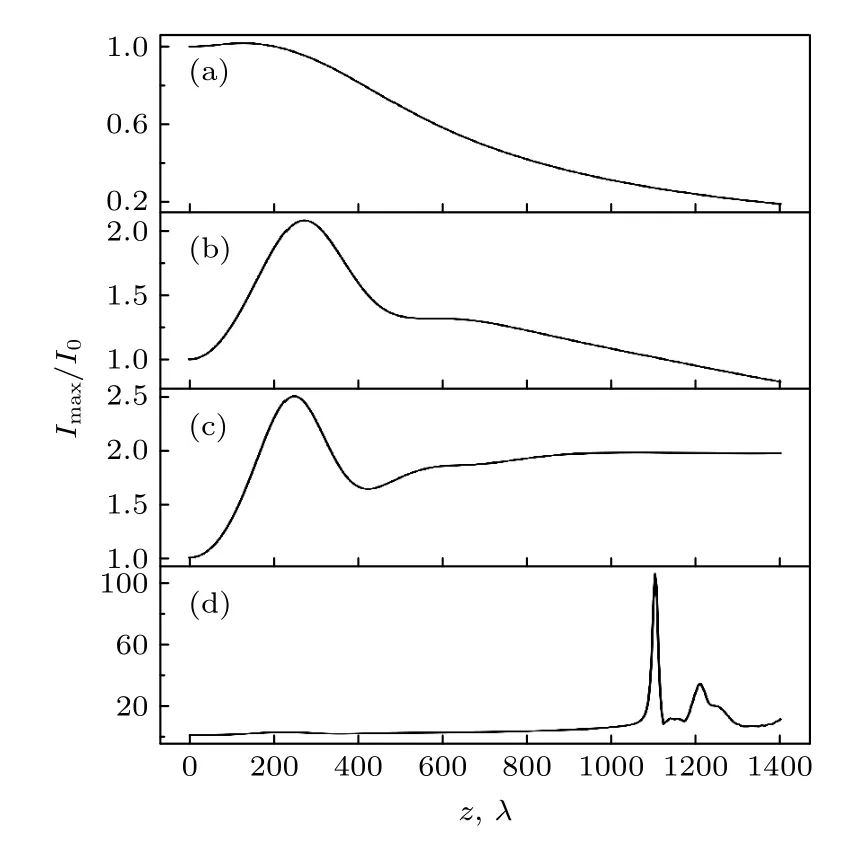
圖2 不同功率下渦旋光束峰值光強隨傳輸距離變化的模擬對比圖 (a) P=;(b) P=;(c)P=;(d)P=Fig.2.Normalized maximum intensity of vortex beams with different in put powers versus propagation distance for m=4:(a)P=;(b) P=;(c) P=;(d)P=.

圖3 不同功率下渦旋光束傳輸至不同位置的光強橫向分布圖 (a)—(c) P = ;(d)—(f) P = ;(g)—(i) P=Fig.3.Intensity distribution of vortex beams with different input powers at different positions: (a)–(c) P = ;(d)–(f) P =;(g)–(i) P = .The initial parameters are the same as in Fig.1.

Firth 和Skryabin[21]利用角向調制不穩定性理論模型對渦旋光束在非線性光學介質中的成絲現象給出了合理的解釋.研究表明,調制不穩定性最大增長模式和增長率由渦旋光束的入射功率和拓撲荷數m值來決定.對于各向同性的克爾介質,三階χ(3)非線性極化決定了引起的折射率變化,最大成絲數目與拓撲荷數必須滿足整數倍數關系.由前面的理論分析可知,等離子體折射率的非線性變化量表示為 Δn=(n ?n0)∝|E|2,同樣滿足上述非線性極化關系.圖4 中觀察到的模式渦旋光束的成絲數目恰好為拓撲荷數的2 倍,初步表明角向調制不穩定性理論模型同樣適用于超強渦旋光束在低密度高溫等離子體中成絲現象的解釋.

為進一步分析渦旋光束在等離子體中發生成絲的規律,給出了P=兩組參數下渦旋光束成絲現象的模擬結果,如圖5 所示.當P=,成絲數目增大到12 條,當P=,成絲數目增大到16 條.很顯然,隨著入射激光功率的進一步提升,渦旋光束的成絲數目出現了成倍數的增加,并且每次增加的成絲數目均為渦旋光束的拓撲荷數.接下來,改變渦旋光束的初始拓撲荷數,調整入射激光功率大小,進一步觀察渦旋光束的成絲數目的差異性.圖6 給出模、模渦旋光束成絲現象的模擬結果.當入射功率增大到時,模擬觀察到模的成絲現象,成絲數目為4 條,是拓撲荷數的2 倍.對于模而言,當入射功率達到時才開始發生自聚焦成絲現象,成絲數目為12 條,同樣為拓撲荷數的2 倍.很顯然,模擬發現的成絲規律與理論模型結果[21]以及文獻[22]報道的傳統光學介質的實驗結果十分符合,這表明等離子體作為非線性光學介質同樣具有良好的穩定性和可靠性.這里值得注意的是,隨著成絲不穩定性現象的不斷發展,我們發現模渦旋光束生成的成絲結構的強度分布會出現明顯的調制現象.如圖6(e)和圖6(f)的光強分布圖所示,模生成的12 條光絲可以根據強度差異分成3 組(圖中相同的數字對應細絲光強相同),每組包含4 條強度相同的光絲,同樣呈現角向周期分布特性.Firth 和 Skryabin[21]提出的一階線性微擾模型并不適用于這種強非線性物理現象解釋.這里,我們認為是渦旋光束成絲過程的后期,更高階的調制不穩定性模式被激勵起來.在多重調制不穩定性模式的共同作用下,形成了模擬中觀察到的成絲結構強度分布的角向調制現象.

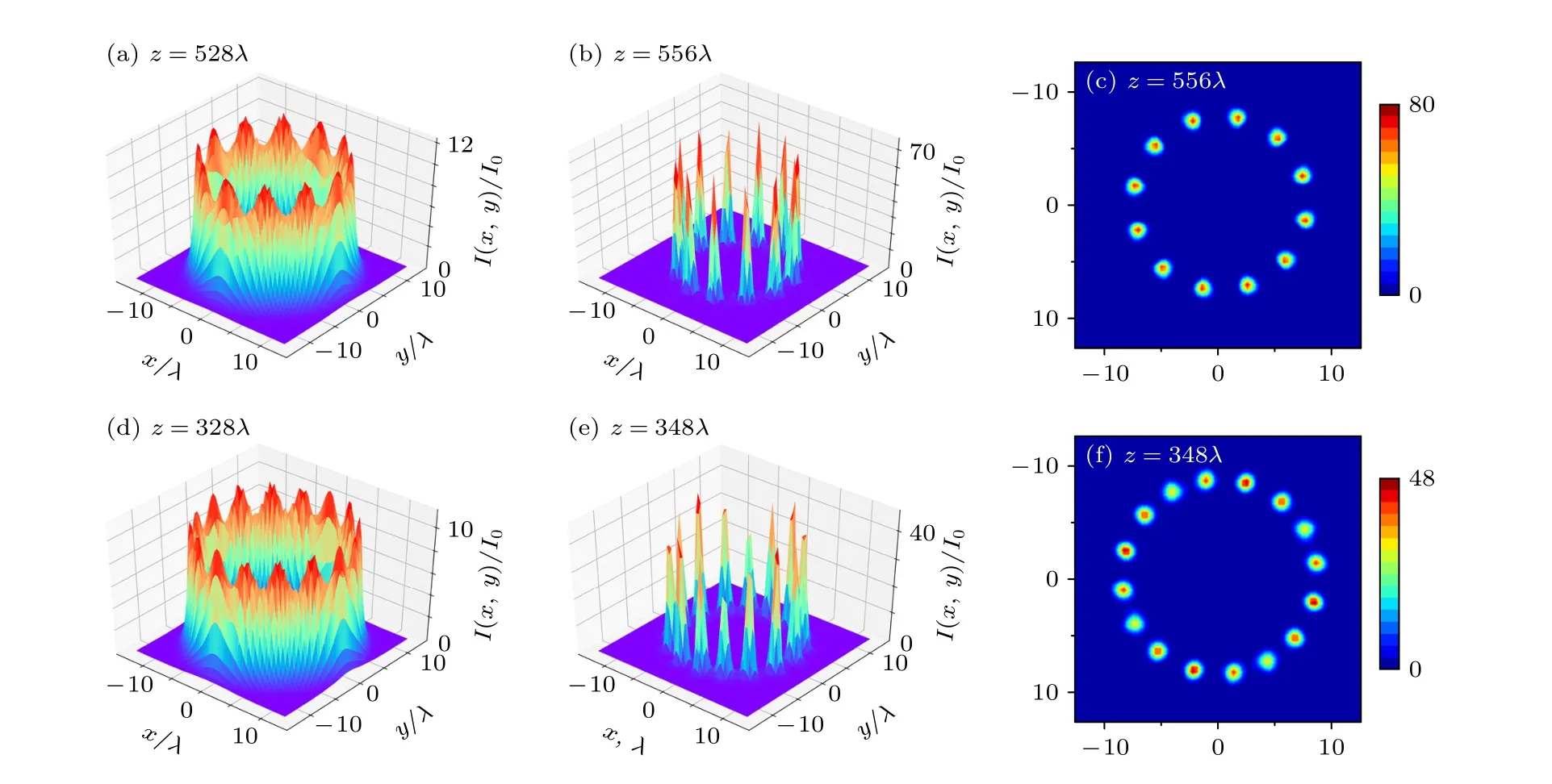
圖5 P =, 兩組參數下渦旋光束成絲現象的模擬結果 (a)—(c) P = ;(d)—(f)P=Fig.5.Filament formation of the vortex beams that has different high powers: (a)–(c) P = ;(d)–(f) P =,where m=4 are taken.

圖6 模、 模渦旋光束成絲現象的模擬結果對比圖 (a)—(c) m =2,P=;(d)—(f)m=6,P=Fig.6.Evolution of vortex beams with different values of the topological charge when the initial power is just enough to generate filaments: (a)–(c) m =2,P= ;(d)–(f) m =6,P=.

等離子體作為非線性光學媒介來實現短脈沖超強激光放大是目前國際上超強激光研制技術的熱點方向之一.依據文獻[23]提出的增益模型,利用等離子體受激拉曼散射放大機制獲得的最大增益光強由朗繆爾等離子體波破條件決定[23],理想峰值激光矢勢可表示為Amax≈(ωp0/ω0)3/2×105V,與等離子體密度成正相關關系.顯然,為提升激光增益,需要采用較高密度的等離子體作為媒介.然而,根據(22)式,較高的等離子體密度條件對應較低的自聚焦臨界功率閾值.這使得高斯激光束在放大過程中極易出現自聚焦和成絲不穩定性現象,并最終導致增益光強遠遠小于理論估算值.相較于理想高斯光束,相同功率、波長和等離子體參數條件下的渦旋光束具有更高的自聚焦和成絲不穩定性發生閾值,該特性有助于開展超強渦旋光束等離子體受激拉曼散射放大技術的實驗研究.選擇種子激光為模,泵浦激光維持為傳統高斯光束,激光波長均設定為 1 μm,等離子體電子密度為2.2×1020cm?3,則模的自聚焦閾值功率為普通高斯光束的5.1 倍(參考圖1 中的n= 0.2nc),明顯能夠抑制種子激光放大過程中可能出現的自聚焦和成絲現象,從而獲得理想的激光放大效果.利用三維粒子模擬程序開展LG 渦旋光束的等離子體受激拉曼散射放大機制的模擬研究將是我們下一步的研究工作.

5 結 論

本文主要研究了渦旋光束在低密度高溫等離子體中自聚焦和成絲物理現象.基于亥姆霍茲方程以及旁軸近似條件,推導出渦旋光束在等離子體中傳輸的穩態解,并得到了渦旋光自聚焦臨界功率表達式.利用分步傅里葉法的迭代計算方法,模擬得到了不同參數條件下渦旋光在低密度等離子體中傳輸的物理圖像.模擬結果顯示,拓撲荷數與渦旋光自聚焦臨界功率呈正相關關系,增加拓撲荷數可以有效抑制渦旋光束的自聚焦和成絲現象.當入射激光功率遠大于自聚焦臨界閾值,渦旋光束成絲數目與拓撲荷數呈現整數倍數關系.隨著成絲不穩定性現象的不斷發展,渦旋光束成絲過程的后期能夠激勵產生更高階的調制不穩定性模式.在多重調制不穩定性模式共同作用下,渦旋光束會出現成絲結構強度分布的角向調制現象.本文的研究結果表明: 相較于傳統的高斯光束,相同功率、波長和等離子體參數條件下的渦旋光束在等離子體中傳輸具有更高的自聚焦和成絲不穩定性發生閾值,該特性有助于開展超強渦旋光束等離子體受激拉曼散射放大技術的理論和實驗研究.