結合堆疊稀疏自編碼器與改進深度森林的竊電檢測方法
王耀聃 李紅嬌 詹清欽
(上海電力大學計算機科學與技術學院 上海 200090)
0 引 言
電能損耗中的非技術性損耗(Non-technical loss, NTL)主要是指交付和消費過程中被損耗但不能向終端用戶收費的電能,例如竊電和非法用電等異常用電行為帶來的損耗。智能電表的部署是智能電網解決竊電的有效形式之一。智能電表在電網中廣泛普及,使得用電數據的采集范圍得到了顯著提高,基于數據驅動的模式來檢測用戶竊電行為的潛力隨之增加[1]。通過減少電力盜竊可以降低單位供電成本,對于電力成本的長期管理至為關鍵。
目前,基于數據驅動的用戶竊電行為檢測方法主要有兩種。一種是直接利用分類模型完成正常用戶和異常用戶的識別,主要有神經網絡[2]、決策樹[3]和支持向量機[4]等。這些方法雖然取得了一定的效果但未注重用電數據特征的分析與選擇。用戶正常用電行為與竊電行為分別反映出相應的行為慣性,兩者之間存在著潛在的不明顯分類規律。僅靠分類模型進行判別,而未考慮特征提取會造成檢測精度不高,特別是對于較小數據集而言[1]。
第二種檢測方法結合特征提取與分類算法,通過構建用戶用電量數據特征集合,利用分類模型分析學習用電量數據特征集和用戶用電行為之間的映射關系,使用訓練得到的分類模型來預測用戶的用電行為屬性,達到對竊電行為的識別[5]。在特征提取方面,文獻[6]由用戶的日負荷曲線定義了4種度量指標,提取出13個特征變量。文獻[7]利用統計特征確定出各類特征指標,再利用主成分分析(Principal component analysis, PCA)提取用電數據特征。文獻[8]提出一種用電行為特征優選策略,通過對相關電力負荷指標(如日負荷率、峰谷系數等)的定量分析,實現特征集優化選擇。文獻[9]通過引入社群習慣建立了四個社群特征指標對用戶進行行為分析。在分類算法方面,文獻[10]從數據挖掘的角度,構建基于人工神經網絡的竊電風險等級模型,利用該模型對用戶行為等級進行分類。文獻[11]提出了一種社交蜘蛛優化的改進支持向量機參數調整與特征選擇模型用于竊電檢測。文獻[12]引入了欠完備自編碼器提取特征,隨后采用傳統BP算法對用戶用電行為分類,與淺層模型相比提高了特征的有效性,表明了自編碼器在特征提取中的潛力。但其采用的傳統BP神經網絡易陷入局部最小值。文獻[13]引入了深度森林(Deep forest, DF)[14]算法判斷用戶是否具有竊電傾向。DF具有參數設定少、對超參數設置不敏感、適用于小規模數據集等優點,由于用電數據集規模較小故將其用于竊電檢測工作上有一定的優勢。
以上研究雖然通過實驗論證了其優勢,但仍有改進的空間,原因在于:
(1) 特征有效性不高。以上特征提取方法均從電氣量統計變換的角度進行研究,依賴先驗知識,且模型為淺層模型,難以自動處理數據間的非線性復雜關系,尋找深度隱含特征。
(2) 分類算法未考慮樣本類別數量上的不平衡關系。在實際電網營銷系統中,正常用戶數量與竊電用戶數量具有明顯不平衡關系。所提方法并未考慮此因素,導致算法更加偏重樣本數量占多數類的正常用戶而忽略樣本數量較少的竊電用戶,最終整體檢測準確率虛高而少數竊電用戶的檢出率不高。
本文針對以上問題,結合上述自編碼器與深度森林的優勢,提出一種堆疊稀疏自編碼器(Stacked sparse autoencoder, SSAE)與基于海林格距離[15]的深度森林(Hellinger distance deep forest, HDDF) 相結合的竊電檢測模型。將整個檢測過程分為基于SSAE的用電量數據特征提取階段和基于HDDF的用戶用電行為分類檢測階段。將SSAE與HDDF結合,可看作是兩級數據處理和分析方法,SSAE提取的有用特征作為后續分類器的輸入,由于對原始用電量數據進行了再表征,強化了HDDF的分類表征學習能力,提高了模型的分類檢測精度。具有以下優勢:
(1) 相比于統計特征提取方法,深度模型SSAE的應用,可以以較少的數據維度實現用電量數據中有用特征的自動提取。同時,克服了普通自編碼器容易過擬合的缺陷,提高了特征數據的有效性。
(2) 將DF改進為HDDF,即DF結構中決策樹的分裂標準由Gini系數替換為對樣本類別數量分布不敏感的Hellinger distance度量方法,降低了數據集不平衡性對分類精度的影響,提高了竊電用戶的檢出率。
1 SSAE-HDDF模型構建
1.1 用電數據分析
竊電行為識別的關鍵之一在于提取用電數據的關鍵特征。竊電行為直觀上將導致異常的用電量示值。圖1顯示了兩種不同的異常用電數據類型。在圖1(a)中,該類竊電用戶全年出現低用電量情況較多,對應的竊電方式為高頻低量。在圖1(b)中,異常用戶前五個月幾乎沒有任何電量示數,這有可能是智能電表自身故障造成,但也有可能是人為操控電表使部分時期內電量示數遺失,對應竊電方式為階段連續竊電。

(a) 竊電類型1
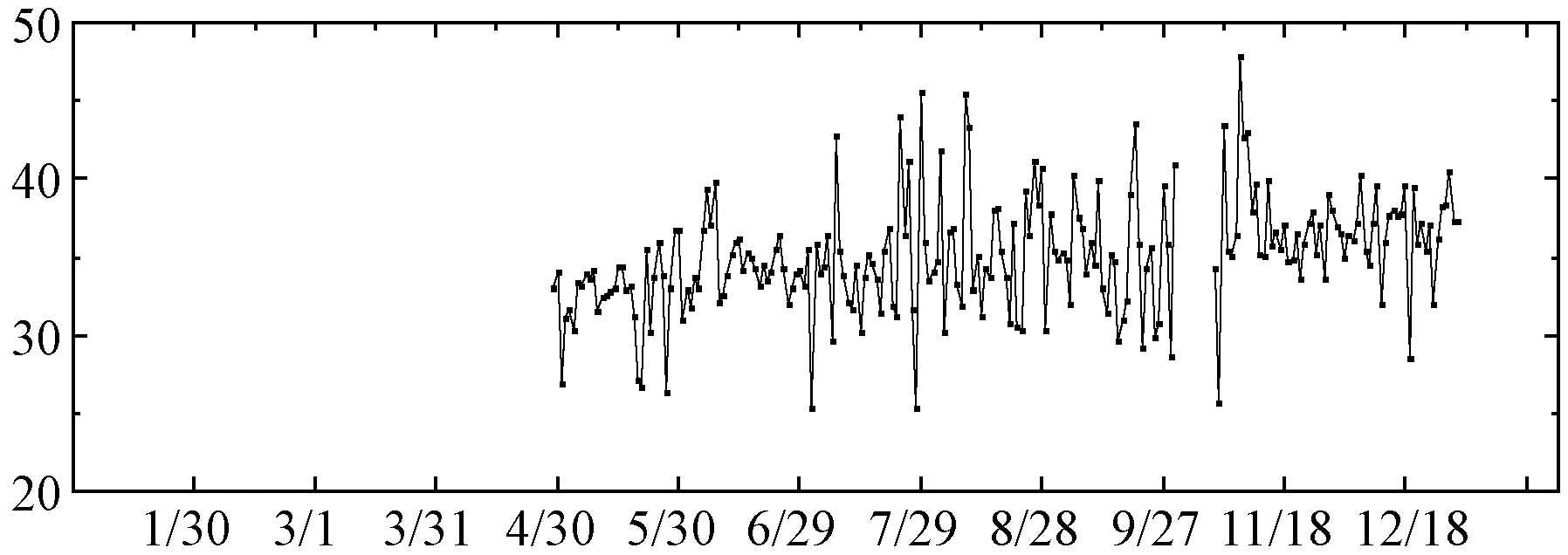
(b) 竊電類型2圖1 典型竊電類型
圖2以一個用戶為例,以周為單位繪制了9周(2個月)的用電量箱型圖。第一個箱子代表了9周中周一用電量數據,以此類推,第七個箱子表示周日用電量數據。如圖2(a)所示,正常用戶箱子長度均較短,其中周五最短,表示9周內周五的用電量相差不大,波動最小。通過上下四位數和中位數的間距也可以看出,整體每天的用電量分布較為對稱。相反地,在圖2(b)中,每個箱子的長度都比正常用戶的箱子長度長,這表明用電量數據較分散,即用電量波動較大。且竊電用戶的用電量分布呈較不對稱趨勢,在周一與周五中分別有一個離群點(異常值)。

(a) 正常用戶 (b) 竊電用戶圖2 正常/竊電用戶周用電量
通過對正常用戶和竊電用戶的用電量數據進行統計分析可以觀察到,竊電用戶的用電量數據呈以下特點:① 用電量波動程度較之正常用戶更為陡峭;② 用電量分布較不對稱,具有較少周期性或非周期性。然而,基于統計提取出的特征較為粗糙,電量數據間可能含有非線性相關性,手動提取特征并不能滿足需求,很難挖掘出用戶用電行為的深層規律。因此提出一種采用SSAE技術從用電量數據中自動挖掘其特征的方法。在SSAE中通過構建多層非線性變換網絡對原始用電數據進行建模,逐層學習更高級別的功能,以提取用電數據的高階抽象特征。
1.2 基于堆疊稀疏自編碼器的特征提取

SAE在普通自編碼器的基礎上,對隱藏層節點進行一些稀疏性的限制(如圖3所示),可從隱藏層H={h1,h2,…,hi}中得到比原始用電數據更好的特征描述。本文使用加入KL散度懲罰項的損失函數對用電數據進行稀疏性約束,引入了正則化參數λ防止自編碼器出現過擬合問題。稀疏自編碼的整體代價函數可表示為式(1),其中nl表示網絡層數,Sl表示l層神經元數量。
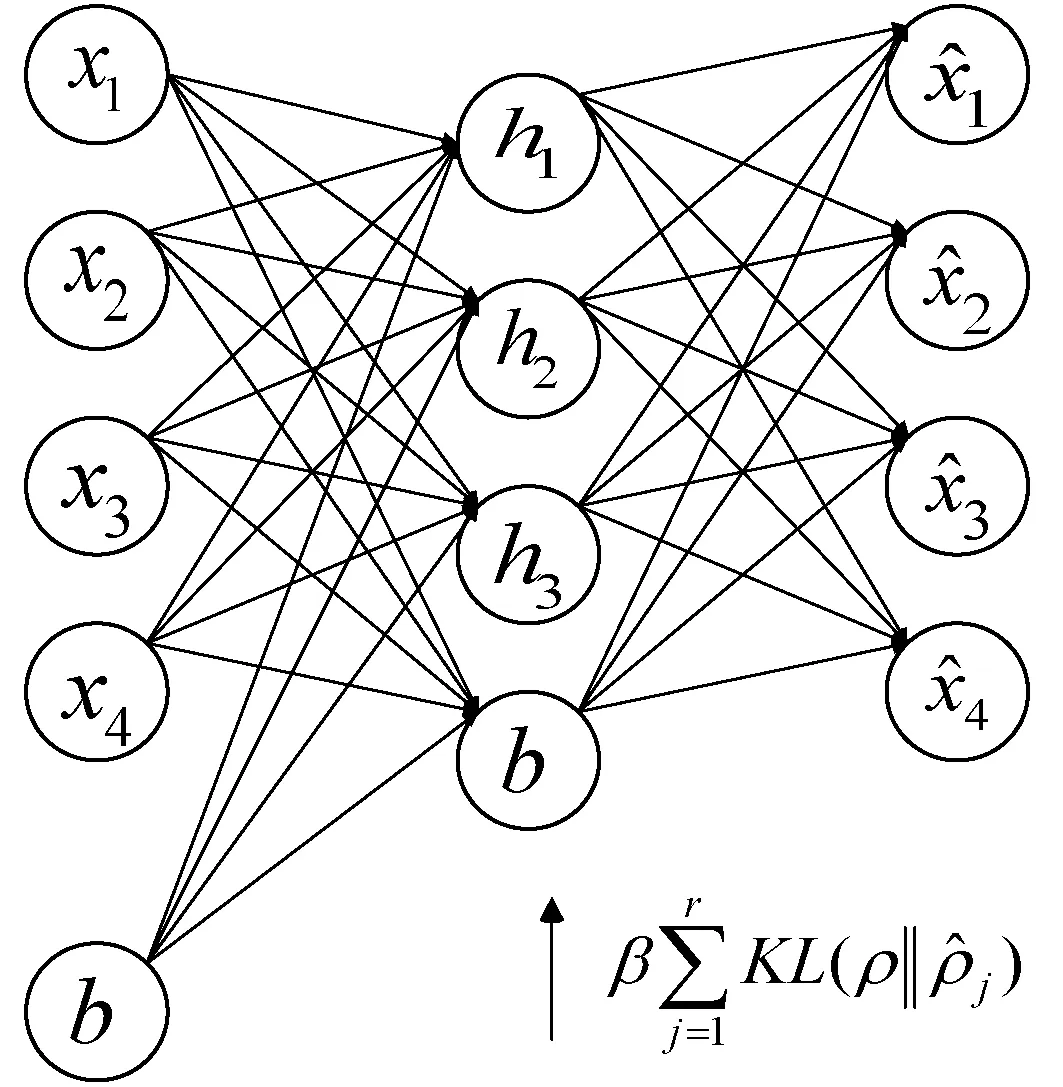
圖3 稀疏自編碼器結構

(1)
(2)
(3)

本文采用Hinton[18]提出的逐層預訓練—微調策略來解決深度網絡存在的非凸性和梯度彌散問題。每個SAE的非線性變換關系,特征與目標標簽之間的關系將通過逐層貪婪訓練得到有效學習。將所有SAE按照圖5從左到右的順序分別獨立訓練,且上一個SAE提取到的特征將作為下一個SAE的輸入。當第l層的SAE訓練完畢后,第l層的隱藏層特征將作為Softmax分類器的輸入,對Softmax分類器進行訓練,獲得最佳參數矩陣。最后,所有SAE將會被組合成一個SSAE進行整體微調。
微調過程旨在了解各層之間的相互關系,使目標標簽和預測標簽之間的誤差最小化。在迭代過程中,根據FP和BP算法計算代價函數對前L-1層網絡參數的導數,由式(4)對J(θ)求導得到代價函數對最后的Softmax層參數的導數。在微調之后,對SSAE從輸入層到最后一個SAE特征層進行切割,提取用電特征F。
(4)

圖4 堆疊稀疏自編碼器結構
1.3 基于Hellinger distance的改進DF分類識別
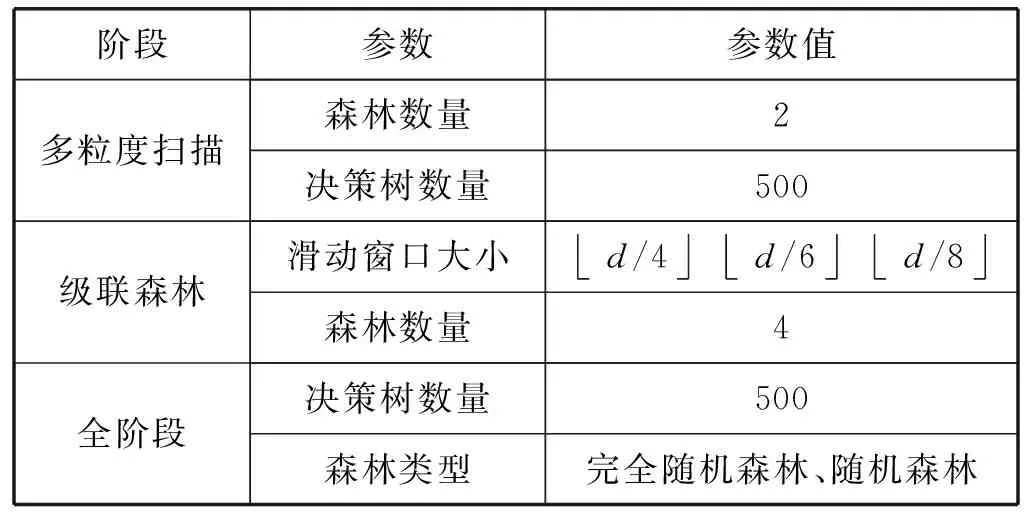
將從SSAE中提取的用電數據特征和相應的標簽一起用于DF的訓練。受深度神經網絡啟發,DF由多粒度掃描和級聯結構森林兩部分組成。如圖5所示。

(a) 多粒度掃描階段

(b) 級聯森林階段圖5 Deep Forest算法流程
多粒度掃描采用滑動窗口結構對數據集進行掃描擴展,生成原始數據的特征以增強級聯森林的差異性。在圖5中,假設經SSAE提取后得到的用電特征序列為n維,取窗口大小為d,步長為1(僅作示例)進行滑動掃描,得到k=(n-d)/c+1個d維實例向量。這k個d維向量被用于訓練兩個類型的森林,因為竊電檢測屬于二分類問題,因此訓練后將得到2維類別概率向量。隨后將2維類別概率向量按序拼接作為級聯森林的輸入向量。
采用經多粒度掃描所得的類別概率向量作為級聯森林的輸入向量。首先,輸入向量經不同類型的森林模型分類訓練后將得到增強特征向量。隨后,增強特征向量將與原始輸入向量拼接,輸入到級聯森林的下一層。特別地,級聯層在擴展到下一層后,將通過驗證集對整體級聯的性能進行估計,若沒有明顯的性能提升,則終止該訓練過程。因此,級聯結構中的層數具有自適應性,這使得該算法適用于不同規模的數據集。最后,對輸出的類別概率向量取均值和最值,得到最終的分類結果。
級聯結構通過對原始特征向量進行逐層處理實現表征學習的思想。它并不像DNN那樣根據正向和反向傳播算法來逐層學習,而是在有監督學習下通過基于決策樹集成的集成來直接學習類分布特征。DF結構中森林決策樹一般采用分類回歸決策樹(Classification and regression tree,CART),CART決策樹以最小Gini指數作為分裂屬性,Gini指數的計算如下:
(5)
式中:p(i|t)為變量t屬于類i的概率,c為樣本的個數。Gini指數越小劃分效果越好。然而,原始DF算法大部分工作都考慮在相對平衡的數據集上,忽略了不平衡樣本數量的情況。已有相關研究證明了Gini指數非均衡敏感的固有弱點[19],因此將Gini指數作為分裂標準會導致出現信息增益很小甚至負增長的情況,降低分裂屬性選擇的有效性,導致決策樹過快停止生長[20]。最終分類器往往會傾向于有利于多數正常用戶分類的方向學習,使少數類竊電用戶無法得到有效劃分。
為了克服上述缺點,本文考慮基于距離度量作為決策樹的分裂標準。Hellinger distance度量了兩個分布之間的距離,是一種反映不同概率分布差異的度量方法,用于計算給定屬性在不同條件下的類概率分布之間的差異,然后選擇差異大的屬性作為最佳分裂指標,改進了Gini指數在不平衡分類情況下的不足[20]。
設(Θ,λ)為度量空間,P、Q分別表示對應參數λ的兩個連續分布。則P、Q兩分布之間的Hellinger distance表示為:
(6)
當分布是離散型時,在可數空間Φ中,Hellinger distance又可表示為:
(7)
Hellinger distance具有如下的性質:

(2) 為對稱非負(即:dH(P,Q)=dH(Q,P)≥0)。
(3) 值越大,表示概率分布P和Q之間的差異也越大。
(4) Hellinger distance的平方是KL散度的下界。
采用式(7)作為分裂指標時,由于是在可數空間上求值,上述條件概率下的分布可表示為:
(8)
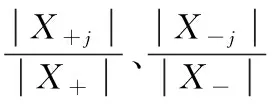
2 結合SSAE與HDDF的竊電用戶檢測模型
本文以用戶用電特征樣本為輸入,樣本分類結果為輸出的方式實現對用戶用電行為的檢測。具體可分為以下7個步驟:
(1) 按8 ∶2比例隨機劃分用電量數據集為訓練樣本和測試樣本。
(2) 對原始數據集進行預處理。
(3) 將訓練樣本中的用戶用電量數據輸入SSAE網絡。對SSAE采用逐層貪婪訓練—微調的方式進行訓練(算法1)。
(4) 對SSAE從輸入層到最后一個SAE特征層進行切割,提取用電特征F。
(5) 將經SSAE提取到的用電特征F及對應標簽輸入DF進行訓練,采用Hellinger Distance優化DF,輸出指示是否竊電的標簽(算法2和算法3)。
(6) 訓練完畢,得到用戶竊電行為分類檢測的模型。
(7) 在測試集上評估本文所提模型與其他對比模型的性能。
算法1SSAE用電特征提取
輸入:用戶電量數據X={X1,X2,…,XN}。
(1) 首先訓練網絡中的第1層,使用FP及BP算法,通過如下公式得到本層的參數W、b:
(9)
(10)
(11)
(12)
式中:δ(l)為第l層的殘差、a(l)為第l層的激活值。
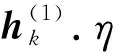
(13)
(14)
(15)
(4) 將第n個隱藏層的特征值輸入Softmax分類器進行訓練,通過計算式(16),最小化目標標簽與預測類標簽之間的誤差來獲得最佳參數矩陣。
(16)
(5) 將所有訓練好的SAE提取出來進行堆疊組合,進行微調。
(6) 將由逐層貪婪預訓練得到的參數作為SSAE網絡的初始化權重值。
(7) 計算每層的激活向量a(l)與殘差δ(l)。
(8) 將殘差從Softmax分類器層傳回輸入層。使用梯度下降算法微調每一次迭代后的參數W、b。
(9) 重復步驟2至步驟4,優化模型參數,直至代價函數滿足收斂要求。
算法2HD決策樹改進Deep Forest
輸入:訓練集T,終止值C,屬性集合F。
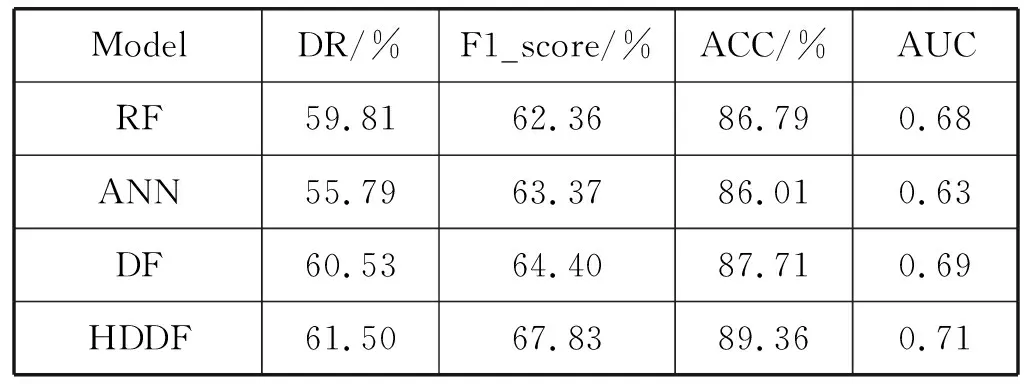
(1) if |T| (2) return; (3) end if (4) for屬性集F的每個特征屬性fdo (5) 由式(8)計算屬性f的Hf=Hellinger(T,f); (6) end for (7)b=max(H); (8) for屬性b中每個值vdo (9)HDDT(Txb=v,C,F); (10) end for 算法3改進的DF竊電用戶識別 輸入:經SSAE提取到的用電特征F及對應標簽。 輸出:指示是否竊電的標簽。 (1) 設置1個d維的窗口在輸入的用電特征向量上進行滑動取值,步長為c,則切分成k個d維向量(k=(n-d)/c+1)。 (2) 將k個d維向量輸入兩種類型的森林進行訓練,每個森林各輸出k個2維類別概率向量。 (5) 將這8維增強向量與原始輸入用電特征進行拼接,組成4×k+8維的特征向量,作為下一層級聯森林2的輸入。 (6) 判斷模型性能,若性能無明顯提升,則進入下一步;若性能仍有上升,則繼續進行訓練。 (7) 輸出末級訓練得到的類別概率向量。先求其均值再取概率類別值最大的類作為是否竊電的分類結果。 圖6 基于SSAE-HDDF的竊電檢測模型框架 在本文所提的SSAE-HDDF模型中,由于對SSAE網絡進行逐層貪婪訓練得到整個網絡的初始化參數,再利用微調手段優化整體網絡性能,因此能充分提取到用電數據關鍵特征。隨后再將提取出的用電特征作為分類器的輸入進行分類識別。使用Hellinger distance優化DF分類器,從式(8)可以看出不受先驗概率的影響,對不平衡數據類分布不是很敏感。將SSAE特征提取器與HDDF分類器相結合,由于對原始用電數據進行了特征再表征,加強了特征與標簽屬性間的非線性映射關系,進一步提高HDDF的分類表征學習能力[2]。 本文選取的數據集來自于國家電網公司某地9 956個用戶2015/01/01—2015/12/31的日用電量數據。圖7顯示了數據集的一部分。其中,CONS_NO為用戶編號,label表示用戶類型(0為正常,1為竊電),DATA_DATE則表示日期,KWH_READING代表當天用電量,KWH_READING代表前一天用電量,KWH為當天用電量與前一天用電量示值差。特別地,本數據集是典型的不平衡數據集,正常用戶與竊電用戶樣本比例為8 561 ∶1 395。 圖7 部分用戶用電量數據 由于設備故障、數據傳輸故障,人為主觀因素等多方面原因,造成部分用戶數據存在異常值和缺失值(其中10月份數據大量缺失)。對于異常值,采取視為缺失值處理的方法。對數據缺失百分比高于60%的用戶進行剔除。對低于60%的用戶,則通過簡單移動平均窗口法進行插補。簡單移動平均窗口方法根據時間序列逐項計算固定數量項的一組平均值,并作為下一個缺失值的填充。即一組數中的第i個位置數據為缺失數據,則取前后window個數據的平均值作為插補數據。這里window取為5。按下式計算缺失值: (17) 若出現有連續的超過5個NaN值輸入的特殊情況,則在這些輸入中插入該行的平均值,然后再執行上述補值操作。按下式對數據進行歸一化處理: (18) 經過預處理后的數據集中包含7 869個正常用戶樣本,1 154個竊電用戶樣本。 在竊電檢測中,錯分正常用戶與竊電用戶,后果是不同的。將正常用戶誤報為竊電用戶可能使正常用戶遭受不必要的經濟損失,影響用戶的信用,也會增加核查成本;而將竊電用戶錯分為正常用戶不僅使竊電用戶逃脫應受的懲罰,也讓電力企業承擔嚴重的經濟損失。在保證總的評估性能的基礎上,應當注重對竊電用戶樣本的評估。為了平衡上述兩種錯誤本文采用了4個指標進行性能評估,分別為檢出率(Detection rate,DR)、準確率(ACC)、F1-Score和AUC。其中F1-Score是一種混合度量,常在不平衡樣本分類中調和精確率和召回率。在AUC中,M為正類樣本的數目,N為負類樣本的數目。相應的混淆矩陣如表1所示。 表1 混淆矩陣在竊電檢測中的應用 (19) (20) (21) (22) (23) 本文所提模型參數主要為特征提取階段中SSAE隱藏層維數以及DF相關參數。在SSAE網絡結構中,輸入層節點數為每個用戶304天(不包含10月)的用電量數據。文獻[22]中指出,一般將隱藏層設為三層可取得良好效果,故本文使用含有三層隱藏層的SSAE。SAE的學習率η=0.01,稀疏性參數ρ=0.05,微調學習率取值為0.2。 采用文獻[1]的方法,在進行特征提取的過程中應盡量最小化每個SAE的損失函數并減少每個SAE的輸出特征維度。圖8顯示了每個SAE的LSAE與其特征層維數的關系。對于圖8(a)SAE而言,拐點為(125,0.985 8),當其特征層維數大于125以后,LSAE幾乎保持不變,故選擇125作為該特征層的維數。類似地,圖9(b)、(c)的特征層維數分別為45、20。 (a) 特征維數 (b) 特征維數 (c) 特征維數圖8 特征維數與LSAE的關系 DF具有無須大量設置參數和調參的優點,采用默認的參數設置即可。因此,本文采用DF默認的參數設置并結合實際情況稍作調整。具體參數設置見表2。 表2 DF參數 3.3.1特征提取的對比與分析 為了評估SSAE特征提取能力,采用了其他四個常用的特征提取方法與HDDF分類器結合作為對照組。即基于統計的特征提取方法、普通AE、PCA、獨立成分分析(Independent component analysis,ICA),以及未經微調的SSAE。 按照基于統計的特征提取方法[6-7],提取年、季度、月,不同階段的用戶用電特征,見表3。不同特征維度下準確率的變化如圖9所示。 表3 統計特征指標 圖9 統計特征維度對準確率影響 圖9中,隨著特征維度的增加,準確率逐步上升,當特征維度為30時達到最高,此后準確率有所下降。這是因為各特征的屬性有所關聯,所提供的有效信息重疊,特征的增加有可能帶來冗余信息干擾以致準確率下降。 為了使對比更加合理,設定AE、PCA和ICA所提取到的特征均為20維,而基于統計提取的特征,使用PCA降維至20維。不同特征提取方法的對比結果如表4所示。 表4 不同特征提取方法對比 由表4可知,SSAE(微調)在每一項評價指標上均優于其他方法。以DR為例,SSAE(微調)比SSAE、PCA、ICA、AE、統計方法分別提高了6.75%、17.45%、19.31%、16.96%和25.82%。不同特征提取方法的結果表明,基于統計方法提取的特征只是從統計量的角度提取了表層如標準差、均值等特征,未能提取到隱含的深層特征,因而效果不及其他方法。普通自編碼器網絡的特征尋找能力強于PCA與ICA,這是因為神經網絡能夠學習非線性關系也能表征非線性變換,因而能比PCA、ICA提高對許多復雜非線性映射問題的泛化學習能力。深度結構的神經網絡性能又優于普通神經網絡,SSAE因為其稀疏特點和深層網絡結構對特征輸入進行高效的表征學習,提升了分類精度,因而表現最好。此外,微調策略加強了整體網絡充分提取有用特征信息的能力。 3.3.2模型性能的對比與分析 為驗證所提模型性能,本文建立了8種模型對比分析。包括RF、ANN、DF、HDDF、SSAE-RF、SSAE-ANN、SSAE-DF和SSAE-HDDF。其中,前4種模型未進行特征提取,后4種模型采用了SSAE模塊進行特征提取。結果如表5、表6所示。 表5 未經SSAE特征提取的模型分類結果 表6 經SSAE特征提取后的模型分類結果 實驗結果表明,本文所提SSAE-HDDF模型在四個評價指標上表現最佳,不僅具有較高的總體評估精度,同時能夠提高對竊電樣本的檢出。在圖10、圖11中,當樣本量較小時,SSAE-HDDF的DR值遠高于其他模型,隨著樣本比例的增加,SSAE-HDDF保持較為穩定的趨勢,說明該模型不太受樣本規模的影響。經SSAE提取后的模型性能總體優于未經SSAE提取過的模型,其中SSAE-HDDF最高可達73.49%,而最低的ANN僅有55.79%。原因在于SSAE的稀疏性和深層網絡結構能進行高效的表征學習,提供比原始數據更加有用的信息,進一步加強后續DF的分類學習能力。DF在Hellinger distance的引入下保證模型精度并且不受先驗概率的影響,對不平衡數據類分布不是很敏感,提高了模型在學習過程中對竊電樣本的重視程度,從而檢測出更多的竊電用戶。 圖10 未提取特征的模型DR值 圖11 經提取特征后的模型DR值 由于現有的竊電檢測方法多從電氣量角度提取統計特征,未能挖掘出深層隱含特征,且算法未考慮數據集的不平衡性,本文提出一種結合SSAE與HDDF的竊電檢測模型。在此模型中,SSAE類似于自動特征提取器,HDDF則是輸出分類器。對比實驗表明,提出的SSAE-HDDF模型具有兩個特性:首先是可以通過混合模型自動提取特征。與常見的特征提取方法相比,顯示了SSAE強大的自動特征提取能力。其次,采用Hellinger distance改進分類算法以克服樣本類別不平衡對分類結果的影響。HDDF在深度結構下可實現對輸入特征的多層表征學習,加強對竊電樣本的重視,提高了竊電樣本識別率。未來工作將會在特征工程上進行改進和完善,選取更為有貢獻的特征進一步提高竊電用戶的檢出率。


3 實驗與結果分析
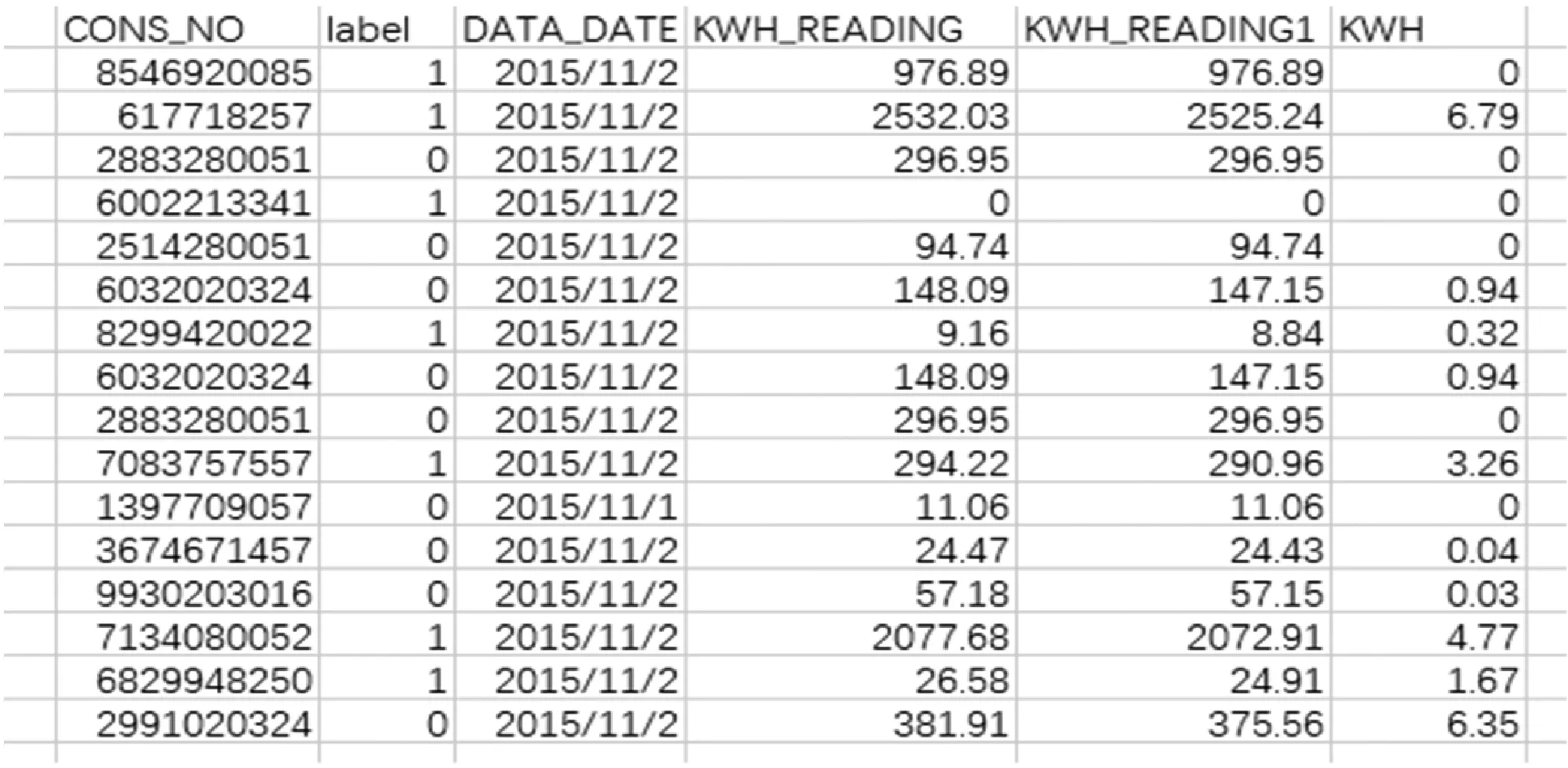
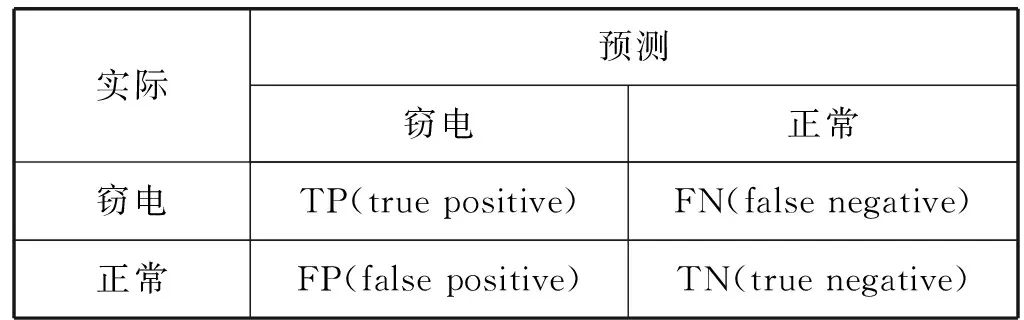
3.1 模型評價指標
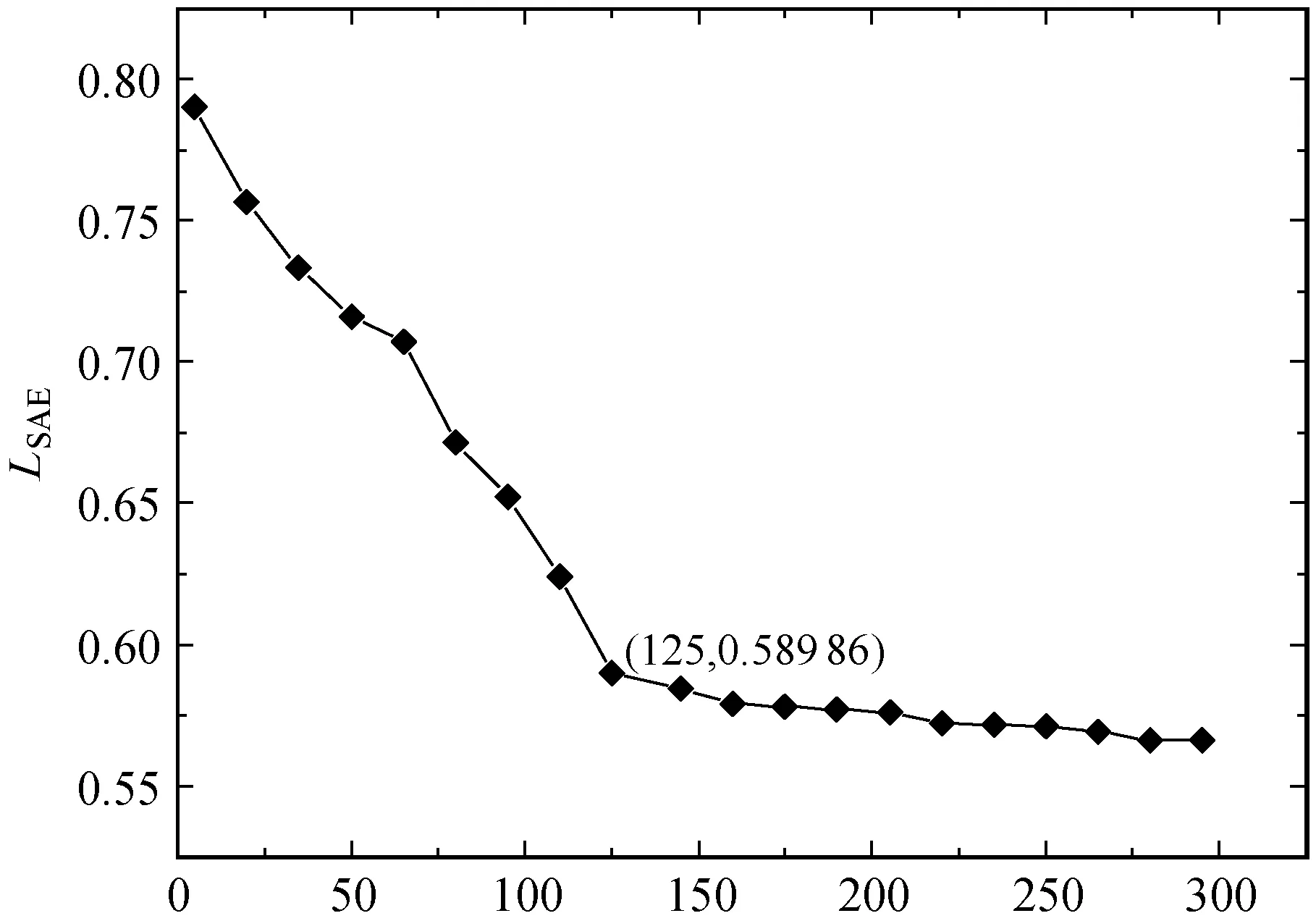
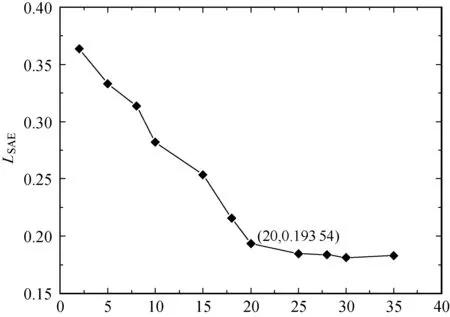
3.2 模型參數分析

3.3 對比結果與分析






4 結 語

