基于聯合算法的連續(xù)體結構拓撲優(yōu)化新方法
齊 峻,武 星
(長安大學工程機械學院,陜西 西安 710064)
0 引言
拓撲優(yōu)化算法自20世紀被提出以來,一直在不斷更新。拓撲優(yōu)化的目標是在滿足各種設計約束的情況下,找到材料的最優(yōu)分布[1]。雙向漸進結構優(yōu)化法(BESO)是一種將漸進結構優(yōu)化法(ESO)和材料添加策略算法(AESO)相結合的方法[2]。最初的ESO主要是去除最低應力單元,經過發(fā)展,BESO在ESO原有的基礎上可實現增加單元。原始的硬殺傷ESO/BESO方法消除了設計領域的元素,通常,作為設計變量的元件不能直接從設計領域中消除,除非軟元件完全等同于空心元件。換言之,對于一個新的拓撲優(yōu)化問題,開發(fā)一種軟殺傷BESO方法,然后探索硬殺傷元件的可能性可能會更可靠[3-5]。
近年來,遺傳算法(GAs)[6]也不斷地發(fā)展,并逐漸應用于拓撲優(yōu)化問題[7]。由于GAs的隨機性,其直接應用于拓撲優(yōu)化問題時會產生棋盤格現象。Liu等[8]很好地意識到了GAs和ESO結合的問題,但由于在設計過程中無法實現材料的增加,得到的結構可能無法滿足使用要求。Zuo等[9]提出了GAs和BESO相結合的拓撲優(yōu)化方法,實現了迭代過程中材料的增減。NSGA-II是在GAs的基礎上發(fā)展起來的,通過快速的非支配排序和擁擠計算、競爭選擇和精英策略來實現快速優(yōu)化過程。在全局優(yōu)化方面,NSGA-II顯現出比GAs更大的優(yōu)勢。
本文主要部分說明如下:第1節(jié),闡述了拓撲優(yōu)化的基本問題;第2節(jié),根據傳統的靈敏度分析,推導出了固體和軟單元的靈敏度數值;第3節(jié),簡要說明了本文程序的原理和數值實現;第4節(jié),通過具體的數值算例證明所提出的新方法的穩(wěn)定性和有效性。
1 問題陳述
在拓撲優(yōu)化問題中,往往追求給定體積分數下的最大剛度。剛度通常用應變能數值表示,對于具有n個離散單元的拓撲優(yōu)化問題可以表示為:

式中,C為平均柔度,在設計中,通過計算平均柔度來達到最大剛度。u為全局位移向量,K為全局剛度矩陣。vi是單元i的體積,V*是目標體積。
2 靈敏度數值計算和過濾方案
2.1 靈敏度數值計算
設計變量通過基于梯度的方法更新。對于單相固體材料-空洞優(yōu)化問題,通過推導目標函數可以得到單元靈敏度值:
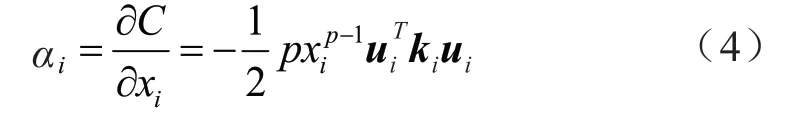
式中,p表示懲罰指數,xi表示單相固體材料的單元密度值,當某單元固相材料處于激發(fā)狀態(tài)時,xi=1,否則,關閉此激活狀態(tài),單元最終轉化為空洞狀態(tài),此時xi=xmin。ui表示第i個單元的位移矢量,ki表示第i個單元的剛度矩陣。
靈敏度值可用式(5)表示:
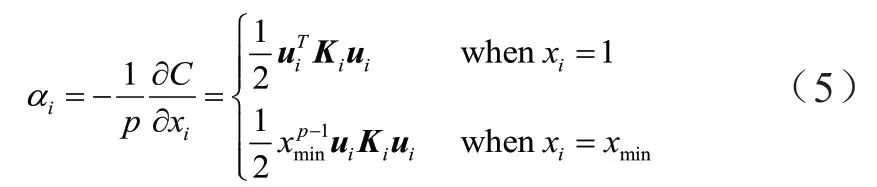
2.2 過濾方案
采用靈敏度濾波策略對靈敏度進行修正。這不僅有效減少了棋盤格現象,還通過過濾半徑內物理單元的靈敏度值推導出空單元的靈敏度,實現單元的增刪。本文的過濾策略是將與節(jié)點關聯的所有元素的靈敏度值均質化為節(jié)點的元素靈敏度值,如式(6)所示:

式中,H為設計域的節(jié)點總數,w(rik)為權重因子,rik表示元素i的中心到節(jié)點k的距離。權重因子可以表示為:

式中,rmin表示過濾器半徑。為了提高方法優(yōu)化的收斂性,采用考慮歷史迭代信息的收斂策略來修改靈敏度值。具體操作是計算本次迭代和上次迭代的靈敏度的平均值,將其作為靈敏度的更新值。
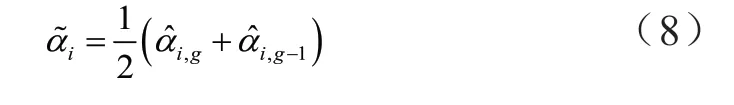
式中, ,?igα 和 ,1?ig-α 分別為單元i第g次和g-1次迭代的靈敏度值。最后,根據該靈敏度值測量各單元對結構性能的影響,然后將體積作為拓撲優(yōu)化設計的約束條件。
3 算法的提出與實現
3.1 算法提出
在本文提出的算法中,每個元素都被視為一個獨立的個體進行分析,在迭代過程中保持種群維數穩(wěn)定,允許新種群代替原種群,但不允許合并。每個單元都由一定長度的二進制字符串表示。初始字符串在本文中定義為全“1”的數組,表示所有單元均為固相材料。一個全為“0”的數組意味著該單元將在迭代中被刪除。數字“1”代表材料屬性的強度。交叉和變異算子只有“0”和“1”之間的轉換。
通過初始化種群,實現設計域內所有個體的編碼,單位編碼的初始值為長度為6的矩陣。對模型進行預處理后,按式(5)計算各元素的靈敏度值。此時,可以根據每個迭代步驟的目標體積分數設置靈敏度閾值,并根據元素靈敏度值進行排序。對于具有相同靈敏度的單元,計算它們的擁擠程度,使同級個體之間存在清晰的層級關系。如果種群中目標函數的最大值等于目標函數的最小值,則將種群的擁擠程度設置為無窮大。一般來說,擁擠的表達式如下:

3.2 算法實現
本文算法步驟如下:
1)通過有限元思想進行預處理,主要是網格劃分、施加載荷和設置邊界條件[10]。
2)初始化種群,個體由一系列“1”碼組成,根據靈敏度計算公式加上懲罰因子和過濾方案的實現來計算靈敏度。指定懲罰指數(p)和體積進化率(ER)等參數。
3)根據靈敏度值迭代進化種群。主要進行快速的非支配排序和交叉變異操作。
4)刪除設計域中單元基因串中僅包含數字“0”的元素。如果上次迭代中刪除的元素在當前生成中具有高靈敏度值,則將該元素添加到設計域中。
5)根據靈敏度級別和主導關系將實體材料屬性分配給設計域中的其余元素。
6)檢查設計域的剩余體積和收斂標準。
7)重復步驟2至步驟6,直到達到目標體積和收斂標準。
對于收斂準則,當滿足體積約束時,考慮了兩個連續(xù)優(yōu)化迭代之間最大柔順度的絕對變化,兩次連續(xù)優(yōu)化迭代的收斂性之差小于0.005。本文中S=5,即連續(xù)優(yōu)化迭代次數為5。

4 數值算例
本節(jié)通過數值算例來驗證本文提出的算法的有效性、穩(wěn)定性和優(yōu)越性。考慮了一種虛擬材料,材料的物理性質如表1所示。所涉及的算法均在Win10 Intel?CoreTM i5-9300 CPU、2.40 GHz、16 G運行內存的桌面上執(zhí)行。

表1 虛擬材料的物理性質
如圖1所示,考慮了尺寸為50 mm×30 mm的二維懸臂梁結構。懸臂梁結構左側完全固定,右側中間施加1 N的集中荷載。將體積約束設置為初始體積的35%。網格大小設置為1,共1 500個單元,懲罰指數p=3,過濾器半徑rmin=1.5 mm,體積進化率ER=0.02。

圖1 懸臂梁模型
4組懸臂梁結構最終迭代結果如圖2所示。從圖2可以看出,模型會產生良好的布局效果,邊界更清晰。由于NSGA-II具有隨機性,每次迭代的結果可能會有所不同,但比較4次運行的結果,結構布局顯示出相似之處。懸臂梁模型在設置相同參數條件下通過BESO方法所迭代優(yōu)化出的最終結果如圖3所示。4組懸臂梁最終平均柔度結果如表2所示。通過比較表2中4個運行結果的目標函數,相對于平均值的誤差和最大誤差均不超過1%,4個運行結果的最終體積分數為35%,滿足約束條件。通過數值算例分析,證明該算法具有良好的穩(wěn)定性和收斂性。

圖2 4組懸臂梁結構最終迭代結果

圖3 BESO方法下懸臂梁最終結果
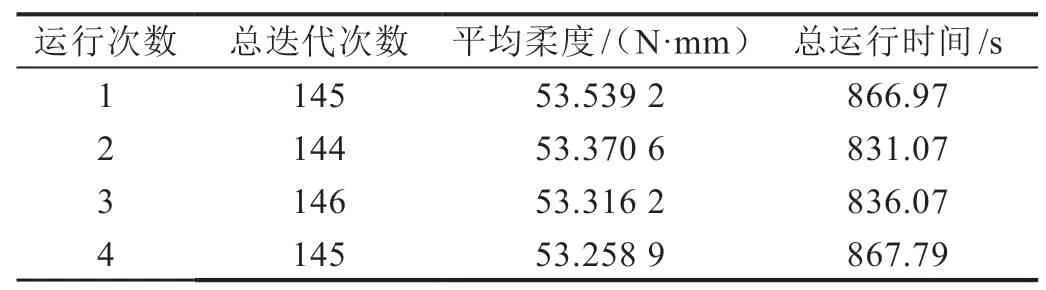
表2 4組懸臂梁最終平均柔度結果
與BESO方法相比,本文提出的新方法具有更強的進化能力。傳統的BESO方法在每次迭代過程中直接增刪滿足條件的單元,但不同的是本文提出的新方法引入了NSGA-II的演化機制。在迭代過程中,不會直接刪除敏感度閾值以下的單元格或增加單元格。相反,將“0”和“1”的數量用作添加和刪除的標準。不斷地通過“0”和“1”之間的演化,當一個單元出現全“0”的字符串時,就意味著一次刪除操作。該算法避免了每次迭代過程中的多次增刪改查,有利于算法逐步優(yōu)化直至收斂。
本文提出的新算法與原始BESO方法的對比如表3所示,設置相同的約束、材料和參數。由于本文提出的新方法具有很強的全局搜索能力,保證了優(yōu)化的效果。本文算法與原始BESO方法相比,整體在效果上和原始BESO方法近乎相同。考慮到遺傳算法具有隨機性,其在靈敏度計算、快速非支配排序這兩個方面每次的運行時間會較長,但是通過對比本文算法與原始BESO方法的總運行時間與總迭代次數,發(fā)現二者幾乎無差距,證明了本算法的效率和可靠性。

表3 懸臂梁最終平均柔度比較結果
5 結論
研究小組提出了一種新的結構輕量化設計拓撲優(yōu)化方法。通過將NSGA-II算法融入BESO方法中,保證了算法的全局優(yōu)化效果,實現了結構的剛度最大化,獲得了干凈的拓撲結構。通過數值算例分析,表明本文提出的新方法也能得到類似于BESO的結構布局,證明了算法的穩(wěn)定性和有效性。本文算法通過結合遺傳算法達到了全局最優(yōu)搜索的效果,在相同約束條件下與傳統BESO算法比較,發(fā)現本文算法可以提高結構剛度,證明了本文算法的優(yōu)越性。顯然,研究小組提出的方法可以更好地滿足復雜工況下的輕量化結構設計,可以應用于各個領域的工程問題,提高結構的性能,對工程結構的優(yōu)化具有指導意義。

