一種基于改進NSGA-II的多目標綠色柔性作業車間調度方法＊

鄭錦燦 邵立珍 雷雪梅

（①北京科技大學自動化學院，北京 100083；②北京科技大學順德創新院，廣東 佛山 528399；③北京科技大學信息化建設與管理辦公室，北京 100083）

柔性作業車間調度問題（flexible flow job shop scheduling problem，FJSP）是傳統作業車間調度問題基礎上的擴展，它是一類經典的NP-hard問題。在傳統作業車間調度問題中，每個工件由一道或多道具有固定加工順序的工序構成，且每道工序的加工機器是唯一的。FJSP允許一道工序有多臺可供選擇的加工機器，且在不同機器上的加工時間可能存在差異，這更符合柔性制造系統的實際情況。傳統的FJSP通常僅考慮單一的目標函數，如最小化最大完工時間或者經濟性能指標等。但是隨著社會經濟的快速發展和人們的環保意識不斷的提高，單純的經濟指標已經無法滿足綠色生產的需求，能耗、碳排放等一系列綠色生產指標正越來越受到企業的重視[1]。因此，多目標柔性綠色作業車間調度問題應運而生。

不同于單目標FJSP，多目標FJSP中多個性能指標需要被同時優化。許多學者采用智能優化算法求解該問題。Li M等[2]提出了一種兩層帝國競爭算法求解具有目標重要性約束的多目標優化問題。Msc M 等[3]應用分布式估計算法求解了多目標隨機調度問題。楊帆[4]提出了一種多種交叉混合的交叉方法和一種基于元胞數組的解碼方式，提高遺傳算法的全局搜索能力。梁曉磊等[5]構建了以機器效率最大和最大完工時間最小為目標的調度模型，并使用改進的遺傳算法求解。Chang H C等[6]提出了一種混合遺傳算法（hybrid genetic algorithm，HGA），使用田口方法來優化算法的參數，還提出了一種新的編碼機制解決了無效工件的分配問題。

在多目標調度問題的求解中，如何防止算法陷入局部最優是研究的一個熱點。文笑雨等[7]設計了N5鄰域結構，并提出了改進NSGA-II求解方法。張國輝等[8]考慮了完工時間，機器負載以及環境碳排放的柔性低碳調度模型，在NSGA-II算法基礎上引入鄰域搜索策略得到了高效可行的調度解。Frutos M等[9]構建了最小化完工時間和總成本的多目標模型，在遺傳算法的搜索過程中引入模擬退火算法跳出了局部最優。陳輔斌等[10]結合實際生產過程中加工時間、機器負載、運行成本等情況，建立了多目標調度模型，引入免疫平衡原理改進NSGAII算法，避免了算法陷入局部最優。

雖然上述的研究取得了一定的成果，但是針對多目標FJSP的研究，仍存在如下問題：①現有的FJSP模型大都集中于最小化完工時間和機器總負荷，忽視了能耗指標，模型無法滿足實際的綠色生產需求；②在智能優化算法中，隨機選擇的初始化策略影響著算法的求解性能，但現有的智能優化調度算法對種群初始化策略關注較少，且解易于陷入局部最優。

基于上述考慮，本文首先建立了一個多目標綠色FJSP模型。模型中，除了考慮傳統的經濟指標，還考慮了能耗指標。其次，提出了一種改進的快速非支配排序遺傳算法（improved non-dominated sorting genetic algorithm II，INSGA-II）求解該模型。

1 多目標柔性作業車間調度問題

1.1 問題描述

FJSP的數學描述[11]為：有n個相互獨立的工件 J ={J1,J2, ··· ,Jn}在m臺不同的機器構成的機器集M={M1,M2, ···,Mm}上加工，每個工件包含一定的工序，以工序集 O ={Oi,1,Oi,2, ···,Oi,ni}的形式表示，預先給定所有工序在可選機器上的加工時間進行加工。

在建立具體的數學模型之前，根據實際的生產加工情況做出如下假設：

（1）同一時間內每個機器只能加工一道工序。

（2）所有工件的工序加工時間是已知的。

（3）同一工件的不同加工工序具有先后優先級，不同工件的加工工序沒有先后優先級。

（4）一道工序一旦開始加工就不能中止。

（5）每個工件在同一時刻內只允許在一道機器上加工。

（6）在0時刻開始所有機器都是可用的，同時機器不會發生故障。

本文中出現的一些符號定義如表1所示。

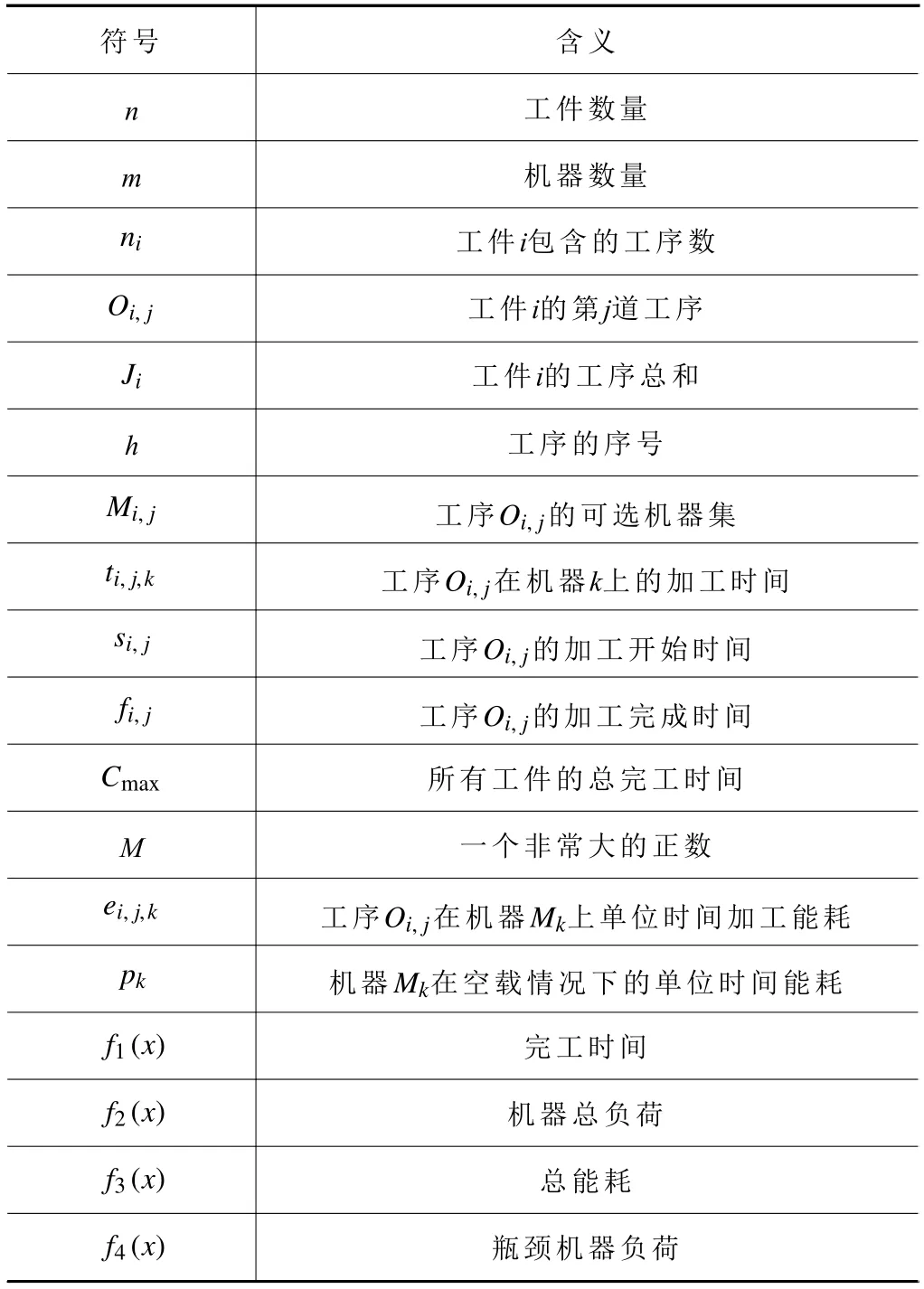
表1 符號定義表

1.2 模型建立

FJSP的數學模型如下：

式（1）和（2）均是控制約束變量，用來約束指定機器上的加工和工序。式（3）和（4）表示根據每一工件的工藝路線，工序的先后加工順序約束；式（5）表示每一個工件的完工時間不能超過總的完工時間；式（6）規定每臺機器某一時刻只能加工一道工序；式（7）是獨占性約束，即規定某一時刻每道工序僅能在一臺機器上加工；式（8）和（9）中規定各個參數的變量必須是正數。

模型中的優化目標為：最大完工時間、機器總負荷、能耗。最大完工時間是使用頻率最高的基本經濟指標；機器總負荷指標和瓶頸機器負荷指標在延長機器的壽命、合理分配資源以及提高生產效率的方面中有著重要的意義；能耗指標作為綠色生產的評價指標引入。計算公式如下：

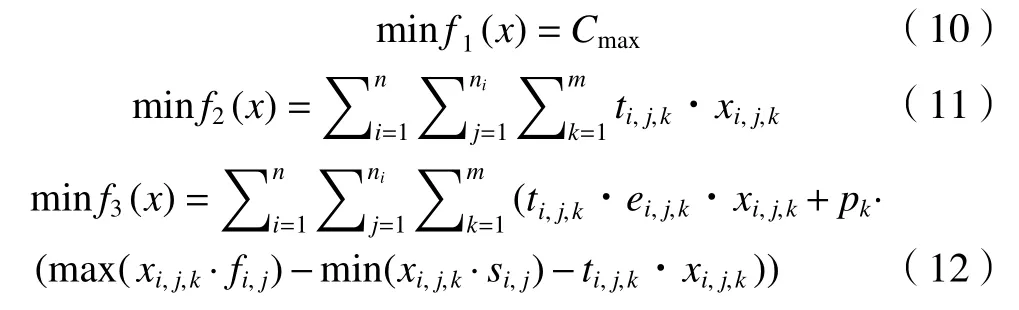
除了上述的3個性能指標，在進行算法的性能比較時，通常也會引入機器的瓶頸負荷指標進行測試，其具體計算公式如下。

2 改進的NSGA-II算法

INSGA-II算法的流程圖如圖1所示。該算法基于NSGA-II進行改進，主要包括以下幾個部分：編碼生成初始種群、解碼、快速非支配排序和擁擠度距離計算、交叉變異操作、精英保留策略和學習機制。

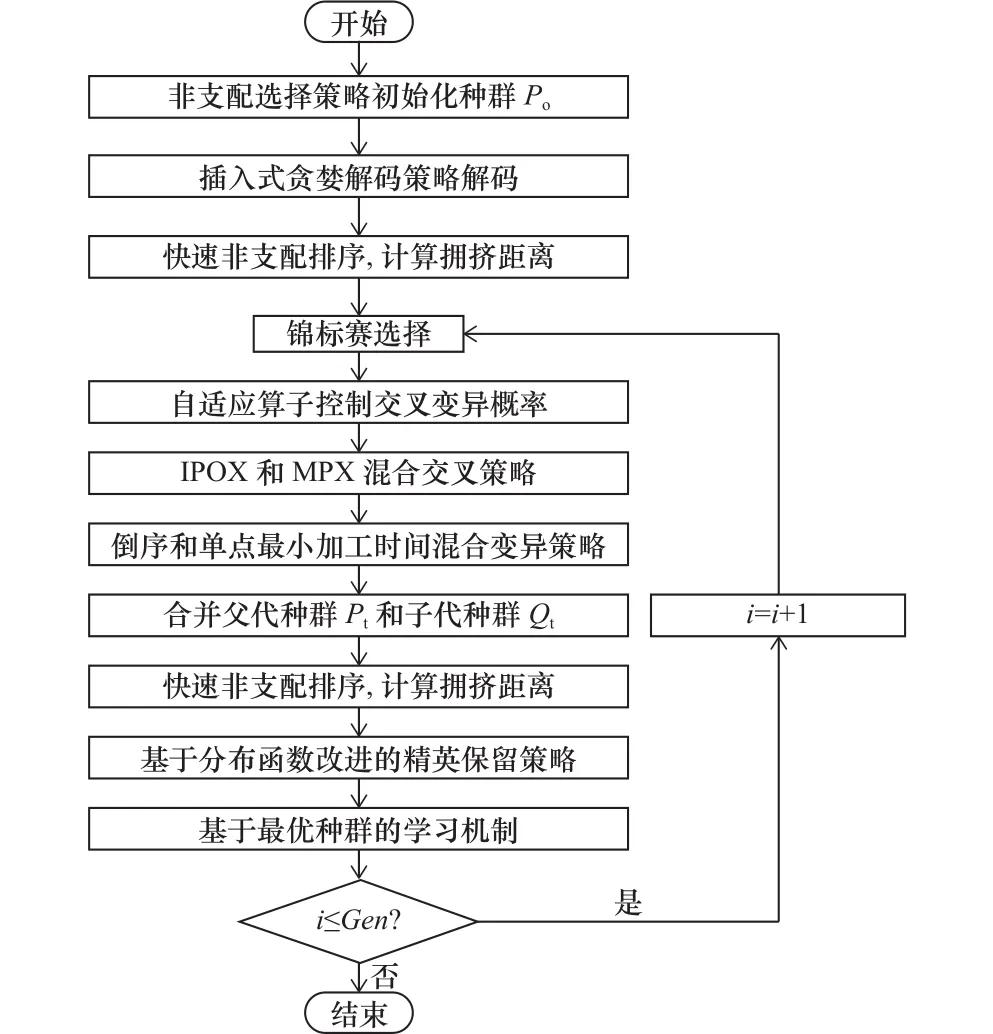
圖1 改進NSGA-II算法流程圖

2.1 混合種群初始化策略

種群的初始化方式與調度的初始解具有不可分割的關系，高效的初始化方式有助于提高算法的收斂速度，通過更少的迭代次數得到問題的最優解。

本文基于機器和工序（machine selection and operation sequence，MSOS)兩層編碼。如圖2，首先隨機生成工序染色體P，然后通過工序染色體P確定機器染色體M，圖中工序染色體[1, 2, 3, 1, 4, 2, 3, 4, 2]依次代表工序 [O11,O21,O31,O12,O41,O22,O32,O42,O23]，機器染色體[5, 1, 2, 4, 3, 3, 1, 2, 5]依次代表機器[M5,M1,M2,M4,M3,M3,M1,M2,M5]。

圖2 MSOS編碼示意圖

在MSOS編碼的基礎上采用一種基于全局、局部、隨機初始化的非支配選擇種群初始化策略。其中，全局選擇通過平衡全局的機器負載來實現全局負載最小化；局部選擇注重單一工件的工序最小加工時間，從而保證局部工序的加工時間最短；隨機選擇初始化隨機產生總工序長度的工序集，再通過對應工序可選機器集隨機選擇一個機器形成機器集，保證初始種群具有一定的隨機性。具體的初始化方法如下：

步驟1：分別執行局部初始化和全局初始化，產生兩個種群數量均為Np的初始父代種群。

步驟2：合并兩個初始父代種群，使用快速非支配排序的方法對父代種群進行初始排序篩選，刪除父代種群中完全相同的初始個體。

步驟3：在初始個體被刪除后，如果剩余的總種群數量少于Np則使用隨機方法初始化父代種群進行補充，直到種群的數量等于Np。如果剩余的種群數量等于大于Np，則選擇前Np個個體作為父代的初始種群。

2.2 解碼

解碼操作是指將編碼生成的初始種群染色體轉換成為可行的調度方案。本文中采用一種考慮機器空余時間的插入式貪婪解碼策略[12]，生成主動調度解，從而最大化的利用機器資源。

2.3 交叉與變異

本文采用改進優先工序交叉算子（improved precedence operation crossover, IPOX）和多點保留交叉算子（multipoint preservative crossover, MPX ），以及單點最小加工時間機器突變和倒序變異的混合交叉變異方式來提高算法的尋優能力，同時設置了自適應的交叉變異算子。

2.3.1 基于工序的IPOX交叉

步驟1：將所有的工件p隨機分配到兩個數據集R1和R2，使得

步驟2：子代C1中復制父代P1包含在R1中的工序基因，子代C2復制父代P2包含在R2中的工件，保持復制前后的工序基因的位置不發生變化。

步驟3：子代C1之中空余的基因位置用父代P2不包含在R1中的工序基因依次填入，子代C2之中空余的基因位置用父代P1不包含在R2中的工序基因依次填入。

IPOX交叉方式的示意圖如圖3所示。

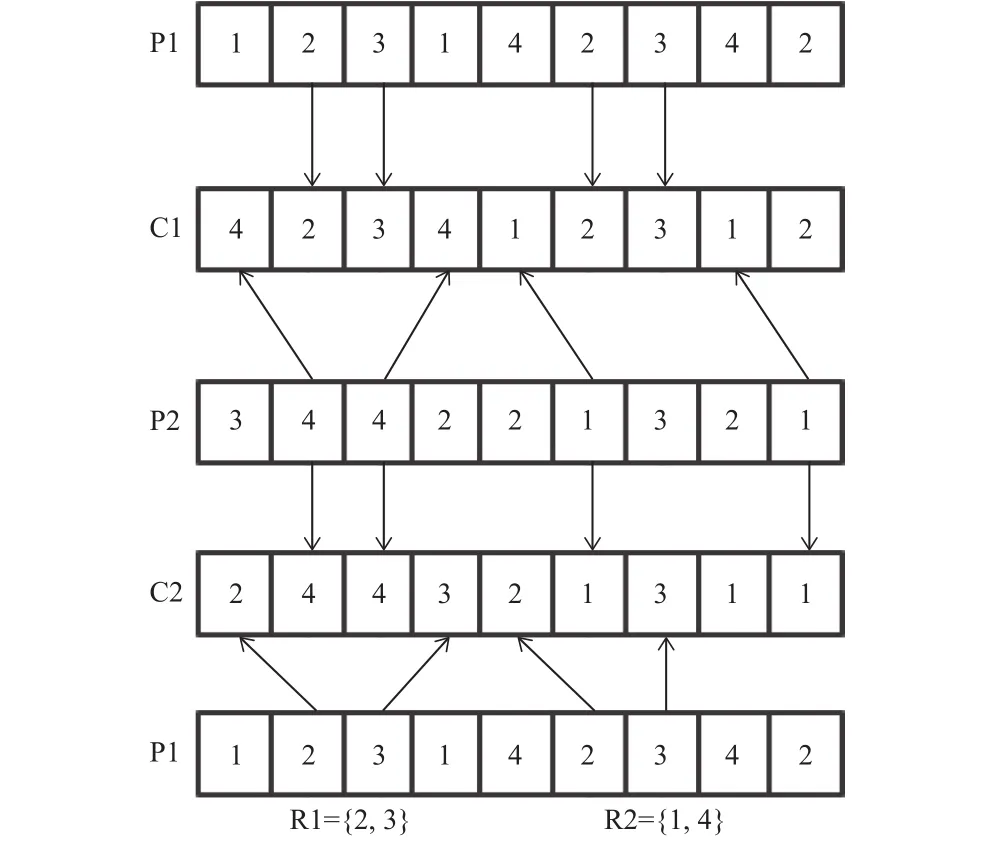
圖3 IPOX交叉示意圖

2.3.2 基于機器的MPX交叉

步驟1：隨機生成一個長度為總工序數只包含0和1的數組R3。

步驟2：隨機選擇兩條父代機器染色體M1和M2，交換M1和M2在R3數組出現數字1的相同位置，產生子代的機器集。

MPX交叉方式示意圖如圖4所示。

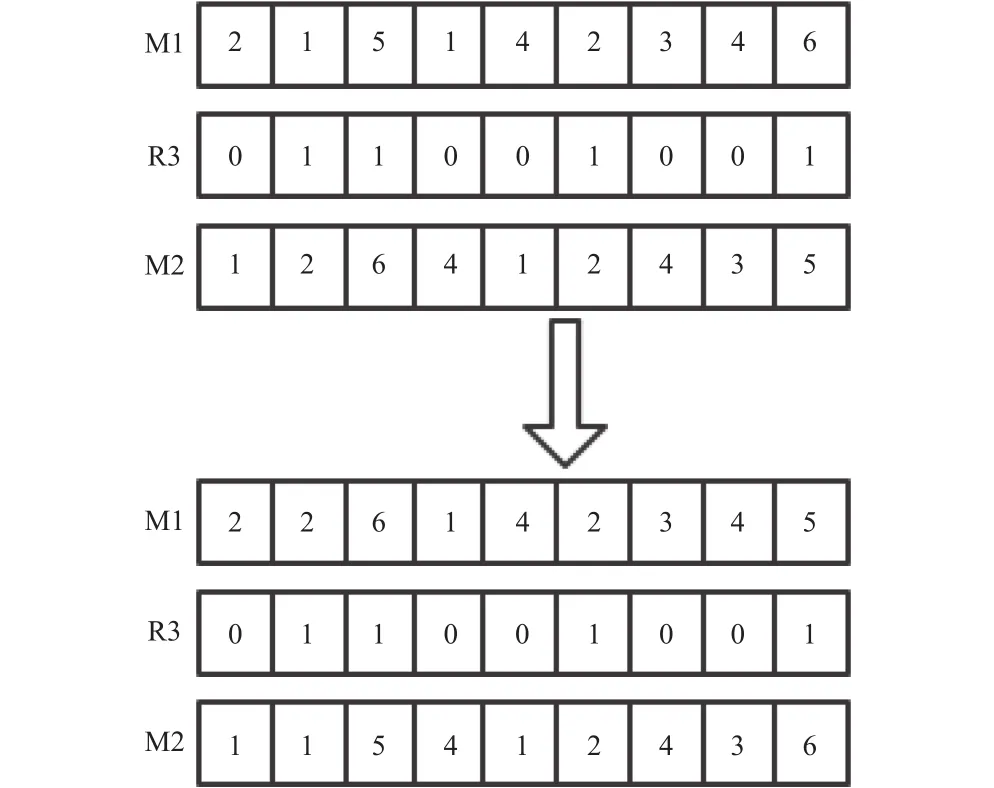
圖4 MPX交叉示意圖

2.3.3 混合變異策略

本文采用基于工序的倒序變異方式以及基于機器的單點最小加工時間突變的混合變異策略。基于工序的倒序變異，通過隨機在工序染色體選擇兩個變異位置，然后倒序交換這之間的染色體片段。基于機器的單點最小加工時間突變，通過隨機選擇一個工序染色體位置，找到其對應的機器染色體片段，將對應的機器染色體片段替換為該工序在可選機器集中具有最小加工時間的機器。

2.4 自適應交叉變異算子

本文中采用基于迭代的自適應交叉變異算子來控制交叉和變異的概率。Pc(i)和Pm(i)分別表示每代的交叉和變異的概率，其具體的計算公式如下。

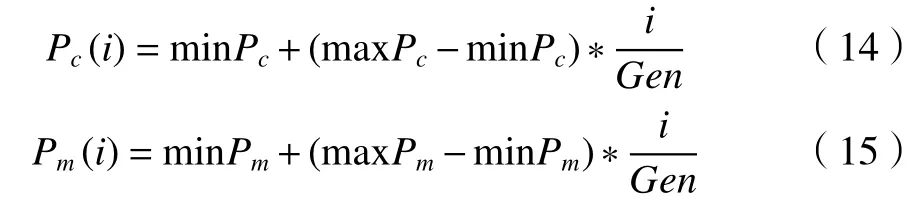
2.5 快速非支配排序與擁擠度算子

多目標優化問題的多個目標函數之間往往存在沖突，本文采用非支配排序和擁擠度算子對各個解集進行分層排序，從而區分出解集的優劣。

2.6 改進的精英保留策略

傳統NSGA-II采用隱性的精英保留策略，這樣容易導致后代出現大量的解處于第一非支配等級，同時解集之間的相似度也會較高。

本文提出一種動態調節的改進精英保留策略，控制算法迭代產生的后代種群，引入一個分布函數來限制父代種群中的精英數量，該分布函數通過兩種策略進行動態調節。

當算法的迭代規模較小時，子代非支配等級為1的精英數量較少。此時希望盡可能的保留父代迭代得到的精英解，讓子代繼承這些優良特性。而針對第2-N個非支配的等級的種群，則使用比例系數λ1進行選擇，如果某一支配等級選擇后種群數之和超過了N，則該非支配等級依據擁擠比較算子選擇個體數量，維持種群數量N保持不變。將這一閾值設定為子代非支配等級為1的精英數量小于父代種群規模的50%， λ1=0.5。此時精英保留策略如圖5，其中Pt和Qt分別表示當前代數的父代種群和子代種群，Pt+1和Qt+1分別表示下一代的父代種群和子代種群。Pt+1的計算公式如下:

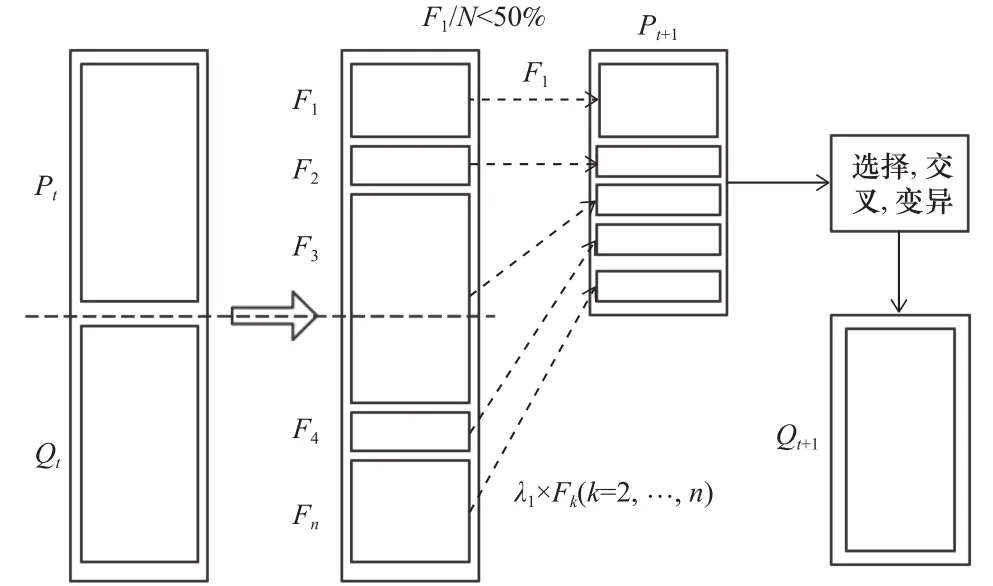
圖5 第一種條件下的改進精英保留策略

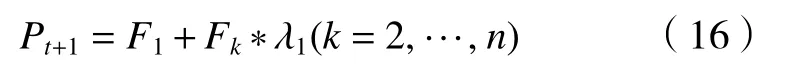
當算法迭代到一定的規模時，子代非支配等級為1的精英數量已經較多，算法的迭代可能陷入停滯。此時使用比例系數 λ2來選擇所有非支配等級的種群，以更多的比例接受一定程度的劣解，提高后代種群的多樣性，防止算法陷入局部最優，同時我們也需要控制種群數量。設置 λ2的參數為0.6，此時精英保留策略如圖6，Pt+1的計算公式如下。

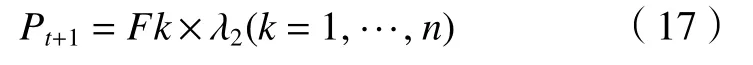
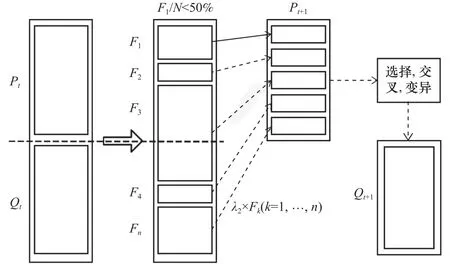
圖6 第二種條件下的改進精英保留策略

2.7 學習機制

NSGA-II的交叉變異算子在一定程度上可以防止算法陷入局部最優。為了提高算法的可靠性，采用一種基于最優個體的學習機制，針對算法迭代產生的優良種群進行鄰域搜索，具體的執行過程如下：

步驟1：選擇一條父代迭代后生成解集中支配等級為1的染色體P_1。

步驟2：在染色體上隨機生成兩個位置點A和B，記錄兩點之間的片段做為父代優良的基因片段。

步驟3：分別打亂A點左側的基因片段和B點右側的基因片段，重新組合生成新的染色體P_2。

步驟4：檢查P_2染色體的調度的可行性，如果產生了不可行調度的解，則為其不可行工序在可選機器集中分配一臺機器加工。確保染色體能夠生成可行調度解后計算P_2目標函數值和非支配等級。

步驟5：比較P_1和P_2的目標函數值和非支配等級，如果P_2優于P_1則使用P_2替換P_1來調整新的父代種群。

學習機制的示意圖如圖7所示。

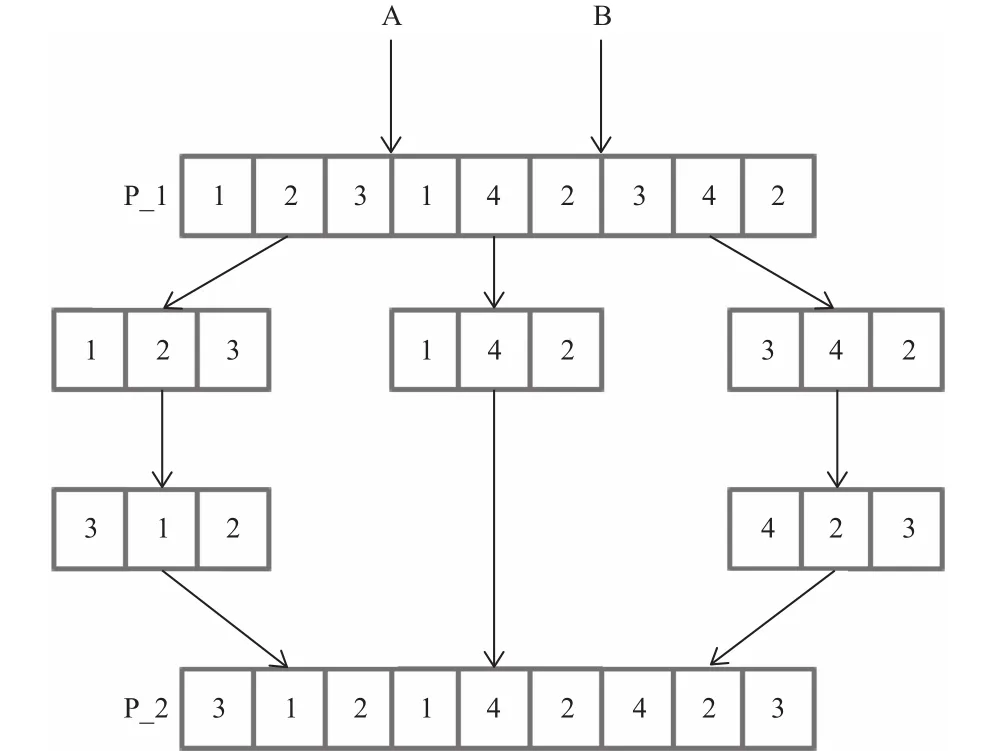
圖7 學習機制示意圖

3 算法仿真測試與分析

本文算法基于Matlab R2015a進行編程，并在Windows 10，AMD Ryzen 7-5800H，CPU 3.2 GHz，內存16 GB，64位操作系統上運行。設置算法的初始種群數量為100，最大迭代代數為200，交叉算子Pc的范圍為[0.4,0.8]，變異算子Pm的范圍為[0.01,0.1]。

3.1 改進初始化策略的有效性

為了驗證本文所提出的改進初始化策略的有效性，使用隨機初始化的NSGA-II算法和采用非支配選擇策略INSGA-II算法做對比，以Brandimarte基準算例中的MK04數據集為例，設定目標函數為最小化最大完工時間，最小化瓶頸機器負荷，最小化總負荷，其余的所有參數均保持一致，兩種算法各獨立運行20次，選取最優的結果繪制進化曲線進行對比。

由圖8～10可知使用非支配選擇初始化策略INSGA-II算法在初始解集上均優于使用隨機初始化策略的NSGA-II算法，同時其收斂的速度也較NSGA-II有一定的優勢。通過對比算法在各個目標函數上的最終解集收斂值，INSGA-II在機器總負荷以及最大完工時間上均優于NSGA-II算法，說明了非支配選擇初始化策略在求解該問題上較優。

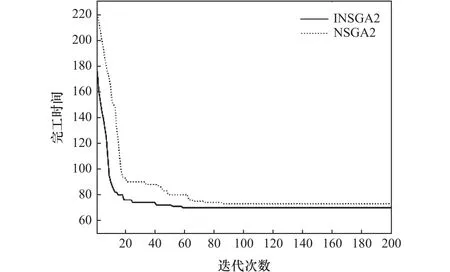
圖8 INSGA-II和NSGA-II完工時間進化過程

3.2 改進精英保留策略的有效性

為了驗證本文所提出的改進精英保留策略的有效性，選取使用傳統精英保留策略的NSGA-II算法與改進式精英保留策略的INSGA-II算法做對比，其余參數條件保持一致。選取Brandimarte中MK01的數據集進行測試，優化目標為最小化最大完工時間，最小化瓶頸機器負荷，最小化總負荷。兩種算法獨立運行20次，選擇最好的非支配解集個數進行記錄，如表2所示。

表2 MK01算例對比表

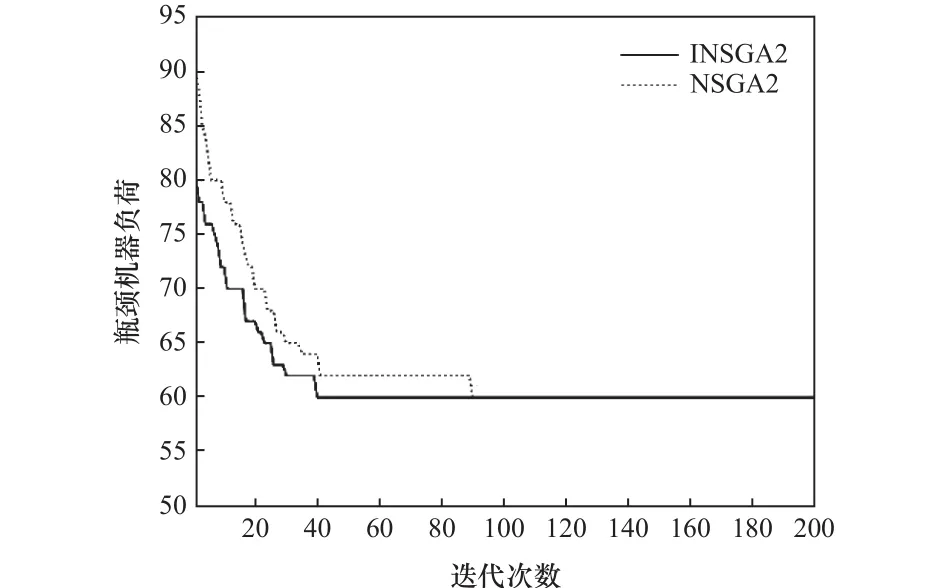
圖9 INSGA-II和NSGA-II瓶頸機器負荷進化過程

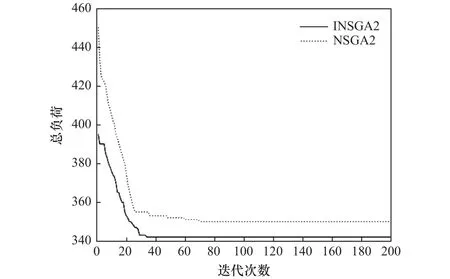
圖10 INSGA-II和NSGA-II總負荷進化過程

3.3 多目標優化算法對比實驗

為了進一步驗證本文INSGA-II算法性能，針對Kacem提出的 8×8，10×10和 15×10這 3個基準算例進行測試，并與Alzahrani J S[13]提出的搶占式約束規則（pre-emptive constraint procedure，PCP）算法，Soto C[14]提出的多目標分支界定算法 （multiobjective branch and bound，MBB）以及 NSGA-II進行對比。優化的目標函數分別為最小化最大完工時間F1，最小化瓶頸機器負荷F2，最小化總負荷F3，算例的結果對比如表3所示。

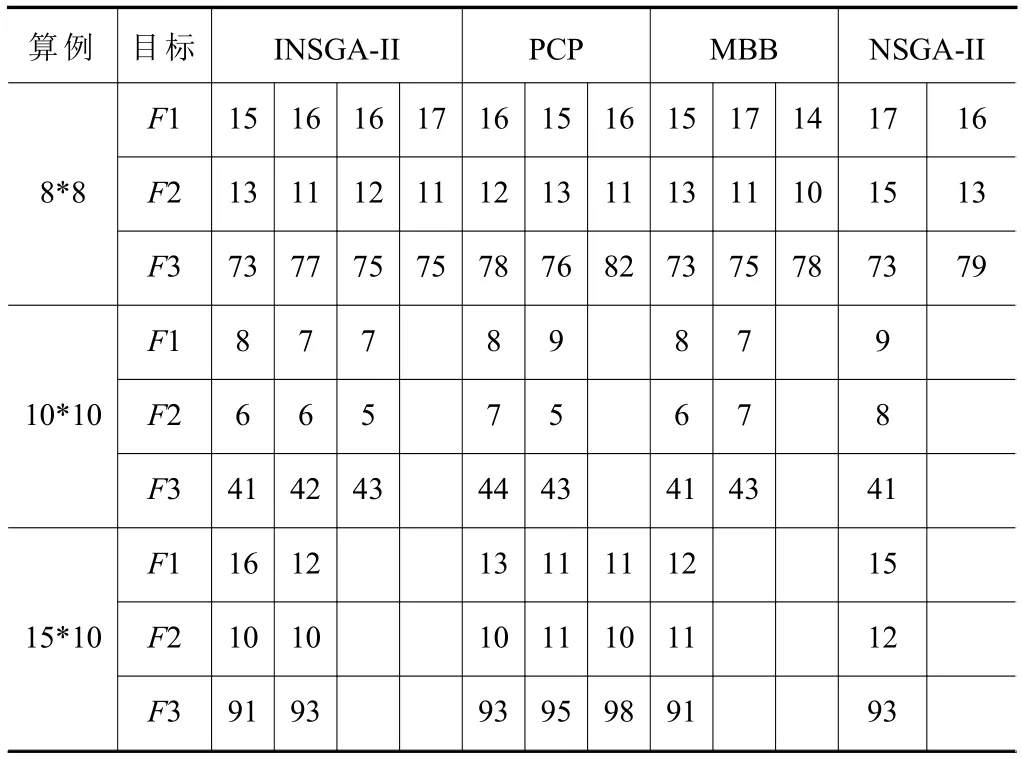
表3 Kacem算例結果對比表

由表中的數據可知INSGA-II算法在求解8*8的算例時得到的非支配解個數為4，多于PCP的3個和MBB的3個以及NSGA-II的2個，且分析數據可知[15,13,73]，[16,12,75]都比PCP的解集[15,13,76]，[16,12,78]更加好。在10×10的算例上，INSGA-II求得的非支配解數量均多于PCP以及MBB和NSGA-II，在15×10的算例上INSGA-II求得的非支配解個數少于PCP的3個，多于MBB和NSGA-II的1個。分析可知，INSGA-II算法能夠有效的求解不同規模的多目標優化問題，并得到質量較高的解集。

3.4 優化調度方案決策分析

在MK04數據集測試，由于該數據集不包含能耗信息，故采用計算機隨機生成數字的方式，添加機器的空載能耗和加工能耗。10個加工機器的空載能耗和機器能耗在[0.1,0.3]和[0.5,2]的范圍內自動生成。生成的數字分別為[0.2,0.1,0.1,0.3,0.2,0.3,0.3,0.2,0.2]，[1.3,0.9,1.7,1.1,1.2,1.9,0.7,0.5]。采用INS-GAII算法優化3個目標函數，即最小化最大完工時間f1，最小化總負荷f2和最小化能耗f3。表3為運行中生成的24個非支配解。

生產決策過程之中，3個指標之間的權重有所差別。由于3個決策目標的值具有不同的量綱，需要將其歸一化：

然后歸一化的目標函數乘以相應的權重系數進行加權求和得到加權的目標函數：

假設決策者對環境指標要求比較高，希望獲得環境友好型的決策，選取的權重系數矩陣W=[0.25,0.25,0.5]，計算得到的最優解目標函數如表4第22條所示，其最大完工時間為86，機器總負載為342，總能耗為390.2，加工信息甘特圖如圖11所示。

圖11 環境友好型決策調度甘特圖

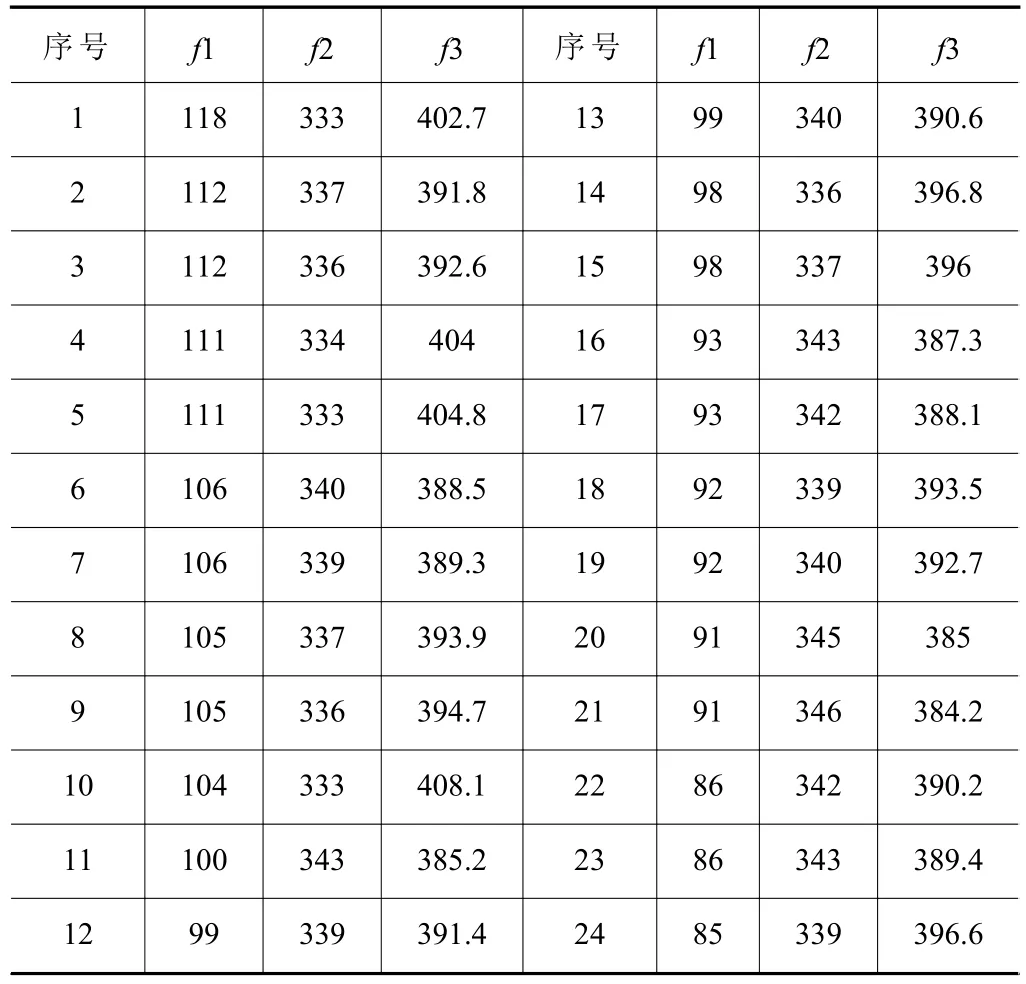
表4 MK04算例Pareto最優解集表

4 結語

本文建立了以最小化最大完工時間、最小化機器負荷、最小化總能耗為優化目標的綠色柔性作業車間調度問題模型。為了有效的求解該問題模型，提出了一種改進的NSGA-II算法，設計了一種非支配的初始化策略，并采用插入式的貪婪解碼策略進行解碼。采用自適應交叉變異算子，結合IPOX交叉和MPX交叉的混合交叉方式，倒序變異和單點最小加工時間突變的混合變異方式，提高算法的搜索能力。針對傳統NSGA-II解集多樣性差、質量低的問題，設計了基于分布函數的改進式精英保留策略，并通過引入一種基于最優解的學習機制來增強算法的局部搜索能力。最后，通過兩個基準測試算例對算法的性能進行了測試，并進行了決策分析，結果表明算法求解多目標優化問題的有效性。

未來研究將考慮不確定環境下的柔性作業車間調度問題，繼續探索多目標優化算法的改進策略，提高算法求解的質量和效率。