機器人攝像機系統標定自動化和誤差評估

席曉亮，楊 洋，程 勇，陸 坤

(1.中國科學院等離子體物理研究所，合肥 230031；2.中國科學技術大學，合肥 230026)

0 引言

隨著機器人在工業范圍的普及，一系列具有機器視覺感知功能的智能機器人把工業自動化帶到了一個新的高度，視覺技術已廣泛應用于機器人領域研究，如實時定位[1]，視覺伺服[2]，控制[3]和校準[4]。在這類機器視覺應用到機器人過程中，視覺傳感器相對于機械臂的手眼關系的標定十分重要，即手眼關系的標定是實現機械臂視覺引導和物體抓取的重要基礎。

Tsai和Lenz提出了兩步法的手眼關系標定法，將旋轉矩陣和平移向量進行分步求解[5]；Ma提出了共同標定法，但系統的精度無法得到保證[6]；Ruda提出了基于四元數工具用非線性優化的工具求解手眼關系[7]；也有文獻中提出了基于最大似然估計的非線性手眼標定方法[8]。非線性手眼標定法相對復雜，實用性較弱。

在傳統的手眼標定中，一般人工給機器人擺位姿，然后人工判斷當前位姿下攝像機采集的圖像是否有效，如果有效抓取當前位姿下的圖像，然后再去擺下一個位姿。一旦發生手眼關系意外變動的情況，如連接件松動、鏡頭損壞、焦距調整等，就需要重新人工標定手眼關系，效率較低。采用人工拖拽法，過程枯燥繁復效率低[9]；手眼關系自動化標定的實現原型，通常結果誤差較大[10]；而發展標定姿態自動生成的算法，會帶來的各種噪聲很大程度影響了標定結果[11]。因此，研究一種可靠、精準的手眼關系自動化標定算法很有必要。

在本文中，對Eye-in-Hand系統提出一種手眼標定算法。在人工拖拽獲得初始手眼關系的基礎上，建立空間姿態約束模型，生成等分空間的位姿點，引入誤差評估機制，對異常樣本進行剔除。實驗表明，引入異常值剔除后，能夠有效減少收斂所需的樣本數量和提升標定精度：平移誤差穩定在0.4mm，旋轉角度誤差最終穩定在0.0018rad。

1 手眼關系標定過程

1.1 標定算法實現過程

手眼關系的自動化標定涉及到圖像位姿檢測、機械臂運動等諸多功能模塊，具體的標定框架過程如圖1所示。UR5驅動、相機驅動以及場景描述文件事先準備完成，相機內參標定采用張正友單平面棋盤格的相機標定法。人工拖拽機械臂四次，確保在機械臂對應位姿情況下，能夠從相機獲取的圖像中計算出marker相對于相機的位姿信息，通過以上四個標定樣本計算得到手眼的初始關系，從而得到marker相對于機械臂基座的初始位姿關系。在初始手眼關系的基礎上，結合空間約束條件，生成相機將要跟隨的等分空間位姿點，然后再轉化為機械臂末端在機器人基座坐標系下要跟隨的位姿點，通過RobWork進行路徑規劃，當機械臂到達相應位姿點后，判斷當前相機視野是否可以計算出marker的位姿，如果可以，就將這組marker位姿和對應的機器人關節位姿存入標定樣本集中去計算，否則繼續下一個位姿點的跟隨。最終通過循環計算，得出標定結果。

圖1 算法實現過程

1.2 等分空間約束的位姿生成

手眼關系的自動化標定，離不開可行位姿點的生成。文獻[5]中指出提高手眼標定精度的四個重要準則：

1）盡可能增大相對運動旋轉軸之間的夾角；

2）盡可能增大相對運動的旋轉角度；

3）盡可能減小標定板到相機光軸中心的距離；

4）盡可能減小末端在不同姿態之間的距離。

基于這些準則，以marker的中心為原點建立球坐標系，合理約束相機坐標系原點到球坐標系原點的距離r，以及相機光軸與z軸夾角θ。設定相機坐標系原點到marker中心最小距離rmin=0.2m最大距離rmax=0.38m，夾角θmin=0，θmmax=π/6，在xoy平面與x軸的夾角αmin=0，αmax=2π。

為了保證采樣點在空間中的均勻分布，在采樣過程中在約束的范圍內對α,θ,r進行等分采樣。為了確定(α,θ,r)位置處相機的姿態，定義相機的光軸指向球坐標原點的徑向方向，相機光軸作為在該位置點處的zc軸，然后定義相機的xc與yc，具體如如圖2所示。xc垂直于面OcOF，從而確定在該位置點處相機的方向信息，最終作為相機將跟隨的一個位姿點。依據圖2的示意圖，可以得到位姿點處的笛卡爾坐標系相對于以marker中心為坐標系的笛卡爾坐標系的旋轉矩陣和平移矩陣分別為：

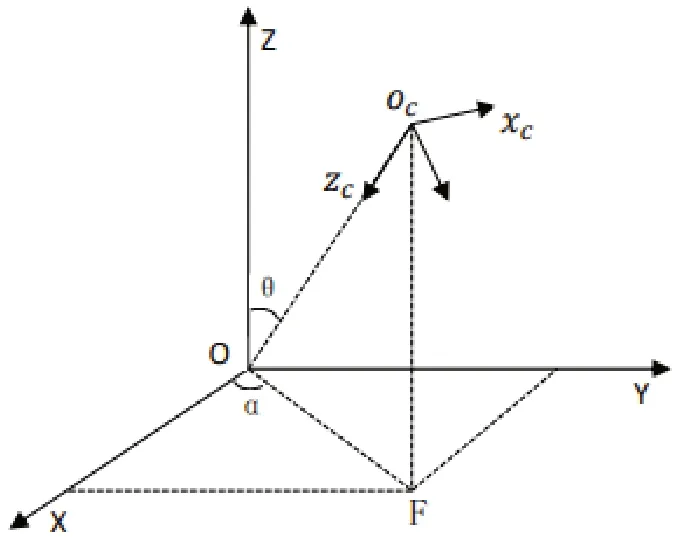
圖2 空間約束模型原理圖

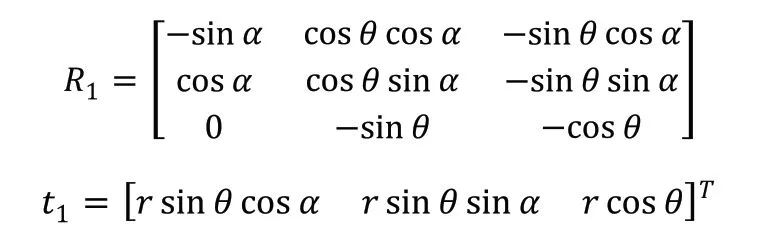
[R1丨t1]構成了生成位姿點的位置和姿態，基于手眼初始關系和[R1丨t1]可以得到生成的采樣點在機械臂基座坐標系下的位姿，從而下一步基于RobWork對機器人進行采樣點跟隨的運動，使得機器人末端的相機到達預期位姿。

2 手眼關系標定原理

2.1 Tsai-Lenz 標定計算

Tsai-Lenz是一種計算機械臂末端坐標系與相機坐標系間手眼關系的算法。需要的數據有機械臂末端坐標系之間相對位姿變換矩陣、攝像機坐標系間的相對位姿變換矩陣。相機安裝在機械臂上，并在相機視野內放置marker，則有以下變換矩陣關系[12]：

根據上述的變換矩陣關系式，可以得到：

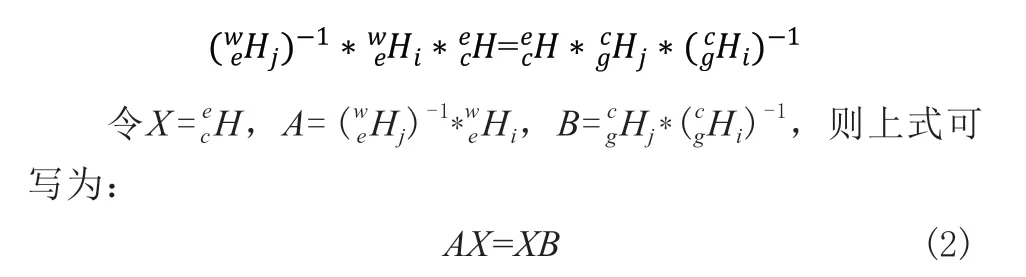
在AX=XB求解中，至少需要兩組A、B才能計算出結果，也就是至少需要采集3個標定樣本。實際標定過程，需要采集更多的標定樣本，來獲得更好的標定精度。

2.2 pnp圖像位姿求解原理

在本實驗中，marker是一個平面，且marker的真實方塊物理尺寸是已知的，這些角點在相機中的像素坐標也是已知的。對于DLT解法，場景中角點P的齊次坐標P=(x,y,z,1)，齊次化表示其在像素平面上對應的投影特征p=(u1,v1,1)點，s表示尺度因子。記增廣矩陣[R丨t]是3*4的矩陣，即：

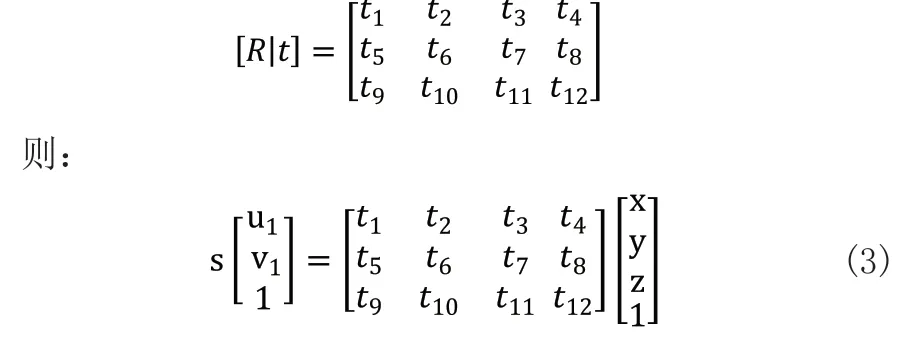
用式(3)最后一行把s消去，得到兩個約束[13]：

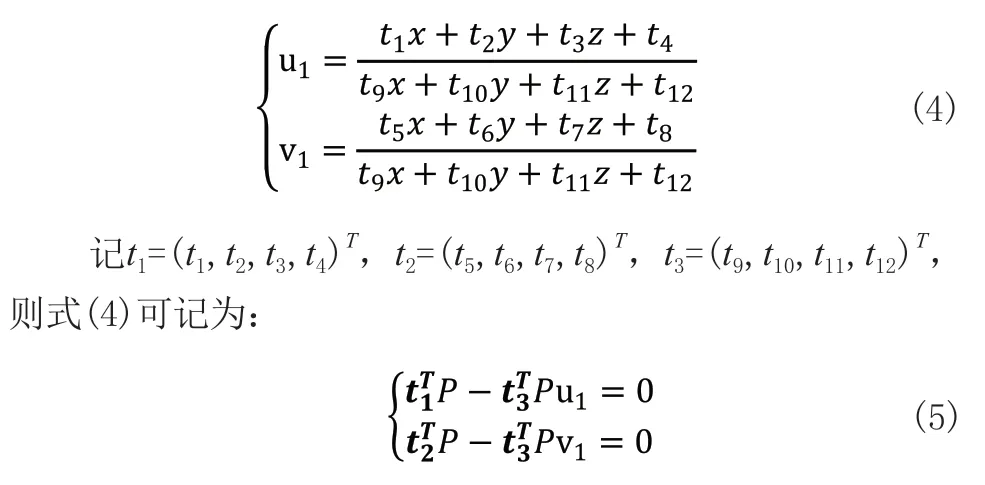
每個特征點提供了關于t(t1,t2,t3)的兩個線性約束，對于3*4的[R丨t]矩陣，6對匹配點即可求得求解相機與marker間的[R丨t]矩陣，即位姿矩陣。攝相機在某采樣點拍攝照片如圖3中左圖所示，采用棋盤圖檢測法對左圖進行內角點檢測并按角點編號順序連接，得到圖3中右圖。基于檢測到的內角點，下一步使用上文所述的pnp算法求解。

圖3 棋盤圖在攝像機坐標系中的位姿求解

2.3 誤差評估機制

手眼標定結果的精度直接取決于所獲取計算數據的準確性。OpenCV棋盤圖檢測時，會存在有些圖像因為光線等問題給圖像帶來噪聲干擾[14]，導致個別圖像計算出來的位姿出現很大誤差，如果把這種異常樣本放在后續的計算循環中，則會導致后面每一次更新計算出來的結果都會相應的產生較大誤差，因此，在每次更新計算前，需要對新的圖像位姿數據進行誤差評估，如果是非異常值則添加入計算數據中進行當次的更新計算。

對于非異常值的圖像計算序列chessPosem和對應的機械臂位姿計算序列tcpPosem(m=1,2,...,i,...n)，對應于前n組計算序列的得到的結果Rx和tx，按照參考文獻[15]定義，(k=1,2,...,j,...n-1)。從E1到Ej服從正態分布的特征，求得其正態分布的均值mean和方差stdev。對于i+1第組的計算樣本，定義允許的誤差區間[floor,ceiling]：

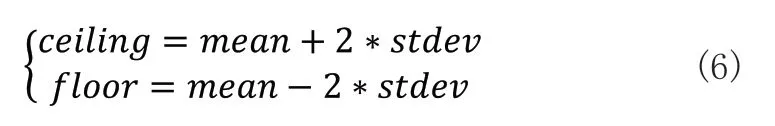
當機械臂運行到下一個有效位姿點時，記錄在這個位姿處的chessPosei+1和tcpPosei+1，結合tcpPosei和chessPosei，計算得到Ej+1：

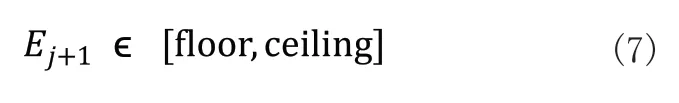
如果Ej+1滿足條件(7)則把chessPosei+1和tcpPosei+1放入非異常值計算序列中，然后更新計算序列的誤差區間[floor,ceiling]。如果Ej+1不滿足條件(8)則認為chessPosei+1和tcpPosei+1是異常值，不放入非異常值計算序列中。接下來對下一個位姿點處的圖像位姿數據和機械臂位姿數據同樣按照這樣去判定。

3 實驗部分

機器人手眼標定實驗在Ubuntu18.04操作系統下基于ROS搭建，采用OpenCV進行圖像處理。RobWork是一個用于仿真模擬控制機器人的平臺，能夠和ROS很好的集成。

3.1 仿真實驗

基于RobWork搭建仿真實驗平臺，添加虛擬相機獲取圖像信息。仿真實驗平臺如圖4所示。按照如圖1所示的算法實現流程開展實驗。

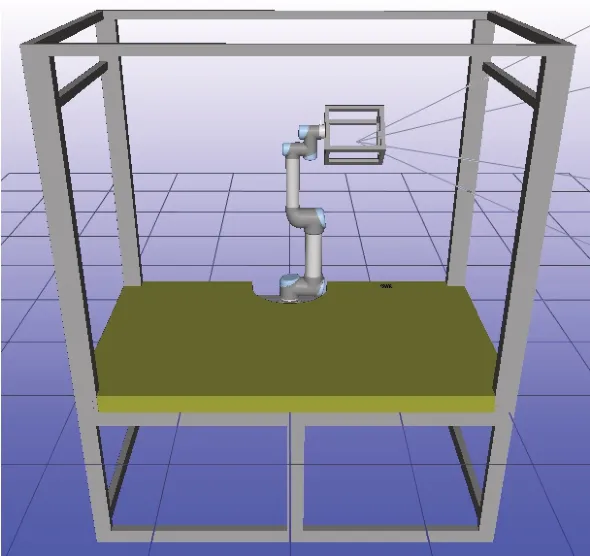
圖4 仿真實驗平臺

基于α,θ,r的范圍約束[16]，采用等空間采樣法，生成采樣位姿點。在循環更新計算部分，當計算序列在4組及以上時開始計算，然后每到一個有效位姿點，就把該位姿處對應的圖像位姿和機械臂位姿數據放入計算序列中，和之前的計算序列一起計算更新當前位姿下的手眼關系。tn、Rn定義用n組數據更新計算得到的平移矩陣和旋轉矩陣。ttrue、Rtrue定義手眼關系的平移矩陣真值和旋轉矩陣真值，可以直接從仿真環境配置文件中讀出。

位置誤差的定義由更新計算得來的平移向量與真值平移向量做差取模得出[17]：

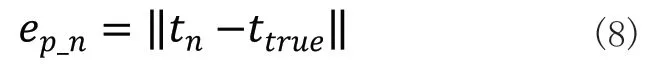
角度誤差的定義由計算得來的旋轉矩陣與真值旋轉矩陣的轉置相乘后的結果通過羅德里格斯公式處理為旋轉向量，再取模得出：

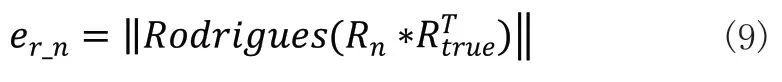
對應的ep_n、er_n曲線分別如圖5、圖6所示。

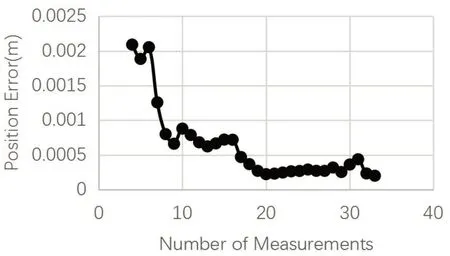
圖5 仿真實驗位置誤差曲線

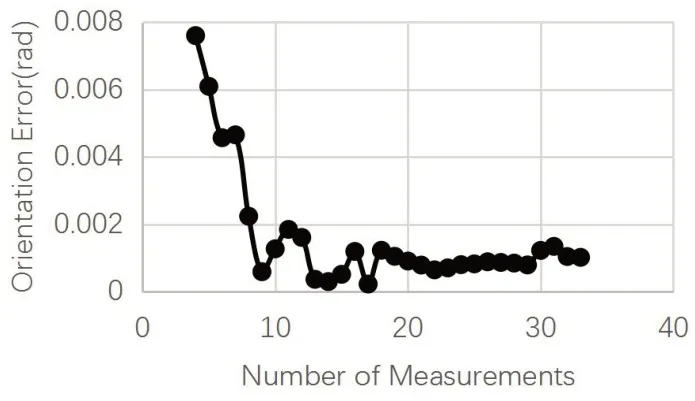
圖6 仿真實驗旋轉角度誤差曲線

圖5橫軸代表每次計算時所采用的計算樣本數，縱軸代表對應序列數下所得值與真值的誤差，位置誤差曲線隨著計算序列組迭代更新而整體持續下降，最終在第22次更新后達到0.2mm左右的穩定收斂狀態。圖6旋轉誤差呈現下降趨勢，最終在第22次的更新后達到0.0008rad左右的收斂狀態。

3.2 實體實驗

本論文的實體實驗平臺如圖7所示。采用UR5協作機器人末端搭載Stingray F504 CCD相機。通過ROS平臺建立機器人、攝像機和標定程序之間通訊和控制網絡。

圖7 實體實驗平臺

依據Tsai-Lenz兩步法求解方程AX=XB，至少需要兩組的A和B才能得出一個初始的X結果。此處和的初始A和B計算樣本數從4開始，機械臂每到一個采集點進行相機拍照，如果圖像可以計算出位姿，則把當前的圖像位姿信息和機械臂位姿信息和前面4組對應信息一起作為下一次更新計算手眼關系的數據。如果采集點機械臂不可達或機械臂到達后，相機圖像不能計算出圖像的位姿，則該位姿點跳過，繼續進入到下一個位姿點處的相關計算流程。每一個位姿點處的X更新計算完后，計算當次計算結果的位置誤差與旋轉誤差。實體實驗中ep_n、er_n和式(8)、式(9)定義一致，得到對應的ep_n、er_n曲線如圖8、圖9所示。對130個標定采集樣本，每次隨機采樣80組用于計算出一個t、R，總共取50次，最后對這50個t、R分別取均值，得出ttrue、Rtrue。

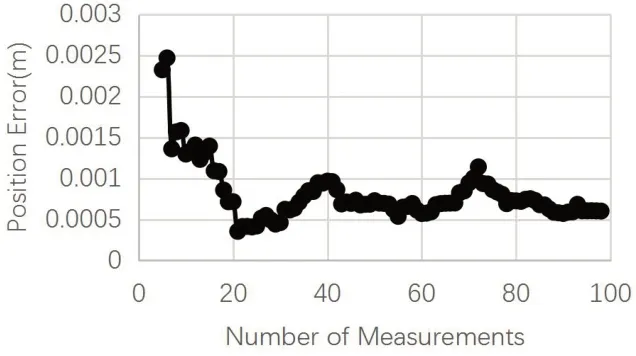
圖8 實體實驗位置誤差曲線

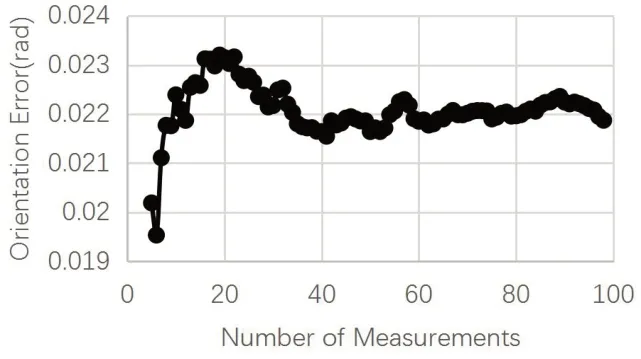
圖9 實體實驗旋轉角度誤差曲線

實體實驗使用固定焦距的CCD相機，相較于仿真環境，采集到的圖像不可避免會存在瑕疵，前一次迭代樣本中存在的誤差會一直在后續計算組中去計算。在第65組新后，位置誤差在0.6mm左右，旋轉誤差在0.0224rad左右。采集樣本中的異常點，會導致標定誤差波動，但隨著樣本數的增加，誤差的波動范圍降低了。

3.3 引入異常值剔除環節

在實體實驗中引入誤差評估機制，按照式(6)、式(7)對異常值進行剔除。每次非異常值計算序列更新后，計算得到一個對應于該組計算序列的手眼標定值，并依據式(8)、式(9)得到ep_n、er_n。得出的位置誤差曲線如圖10、圖11所示。

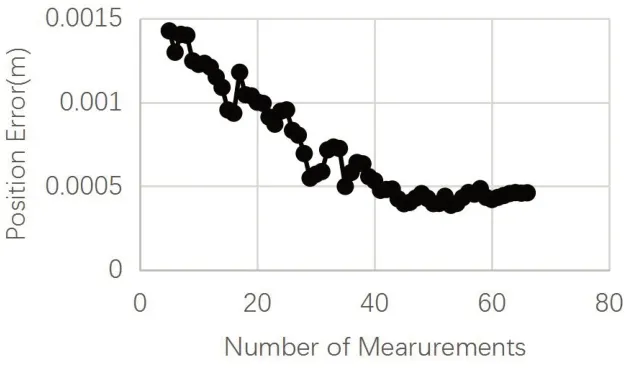
圖10 異常值剔除后的實體實驗位置誤差曲線

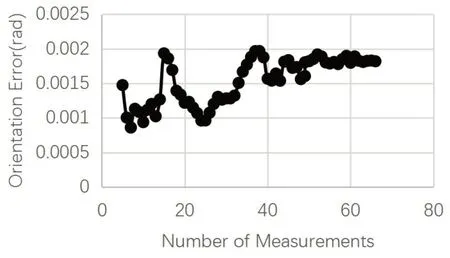
圖11 異常值剔除后的實體實驗角度誤差曲線

從圖10所示位置誤差曲線中可以看出，引入異常值剔除環節后，當計算組更新到45組時已經趨于穩定，位置誤差最終穩定在0.4mm左右，而且位置誤差從始至終在極小的范圍內波動（約為0.1mm）。相對于無異常剔除機制的測試結果：第65迭代達到的0.6mm位置誤差，異常值剔除環節引入后在收斂速度和誤差精度方面都起到了明顯的優化效果，而且誤差穩定了，不會出現大幅度波動的情況。

圖11中所示的旋轉誤差曲線，計算更新到第45組時已經趨于收斂，旋轉角度誤差最終穩定在0.0018rad左右，引入誤差剔除前的測試結果：第65組時角度誤差穩定在0.0224rad，在計算速度和精度上都有了顯著提升，而且旋轉誤差全程的波動范圍在0.0012rad以內。

位置誤差和旋轉誤差在更新中都存在微小的震蕩，這是因為異常值判定標準當中的誤差判定區間是[mean+2*stdev,mean-2*stdev]，對應于2倍標準差的區間，其置信概率是95.5%，這會導致有些誤差較大但在判定區間內的序列也會被計入計算序列中，從而導致下次的異常值誤差判定區間的范圍又變大，而在更新計算環節中，當次加進來的計算序列也會在接下來的更新輪次中反復用于計算。如果把誤差判定區間設置的較小，會導致對應的置信概率會比較小。

3.4 與主流方法的比較

現有主流的方法有NAVY算法（Park[18]）、INRIA算法（Horaud[19]）、對偶四元數算法（Daniilidis[20]）。依據式(8)、式(9)所定義的ep_n、er_n，采用現有主流方法進行計算，得出標定的位置誤差和角度誤差。NAVY算法（Park）的位置誤差和角度誤差結果分別如圖12、圖13所示。

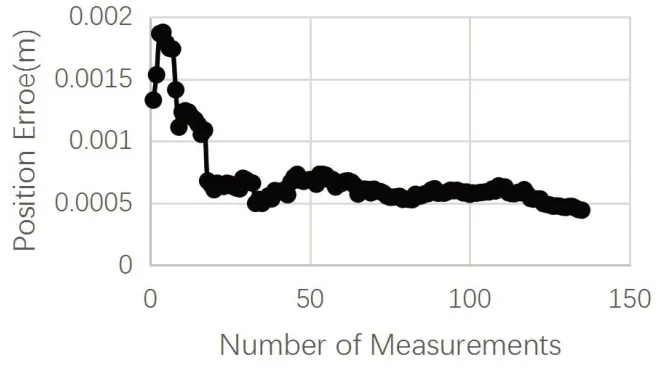
圖12 NAVY算法位置誤差曲線

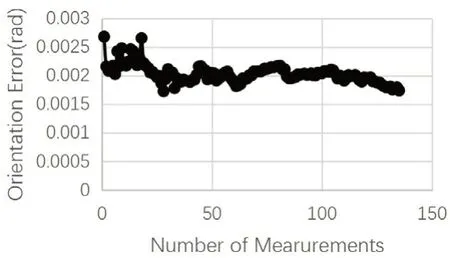
圖13 NAVY算法角度誤差曲線

從圖1 2 可以看出，在8 5 次更新后，位置誤差在0.529mm左右，角度誤差在0.002114rad左右。對接下來的兩種主流方法分別開展實驗，發現這兩種方法和INRIA算法得出的誤差曲線趨勢基本一致。

把仿真實驗結果、實體實驗結果、引入異常值剔除環節后的實驗結果、主流方法結果整理如表1所示。

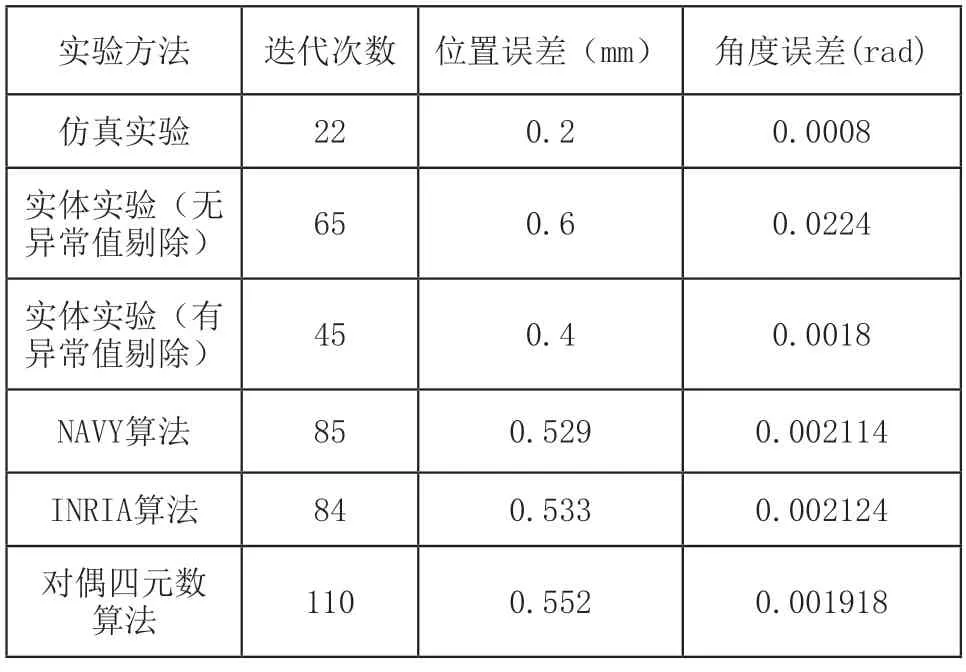
表1 標定仿真和實體實驗結果匯總

表1中三種主流方法得到的實驗結果基本一致。發現主流方法在位置誤差和角度誤差上優于實體實驗（無異常值剔除）的結果。加入異常值剔除算法后，位置誤差和角度誤差結果優于主流方法。

在引入異常值剔除環節后，在標定計算精度和迭代次數上相對于表一中的其它方法有了較大提升，說明了該算法的有效性與優越性。

4 結語

本文提出了一種機器人手眼自動化標定的算法。首先人工拖拽機器人4個位姿，得出初始的手眼關系。在初始手眼關系的基礎上，建立基于maker的等分空間位姿約束模型。機械臂對這些位姿進行逐一跟隨，采集標定樣本，基于Tsai-Lenz方法完成循環更新計算。在每一次更新計算完成后，計算當次的位置誤差和旋轉角度誤差。

在仿真實驗中，干擾因素較少，位置誤差在第22組的更新后達到0.2mm左右的穩定收斂狀態，旋轉角度誤差在第22組的更新后達到0.008rad左右的收斂狀態。實體實驗中，位置誤差在第65組的更新后達到0.6mm左右，轉角度誤差在第65組的更新后達到0.0224rad左右，后續的樣本中有異常出現，導致標定誤差波動。針對這種情況，提出了誤差評估機制，對異常計算序列進行剔除。加入異常值剔除環節后，位置誤差在第45組的更新后達到0.4mm左右的穩定收斂狀態，旋轉角度誤差在第45組的更新后達到0.0024rad左右的收斂狀態。最后用三種主流方法進行實驗，發現主流方法標定的位置誤差和角度誤差結果介于兩者之間，說明了異常值剔除環節的有效性與優越性。