不平衡負載下四橋臂逆變器的積分滑模控制

喬 和，楊涵杰

（遼寧工程技術大學 電氣與控制工程學院，葫蘆島 125105）

0 引言

近年來，分布式發電技術以充分利用各種可再生能源、高可靠性、低污染的優點迅速發展，多種分布式電源以微網的形式接入大電網，憑借可靠靈活的運行特點引起廣泛關注[1～4]。離網模式下的微網要求對分布式電源進行協調控制，保證電網失去外部供電或出現故障時對重要負荷的持續供電。離網運行時微網所需的負載功率主要由逆變器電源所供給，交流負荷里含有大量單相與三相負載易導致輸出電壓不平衡，對微電網系統的穩定性造成嚴重影響，所以進行不平衡負載下逆變器控制的研究極其重要[5～7]。

三相四橋臂逆變器具有結構簡單、體積小和直流電源轉化率高等優點，為了保證其在不平衡負載下的有效運行，采取了許多控制方法。傳統的比例積分控制器（Proportion Integral，PI）簡單易實現，通常用于在dq坐標系下跟蹤恒定參考信號，但系統整體性能會受到參數攝動和負荷變化的影響，盡管采用正負序分離的方法能夠改善性能，但是增大了計算負擔[8]；比例諧振（Proportion Resonant，PR）控制器可用于abc和αβ坐標系并實現零穩態誤差，但對頻率變化敏感，會降低系統的整體性能[9]；模型預測控制（MPC）和無差拍控制（DBC）方法具有快速的動態響應特性，但均需要精確的數學模型，對模型參數失配的敏感性較高，且模型預測控制需要為所有可用電壓矢量計算成本函數，給四橋臂逆變器帶來很大的計算負擔[10]。

滑模控制（Sliding Model Control，SMC）的不連續性與逆變器的變結構特點相符，適合采用閉環控制的逆變器。文獻[11～13]研究了單相和三相逆變器的滑模控制器，保證在線性和非線性負載情況下，輸出電壓的總諧波失真均較小，但存在輸出電壓抖振較大的問題；文獻[14,15]針對三相逆變器，提出了基于狀態空間方程的積分滑模控制器，抑制了輸出電壓的高頻抖振且對外部干擾具有較強的魯棒性，但模型推導較為復雜。本文提出一種四橋臂逆變器的積分型滑模控制器，保證逆變器在不平衡負載下輸出電壓的高度對稱性。首先利用矢量控制建立dq0旋轉坐標系下的數學模型，然后構建系統狀態的積分滑模面，給出了控制律的詳細推導過程；并采用李雅普諾夫函數穩定性理論驗證了系統的穩定性；最后通過仿真與PI控制器進行對比，驗證了所提控制器的正確性和有效性。

1 三相四橋臂逆變器模型

三相四橋臂逆變器的拓撲結構如圖1所示，其中Vdc為直流電源電壓，va、vb、vc、vn為四橋臂所對應的電壓，ila、ilb、ilc為三相電感電流，iln為中性線補償電流，L為濾波電感，C為濾波電容，vAG、vBG、vCG為三相負載電壓，ia、ib、ic為三相負載電流，Za、Zb、Zc為三相負載阻抗。

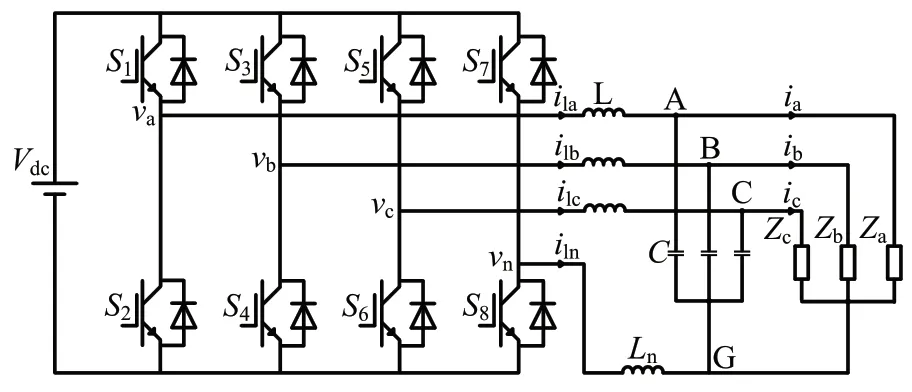
圖1 三相四橋臂逆變器拓撲

設da、db、dc、dn為四橋臂導通比，n為母線中點電位，可得三相四橋臂輸出電壓van、vbn、vcn為：

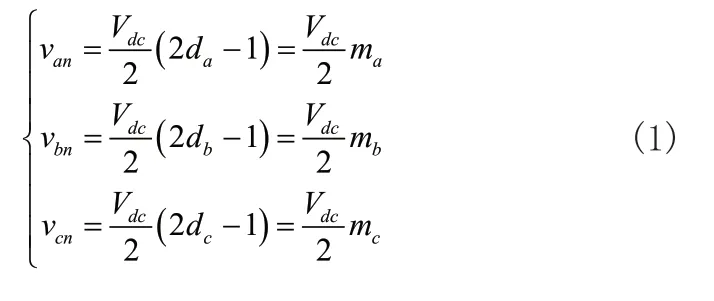
其中，mx=2da-1，x=a、b、c。

根據基爾霍夫電壓和電流定律，四橋臂逆變器系統中各量之間存在如下關系：

其中r和rn分別為濾波電感L和中線電感Ln的寄生電阻。

dq0旋轉坐標系由abc靜止坐標系逆時針旋轉ω后得到，由矢量合成原則可得變換關系為：

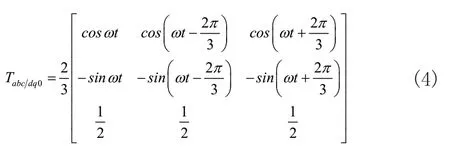
式(2)和式(3)對應旋轉坐標系dq0的模型為：

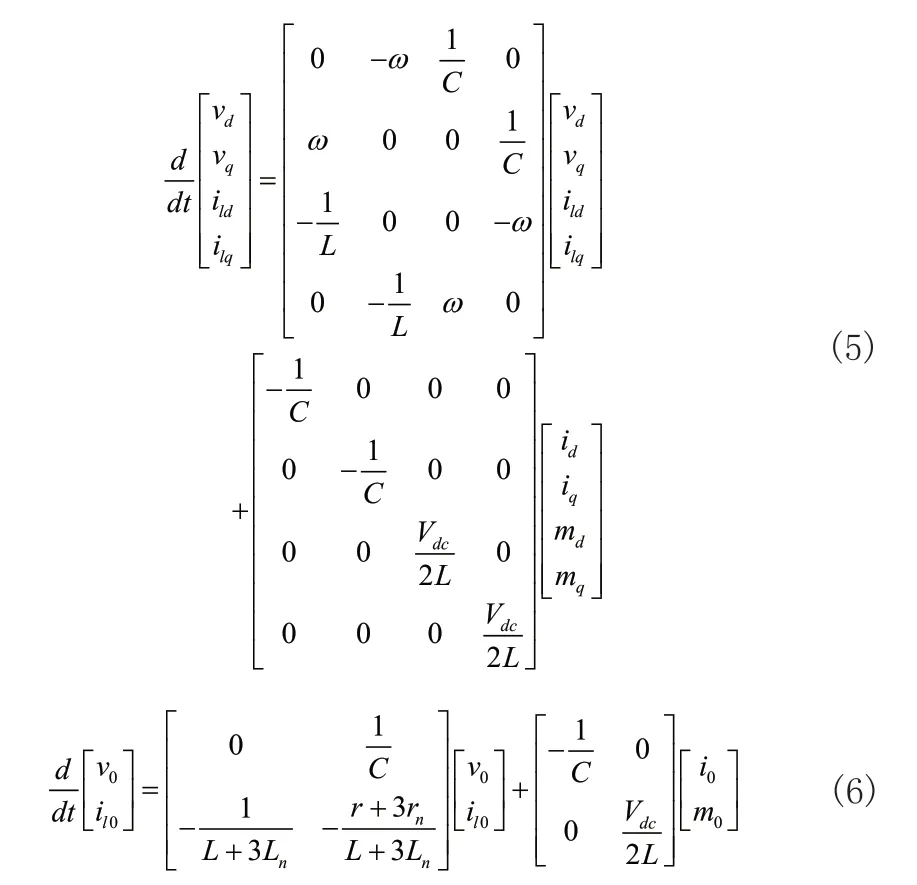
由式(5)和式(6)可得四橋臂逆變器的系統模型為：

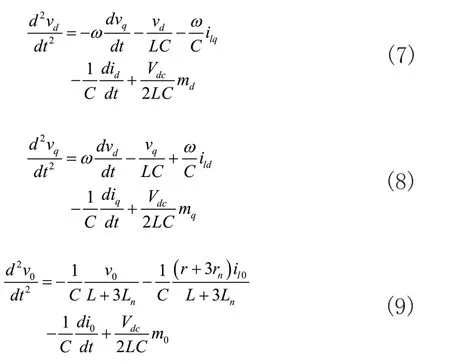
2 積分型滑模控制器

2.1 控制器設計

積分型滑模控制器的設計是定義一個良好的滑模面和控制律，為了方便計算，首先簡化四橋臂逆變器的系統模型可得：

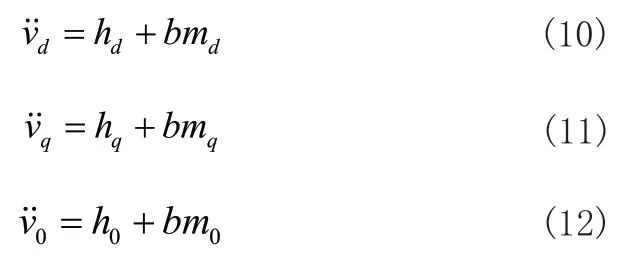
其中：

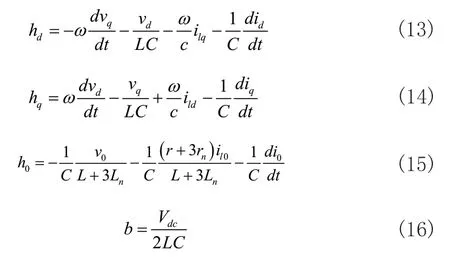
為了實現滑模控制，通常利用跟蹤誤差作為狀態變量，由此定義滑模控制的輸入量為：

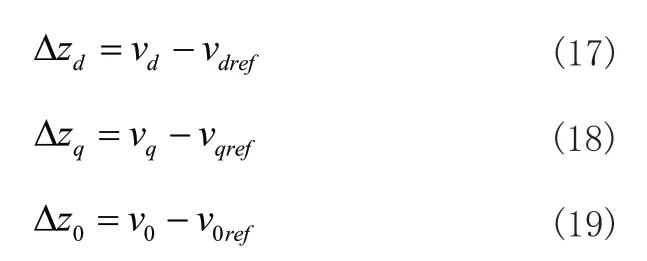
其中vdref、vqref、v0ref分別為d、q、0軸的參考電壓。

為了消除控制器中被跟蹤信號的導數項，在傳統滑模面設計的基礎上，引入跟蹤誤差的積分項，構成dq0軸的積分滑模面為：

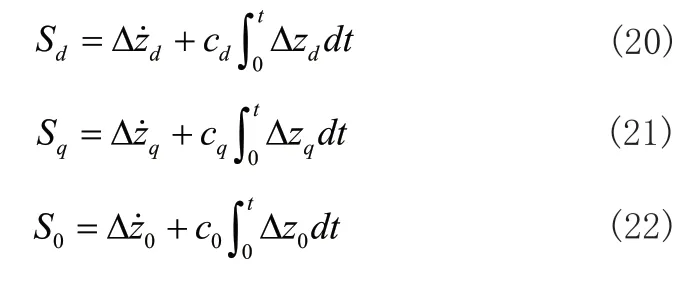
其中cd、cq、c0為設計的滑模面參數。

為了便于后文計算，對dq0軸輸入量求二階導并分別代入到式(20)～式(22)的一階導數中可得：

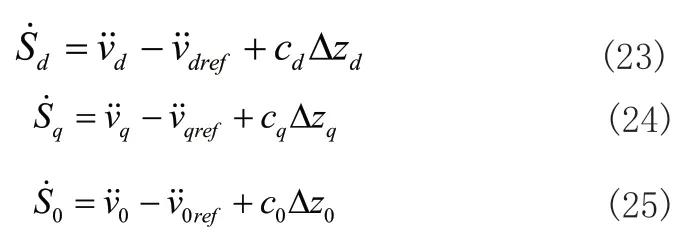
由于參考電壓往往設定為常數，dq0軸參考電壓的二階導數為零，并將簡化的四橋臂逆變器系統模型代入式(23)～式(25)中可得：

其中k表示趨近于滑模面的速度，kd＞0、kq＞0、k0＞0為積分滑模控制器常數，sgn(·)為符號函數，表示為：

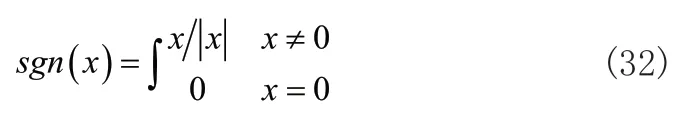
2.2 穩定性分析

為了保證四橋臂逆變器系統的穩定性，定義李雅普諾夫函數：

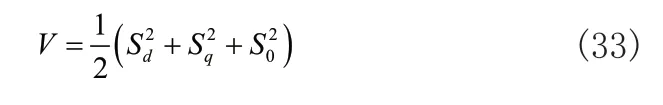
從定義的Lyaponov函數可以看出，函數V在除了原點之外的所有值均大于零，將設計的控制律代入到式(33)的一階導數中可得：

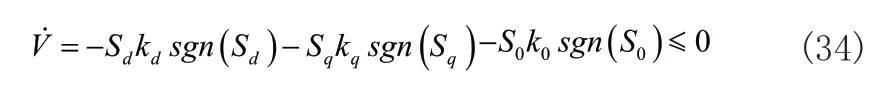
結合結論V≥0可知，該系統滿足李雅普諾夫穩定性定理，可以認為此系統是漸近穩定的。

3 仿真結果分析

為了驗證積分滑模控制器的性能，在MATLAB/Simulink中進行負荷和系統參數變化的仿真。系統參數：直流電源電壓Udc=720V，LC濾波器中L=2mH，C=300μF，寄生電阻R=Rn=0.001Ω，中線電感Ln=440μH，開關頻率fs=20kHz，ω=100rad/s。積分滑模控制器參數：Cd=5，Cq=5，C0=1，Kd=5，Kq=10，K0=2。

當四橋臂逆變器接不平衡阻性負載時，令Za=15Ω，Zb=18Ω，Zc=12Ω，圖2和圖3為兩種控制下逆變器輸出電壓電壓和電流波形圖。經對比可以看出，積分滑模控制下三相電壓付幅值差異較小，在t=0.3s時同時并入5Ω純阻性負載，電流增大且持續時間為0.1s，輸出電壓在受到干擾前后沒有發生明顯變化，仍保持一定的對稱性。

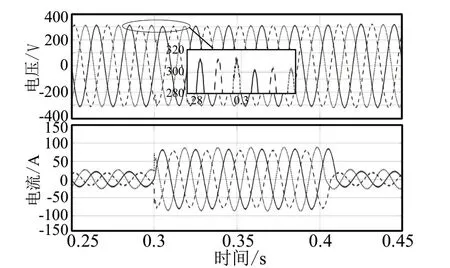
圖2 PI控制下輸出電壓和電流波形圖（不平衡阻性）

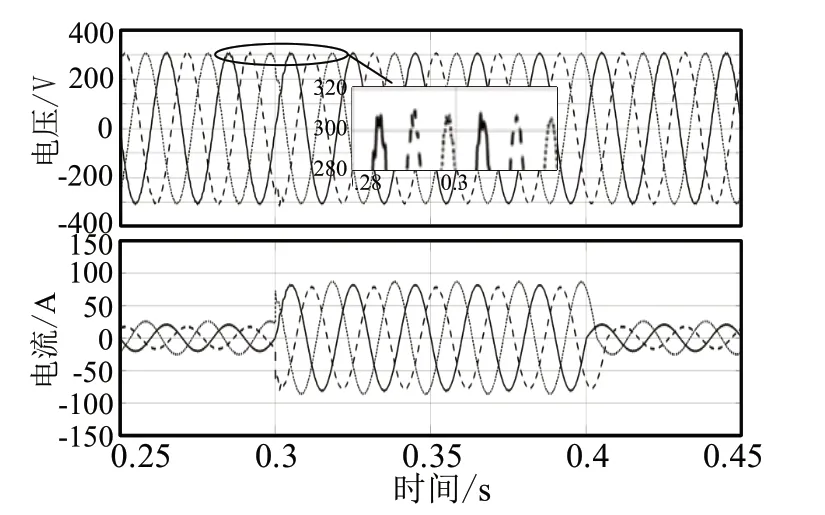
圖3 ISMC控制下輸出電壓和電流波形圖（不平衡容性）

圖3和圖4為四橋臂逆變器接不平衡容性負載時，采用PI控制和積分滑模控制下逆變器的輸出電壓和電流波形圖。

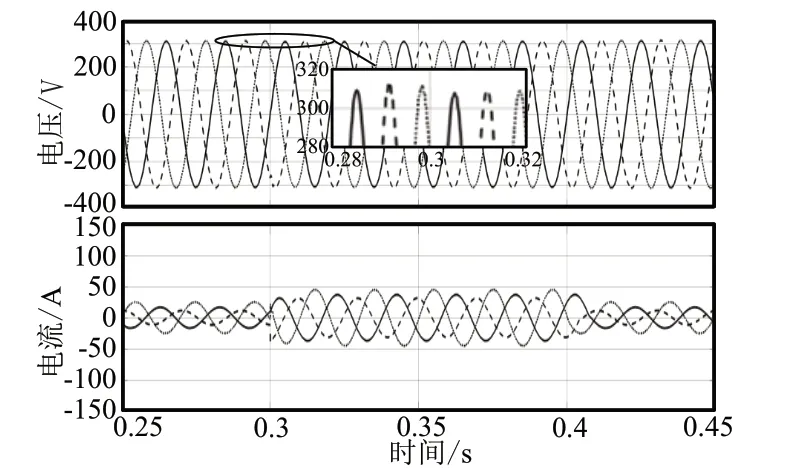
圖4 PI控制下輸出電壓和電流波形圖（不平衡感性）

三相負載分別為：15Ω，290μF；25Ω，300μF；5Ω，280μF，由仿真結果可以看出，積分滑模控制下輸出電壓對稱性較高，在t=0.3時突并10Ω，280μF容性負載，輸出電壓無明顯波動，仍保持較高的對稱性。

當四橋臂逆變器接不平衡感性負載時，圖5和圖6分別為采用PI控制和積分滑模控制下逆變器的輸出電壓和電流波形圖，三相負載分別為：15Ω，10μF；25Ω，15μF；8Ω，5μF，從圖中可以看出，0.3s時突并5Ω，10μF感性負載，當電流發生變化時，積分滑模控制下輸出電壓不隨電流的改變而發生改變。

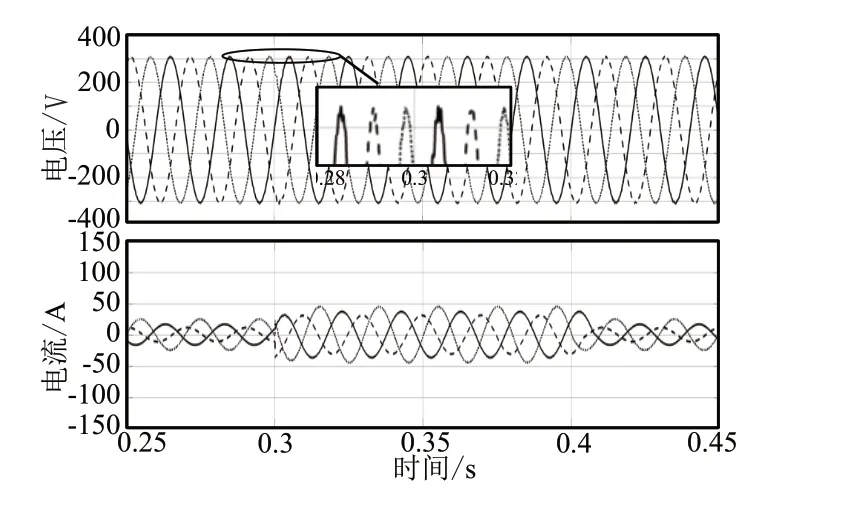
圖5 ISMC控制下輸出電壓和電流波形圖

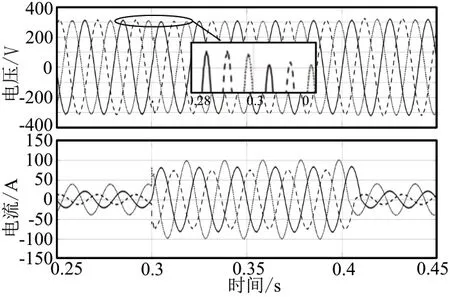
圖6 PI控制下輸出電壓和電流波形圖

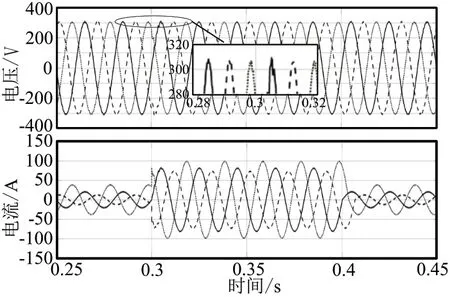
圖7 ISMC控制下輸出電壓和電流波形圖

通過上述三種負載變化的仿真實驗可以看出，積分滑模控制器的控制效果優于傳統PI控制，穩態時三相電壓對稱性較高，負載突變時具有更好的抗干擾能力和較強魯棒性。

圖8為電感變化時逆變器輸出電壓和電流波形圖，在t=0.2s時電感變化為給定值的200%，通過仿真結果可以看出，濾波電感的變化對輸出電壓對稱性幾乎無影響。

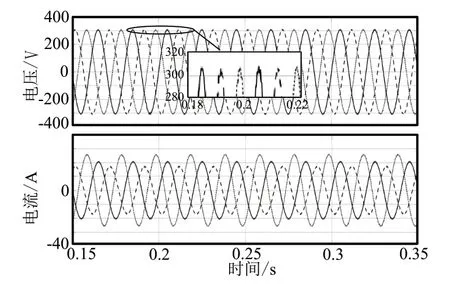
圖8 ISMC控制下電感變化輸出電壓和電流波形圖

4 結語

本文針對四橋臂逆變器在不平衡負載下輸出電壓不平衡的問題，提出了一種基于矢量控制的積分型滑模控制器。推導了四橋臂逆變器系統在dq0旋轉坐標系下的數學模型，并基于此模型結合滑模控制原理給出了控制器設計的詳細過程，通過李雅普諾夫函數穩定性理論驗證了系統的穩定性。仿真分析結果表明：所提出的積分型滑模控制器計算量小，能夠消除系統參數攝動帶來的影響；系統輸出電壓穩態精度高同時對于時變的負荷干擾具有良好的動態性能。