LBSO-PID控制方法在工業(yè)控制中的應(yīng)用
彭繼慎,李希桐
(遼寧工程技術(shù)大學(xué) 電氣與控制工程學(xué)院,葫蘆島 125105)
0 引言
PID控制作為一種算法結(jié)構(gòu)簡單且易實(shí)現(xiàn)的控制方法已經(jīng)被廣泛應(yīng)用于各種工業(yè)控制系統(tǒng)中[1]。目前,大多數(shù)工業(yè)控制系統(tǒng)具有大時(shí)階以及非線性的特點(diǎn),為了提高工業(yè)控制效果,需要對影響PID控制效果的比例、積分以及微分三個(gè)參數(shù)進(jìn)行整定選擇[2]。傳統(tǒng)的PID整定方法主要有Z-N法以及工程整定法,但是這兩種方法存在受主觀影響以及計(jì)算量大的問題。隨著人工智能算法的不斷發(fā)展進(jìn)步,且由于基于人工智能算法的PID整定方法的自適應(yīng)能力強(qiáng)且整定效果相對傳統(tǒng)方法優(yōu)良,相關(guān)研究人員提出利用諸如神經(jīng)網(wǎng)絡(luò)、遺傳算法等智能算法對PID三個(gè)參數(shù)進(jìn)行自整定計(jì)算[3~6],但是這些算法大多存在易陷入局部解,迭代收斂速度慢以及求解精度低的問題。
因而為提高PID參數(shù)整定的精度,本文提出一種基于LBSO算法的PID整定方法。該方法結(jié)合了BAS算法的局部求解能力、PSO算法的全局搜索能力,從而有效提高了算法對最優(yōu)解的求解能力,另外,算法結(jié)合了Levy隨機(jī)步長特性,使算法陷入局部解的可能性降低,最后本文通過實(shí)驗(yàn)對所提方法進(jìn)行了驗(yàn)證。
1 PID控制原理
PID控制方法是由比例、積分以及微分環(huán)節(jié)組成的一種控制方法,其中比例環(huán)節(jié)主要控制系統(tǒng)的響應(yīng)速度、積分環(huán)節(jié)主要為了實(shí)現(xiàn)系統(tǒng)的無差調(diào)節(jié),而微分環(huán)節(jié)主要為了減小超調(diào)進(jìn)而改變系統(tǒng)的動態(tài)響應(yīng)性能。其具體控制函數(shù)可由式(1)表示:
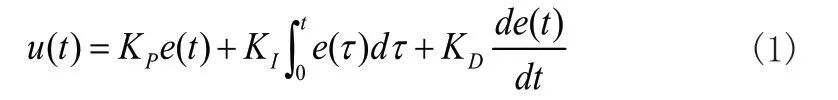
式中,Kp為比例環(huán)節(jié)系數(shù)、Ki為積分環(huán)節(jié)系數(shù)以及Kd為微分環(huán)節(jié)系數(shù)。由此,其傳遞函數(shù)如式(2)所示:
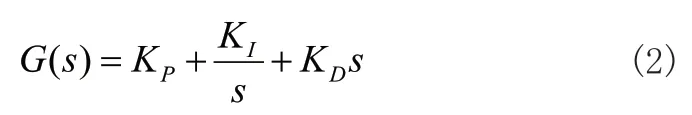
2 LBSO算法建模
有N個(gè)個(gè)體、D維的Levy-BSO算法其個(gè)體可初始化為Xi=(xi1...xii...xiD),那么其群體即可表示為X=(X1...Xi...XN),由于算法參考了PSO算法的群體機(jī)制,因而對于當(dāng)前個(gè)體最優(yōu)位置可用Pi=(Pi1...Pii...PiD)表示,那么群體當(dāng)前最優(yōu)位置便可表示為Pg=(Pg1...Pgi...PgN)。對個(gè)體速度更新計(jì)算如式(3)所示[7]:
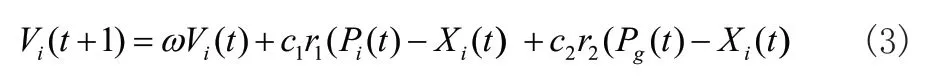
其中ω為算法慣性權(quán)重因子,為權(quán)衡算法全局與局部搜索能力,該因子更新計(jì)算如式(4)所示,另外,c1、c2為算法的兩個(gè)調(diào)節(jié)系數(shù),同樣為了調(diào)節(jié)算法的全局與局部搜索范圍,具體計(jì)算如式(5)所示,而r1與r2為兩個(gè)0,1之間的隨機(jī)數(shù)。
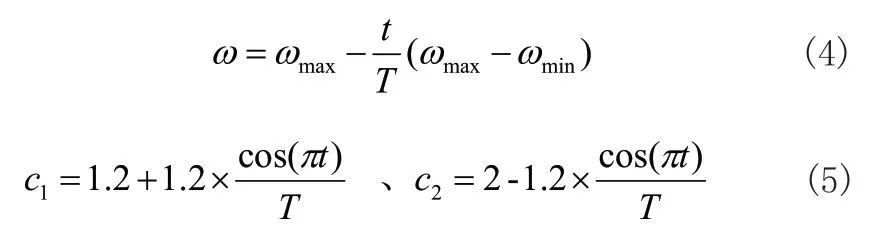
對于算法中個(gè)體移動方向與距離,參考了BAS算法的個(gè)體特性。對于BAS算法個(gè)體左右須位置Xir,Xil計(jì)算如式(6)所示:
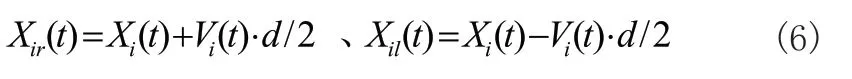
由此算法中個(gè)體移動距離與方向更新如式(7)所示:
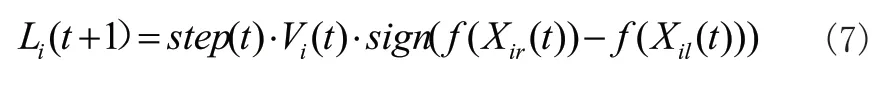
式中,步長step(t)按式(8)進(jìn)行更新。
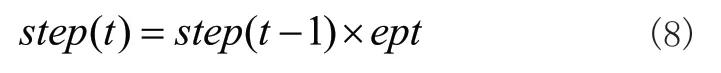
式中ept為變步長因子,從而未加入Levy飛行機(jī)制的算法個(gè)體更新計(jì)算如式(9)所示:
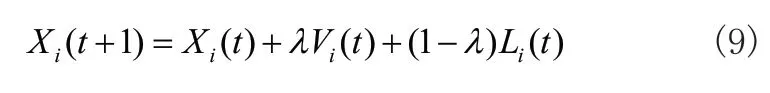
式中λ為步長比例因子,本文取0.4。由于Levy的長期短距離飛行、短期長距離飛行機(jī)制能夠有效提高算法個(gè)體的多樣性,從而提高算法的搜索范圍,進(jìn)而有效抑制易早熟現(xiàn)象的發(fā)生[8]。
對于Levy飛行機(jī)制所服從的Levy分布計(jì)算式如式(10)所示:
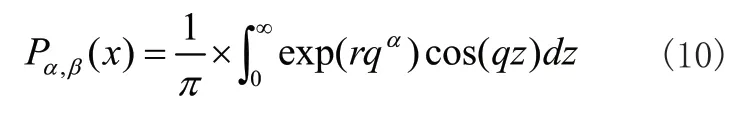
其中,α取值范圍為[0,2],主要用于控制Levy分布圖峰的銳度,r為控制分布圖跨度的參數(shù)取值應(yīng)大于0。對于α,當(dāng)其取值為非整數(shù)時(shí),難以利用Levy分布的概率密度函數(shù)對問題進(jìn)行分析,一般采用模擬方法來生成Levy分布的隨機(jī)步長,因而對于加入Levy飛行機(jī)制的BSO算法的位置更新式如式(11)所示:
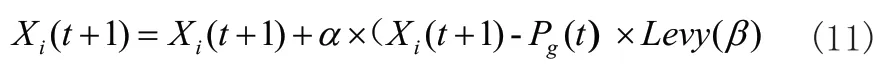
其中α為隨機(jī)步長,文中經(jīng)過多次實(shí)驗(yàn),取值為0.45,對于Levy(β)為符合式(12)約束的隨機(jī)搜索路徑。
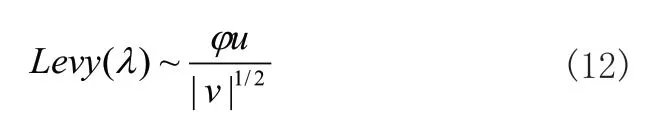
其中u,v服從標(biāo)準(zhǔn)的正態(tài)分布,對于φ計(jì)算如式(13)所示:
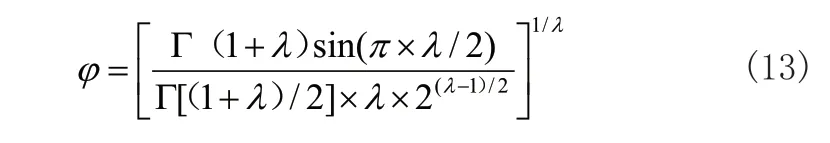
由上可得Levy-BSO算法流程圖如圖1所示。
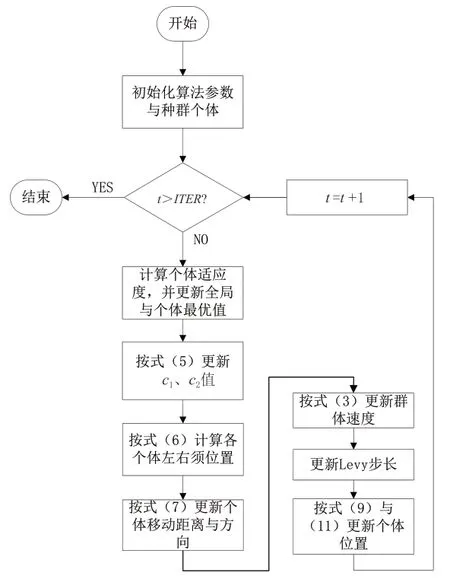
圖1 LBSO算法運(yùn)行流程
3 LBSO-PID控制器的設(shè)計(jì)
3.1 LBSO-PID控制原理
利用LBSO對PID控制器比例、積分以及微分參數(shù)進(jìn)行優(yōu)化整定,即通過實(shí)現(xiàn)對控制誤差的采集與計(jì)算來實(shí)現(xiàn)對上述三個(gè)參數(shù)進(jìn)行優(yōu)化調(diào)節(jié),進(jìn)而使系統(tǒng)綜合性能實(shí)現(xiàn)最優(yōu),對于LBSO-PID控制器的具體實(shí)現(xiàn)框圖如圖2所示。
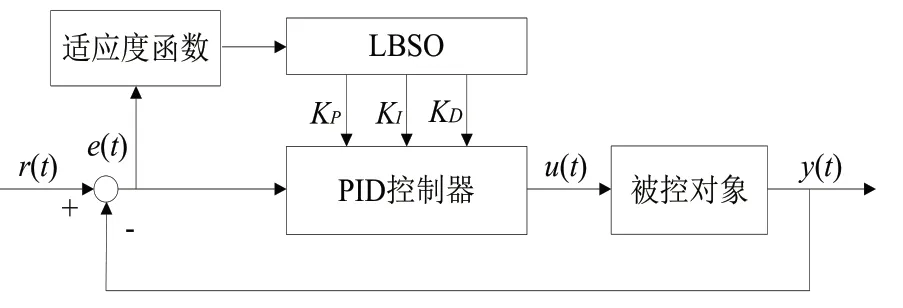
圖2 LBSO-PID控制框圖
3.2 適應(yīng)度函數(shù)
為了實(shí)現(xiàn)對被控對象的良好控制,還須選擇一個(gè)合適的適應(yīng)度函數(shù)。由于僅考慮輸出誤差,那么系統(tǒng)的響應(yīng)速度得不到保障,而若僅考慮響應(yīng)速度,那么系統(tǒng)的穩(wěn)定性會很低,因而本文選擇了一種基于時(shí)間誤差絕對值的適應(yīng)度函數(shù)ITAE,其具體計(jì)算方式如式(14)所示:
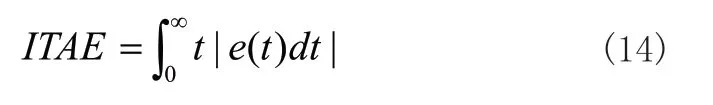
對式(14)進(jìn)行離散化處理可得到式(15):
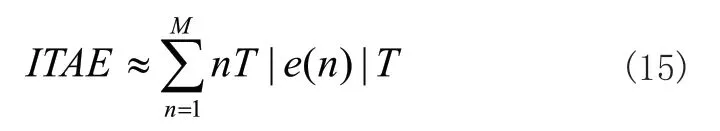
其中,n為采樣的次數(shù),M為總的采樣次數(shù),T是采樣周期。
4 控制效果驗(yàn)證
為了驗(yàn)證所提方法的有效性以及優(yōu)越性,本文分別利用所提方法以及基于PSO的PID參數(shù)自整定方法分別對如式(16)所示的一階延時(shí)系數(shù)以及二階系統(tǒng)進(jìn)行單位階躍響應(yīng)PID控制參數(shù)整定。對于PSO以及LBSO參數(shù)設(shè)置分別如下。設(shè)置PSO最大與最小慣性因子分別為0.9與0.2,兩個(gè)學(xué)習(xí)因子均為1.2。設(shè)置LBSO初始步長為20、須寬為6、變步長因子為0.995,最大與最小慣性因子分別為0.9與0.2,其它參數(shù)如前節(jié)所述。設(shè)置兩種算法迭代次數(shù)均為150次,種群數(shù)均為20。利用上述算法對PID參數(shù)進(jìn)行整定的結(jié)果分別如表1與圖3、圖4所示。
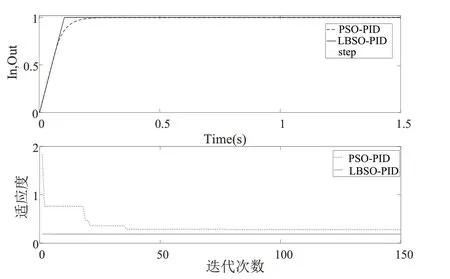
圖3 G1系統(tǒng)控制響應(yīng)結(jié)果
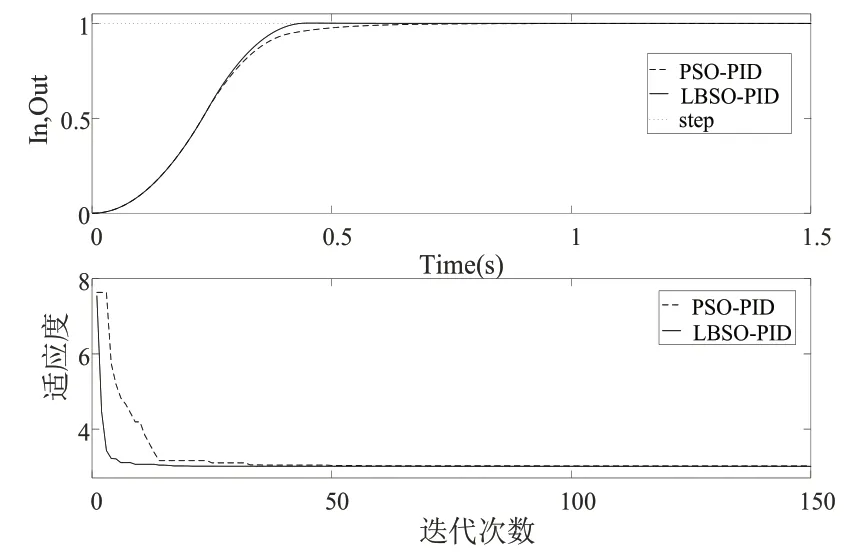
圖4 G2系統(tǒng)控制響應(yīng)結(jié)果
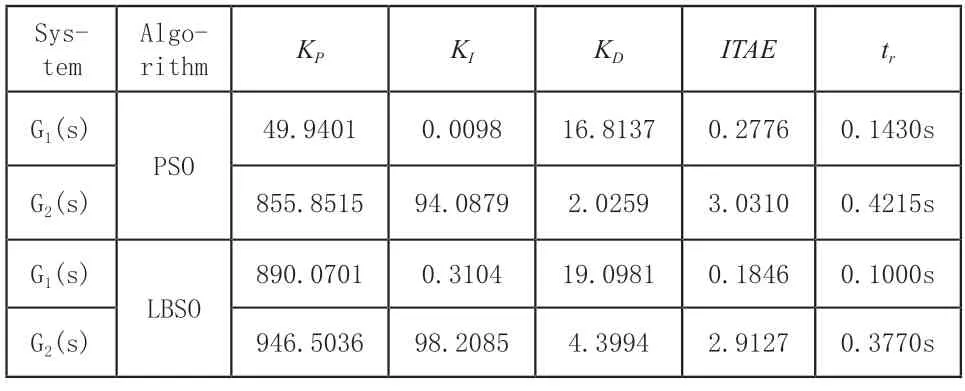
表1 控制計(jì)算結(jié)果表
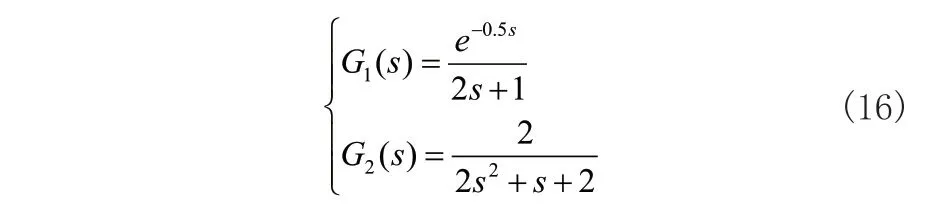
由表1給出的計(jì)算結(jié)果以及圖3與圖4可以看出,本文所提的LBSO-PID自整定方法在對G1系統(tǒng)的整定,在時(shí)間誤差絕對值上相對PSO-PID自整定方法相對減少了約33.5%,而在上升時(shí)間上相對減少了30%多,而對于G2系統(tǒng)的整定,在時(shí)間誤差絕對值上相對減少了近4%,在上升時(shí)間上相對減少了10.5%多。由此可以看出本文所提方法在控制精度上以及控制速度上相對PSO-PID自整定方法有著很大的優(yōu)勢。另外,由迭代結(jié)果可以看出,本文所提LBSOPID自整定方法在迭代速度上相對PSO-PID自整定方法也有著非常明顯的優(yōu)勢,由此進(jìn)一步驗(yàn)證了LBSO算法在PID參數(shù)整定計(jì)算中的優(yōu)勢。
為了進(jìn)一步驗(yàn)證所提方法在工業(yè)控制中的有效性與普遍適用性,給出所提方法對文獻(xiàn)[9]所給出的空壓機(jī)控制系統(tǒng)PID參數(shù)整定結(jié)果如圖6與表2所示。空壓機(jī)控制系統(tǒng)傳遞函數(shù)如式(17)所示,給出對于該系統(tǒng)的階躍響應(yīng)的結(jié)果。
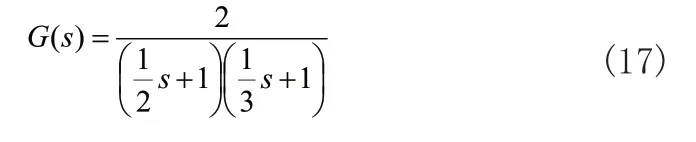
由圖5以及表2給出的計(jì)算結(jié)果再次驗(yàn)證了,本文所提LBSO-PID對空壓機(jī)系統(tǒng)的控制中,無論在響應(yīng)速度還是控制精度上均優(yōu)于PSO-PID方法。另外,由文獻(xiàn)[9]所給出的方法的計(jì)算結(jié)果可以看出,該方法對于空壓機(jī)控制系統(tǒng)階躍響應(yīng)的控制過程中,系統(tǒng)達(dá)到穩(wěn)定所需時(shí)間為1s,而本文所提方法僅需0.1211s。
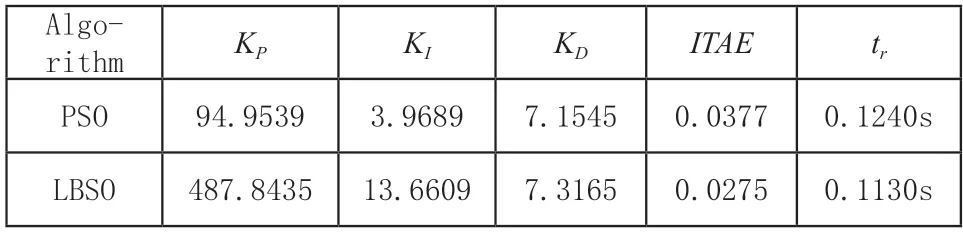
表2 空壓機(jī)控制系統(tǒng)參數(shù)整定結(jié)果
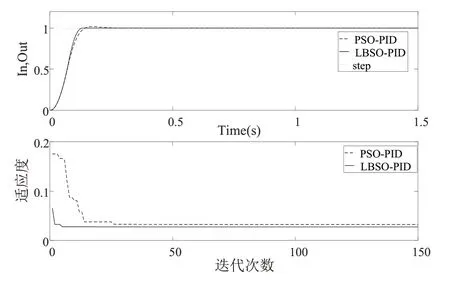
圖5 空壓機(jī)控制系統(tǒng)響應(yīng)結(jié)果
5 結(jié)語
為了提高PID在工業(yè)控制中的效果,本文提出了一種基于LBSO算法的PID參數(shù)自整定方法。針對原始BAS算法存在的求解精度低、迭代速度慢以及易早熟的問題,本文引入PSO算法的種群特性以及Levy隨機(jī)步長特性,有效提高了算法的求解精度以及迭代速度。將LBSO算法應(yīng)用于PID參數(shù)自整定中,利用一階延時(shí)系統(tǒng)、二階系統(tǒng)以及空壓機(jī)工業(yè)控制實(shí)例對其控制有效性以及優(yōu)越性進(jìn)行了驗(yàn)證。

