基于CEEMDAN和SVM的混凝土破壞狀態聲發射信號識別

宿 輝，欒亞偉，胡寶文，白延杰

(1.河北工程大學水利水電學院，河北 邯鄲 056038； 2.河北省智慧水利重點實驗室，河北 邯鄲 056038)

隨著我國水利建設不斷發展，越來越多的混凝土材料被應用于水利工程中。混凝土狀態直接決定了水利工程的安全性。因此，混凝土材料早期破壞狀態的識別診斷對水利工程的安全運行至關重要[1-2]。聲發射技術是目前一種較成熟的無損監測技術，近年來被逐漸用于探尋混凝土破壞狀態監測方面的問題[3]。通常對包含混凝土內部損傷信息的聲發射信號進行濾波處理，可以精準地提取混凝土破壞過程中的相關參數，進而獲得混凝土的損傷信息[4]。例如：袁明等[5]采用快速傅里葉譜變換和小波包分解方法，分析了混凝土裂縫擴展過程中聲發射信號，發現混凝土宏觀裂紋波形相對于微觀裂紋波形更為復雜；趙奎等[6]應用集合經驗模態分解(EEMD)及單通道盲源分離(SCBSS)方法對巖石聲發射信號進行了濾波處理，發現該方法可以有效保護濾波后聲發射信號的頻域信息，但該算法添加的高斯白噪聲會影響聲發射信號的分解。由于傅里葉變換和小波分解法[7]并不能對非平穩的聲發射信號進行完全的去噪處理，Torres等[8]提出了自適應噪聲完備集合經驗模態分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)方法，其通過對各階殘余量添加自適應白噪聲，可有效獲取一定數量不同頻率的自適應特征模態(IMF)分量，且重構誤差趨于0，因此，其對非線性時間序列的分解效果更好。

與傳統的神經網絡[9]和隨機森林[10]等機器學習方法相比，支持向量機(support vector machine，SVM)方法[11-12]的優勢在于：適用于小數量樣本學習，簡化了通常的分類問題，具有很好的魯棒性。因此，SVM可以有效解決復雜非線性問題中的預測難題。例如：吳鑫等[13]將聲發射信號的能量、幅值等特征參數輸入神經網絡模型中，減小了巖石聲發射事件源定位誤差；吳賢國等[14]把混凝土材料用量作為參數輸入到RF-SVM模型中做回歸預測，得到的預測結果精度接近實測值。

本文將CEEMDAN方法與SVM方法耦合使用，提出了一種混凝土破壞狀態聲發射信號耦合識別模型，探究其對混凝土破壞階段特征提取的可行性和預測混凝土破壞階段的準確性。

1 試驗方案

1.1 試驗材料與方法

為了保證試驗的準確性，本次試驗混凝土試塊規格為100 mm×100 mm×200 mm，水泥為太行山牌P·O 42.5普通硅酸鹽水泥，粗骨料為5～15 mm連續級配的碎石，細骨料為當地河砂篩選出，粉煤灰選自當地電廠生產的Ⅱ級粉煤灰，減水劑采用聚羧酸高性能減水劑。

在YH-60B型混凝土標準養護箱養護，養護濕度在95%以上，溫度設定為(20±1)℃，養護齡期分別為1 d、3 d、7 d和28 d，強度等級為C30，1 m3混凝土配合比參數包括：水膠比0.42，水198 kg，水泥424 kg，粉煤灰47 kg，碎石1 186 kg，砂582 kg，減水劑1.2 kg。試件共計4組，每組3個試件作為平行試驗，共計12個試件，分別對其進行聲發射單軸壓縮試驗，計算各組試件的平均值，當一個試件抗壓強度與平均值超過15%時，重新做試驗。最后從中選取養護齡期為28 d的工況進行研究。

1.2 試驗儀器

加載系統為TAW-2000微機伺服三軸試驗機，此次加載方式為位移控，加載速率為0.1 mm/min。聲發射系統采用PCI-2型多通道高速采集聲發射試驗儀，傳感器采用R6-a型，頻率帶寬范圍為10～110 kHz,聲發射門檻值38 dB，峰值定義時間50 μs，采樣率設定1 MSPS，撞擊定義時間100 μs，閉鎖時間300 μs。

2 聲發射信號分析

2.1 混凝土損傷信號預處理

在聲發射監測過程中將得到能量、幅值等特征參數，其中前者可以很好地反映混凝土在破壞過程中的狀態[15]。圖1為混凝土在單軸壓縮過程中聲發射信號能量-時間和荷載-時間變化曲線。值得注意的是聲發射能量可以有效評估混凝土裂紋的變化情況，即裂縫越劇烈，能量越大。

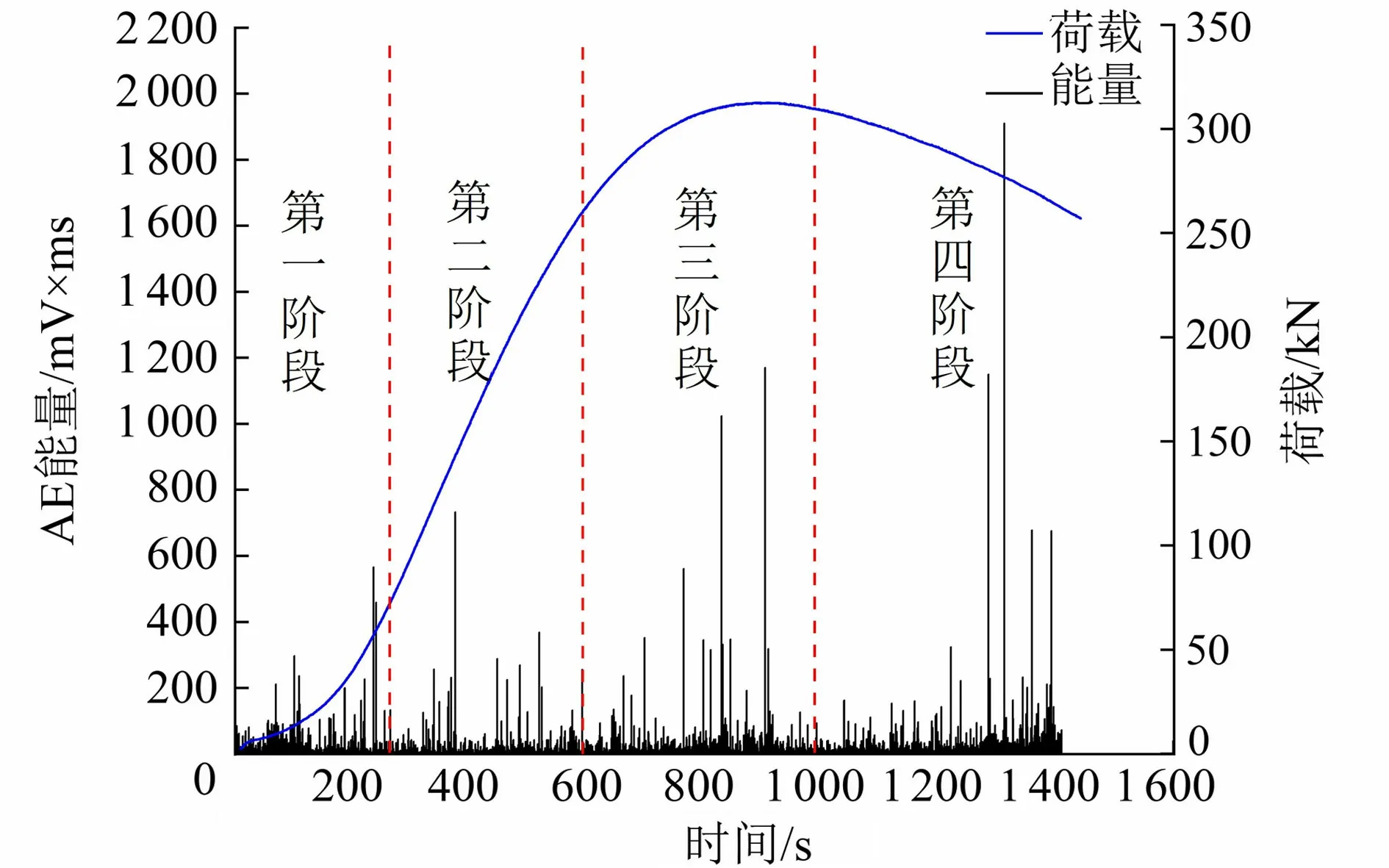
圖1 能量-荷載-時間曲線

圖1表明，在混凝土破壞過程中，混凝土內部的能量在大多數時間處于均衡釋放狀態，整體呈現“聚集-釋放-再聚集-再釋放”的演進過程，但在230 s、370 s、915 s、1310 s附近能量曲線存在局部峰值現象，這歸因于混凝土將前一時段內聚集的能量集中釋放，其突變點意味著混凝土裂紋發展到最劇烈時刻；在加載初期，混凝土中原始存在的微孔隙在荷載的作用下逐漸閉合，產生一定的聲發射信號。隨著荷載的增大，混凝土中逐漸有裂紋萌生，荷載繼續增大，原始的裂紋進一步發展至試件表面，進入最后一階段，荷載減小，混凝土材料損傷達到極限狀態，根據荷載-時間曲線結合峰值出現的位置和裂紋在破壞過程中的變化過程，可以將整個混凝土破壞過程分為微孔隙閉合、裂紋萌生、裂紋發展、裂紋貫通4個階段，其相關參數見表1。

表1 不同破壞階段的數據集

圖2為混凝土破壞過程中聲發射幅度分布規律4個階段中選取的典型信號波形圖。通過對不同階段去噪分解前聲發射信號波形的對比發現，隨著裂紋的不斷發展，聲發射信號的幅值逐漸變大、波形復雜程度增大，且在0.01V處存在雙波、三波以及難以分辨波形個數的多波。

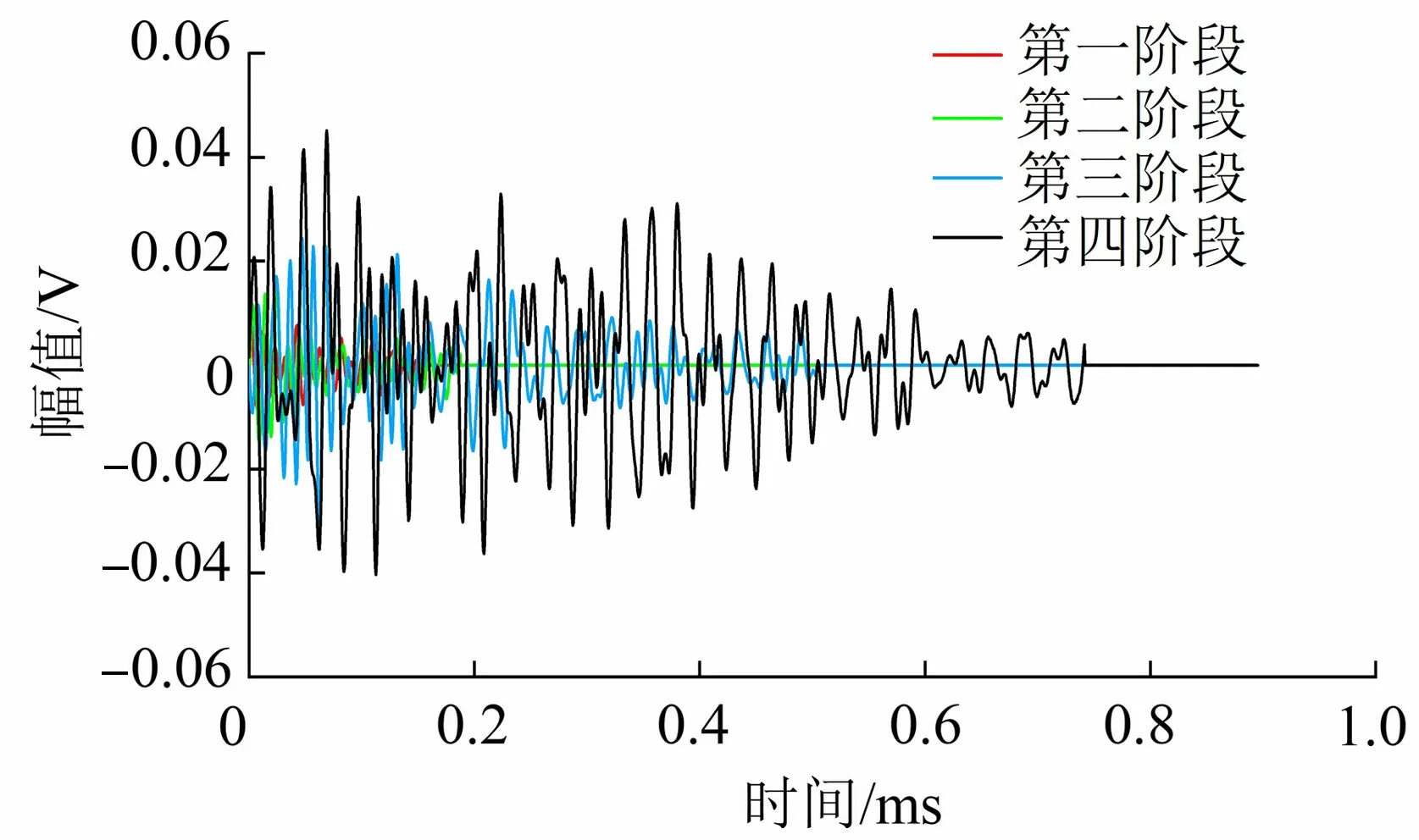
圖2 不同破壞階段典型波形

綜合分析表1和圖2可知，4個階段的持續時間依次增加，同時考慮數據的處理量以及SVM方法適用于小數量樣本學習，在借鑒王巖等[9]處理聲發射信號選取樣本的研究成果的基礎上，本文確定在第一階段隨機選取50個樣本，第二、三、四階段依次隨機選取55個、60個和65個樣本。

2.2 基于CEEMDAN的聲發射信號分析

基于MATLAB平臺，對混凝土不同破壞階段的聲發射信號進行CEEMDAN分解，各個聲發射信號均可以分解為10～12個IMF分量和一個殘差。

圖3為第一階段中一個原始信號，使用CEEMDAN法對原始信號進行分解，利用分解出的每個IMF分量與原聲發射信號的相關系數，可以確定每個IMF分量包含原聲發射信號頻域信息的程度。IMF1～IMF11分量與原聲發射信號的相關系數分別為0.539 4、0.602 1、0.883 7、0.680 1、0.432 4、0.220 9、0.019 9、0.005 3、0.001 5、0.023 3、0.028 4。如果求出的一階IMF與原信號的相關系數較之前幾階明顯小很多，可判定這一階是假的，應該去掉，計算亦隨之停止。從IMF7開始相關程度較之前急劇下降，基本為0，因此IMF1～IMF6包含了原聲發射信號中主要頻域信息。圖4和圖5分別為第一階段原始信號的CEEMDAN的IMF1～IMF6分量及其信號頻譜圖。

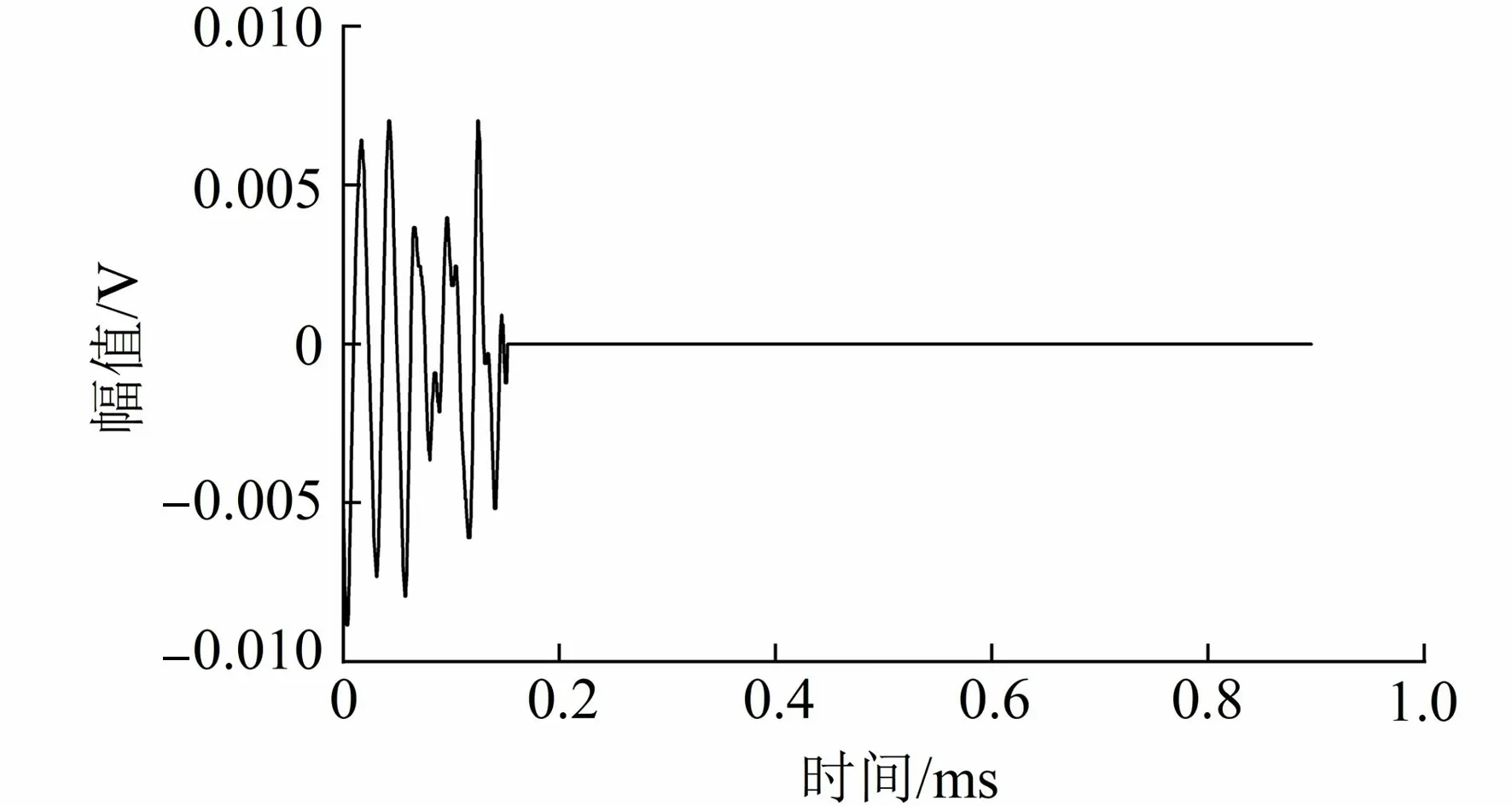
圖3 第一階段原始信號波形

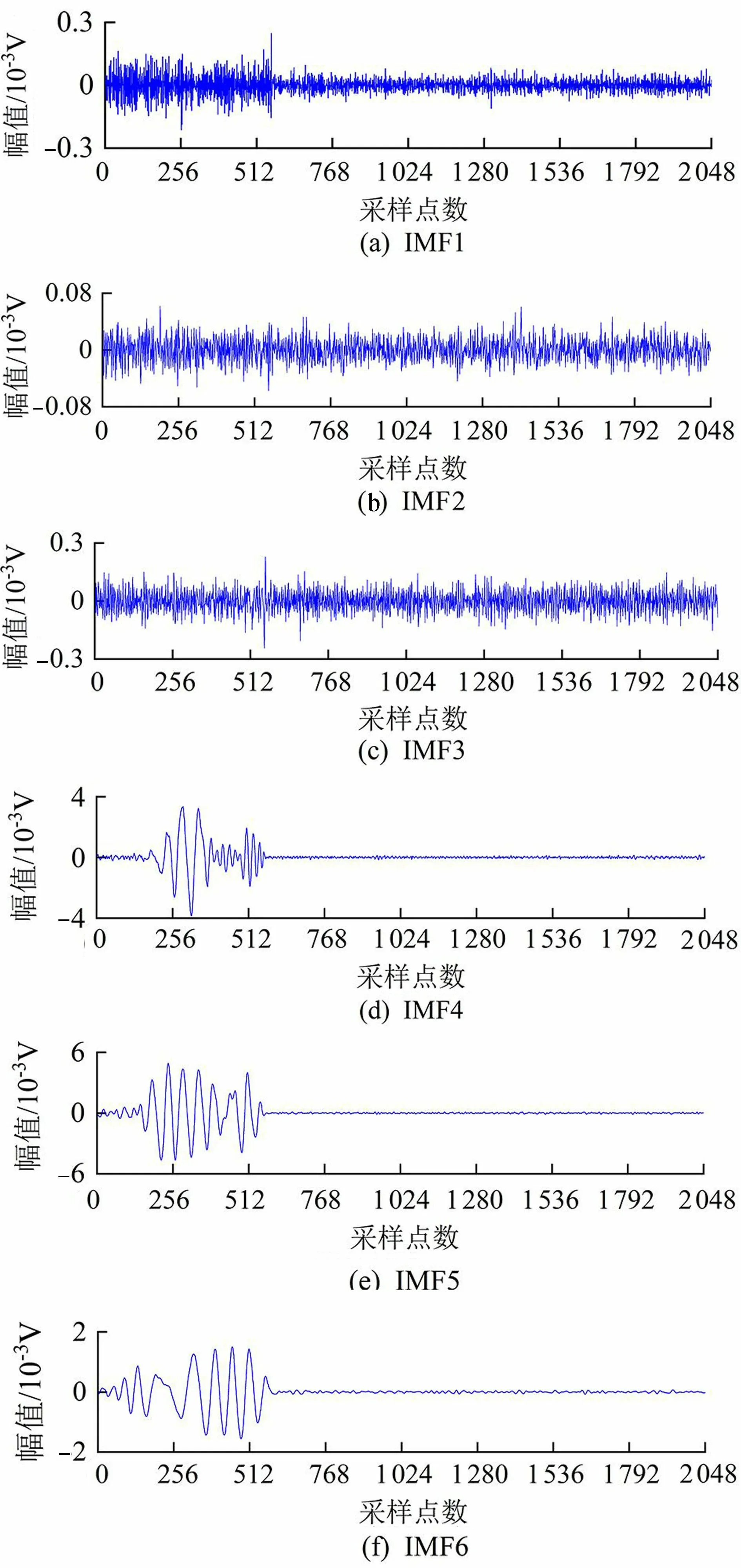
圖4 第一階段原始信號的CEEMDAN分解IMF分量

圖5 第一階段原始信號的CEEMDAN分解IMF分量信號頻譜

2.3 混凝土破壞聲發射信號特征提取結果

利用CEEMDAN分解得到的IMF1～IMF6分量特征參數能量系數Pe和波形系數Cs可以較好地揭示不同破壞階段特征，其計算公式為

(1)

(2)

式中：χij為第j個IMF分量的第i個數據值；N為信號總數據數；M為IMF分量總數；|χi|表示第i個數據點的絕對值。

值得指出的是能量系數是每個IMF分量占全部IMF分量能量的比值，在不同階段，其值差異顯著；波形系數是波形有效值與波形平均幅值的比值，不同階段的聲發射波形系數也存在差異。混凝土破壞聲發射信號特征參數值如表2和表3所示。

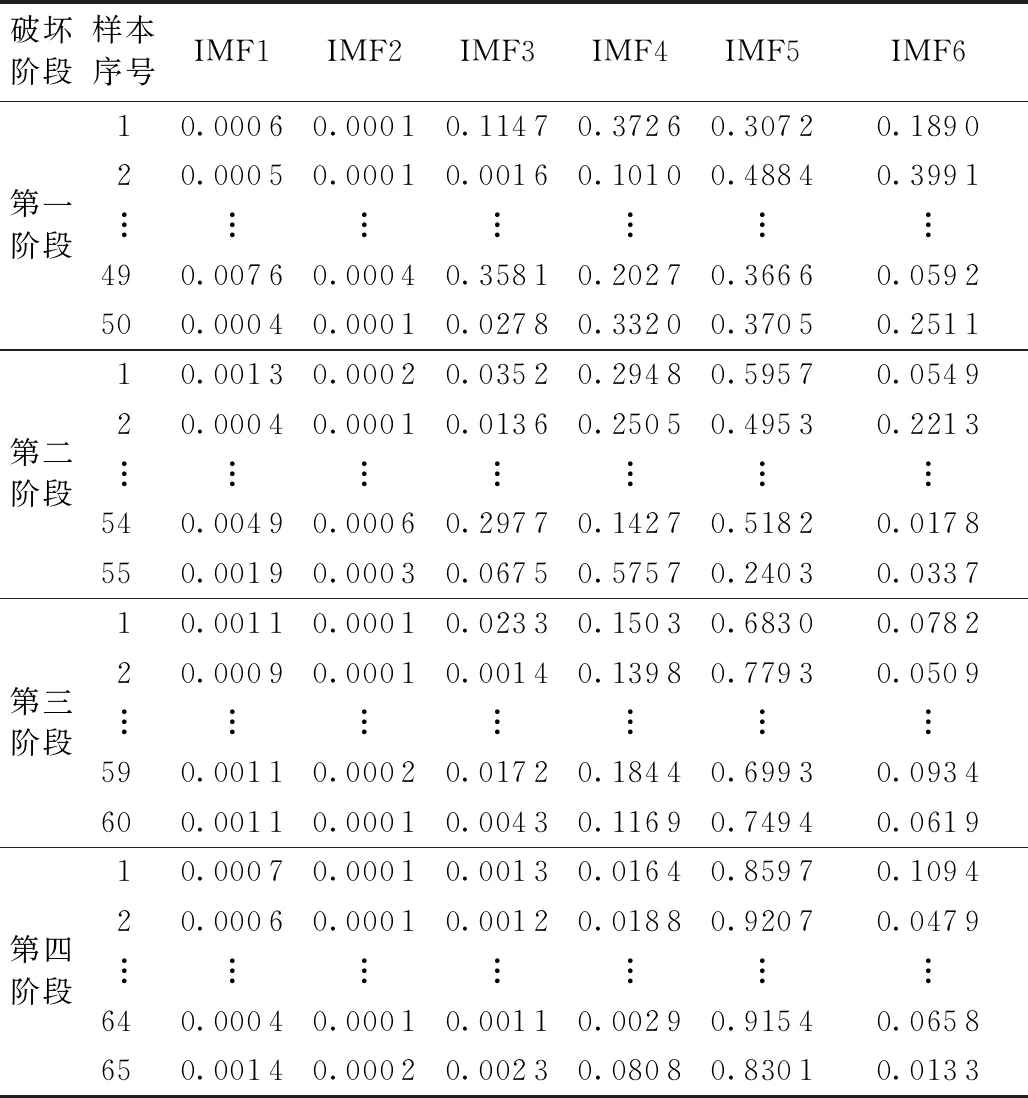
表2 SVM輸入特征能量系數

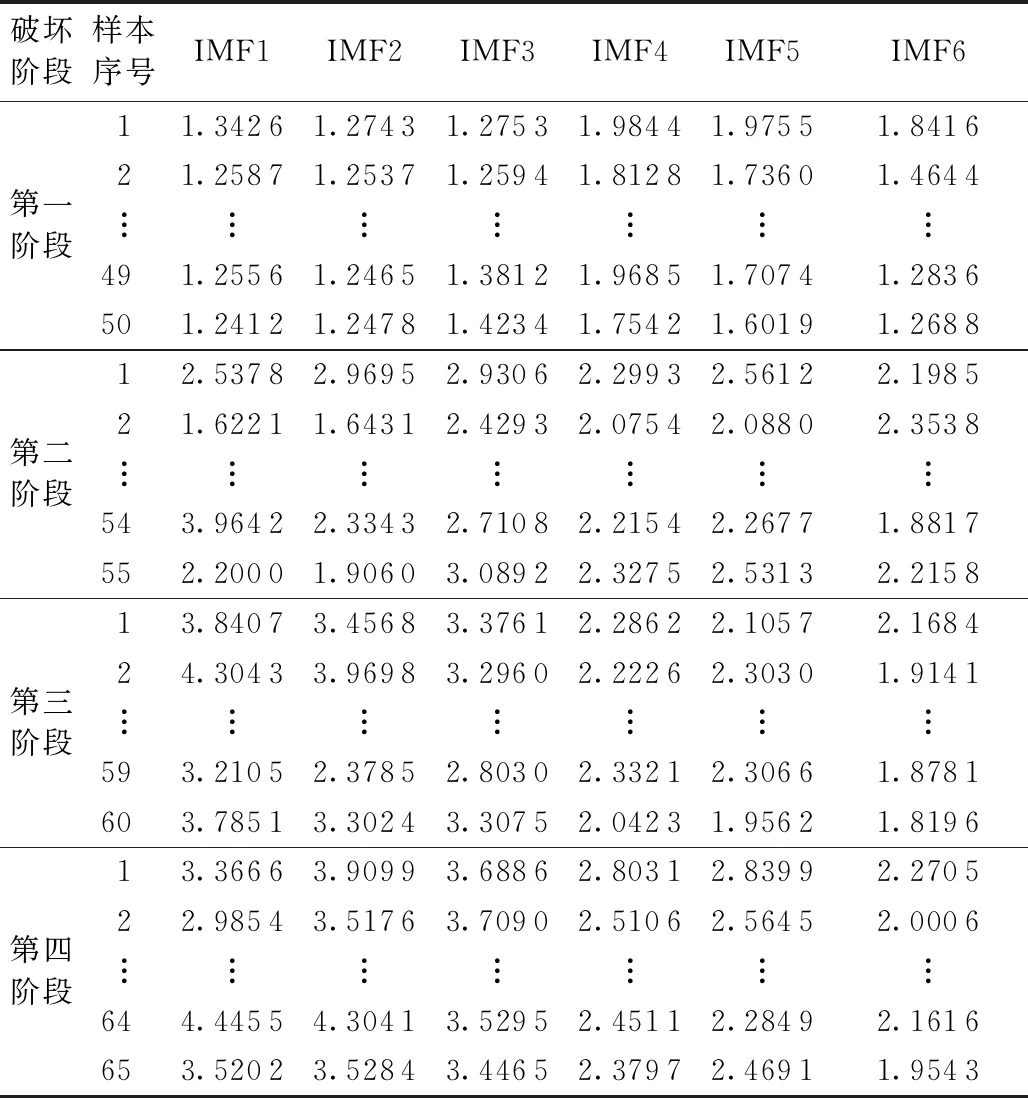
表3 SVM輸入特征波形系數

2.4 基于SVM的破壞狀態監測

2.4.1數據預處理

數據量綱不統一以及數據偏態分布均會降低SVM的求解速度和模型精度。因此，利用Python軟件中的StandardScaler對混凝土破壞聲發射信號原始數據進行歸一化和標準化處理，并將其輸入到SVM中，其計算公式為

(3)

式中：X為原始數據；μ為均值；σ為標準差。

2.4.2網格搜索和交叉驗證的參數優化

由于混凝土破壞聲發射數據具有高度非線性特征，在SVM訓練測試過程中，核函數選擇徑向基核(RBF)，并利用網格搜索法尋找出最優參數懲罰因子C和g。此外，考慮到訓練數據對參數的影響較大，且前一階段的最優參數將會隨之改變。因此，采用K-CV交叉驗證與網格搜索相結合的方式對每組(C，g)參數進行優選，即將訓練數據分為4組，其中3組作為訓練集，剩余1組作為預測集，最終優選得到4個模型，并將其分類準確率的平均值視為交叉驗證的評估指標。

圖6為能量系數和波形系數尋優三維等高線圖。SVM方法利用少量樣本就可以完成訓練學習，為了降低預測樣本數量不足易于造成的結果偶然性，故本文選擇每個階段的前60%作為訓練樣本，其余作為預測樣本，且把各信號分量IMF1～MF6的能量系數和波形系數作為SVM的輸入特征參數。SVM的輸出分為4類，分別為第一階段、第二階段、第三階段和第四階段。

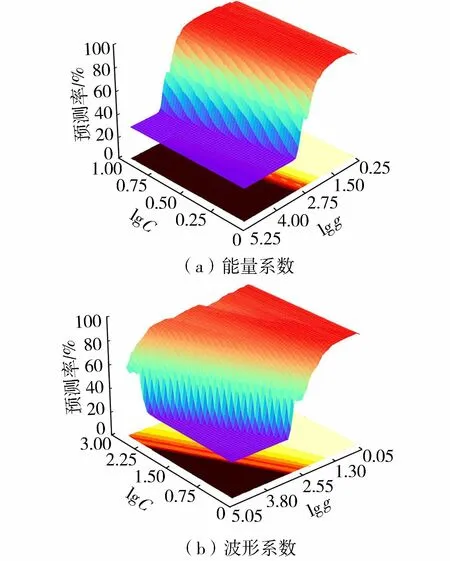
圖6 能量系數和波形系數尋優三維等高線

表4為混凝土破壞狀態預測結果(能量系數和波形系數分類結果)。由表4可知，將能量系數作為特征參數時，經過網格搜索和交叉驗證最終確定參數C的取值為8.3，參數g的取值為0.09，其準確率高達92.39%；將波形系數作為特征參數時，經過網格搜索和交叉驗證最終確定參數C的取值為1.02，參數g的取值為1.88，其準確率高達91.30%。

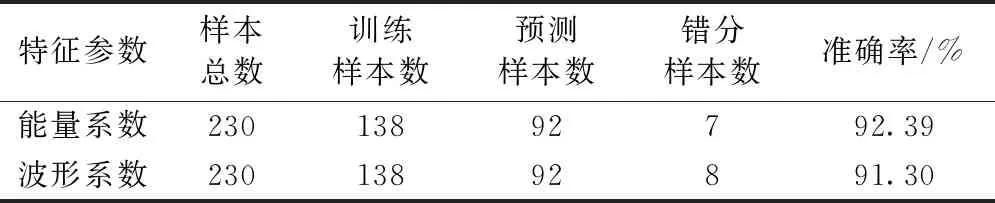
表4 能量系數和波形系數分類結果

3 結 論

a.基于CEEMDAN和SVM方法對混凝土破壞狀態識別是可行的，且利用IMF分量和原信號的相關性可有效剔除虛假分量。

b.利用網格尋優和交叉驗證方法優化SVM參數，可以提高診斷精度。

c.有效IMF分量的能量系數和波形系數作為特征參數時，其預測率分別為92.39%和91.30%，兩者均可以較優地揭示混凝土破壞的損傷特征。

d.提出的CEEMDAN與SVM耦合方法可有效進行混凝土破壞狀態的識別，研究成果可為評估混凝土結構安全狀態提供可靠的理論依據。