基于模糊綜合評價及TOPSIS模型的武威市水資源承載力評價及預測

李 龍，蔣天樂，李 磊，馬亞麗，孫棟元，黃 博，趙振宇

(甘肅農業大學水利水電工程學院，甘肅 蘭州 730070)

水資源是人類生存和發展的基礎，科學的管理模式對于水資源可持續發展利用具有重要的意義[1]。隨著社會經濟的飛速發展，科學技術的突飛猛進，人類對水資源的需求量也在不斷地增加，這使得水資源問題日益凸顯。特別是城鎮人口過快增長、工業用水量急劇上升，進而對水資源保護和利用提出了新的要求[2]。水資源的分配作為影響國計民生的大問題，受到越來越多的重視。利用數學知識研究分配方案，實現宏觀調控，成了解決水資源分配的重要方法之一。2011年，中央一號文件《中共中央國務院關于加快水利改革發展的決定》提出要實行最嚴格水資源管理制度[3]。在十九大報告中習近平總書記明確指出“必須樹立和踐行綠水青山就是金山銀山的理念”。2020年5月，全國政府工作報告中指出要加強污水、垃圾處置設施建設，實施重要生態系統保護和修復重大工程，促進生態文明建設[4]。

目前，西北干旱地區的水資源承載力供需矛盾日益加劇，重點區域的水資源承載力評價研究亟需開展[5]。武威是絲綢之路經濟帶的重要節點城市，2020年我國全面建成小康社會后，如何在水資源匱乏的情況下，建成可持續發展的綠色武威具有重要意義。張桂林[6]認為西北地區水資源承載力處于瀕臨超載和水資源利用輕度不協調狀態。許程程[7]研究表明甘肅省水資源承載力整體呈上升發展趨勢。張亮[8]通過層次分析法對區域水資源可利用程度進行評價。吳明艷等[9]認為西北五省區水資源承載力水平呈緩慢提升態勢，由水資源短缺狀態轉變為水資源合理狀態。柳盼盼[10]在對甘肅省水資源承載力評價中認為甘肅省水資源承載力越來越小，水資源總量近些年來一直呈現下降趨勢。劉曉敏[11]通過運用熵權法對武威市2005—2017年的水資源脆弱性進行了評價。任曉燕等[12]通過主成分分析法對武威市水資源承載能力進行評價。已有研究采用的方法相對單一，文章中將模糊綜合分析法與TOPSIS模型創新性地結合，構建武威市水資源承載力評價指標體系，并對武威市水資源承載力進行評價與驗證，2種綜合評價方法取長補短，增加了文章的可信度，采用GM(1，1)灰色預測模型對武威市未來水資源的發展趨勢進行預測分析。研究成果為解決武威市所面臨的水資源匱乏和水資源安全問題提供重要的參考依據。

1 數據來源

1.1 研究區概況

武威市地處河西走廊東段。屬溫帶大陸性氣候，年平均蒸發量2163.6mm，年均降水量為212.1mm，降雨集中在6—9月，八月最多，四季分布不均[13]。全市多年平均水資源總量為14.934億m3，多年平均徑流量為0.31億m3，地下水主要靠大氣降水和冰川融水。近年來，受到全球氣候變化以及人類活動的影響，武威市內大部分地方氣候干燥，降水稀少，降水量自東北向西南隨海拔增加而增加。特殊的地理位置更加凸顯了水土保持在全市經濟社會發展的重要位置[14]。

1.2 數據來源

本文對甘肅省武威市水資源承載力的各類影響因素進行收集，主要數據來源于2010—2020年的《甘肅省水資源公報》。

2 研究方法

關于水資源承載力的研究有熵權法、模糊綜合評價法、優劣解距離法(TOPSIS)和灰色預測模型。影響水資源承載力的因素有生態、資源、經濟等多個方面，同時還必須充分考慮到評價指標的綜合性和可信性。因此，本文通過使用熵權法對武威市水資源進行權重的確立，并結合模糊綜合評價法和TOPSIS模型計算綜合評價值，并對未來趨勢進行預測，利用殘差檢驗擬合精度。

2.1 構建評價指標體系

武威市水資源評價指標體系建立要以科學性、實用性、區域性和全面性為原則，構建由多個子系統構成的復雜系統，在借鑒國內外學者對水資源承載力的研究成果，同時結合武威市各指標數據的可獲得性[15]，構建由水資源、社會、經濟、生態環境4個準則層，22個指標組成綜合評價指標體系，如圖1所示。并將評價指標分為可承載(V1)、超載(V2)、嚴重超載(V3)3個等級，見表1。

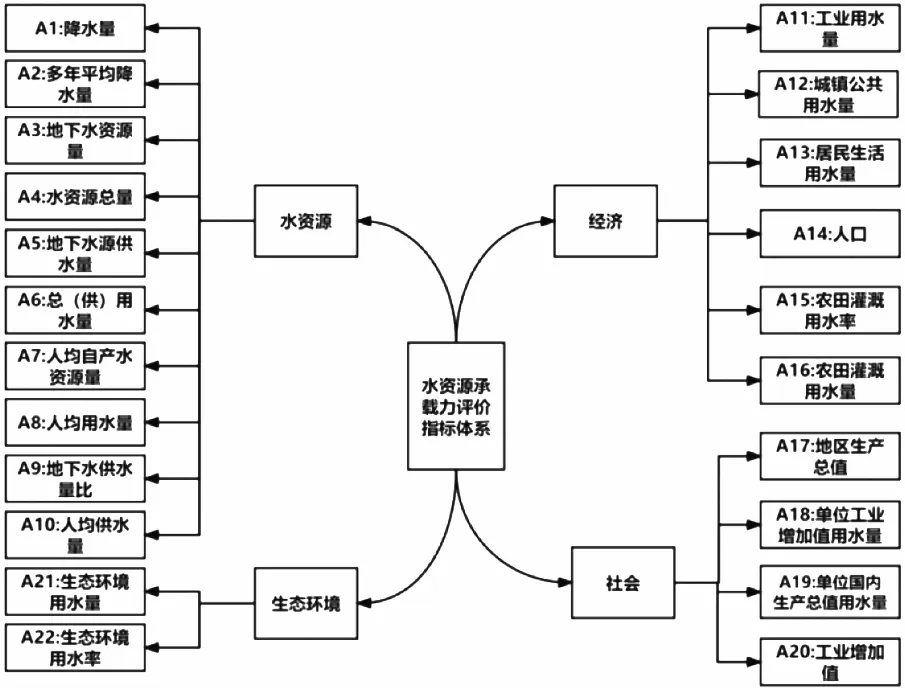
圖1 武威市水資源評價指標體系

2.2 數據標準化

首先對武威市水資源承載力的各項評價指標進行標準化處理，目的是消除指標不同單位帶來的結果誤差。在判斷矩陣X中，假定有評價對象m個，每個評價對象對應n個指標。

X=(xij)mn，i=1，2，…，m;j=1，2，…，n

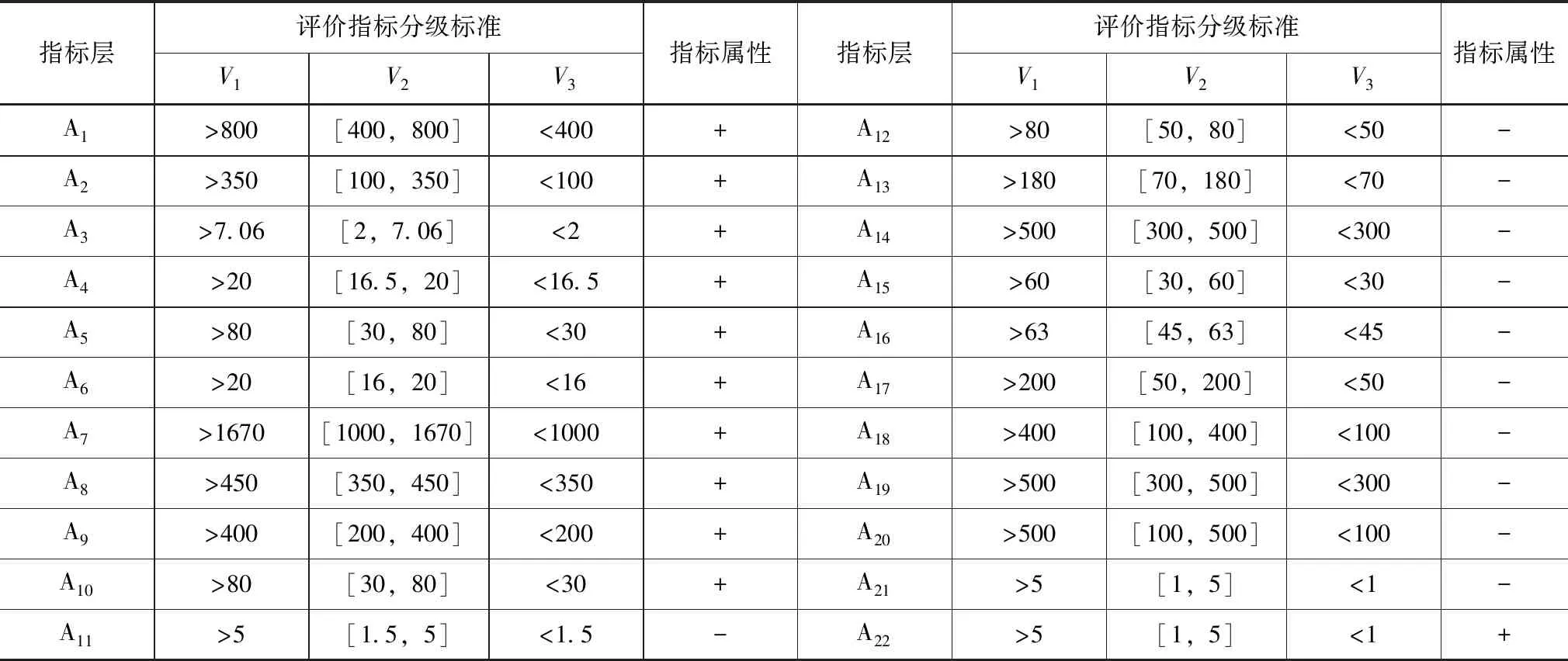
表1 武威市水資源評價指標體系分級標準

對原始數據進行標準化處理后得到標準化矩陣Y，Y對于偏大型指標和偏小型指標有以下計算方法：

(1)當指標值越大越好時

(1)

(2)當指標值越小越好時

(2)

2.3 熵權法

熵權法可以利用樣本中的數據在各評價指標中來確定權重，是一種常見的能消除主觀因素的一種客觀賦權法[16]，可以更好地對結果進行解釋。熵值評價指標值由變異程度決定，利用信息之間的差異性，對各項水資源指標進行標準化處理，避免無關因素影響實驗結果。線性加權法運算原理的運用，則是通過疊加對承載力不同影響程度的各評價指標，計算出一個綜合值進行水資源承載力的評價。綜合值越大，水資源承載力越強，綜合值越小，水資源承載力越弱[17]。

(1)求評價指標的信息熵E：

(3)

(4)

其中Pij=0時，則定義limpijlnpij=0

(2)確定各個指標的權重

各個指標的權重集Wi為：

(5)

2.4 模糊綜合評價法

模糊綜合評價法可以把具有一定性質的因素進行量化評價，是根據模糊數學的隸屬度原則來定義的，受多重因素的影響和制約，統計這些影響因子需運用模糊數學的方法進行整體性評價[18]。這種方法在處理各種難以用精確數學方法描述的復雜系統問題方面表現出獨特的優越性[19]。

(1)確定評價因素和評價等級

構建評價因素集合：設X={x1，x2，…，xn}，x為評價對象的n種評價指標，其中n表示評價指標的數量。構建評價等級集合：設V={v1，v2，…，vn}，為評價等級的m種評價等級，其中m表示評價指標的數量，vj代表第j個評價對象的評價結果，本文將評價結果分為3個等級，分別為嚴重超載，超載，臨界承載。

(2)建立隸屬度矩陣

在得到指標所占權重后，對各個評價指標的隸屬度進行量化，即確定各個評價指標對評價指標集各等級的隸屬度[17]。以rij表示，然后得到隸屬度矩陣R。隸屬函數表達式如下：

(6)

(7)

(8)

(9)

(10)

式中，k1—v1評價等級的邊界值；k2—v2的中間值，即k2=(k1+k2)×0.5；k3—v3的邊界值。

公式(6)、(7)、(8)是針對偏大型指標而言的，對于偏小型指標的隸屬度計算只需將上述公式中“≥”改為“≤”“<”改為“>”即可。

(3)合成綜合評價向量B

B={b1，b2，b3，…，bj}=W·R

(11)

其中，W={w1，w2，w3，…，wj}，表示每個指標的權重系數。

(4)為能更好地反映區域時間維度上水資源承載力的變化，v1，v2，v3賦值，分別表示水資源承載力狀況為可承載、超載、嚴重超載。即v=0.9，v=0.5，v=0.1。根據公式得出綜合評價值A：

(12)

式中，k—各等級評價指標對武威市水資源承載力的影響程度的大小，在本次研究中k=1。

2.5 TOPSIS法

TOPSIS法又稱優劣解距離法，它依據評價方案與理想解的歐氏距離來進行評價方案的優劣排序[20]。其基本原理是通過分析樣本對象的優劣狀態，建立樣本對象最優(最劣)方案即正(負)理想點，并確定樣本對象與正(負)理想點的距離，進而求得樣本對象與理想點的貼近程度[21]。該方法能充分利用原始數據信息反映各方案之間的差距和實際情況，真實、直觀、可靠，且對樣本資料沒有特殊要求[22]。具體計算步驟如下：

步驟1原始數據同趨勢化區分指標體系中的指標類別(高優或低優)，并對不同類型的指標標準按照不同的公式進行正向化處理。構建n行m列的矩陣Xij，矩陣中X表示第i個對象的第j個指標的值。

步驟2構建標準化矩陣

(13)

步驟3 計算各評價指標與最優及最劣向量之間的差距與最優方案的加權歐氏距離為：

(14)

與最劣方案的加權歐氏距離為：

(15)

式中，wj—第j個屬性的權重(重要程度)。

步驟4測度評價對象與最優方案的接近程度

(16)

在計算結果中，若Ci值越大，則表明評價對象靠近正理想距離。根據Ci大小進行排序，給出評價的結果。

2.6 灰色預測(1，1)模型

灰色預測的主要特點是模型不通過原始數據序列進行計算，而是通過模型的計算生成的數據序列[23]。其核心體系是灰色模型(Grey Model，簡稱GM)，即對原始數據做累加生成(或其他方法生成)得到近似的指數規律，再進行建模的方法[24]。

將數據排列形成數組x0=[x0(1),x0(2),…x0(n)]，將x0作為數據列建立GM(1，1)模型如下：

x0(k)+az(1)(k)=b

(17)

其中a、b的值通過回歸分析的方法求解，得到白化模型為：

dx(1)(t)/dt=ax(1)(t)=b

(18)

x(1)(t)=[x0(1)-b/a]e-a(t-1)+b/a

(19)

得到預測值：

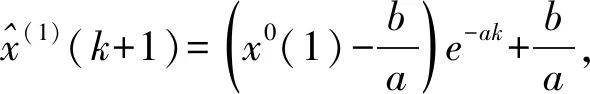
(20)

然后得到相應的預測值：

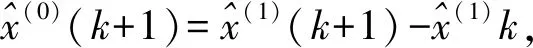
(21)

2.7 檢測模型預測值

通過對級比值、殘差、相對誤差、級比偏差進行檢驗，來驗證預測結果的合理性。

(1)相對誤差值越小，說明計算結果越精確。該值小于20%時達到要求，小于10%說明達到較高要求。

(2)級比偏差值越小結果越精確，小于0.2時達到要求，小于0.1說明達到較高要求。若所有的級比值都位于區間(e(-2/(n+1))，e(2/n+1))內，說明數據適合模型構建。

3 結果與討論

3.1 基于熵權法的權重計算

基于武威市2010—2020年的22個主要因素作為評價要素，通過對原始數據的分析，在社會層面，武威市工業用水量在2016年達到最大1.0548億m3，隨著工業的不斷發展，單位工業增加值用水量降低了64.2%，致使工業用水量降低到0.2145億m3。居民生活用水量由2010年0.478億m3增加到0.5846億m3。在經濟層面，地區生產總值較2010年提升了2.3倍，表明了武威市的經濟發展迅速。在水資源層面，武威市降水量幾乎沒有增加或降低，隨著科技的發展和社會的不斷進步，人均自產水量提高了18.96%。隨著人們生活水平在不斷提高，總用水量也隨之提高。在生態環境層面，生態環境用水率提高了4.84%。

熵權法的權重計算結果見表2，其中由于武威市工業發展趨勢較好，工業用水量增加，單位工業增加值用水量指標占比最大為0.088；由于武威市的地理位置和氣候，導致生態環境較為脆弱，生態用水量較少，生態環境用水量指標占比最小為0.022；水資源承載力在2010—2020年間呈上升趨勢，雖然承載力有輕微的好轉，但是承載指數偏低，這種方法也可以很直觀地體現出武威市具體哪方面的水資源承載力較弱，從而更方便制定相應的改造計劃，對提升水資源承載力具有重要意義。

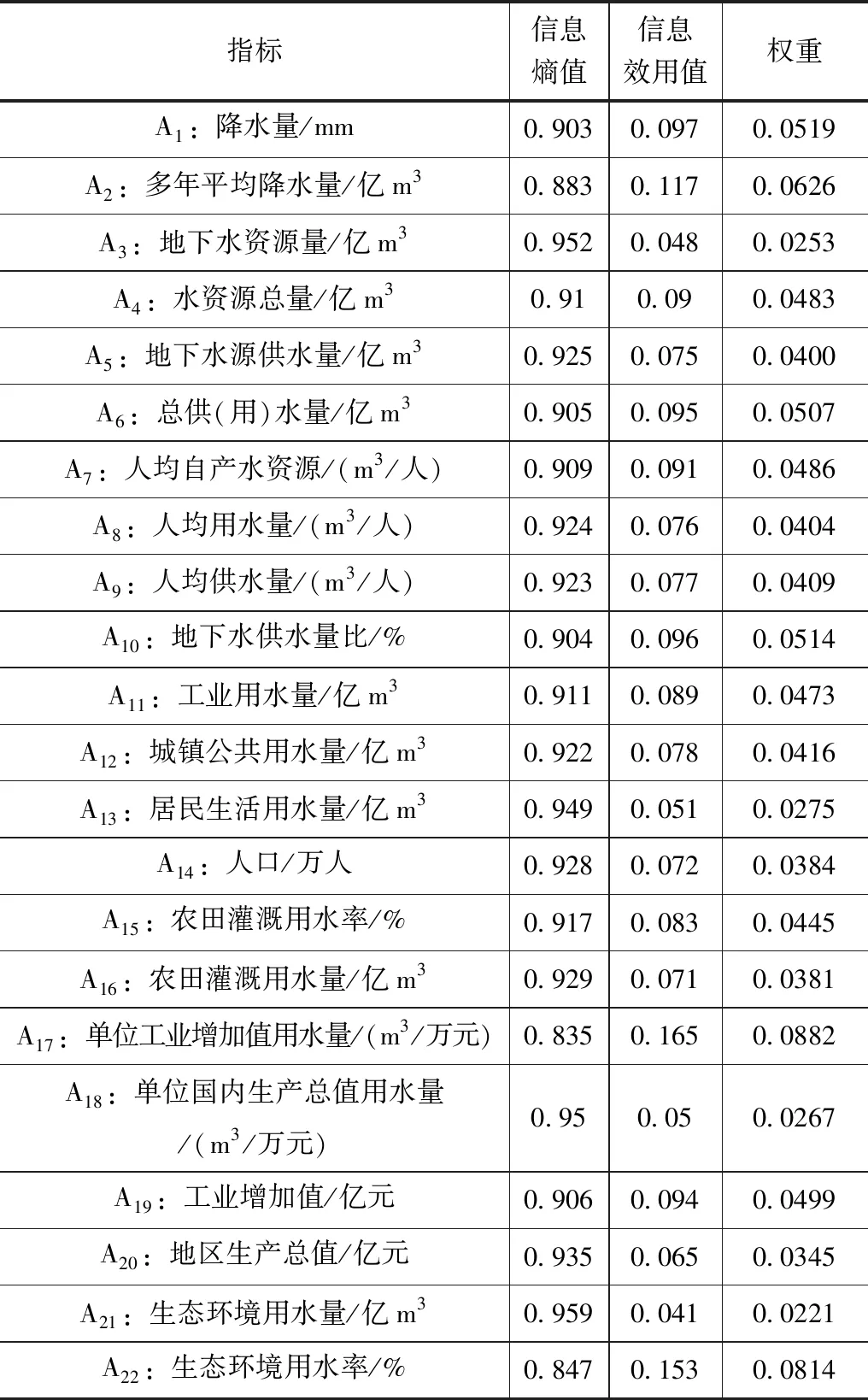
表2 熵權法結果表

3.2 基于模糊綜合法的承載力評價

從表3可以得出，武威市水資源承載力處于中等偏下的水平，在2010—2020年呈現波動增長的狀態，其中，承載力指數最大出現在2020年，最小出現在2013年，表明武威市水資源在近10年到達開發極限，水資源承載力處超載狀態。

3.3 基于TOPSIS模型的承載力評價

通過建立TOPSIS模型，對武威市水資源承載力進行了綜合評價，見表4。結果顯示，2010—2020年武威市水資源承載力處于超載狀態，2020年武威市水資源承載力指數達到最大，最小值出現在2015年，總體呈逐步上升的趨勢，如圖2所示。通過將模糊綜合評價結果與TOPSIS理論結果與許程程[7]、柳盼盼[10]、任曉燕等[12]、韓志文[25]的計算結果進行對比，計算結果基本符合武威市水資源現狀。

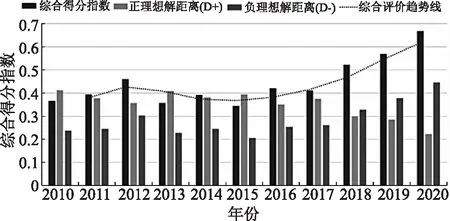
圖2 水資源承載力綜合評價趨勢

3.4 基于灰色預測模型的水資源承載力預測

將2種模型下的綜合評價值通過加權平均后得到預測值，將預測值代入灰色預測模型，得到武威市水資源承載力2021—2028年的預測結果，如圖3所示。由圖3可以看出，未來8年，武威市水資源承載力呈上升趨勢，且預測值與實際結果擬合情況良好，表明了預測結果符合武威市水資源承載力的現狀。結合各類指標對承載力的影響分析，武威市需將工作重點轉移向生態用水方面，并將工農業用水控制在合理的層面，可使水資源承載能力在2028年可達到臨界承載狀態。

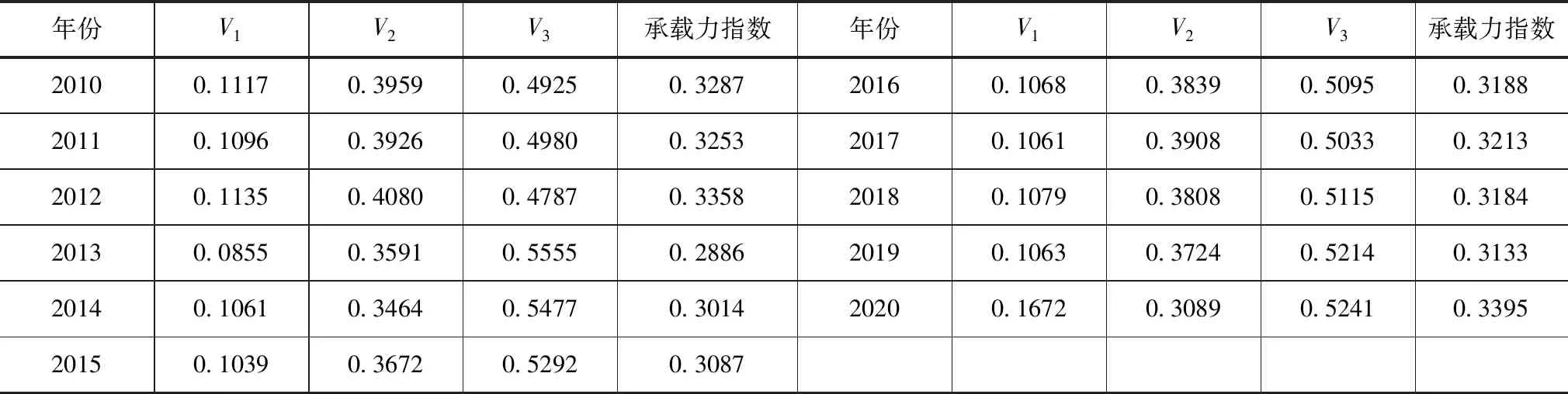
表3 模糊綜合評價指數

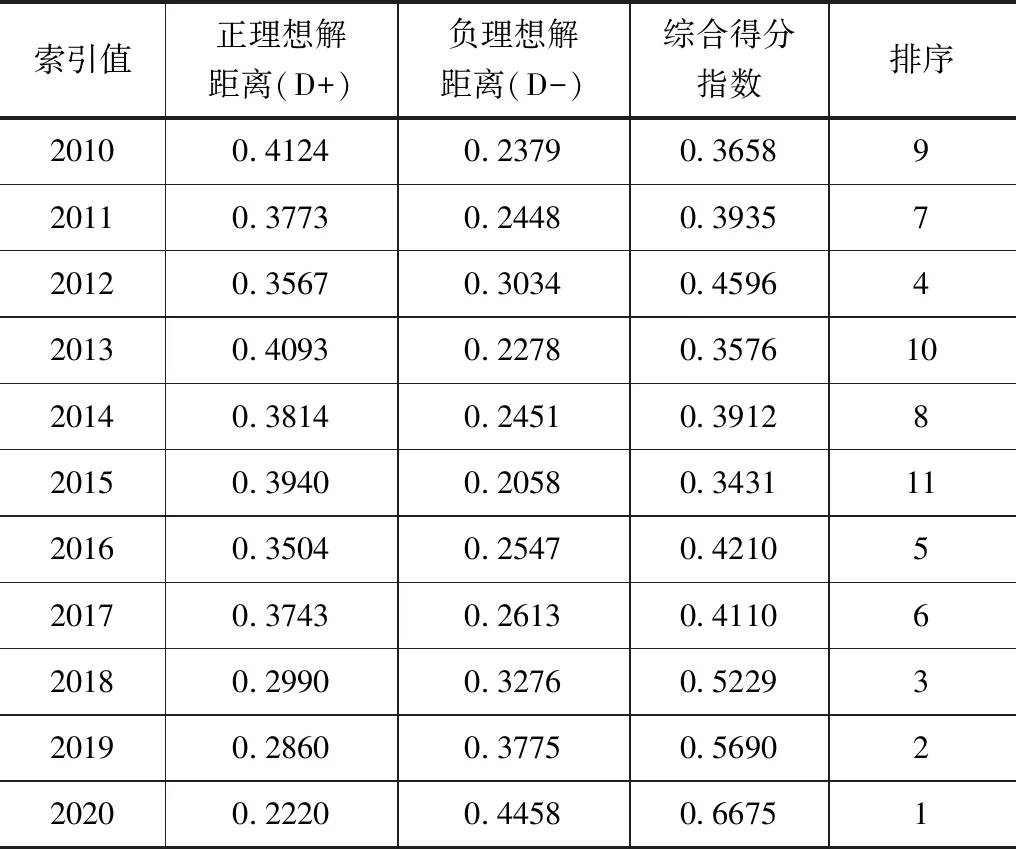
表4 武威市水資源承載力綜合評價結果

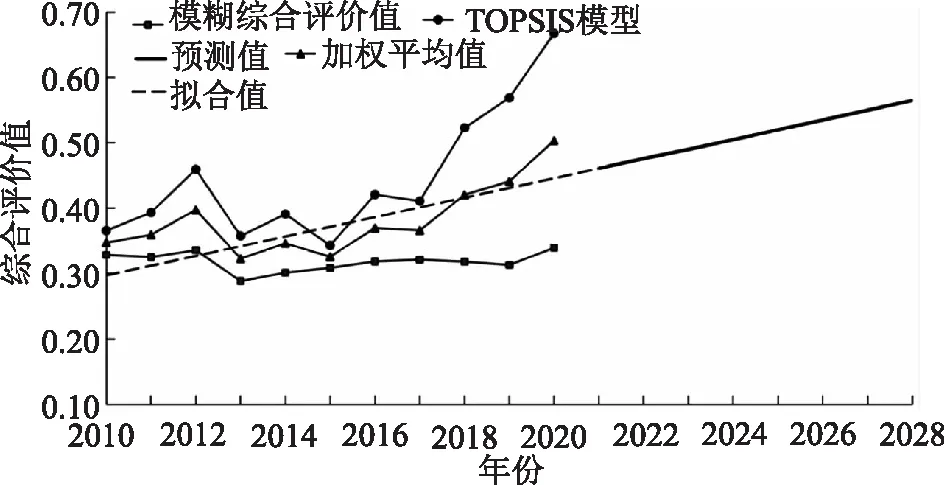
圖3 2010—2020武威市水資源承載力指數及未來8年預測指數

3.5 實測與預測的級比檢驗

通過運用GM(1，1)模型對殘差、相對誤差、級比偏差進行檢驗，結果見表5。結果顯示，模型相對誤差值最大值為15.989%，最小值為0，平均相對誤差為7.679%，小于10%，模型擬合效果達到較高標準。級比偏差均小于0.1，說明結果均達到了較高要求。原序列的所有年份的級比值都位于區間(0.846，1.181)內，適合構建灰色預測模型。

從以上分析可以看出，武威市水資源承載力在2010—2020年間呈上升趨勢。從總體看，武威市水資源承載力呈現超載狀態，原因是武威市水資源供給主要來源于地下水的開發利用，水資源補給來源于大氣降水以及祁連山的冰川融水，水資源需求量遠大于補給量。從評價方法來看，熵權法計算所得到的武威市各評價指標的權重與劉曉敏得出的結論相似[26]。模糊綜合評價法得出各年的評價數據結果差異不大。除2013年承載力指數處于0.3000以下，其他年份的承載力指數均高于0.3000，通過計算得出武威市這11年間的水資源承載力綜合平均值為0.3182；TOPSIS綜合評價法表明武威市在評價區間內的水資源承載力處于超載狀態，但逐年趨于好轉，具有很大的上升趨勢。同時，由于社會現代化加快，城鎮人口比重增加，武威市水資源壓力也逐日增加。供水和用水也極大增加了武威市水資源的壓力，由于科技條件的限制，使得農業用水效率和工業廢水排放量增加。武威市自身的地理條件，氣候干旱，降雨量少，增加了武威市地下水資源的壓力。水資源承載力指數最大值出現在2020年，較7年前最低的0.2886，高出了近十個百分點，說明在近幾年國家精準施策和地方政府的宏觀調控以及可持續發展觀念的深入，對武威市水資源承載力的增大有較明顯的效果。通過對未來8年的水資源承載力進行預測，武威市水資源承載力提升潛力巨大，在合理的規劃和利用下，2028年水資源承載能力可達到可承載狀態。

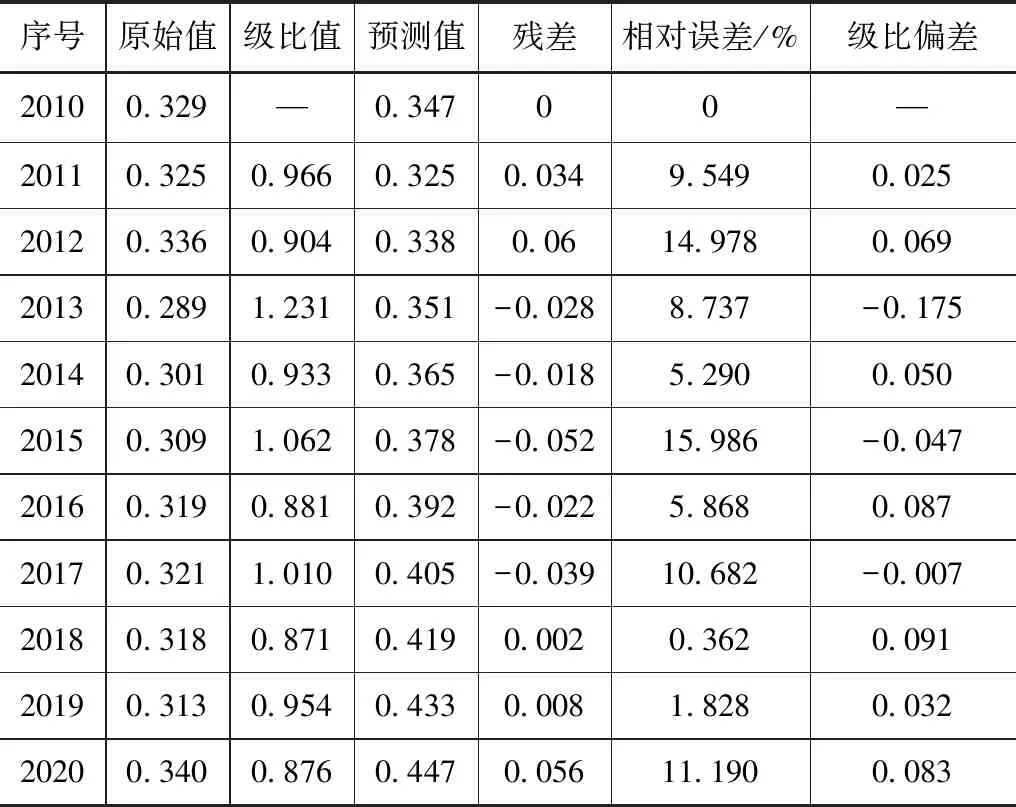
表5 級比檢驗結果

4 結論

文章對武威市水資源承載力進行了綜合分析，主要結論為：

(1)武威市2010—2020年武威市水資源承載力整體不容樂觀，綜合評價的平均值為0.3182，處于超載狀態，但承載能力具有較大的上升空間。

(2)武威市生態用水率和農業用水率較低，對水資源承載力影響較大。

(3)預測結果表明武威市水資源承載力呈上升趨勢，至2028年可達到臨界承載狀態。

評價結果可為武威市未來的水資源開發利用、生態環境的保護、社會經濟的發展提供參考依據。由于本文暫未收集武威市各流域水系的相關數據，導致評價指標構建不全面，下一步需利用大數據技術、GIS等手段獲取更全面的水資源數據，進一步完善評價指標體系。