車輛參數對車-橋耦合系統變截面連續梁橋損傷識別的影響

黃鵬飛,李雪峰,茆尚權

(1.合肥工業大學 土木與水利工程學院,安徽 合肥 230009;2.中建四局第六建設有限公司,安徽 合肥 230011)

近些年來,車-橋耦合振動理論取得較大發展,基于該理論的橋梁損傷識別方法也得到越來越多研究者的關注,與傳統的靜力損傷識別方法相比,這種動力損傷識別方法能夠取得更好的識別效果。文獻[1]通過對車輛加速度響應進行快速傅里葉變換,提取橋梁的一階頻率;文獻[2]提出需要消除環境因素的干擾,得到的結構頻率才會更精確;文獻[3]用短時頻域分解法處理車輛加速度響應,估算橋梁模態,通過數值案例可知,該方法對路面不平整度和噪聲因素比較敏感,需要結合其他方式進行橋梁損傷識別,如對橋施加外部激勵等;文獻[4]將損傷識別與遺傳算法相結合,通過車輛的加速度響應進行損傷定位與定量分析,并證明該方法在噪聲和路面不平順條件下也可以正常使用;文獻[5]將靈敏度分析方法用于橋上運動車輛加速度信號的分析處理中,再結合最小二乘法和正則化方法對橋梁結構進行損傷識別,結果表明，該方法在路面不平順和噪聲等級較高的情況下,損傷識別效果并不理想;文獻[6]對車輛的位移時程響應進行小波變換,數值算例表明,裂縫損傷程度越大越容易被識別,但對車速比較敏感;文獻[7]將模態應變能和遺傳算法相結合,提出一種多階段損傷檢測方法的理念,用車輛的振動響應成功實現兩跨連續梁橋的損傷位置和損傷程度識別;文獻[8]分析車輛懸架非線性和橋梁幾何非線性對連續梁橋耦合振動響應的影響,結果表明,兩者在一定程度上都能抑制橋梁的豎向跨中位移。

目前,橋梁損傷識別研究大多針對簡支梁和等截面連續梁等簡單橋梁結構,并且基本上都是從有限元軟件直接提取振動響應數據。本文基于有限分段思想將變截面連續梁分成j個梁段,j→∞時可以將各梁段視為等截面,從而建立1/4車輛模型和變截面連續梁橋的耦合振動方程,然后在MATLAB環境下編制基于Runge-Kutta算法的車-橋耦合振動數值分析程序,得到橋梁跨中的豎向位移,最后結合橋梁結構損傷前、后振型函數及自振頻率的變化,通過實際算例探討車橋質量比、車輛速度、車輛彈簧剛度及信噪比4組參數的變化對損傷識別的影響。

1 車-橋耦合振動方程建立

1.1 車輛模型建立

1/4車輛模型如圖1所示,將梁橋簡化成梁單元模型,車輛簡化為兩自由度的彈簧-阻尼系統。圖1中:mw為懸架和車輪的總質量;mv為車體質量;kw、cw分別為懸架體系的剛度和阻尼;kv、cv分別為車體的剛度和阻尼;yw、yv分別為懸架體系和車體的動撓度;y(x,t)為車輛作用點的動撓度。

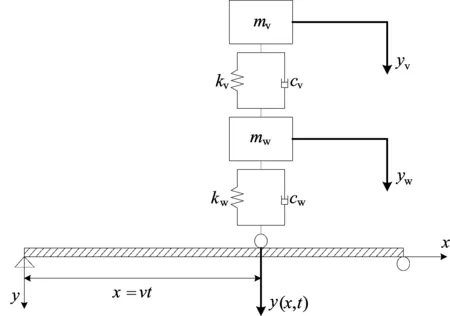
圖1 1/4車輛非線性模型

運用d’Alembert原理對懸架體系和車體進行受力分析。

1/4車輛模型的振動平衡方程用矩陣形式可表示為:

(1)

其中

1.2 橋梁模型建立

采用文獻[9]分析方法建立變截面連續梁橋的動力平衡方程,根據有限分段思想在梁軸線位置處取長度為dx的單元體進行研究,假定軸向壓應力FN為常值應力,且包含預應力V,其受力情況如圖2所示。

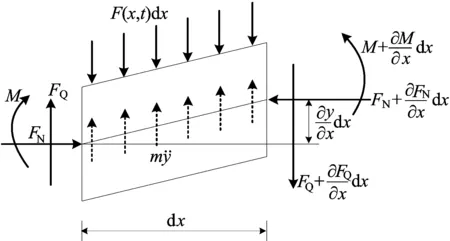
圖2 梁單元體計算模型

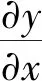
根據該單元體豎向力和力矩的平衡,可得:

(2)

(3)

設u(x,t)、y(x,t)分別為梁上荷載沿x、y方向的位移,由Euler-Bernoulli梁理論可得:

(4)

y(x,z,t)=y0(x,t)

(5)

其中:u0(x,t)、y0(x,t)分別為中性軸上任意位置的軸向位移和橫向位移;z為梁截面上某一點與中性軸的距離;t為時間。

混凝土梁的軸向應力較小,可忽略u0(x,t)的影響,根據梁的大位移小應變效應,其幾何非線性關系式為:

(6)

其中,ξx為距梁起點x處的軸向應變。

根據文獻[10]中Kelvin-Voigt模型,應力-應變本構關系為:

(7)

其中:σx為應力;E為梁的彈性模量;α為橋梁材料的黏性系數。

由σ-M關系式可得:

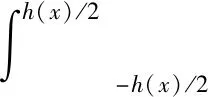
(8)

其中:b為截面寬度;h(x)為截面高度。

由σ-FN關系式可得:

(9)

聯立(6)～(9)式,代入(3)式求解,得到剪力FQ,對FQ求關于x的偏導后代入(2)式,可得:

(10)

1.3 車-橋耦合方程的建立與求解

令r(x)為橋面不平整度函數,x為車輛在橋上的位置,則車輛對橋的作用力P(t)、F(x,t)為:

P(t)=(mv+mw)g-kw[yw-y(x,t)-

(11)

F(x,t)=δ(x-vt)P(t)

(12)

其中:δ為Dirac函數;v為車輛行駛速度。將y(x,t)按照振型分解法分離變量后可得:

(13)

其中:Φi(x)、qi(t)分別為梁的第i階模態函數和模態坐標。

運用振型分解法進行求解,然后用伽遼金法進行化簡,整理后的結果聯立(3)式,可得變截面連續梁橋的車-橋耦合振動方程為:

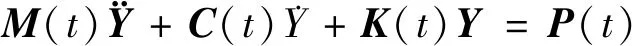
(14)

其中:M(t)為(N+2n)階廣義的車-橋耦合質量矩陣,N為橋梁振動方程所取階數,n為車輛數;C(t)為(N+2n)階廣義阻尼矩陣;K(t)為(N+2n)階廣義剛度矩陣;P(t)為(N+2n)階車-橋耦合作用外力向量;Y為(N+2n)階車-橋耦合位移向量。

(14)式為時變的二階非線性微分方程組,所取階數越大,計算精度越高,但工作量也相應變大,經試算可知,選取前3階振型可以兼顧精度和工作量。本文采用MATLAB編制基于Runge-Kutta算法的耦合振動模擬程序進行求解,模擬流程如圖3所示。

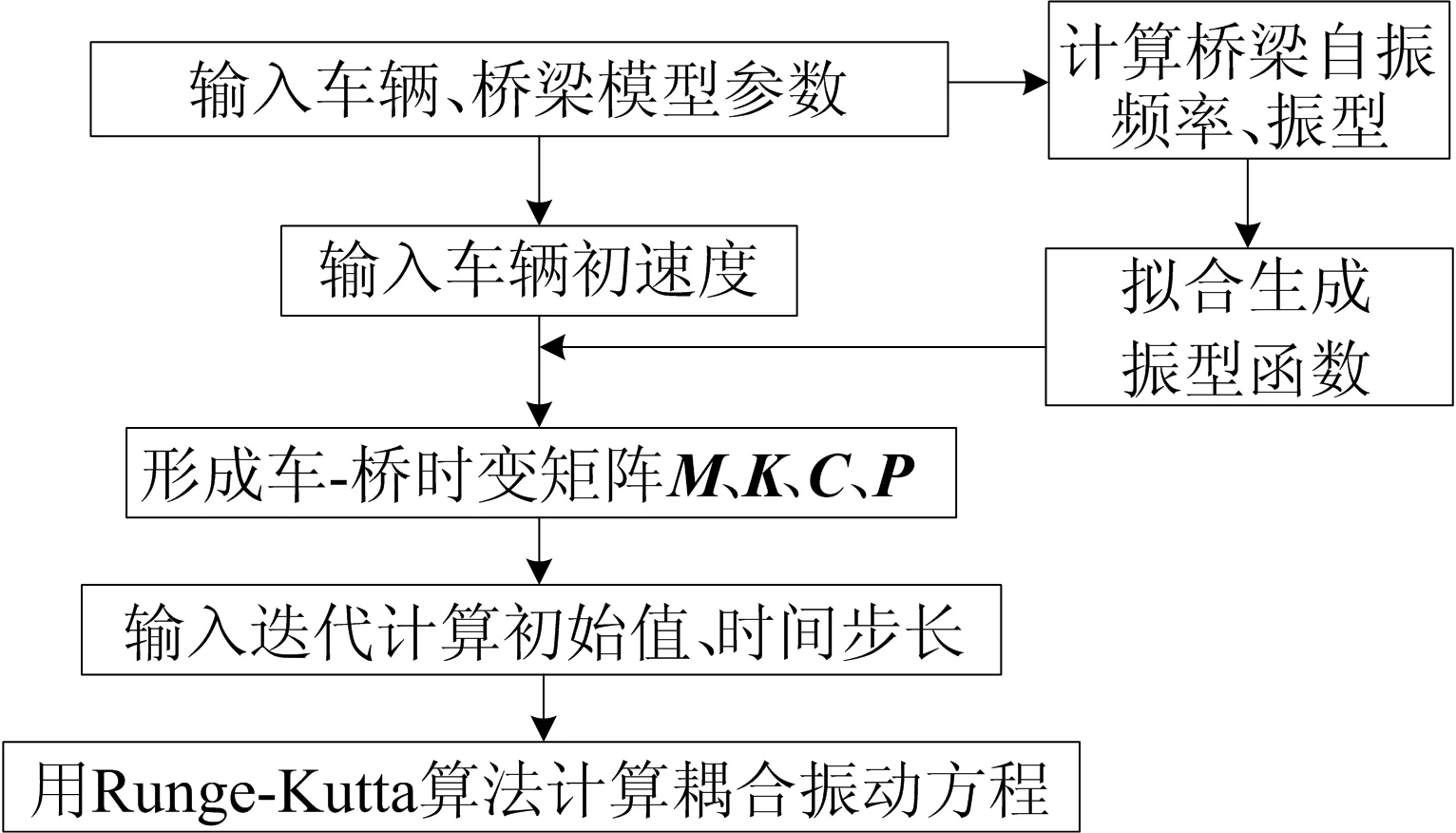
圖3 車-橋耦合振動模擬流程

2 車輛參數對橋梁損傷識別的影響

以某三跨混凝土連續梁橋為例。橋梁參數如下:橋梁跨徑為(27.92+42.00+27.92) m;梁體為C50混凝土,彈性模量E=34.5 GPa;混凝土密度ρ=2.5×103kg/m3,泊松比ν=0.2。箱梁跨中、支點處橫截面尺寸分別如圖4、圖5所示(單位為cm)。

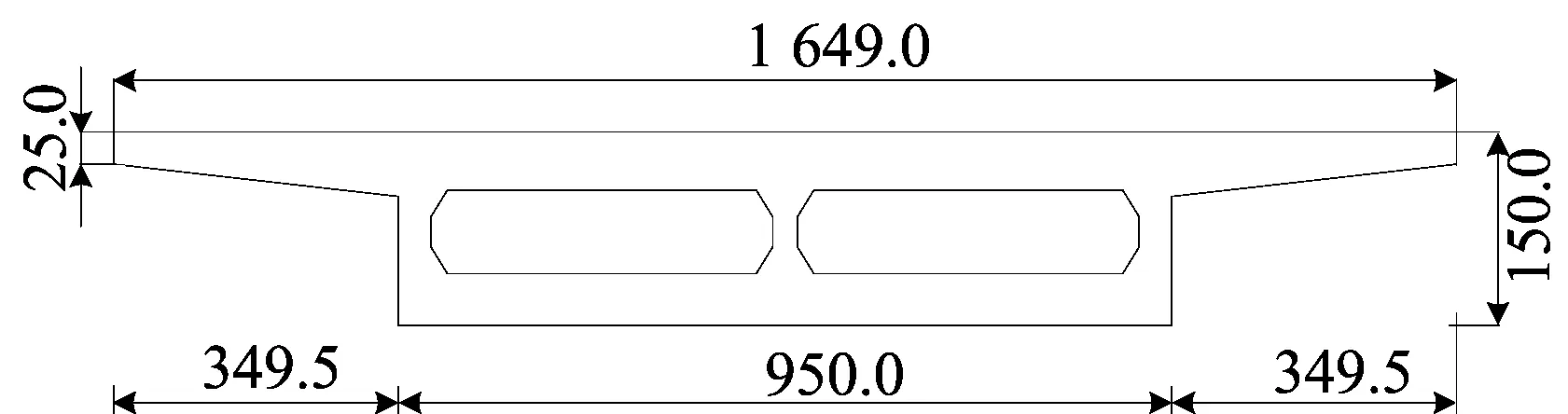
圖4 箱梁跨中橫截面

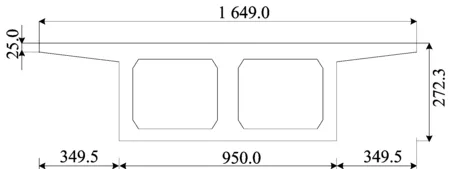
圖5 箱梁支點橫截面

車輛參數如下:車身質量mv=3.85×104kg;車身與懸架系統之間彈簧剛度kv=5.07 MN/m,阻尼cv=3.82×105kg/s;車輛懸架與車輪的總質量mw=8.66×103kg;車輛懸架與車輪系統彈簧剛度kw=8.56 MN/m,阻尼cw=1.96×105kg/s。

2.1 不同車橋質量比對橋梁損傷識別的影響

工況1 假定橋梁損傷位于中跨跨中附近位置,損傷程度取抗彎剛度折減40%,車輛移動速度設定為10 m/s,橋梁模型總質量為2 486.59 t,車輛模型總質量為10 t,車橋質量比為0.004,車輛其他參數不變,分別計算無損傷、中跨受損傷橋梁的跨中豎向位移響應,結果如圖6所示。

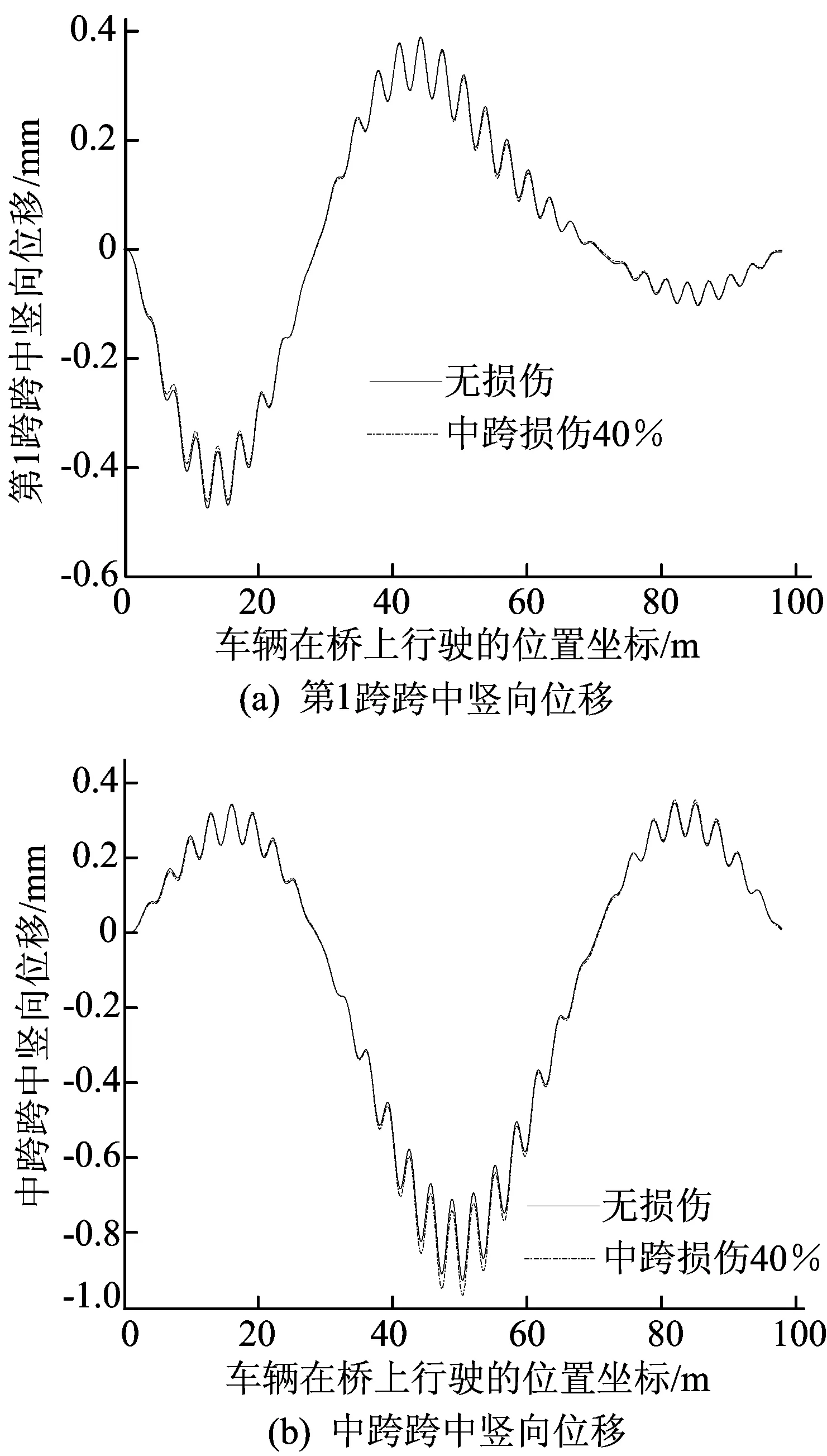
圖6 車橋質量比為0.004時無損傷、受損傷橋梁跨中豎向位移

由圖6可知,當車橋質量比為0.004時,無損傷、受損傷橋梁的跨中豎向位移響應曲線波動明顯,且十分相似,豎向位移響應曲線幾乎重合或基本一致,無法清晰識別出橋梁是否受到損傷。

工況2 車輛系統總質量增加到30 t,車橋質量比為0.012,其余參數同工況1,位移響應如圖7所示。

由圖7可知,車橋質量比提高為0.012,無損傷、受損傷橋梁的跨中豎向位移響應曲線波動明顯變弱,豎向位移響應曲線十分接近,但是跨中位移開始出現差異,在車輛行駛到橋梁受損傷位置處差異最為明顯。隨著車橋質量比增大,橋梁的第1跨跨中和中跨跨中的豎向位移響應也隨之變大,且數值變化程度十分明顯,其中無損傷、中跨受損傷橋梁的中跨跨中曲線第2峰峰值分別為-2.563、-2.670 mm,兩者相差0.107 mm。

工況3 車輛系統總質量提高到50 t,車橋質量比為0.020,其余參數同工況1,位移響應如圖8所示。

由圖8可知,車橋質量比達到0.020,橋梁跨中豎向位移響應曲線的波動繼續變弱,曲線更加平滑,無損傷、受損傷橋梁的第1跨跨中豎向位移響應曲線在橋梁局部位置開始出現微弱的偏差,橋梁的中跨跨中位移響應曲線出現明顯的差異,且響應數值進一步變大,無損傷、受損傷橋梁的中跨跨中曲線第2峰峰值分別為-4.201、-4.357 mm,兩者相差0.156 mm。

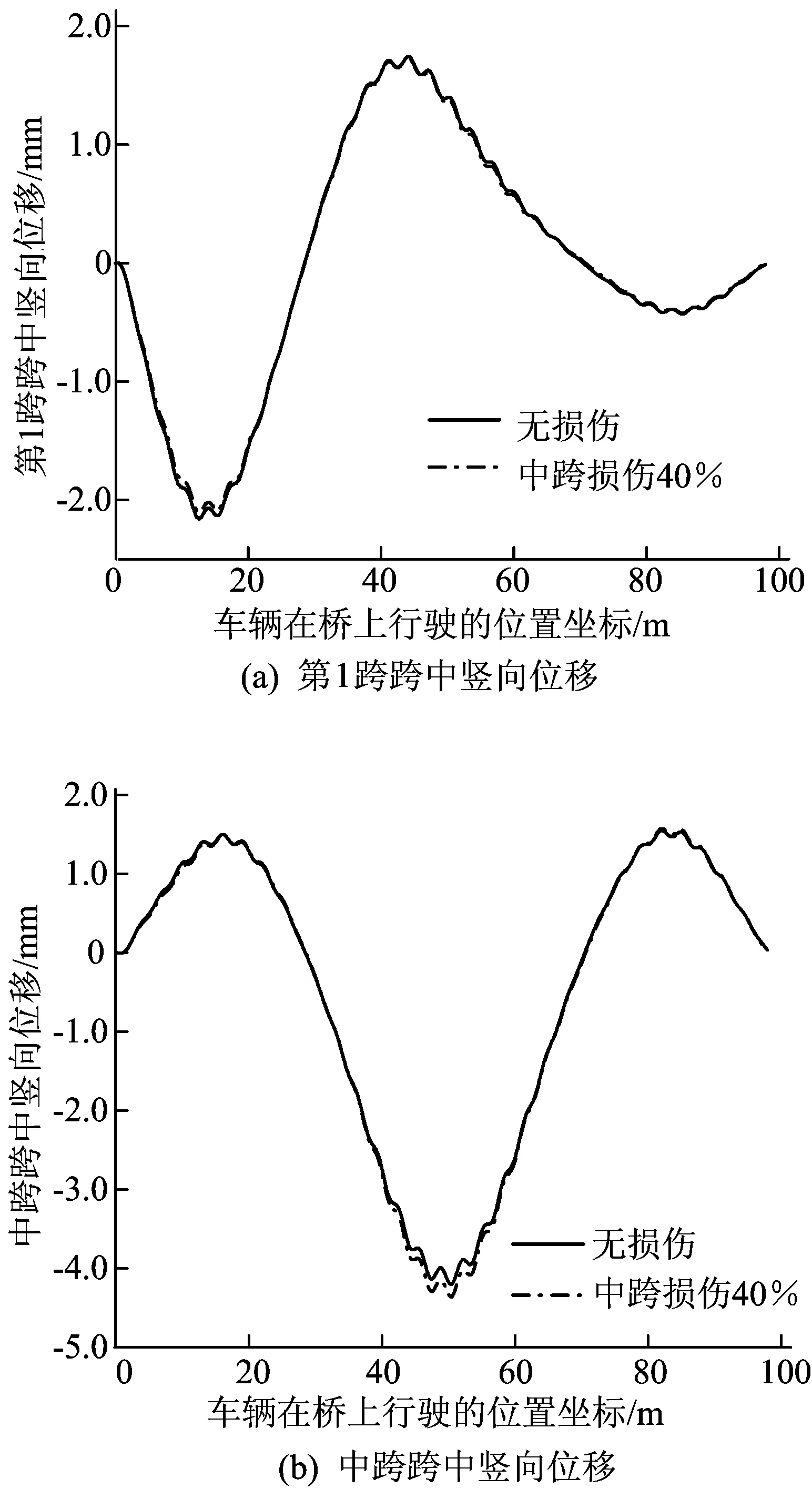
圖8 車橋質量比為0.020時無損傷、受損傷橋梁跨中豎向位移

由圖6～圖8可知,車橋質量比的改變對車-橋耦合振動損傷識別有影響,車橋質量比的不斷增大對橋梁跨中豎向位移響應曲線的整體趨勢沒有太大影響,無損傷橋梁和中跨受損傷橋梁是在幾乎相同位置達到曲線峰值,且曲線的波動不斷減弱,曲線的波動是由路面不平整因素引起的,由此可知,增大車橋質量比對路面不平整因素有抑制作用。隨著車橋質量比增加,橋梁跨中豎向位移數值增大,無損傷橋梁和中跨受損傷橋梁的中跨跨中豎向位移響應差值也增大,中跨受損傷橋梁更容易被識別。因此,在車-橋耦合振動識別變截面連續梁橋損傷研究中,應該選取車橋質量比大的車輛模型。

2.2 不同車速對橋梁損傷識別的影響

工況4 假定橋梁損傷位于中跨跨中附近位置,損傷程度取抗彎剛度折減40%,車輛模型總質量取初始參數47.16 t,車速10 m/s勻速駛過無損傷和中跨受損傷連續梁橋,其他參數不變,第1跨和中跨跨中豎向位移曲線如圖9所示。

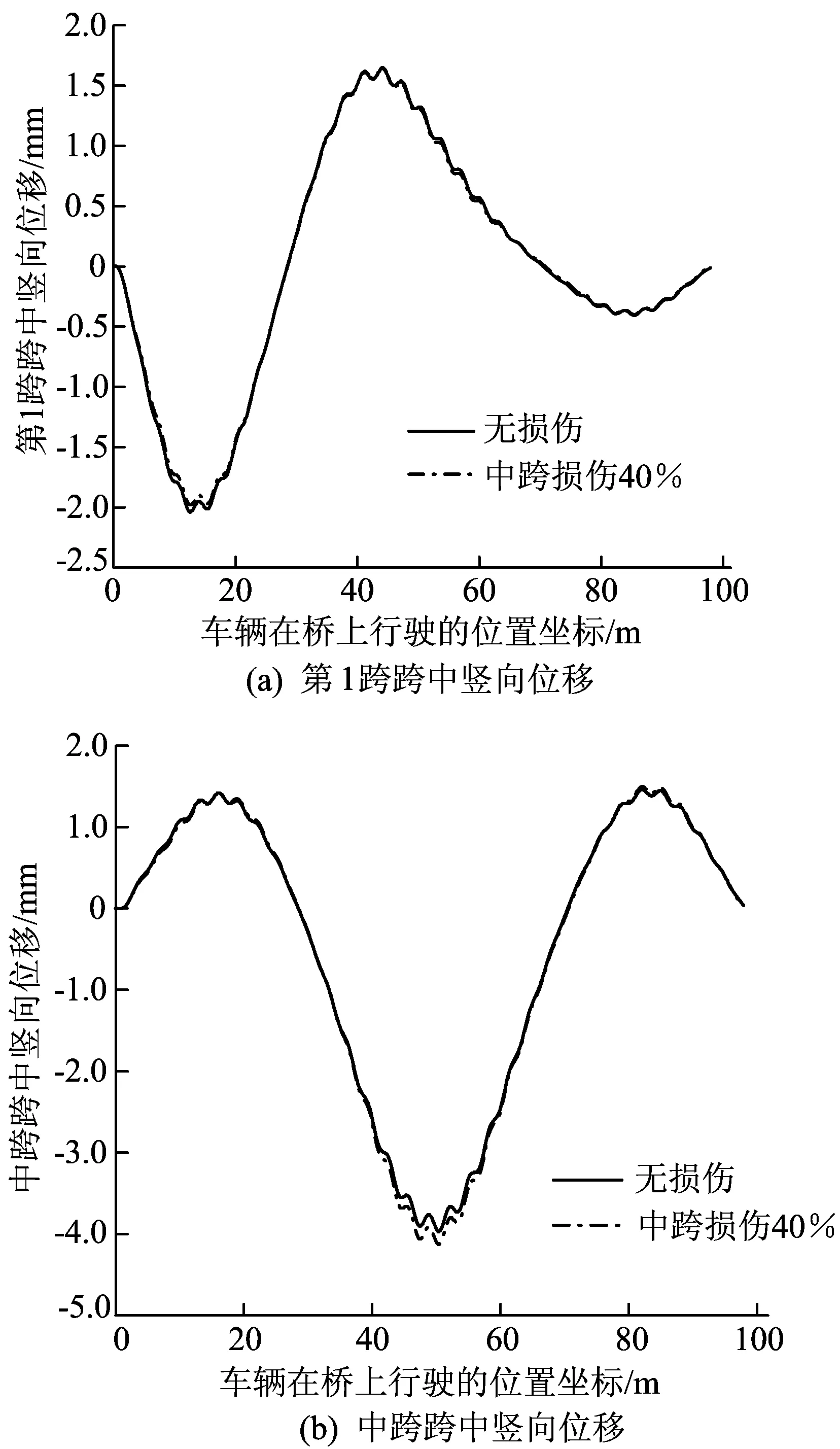
圖9 車速10 m/s時無損傷、受損傷橋梁跨中豎向位移

由圖9可知,車輛以10 m/s勻速通過橋梁時,無損傷、、中跨受損傷橋梁的第1跨跨中豎向位移響應、中跨跨中豎向位移響應的波動是一致的,都在相同的位置附近達到波峰、波谷。車輛分別在無損傷和中跨受損傷橋梁上行駛,行駛到第1跨跨中位置時,第1跨跨中豎向位移響應曲線有小幅的變化,但不是很明顯,此時中跨跨中豎向位移響應曲線幾乎沒有變化;車輛繼續行駛,當行駛到中跨跨中位置即損傷位置時,第1跨跨中豎向位移響應曲線很難觀察到區別,但是中跨跨中豎向位移響應曲線變化差異明顯,無損傷、受損傷橋梁中跨跨中曲線第2峰峰值分別為-3.968、-4.126 mm,兩者差值為0.158 mm。

工況5 提高車速至20 m/s,其余參數不變,豎向位移曲線如圖10所示。

由圖10可知,車輛以20 m/s勻速通過橋梁時,無損傷、受損傷橋梁的第1跨跨中豎向位移響應、中跨跨中豎向位移響應也具有相似的規律性,但和10 m/s勻速通過橋梁時的位移響應曲線有所區別,速度的提高使橋梁跨中豎向位移響應曲線的波動明顯變弱。車速的提高使得橋梁跨中豎向位移響應曲線峰值發生相應變化,無損傷、受損傷橋梁的中跨跨中曲線第2峰峰值分別為-4.001、-4.163 mm,兩者差值為0.162 mm。

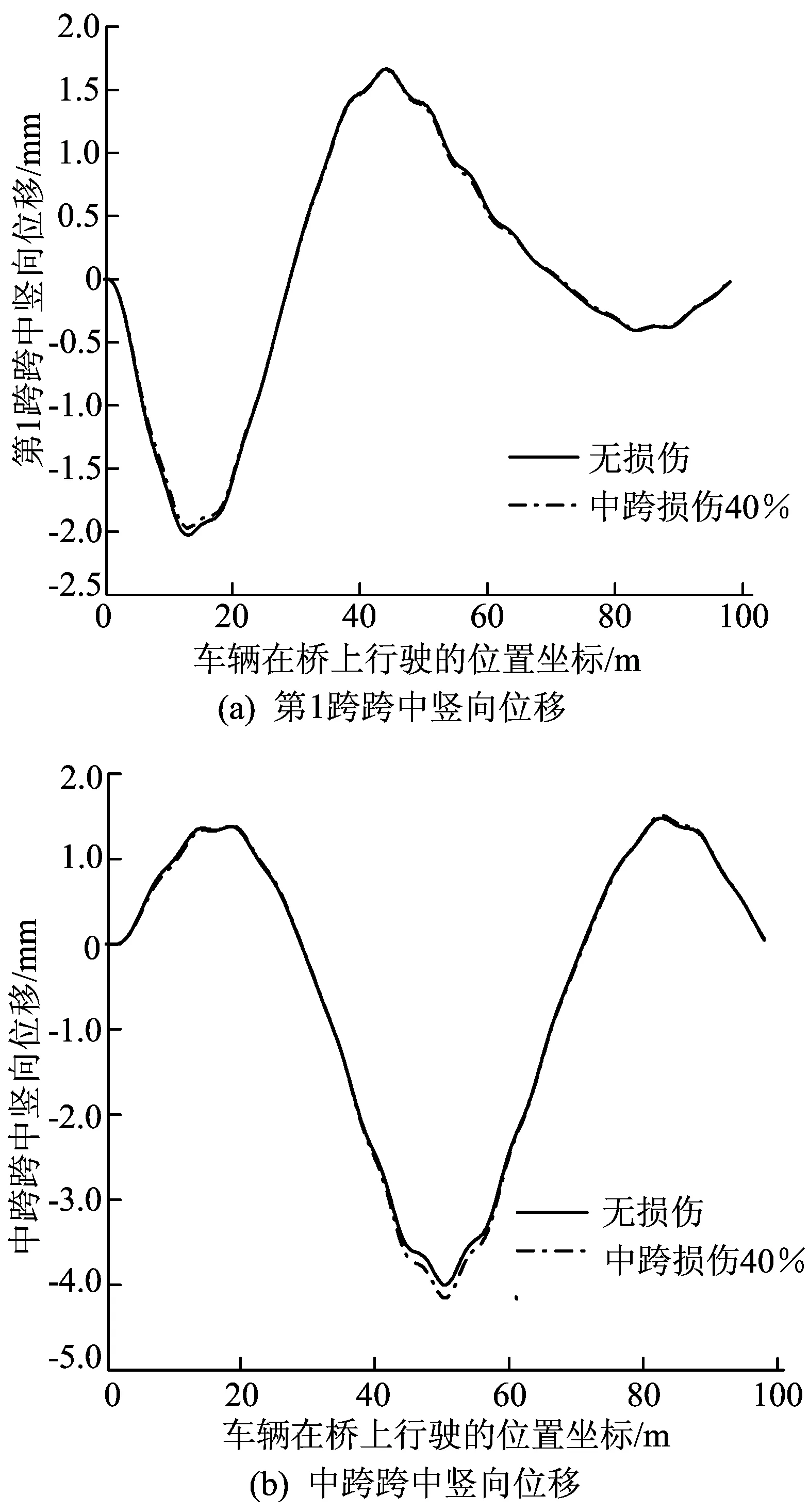
圖10 車速20 m/s時無損傷、受損傷橋梁跨中豎向位移

工況6 繼續提高車速至30 m/s,其余參數不變,豎向位移曲線如圖11所示。

由圖11可知,車輛以30 m/s勻速過橋,跨中豎向位移響應依然具有相似性,并且位移響應曲線波動繼續變弱。車速的提高使中跨跨中豎向位移響應曲線第2峰峰值的差值進一步擴大為0.185 mm,但是曲線峰值出現位置卻向橋頭方向移動,對車-橋耦合振動變截面連續梁橋損傷識別造成一定的干擾。

由圖9～圖11可知:車速的改變并沒有影響橋梁跨中豎向位移響應變化規律,豎向位移響應具有相似性,曲線的波峰、波谷位置十分接近。隨著車速不斷提高,中跨跨中豎向位移曲線第2峰峰值的差值不斷增大,但差值的增大幅度較小,車速10 m/s時差值為0.158 mm,車速30 m/s時差值為0.185 mm,僅相差0.027 mm,對橋梁損傷識別研究的影響不大;同時速度提高使橋梁跨中豎向位移響應曲線的波動性變弱,跨中豎向位移響應的峰值也向橋頭方向移動,對損傷識別研究造成一定的干擾。在實際試驗中,車輛行駛速度越快,外界的干擾越多,信號數據的采集越困難,會導致采集的數據不準確,因此在車-橋耦合振動識別變截面連續梁橋損傷后續研究中,采用行車速度為10 m/s。

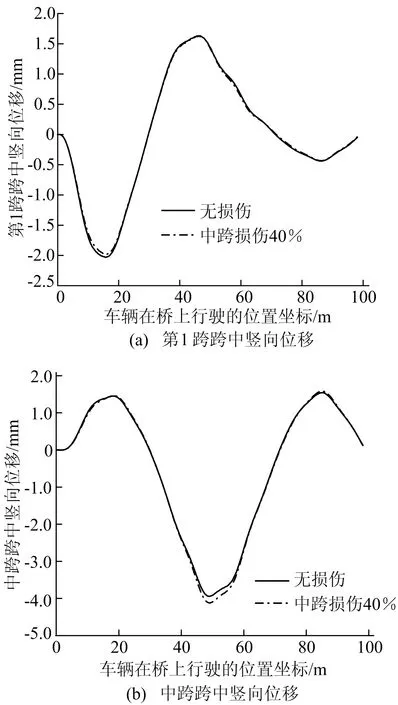
圖11 車速30 m/s時無損傷、受損傷橋梁跨中豎向位移

2.3 不同彈簧剛度對橋梁損傷識別的影響

工況7車身與懸架系統之間彈簧的剛度kv、車輛懸架與車輪系統彈簧的剛度kw取值均為500 kN/m,車速設定為10 m/s,其他參數不變,勻速駛過無損傷橋梁和受損傷橋梁,計算第1跨跨中和中跨跨中豎向位移響應曲線,結果如圖12所示。

由圖12可知,當車輛彈簧剛度為500 kN/m時,橋梁跨中豎向位移響應曲線的波動較微弱,曲線總體平滑,在局部位置有小幅振動。從圖12b可以看出,無損傷、受損傷橋梁曲線幾乎重合,僅在受損傷單元附近出現差異,兩者第2峰峰值分別為-3.917、-4.061 mm,兩者差值為0.144 mm。

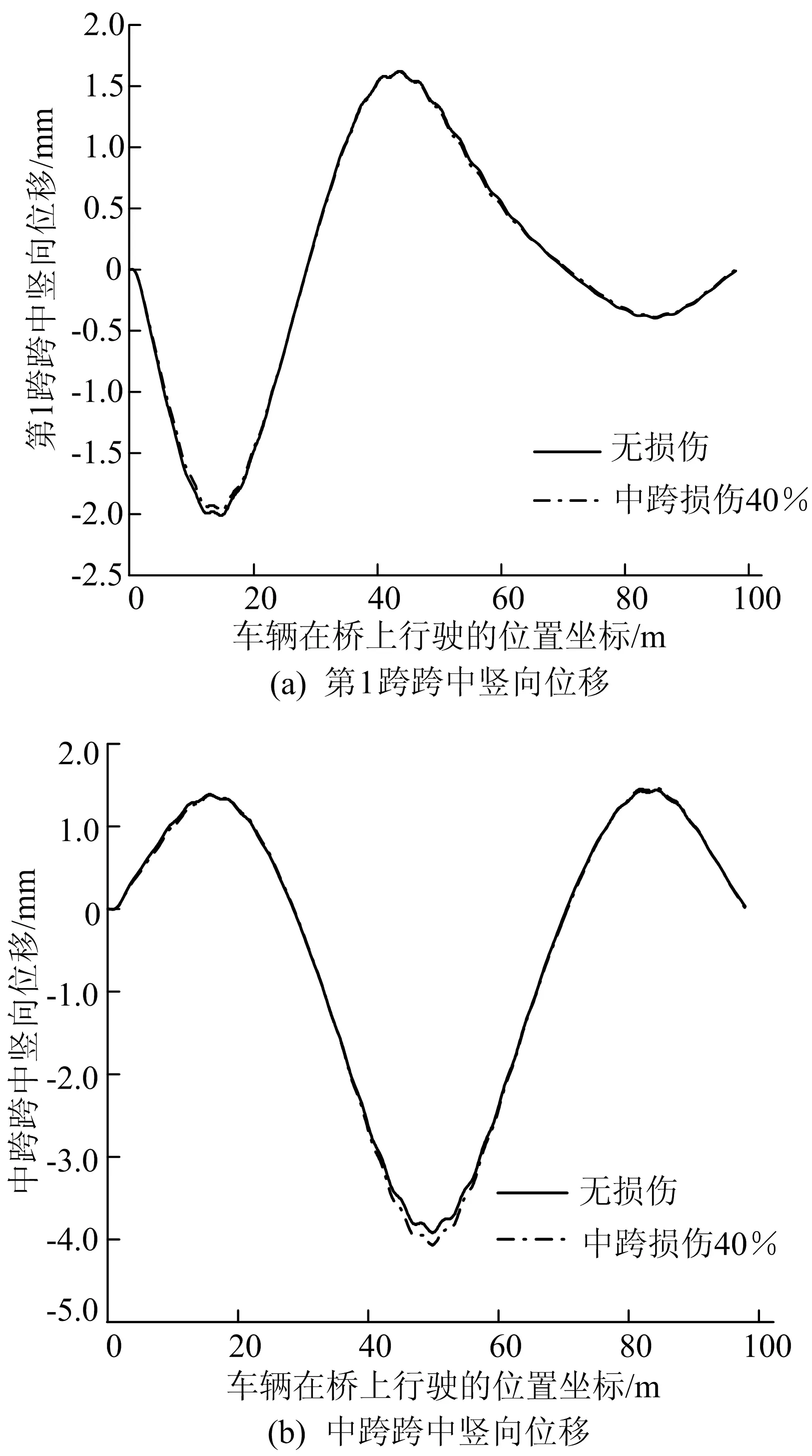
圖12 kv、kw為500 kN/m時無損傷、受損傷橋梁跨中豎向位移

工況8 車輛系統彈簧剛度為5 000 kN/m,其余參數同工況7,跨中豎向位移響應如圖13所示。由圖13可知,車輛系統彈簧剛度的增加使得橋梁跨中豎向位移響應曲線的波動稍變大,但沒有影響曲線整體的波動趨勢。由圖13b可知,無損傷、受損傷橋梁的曲線第2峰峰值依然存在差距,兩者分別為-3.936、-4.080 mm,兩者差值為0.144 mm,和工況7的差值一樣,沒有變化。

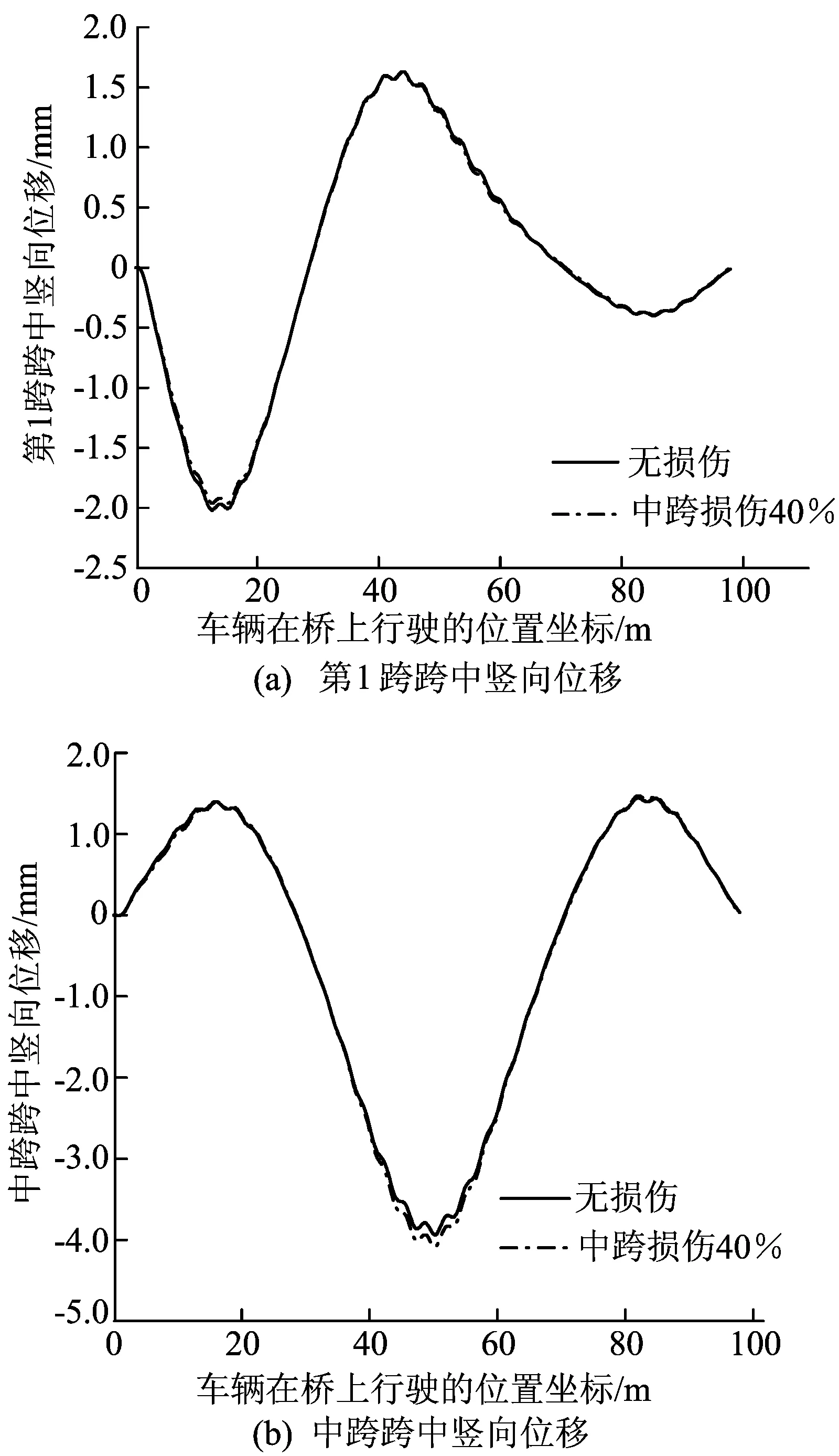
圖13 kv、kw為5 000 kN/m無損傷、受損傷橋梁跨中豎向位移

工況9 車輛系統彈簧剛度為50 000 kN/m,計算得到橋梁跨中豎向位移響應,如圖14所示。

從圖14可以看出，車輛系統彈簧剛度提高到50 000 kN/m后,橋梁跨中豎向位移響應曲線的波動性明顯增強,但2種情形的曲線幾乎重合,無明顯差異,很難進行損傷識別研究。

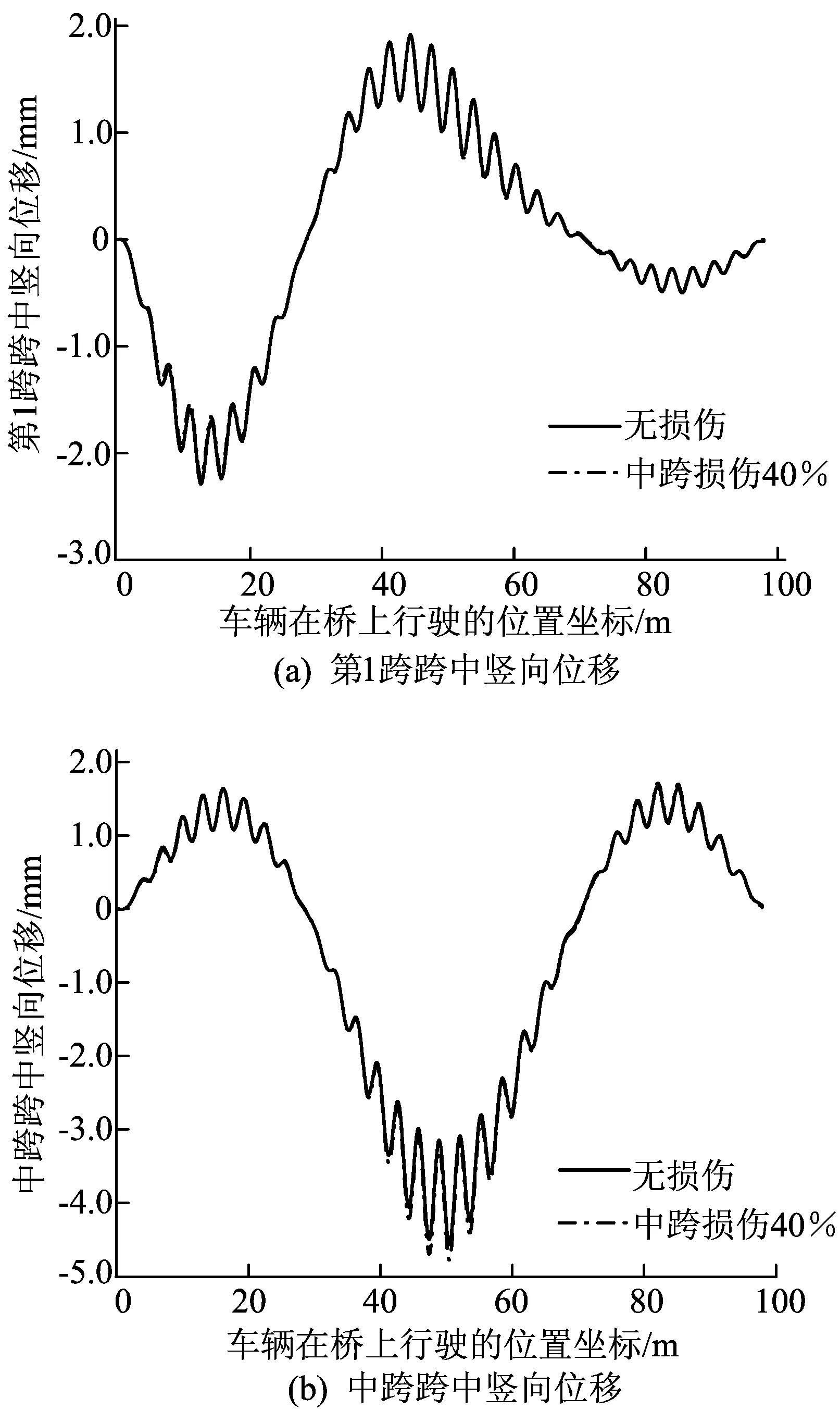
圖14 kv、kw為50 000 kN/m無損傷、受損傷橋梁跨中豎向位移

由圖12～圖14可知,改變車輛系統彈簧剛度后，橋梁跨中豎向位移曲線總體走向沒有改變,但是提高彈簧剛度使曲線波動性變得更加明顯,曲線的波動性與路面不平整度相關,可知車輛系統彈簧剛度的升高對路面不平整因素有放大作用。對比工況7和工況8,無損傷、受損傷橋梁中跨跨中豎向位移響應曲線第2峰峰值差值大小一樣,說明在一定范圍內,彈簧剛度參數對車-橋耦合振動識別橋梁損傷的影響很小,可以忽略不計。

2.4 不同信噪比對橋梁損傷識別的影響

車-橋耦合振動得到的位移響應存在噪聲的影響,因此在圖3流程中生成的位移響應部分加入不同信噪比下的高斯白噪聲,分析噪聲對橋梁損傷識別的影響。信噪比RSN計算公式為:

(15)

其中:y(i)為純信號序列;z(i)為高斯白噪聲序列;Q為項數;i為從1開始增大到Q的整數。

車輛模型總質量取初始參數47.16 t,車速取10 m/s,車輛系統彈簧剛度取500 kN/m,采樣頻率為100 Hz,信噪比取20、30、40 dB,剛度折減40%,計算無損傷、中跨受損傷橋梁的跨中豎向位移響應,結果如圖15所示。

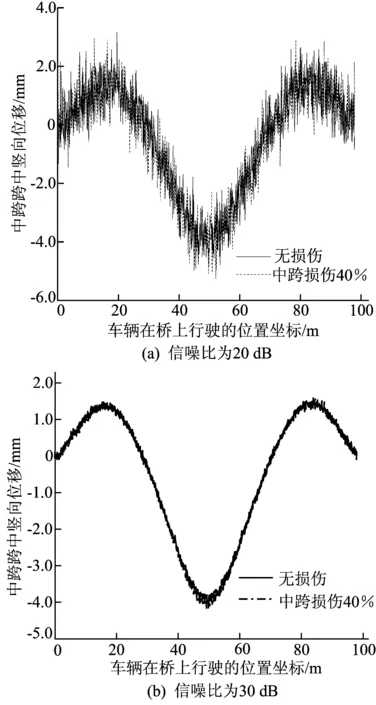
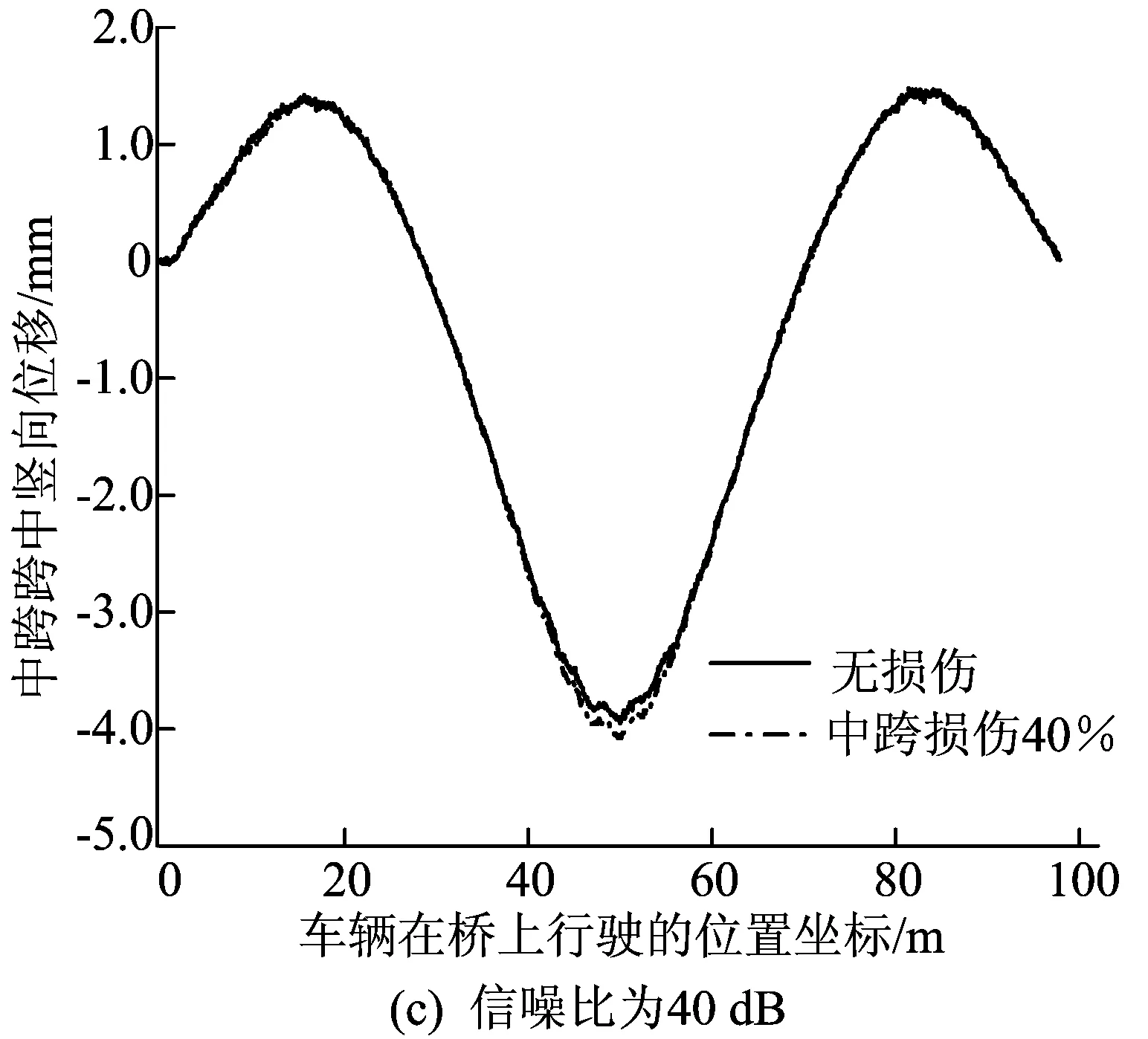
圖15 3種信噪比條件下無損傷、受損傷橋梁跨中豎向位移

由圖15可知:當信噪比為20 dB時,位移響應被噪聲所淹沒,信號完全失真;當信噪比增加到30 dB時,曲線的細節波動性明顯降低,無損傷、受損傷橋梁跨中位移開始出現差異,當車輛行駛到橋梁跨中受損傷位置時差異最為明顯,兩者峰值相差0.165 mm,比無噪聲時大0.021 mm,說明在一定情況下噪聲可以對位移響應產生影響;當信噪比進一步提高為40 dB時,曲線逐漸逼近圖12b中的無噪聲曲線,細節波動性進一步降低,無損傷、受損傷橋梁跨中位移差異更加明顯,2條曲線第2峰峰值分別為-3.994、-4.159 mm,兩者差值為0.136 mm,損傷識別效果比無噪聲時低0.008 mm,可以忽略不計。綜上可以看出,隨著信噪比提高,位移響應曲線逐漸逼近于無噪聲曲線,損傷識別效果也越來越好。

3 結 論

(1) 車橋質量比越大,對路面不平整因素的抑制作用越大,同時更加容易識別中跨受損傷橋梁與無損傷橋梁之間的區別,因此建議使用較重的車型進行車-橋耦合振動橋梁損傷識別研究。

(2) 車輛速度的提高會減弱橋梁跨中豎向位移響應曲線的波動性,同時跨中豎向位移響應的峰值不規律地向橋頭方向移動,對橋梁損傷識別研究有一定的干擾作用,因此建議使用較低的行車速度。

(3) 車輛模型中,彈簧剛度的大小和路面不平整因素之間有一定的聯系,但是對車-橋耦合振動橋梁損傷識別影響不大,可忽略此因素的影響。

(4) 信噪比較低時損傷識別效果較差,甚至完全被噪聲淹沒,但隨著信噪比提高,位移響應曲線逐漸逼近于無噪聲曲線,損傷識別效果也越來越好。基于車-橋耦合振動理論得到的位移響應信噪比較高,因此本文的方法具有實際意義,后續需要加強降噪研究。